部编新人教版小学六年级数学下册《圆柱的表面积》一课一练(带答案)
文档属性
| 名称 | 部编新人教版小学六年级数学下册《圆柱的表面积》一课一练(带答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 484.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 00:00:00 | ||
图片预览

文档简介
圆柱的表面积
第1关 练速度
1.填一填
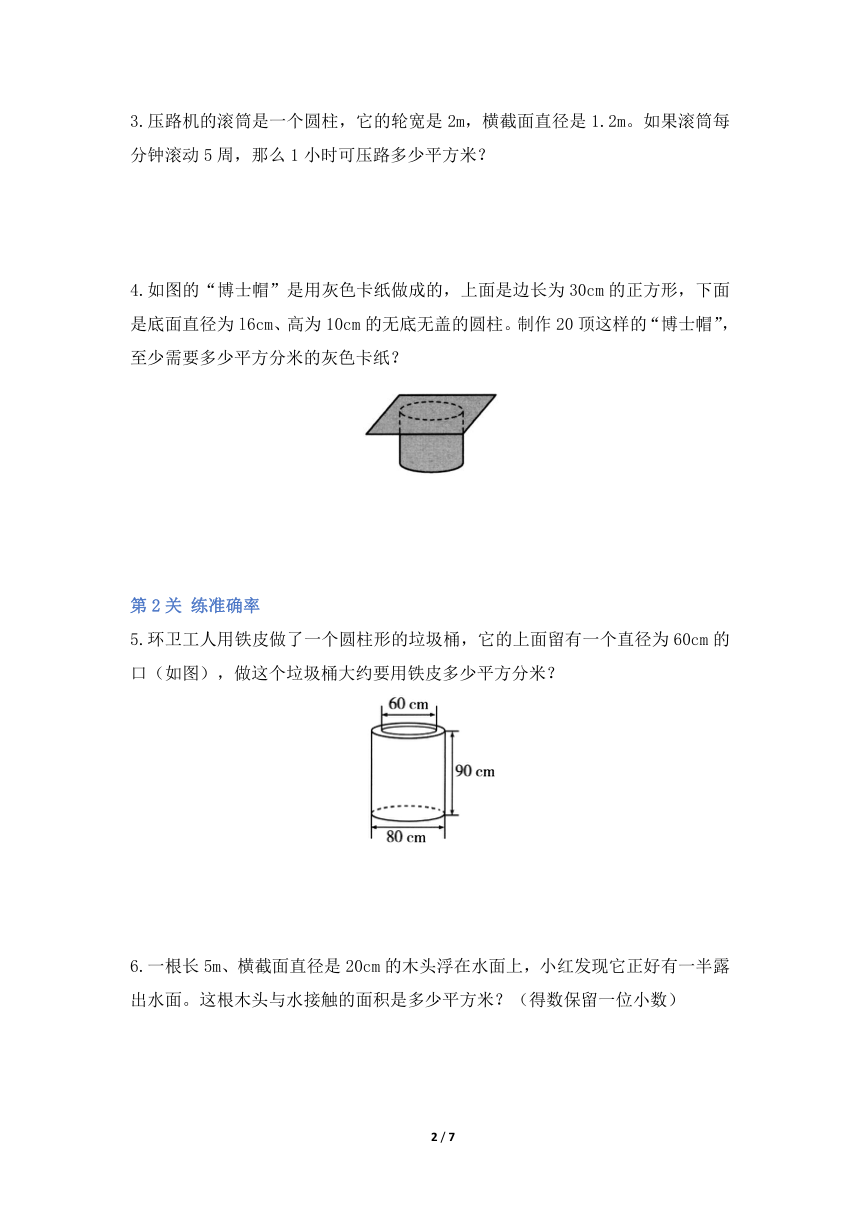
(1)下面是圆柱的展开图。
①A和B之间的距离是圆柱的( ),AB=( )cm;
②圆柱的侧面积是( )cm ;
③圆柱的表面积是( )cm 。
(2)填表。
底面半径(m) 底面直径(m) 高(m) 侧面积(m ) 表面积(m )
2.5 6
2 8
4 50.24
(3)一节圆柱形铁皮烟囱的长是1.5m,底面直径是0.2m,做100节这样的烟囱,至少需要( )m 的铁皮。
(4)一个圆柱的侧面积是314cm ,高是10cm,它的底面积是( )cm ,表面积是( )cm 。
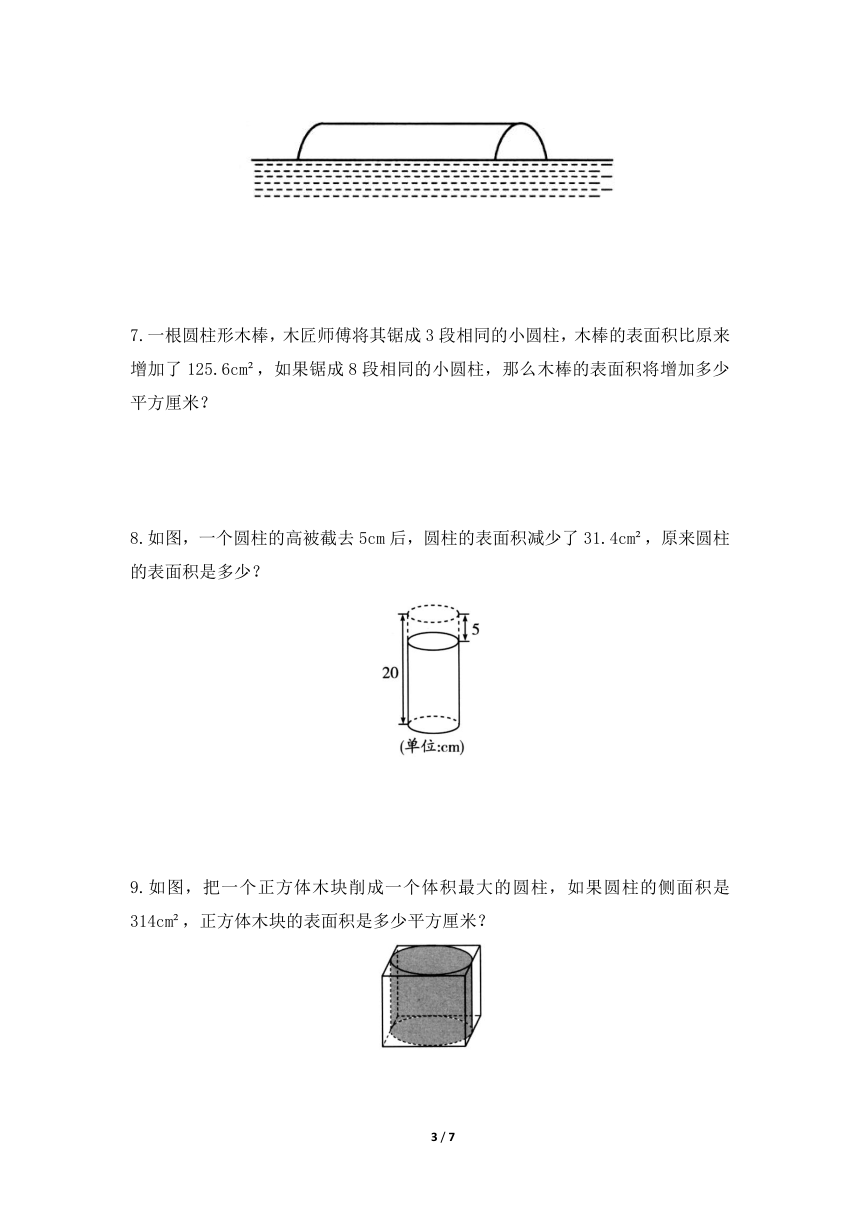
2.如图,给两个圆柱形水池的内壁和底面抹上水泥,抹水泥部分的面积一共是多少平方米?
3.压路机的滚筒是一个圆柱,它的轮宽是2m,横截面直径是1.2m。如果滚筒每分钟滚动5周,那么1小时可压路多少平方米?
4.如图的“博士帽”是用灰色卡纸做成的,上面是边长为30cm的正方形,下面是底面直径为l6cm、高为10cm的无底无盖的圆柱。制作20顶这样的“博士帽”,至少需要多少平方分米的灰色卡纸?
第2关 练准确率
5.环卫工人用铁皮做了一个圆柱形的垃圾桶,它的上面留有一个直径为60cm的口(如图),做这个垃圾桶大约要用铁皮多少平方分米?
6.一根长5m、横截面直径是20cm的木头浮在水面上,小红发现它正好有一半露出水面。这根木头与水接触的面积是多少平方米?(得数保留一位小数)
7.一根圆柱形木棒,木匠师傅将其锯成3段相同的小圆柱,木棒的表面积比原来增加了125.6cm ,如果锯成8段相同的小圆柱,那么木棒的表面积将增加多少平方厘米?
8.如图,一个圆柱的高被截去5cm后,圆柱的表面积减少了31.4cm ,原来圆柱的表面积是多少?
9.如图,把一个正方体木块削成一个体积最大的圆柱,如果圆柱的侧面积是314cm ,正方体木块的表面积是多少平方厘米?
10.有一张长方形铁皮,如图,剪下阴影部分围成一个圆柱,求这个圆柱的表面积。
第3关 练思维
11.长10cm,直径为2cm的两根圆柱捆成一捆(如图),用一张纸将这捆圆柱侧面包起来(纸要绷紧),至少需要多大面积的纸?
12.一段圆柱形木料,如果截成两个小圆柱,它的表面积将增加157cm ;如果沿着底面直径截成两个半圆柱,它的表面积将增加300cm 。求原来圆柱的表面积。
13.一段圆柱形钢材,底面直径是8dm、高是6dm,在它的上面正中间向下凿一个底面直径是4dm、高是2dm的小洞,接着在小洞的底面再向下凿一个底面直径是2dm、高是2dm的小洞,再接着在第2个小洞的底面向下凿一个底面直径是1dm、高是2dm的小洞(下底面被凿穿),现在这个立体图形的表面积是多少平方分米?
参考答案:
1.(1)①底面周长 18.84 ②113.04 ③169.56
(2)5 94.2 133.45 150.24 56.52 2 4 75.36
(3)94.2
(4)78.5 471
2.[3.14×6×1.5+3.14×() ]×2=113.04(m )
3.3.14×1.2×2×5×60=2260.8(m )
4.30×30+3.14×16×10=1402.4(cm ) 1402.4×20=28048(cm )
28048cm =280.48dm
提示:根据正方形的面积公式S=a2圆柱的侧面积公式S=Ch,把数据代入公式,先求出制作一顶“博士帽”需要的灰色卡纸的面积,然后乘20即可。
5.3.14×80×90+3.14×() ×2-3.14×() =29830(cm )
29830cm =298.3dm
提示:求做这个垃圾桶需要多少铁皮,就是求这个垃圾桶的表面积减去上面口的面积。
6.20cm=0.2m 3.14×(0.2÷2) +3.14×0.2×5÷2≈1.6(m )
提示:这根木头与水接触的面积等于一个圆的面积(两个半圆拼起来)与圆柱侧面积的一半的和。
7.125.6÷[(3-1)×2]×[(8-1)×2]=439.6(cm )
提示:把一根木棒锯成3段,需锯2次,锯成8段,需锯7次,每锯一次表面积增加两个底面的面积。
8.31.4÷5=6.28(cm) 6.28÷3.14÷2=1(cm)
3.14×1×2×20+3.14×1 ×2=131.88(cm )
提示:从图中可以看出,把圆柱的高截去5cm后,圆柱的表面积减少的其实是高为5cm的圆柱的侧面积,这样可根据侧面积公式用31.4÷5÷3.14÷2,求出原圆柱的底面半径,进而可求出圆柱的表面积。
9.314÷3.14×6=600(cm )
提示:把一个正方体木块削成一个体积最大的圆柱,则圆柱的底面直径和高都等于正方体的棱长。假设正方体的棱长为a,根据“圆柱的侧面积=底面周长×高”可得,π×a×a=314,由此可求出a 的值(正方体一个面的面积),最后再求出正方体的表面积。
10.18.84÷3.14÷2=3(cm)
3.14×3 ×2+18.84×(10-3×2)=131.88(cm )
提示:由题意和圆知阴影部分长方形的长是圆柱的底面周长,为18.84cm,由圆柱底面周长可求出底面面积。
11.3.14×2+2×2=10.28(厘米) 10.28×10=102.8(平方厘米)
提示:从底面看,纸的一边长是圆的周长加两个直径,一边长等于高。
12.157+300÷2×3.14=628(cm )
提示:把圆柱截成两个小圆柱,会增加两个底面,因此157cm 是两个底面面积之和;如果沿着底面直径截成两个半圆柱,将增加两个长方形,即其中个长方形的面积为300÷2=150(cm ),而这个长方形的面积=底面直径×高,圆柱的侧面积=底面周长×高=圆周率×底面直径×高,进而求出圆柱的侧面积。然后用两个底面积的和加上侧面积,就能求出该圆柱形木料的表面积。
13.3.14×(8÷2) ×2+3.14×8×6+3.14×(4+2+1)×2-3.141×(1÷2) ×2=293.59(dm )
提示:将挖洞后里面朝上的面向上平移,拼在一起,这就相当于把原来圆柱的上底面补全了一部分,上底面所剩的小洞直径是1分米。要求现在这个立体图形的表面积,需要用原来圆柱的表面积加上挖洞后增加的三个小圆柱的侧面积减去最小的洞的两个底面积。
1 / 7
第1关 练速度
1.填一填
(1)下面是圆柱的展开图。
①A和B之间的距离是圆柱的( ),AB=( )cm;
②圆柱的侧面积是( )cm ;
③圆柱的表面积是( )cm 。
(2)填表。
底面半径(m) 底面直径(m) 高(m) 侧面积(m ) 表面积(m )
2.5 6
2 8
4 50.24
(3)一节圆柱形铁皮烟囱的长是1.5m,底面直径是0.2m,做100节这样的烟囱,至少需要( )m 的铁皮。
(4)一个圆柱的侧面积是314cm ,高是10cm,它的底面积是( )cm ,表面积是( )cm 。
2.如图,给两个圆柱形水池的内壁和底面抹上水泥,抹水泥部分的面积一共是多少平方米?
3.压路机的滚筒是一个圆柱,它的轮宽是2m,横截面直径是1.2m。如果滚筒每分钟滚动5周,那么1小时可压路多少平方米?
4.如图的“博士帽”是用灰色卡纸做成的,上面是边长为30cm的正方形,下面是底面直径为l6cm、高为10cm的无底无盖的圆柱。制作20顶这样的“博士帽”,至少需要多少平方分米的灰色卡纸?
第2关 练准确率
5.环卫工人用铁皮做了一个圆柱形的垃圾桶,它的上面留有一个直径为60cm的口(如图),做这个垃圾桶大约要用铁皮多少平方分米?
6.一根长5m、横截面直径是20cm的木头浮在水面上,小红发现它正好有一半露出水面。这根木头与水接触的面积是多少平方米?(得数保留一位小数)
7.一根圆柱形木棒,木匠师傅将其锯成3段相同的小圆柱,木棒的表面积比原来增加了125.6cm ,如果锯成8段相同的小圆柱,那么木棒的表面积将增加多少平方厘米?
8.如图,一个圆柱的高被截去5cm后,圆柱的表面积减少了31.4cm ,原来圆柱的表面积是多少?
9.如图,把一个正方体木块削成一个体积最大的圆柱,如果圆柱的侧面积是314cm ,正方体木块的表面积是多少平方厘米?
10.有一张长方形铁皮,如图,剪下阴影部分围成一个圆柱,求这个圆柱的表面积。
第3关 练思维
11.长10cm,直径为2cm的两根圆柱捆成一捆(如图),用一张纸将这捆圆柱侧面包起来(纸要绷紧),至少需要多大面积的纸?
12.一段圆柱形木料,如果截成两个小圆柱,它的表面积将增加157cm ;如果沿着底面直径截成两个半圆柱,它的表面积将增加300cm 。求原来圆柱的表面积。
13.一段圆柱形钢材,底面直径是8dm、高是6dm,在它的上面正中间向下凿一个底面直径是4dm、高是2dm的小洞,接着在小洞的底面再向下凿一个底面直径是2dm、高是2dm的小洞,再接着在第2个小洞的底面向下凿一个底面直径是1dm、高是2dm的小洞(下底面被凿穿),现在这个立体图形的表面积是多少平方分米?
参考答案:
1.(1)①底面周长 18.84 ②113.04 ③169.56
(2)5 94.2 133.45 150.24 56.52 2 4 75.36
(3)94.2
(4)78.5 471
2.[3.14×6×1.5+3.14×() ]×2=113.04(m )
3.3.14×1.2×2×5×60=2260.8(m )
4.30×30+3.14×16×10=1402.4(cm ) 1402.4×20=28048(cm )
28048cm =280.48dm
提示:根据正方形的面积公式S=a2圆柱的侧面积公式S=Ch,把数据代入公式,先求出制作一顶“博士帽”需要的灰色卡纸的面积,然后乘20即可。
5.3.14×80×90+3.14×() ×2-3.14×() =29830(cm )
29830cm =298.3dm
提示:求做这个垃圾桶需要多少铁皮,就是求这个垃圾桶的表面积减去上面口的面积。
6.20cm=0.2m 3.14×(0.2÷2) +3.14×0.2×5÷2≈1.6(m )
提示:这根木头与水接触的面积等于一个圆的面积(两个半圆拼起来)与圆柱侧面积的一半的和。
7.125.6÷[(3-1)×2]×[(8-1)×2]=439.6(cm )
提示:把一根木棒锯成3段,需锯2次,锯成8段,需锯7次,每锯一次表面积增加两个底面的面积。
8.31.4÷5=6.28(cm) 6.28÷3.14÷2=1(cm)
3.14×1×2×20+3.14×1 ×2=131.88(cm )
提示:从图中可以看出,把圆柱的高截去5cm后,圆柱的表面积减少的其实是高为5cm的圆柱的侧面积,这样可根据侧面积公式用31.4÷5÷3.14÷2,求出原圆柱的底面半径,进而可求出圆柱的表面积。
9.314÷3.14×6=600(cm )
提示:把一个正方体木块削成一个体积最大的圆柱,则圆柱的底面直径和高都等于正方体的棱长。假设正方体的棱长为a,根据“圆柱的侧面积=底面周长×高”可得,π×a×a=314,由此可求出a 的值(正方体一个面的面积),最后再求出正方体的表面积。
10.18.84÷3.14÷2=3(cm)
3.14×3 ×2+18.84×(10-3×2)=131.88(cm )
提示:由题意和圆知阴影部分长方形的长是圆柱的底面周长,为18.84cm,由圆柱底面周长可求出底面面积。
11.3.14×2+2×2=10.28(厘米) 10.28×10=102.8(平方厘米)
提示:从底面看,纸的一边长是圆的周长加两个直径,一边长等于高。
12.157+300÷2×3.14=628(cm )
提示:把圆柱截成两个小圆柱,会增加两个底面,因此157cm 是两个底面面积之和;如果沿着底面直径截成两个半圆柱,将增加两个长方形,即其中个长方形的面积为300÷2=150(cm ),而这个长方形的面积=底面直径×高,圆柱的侧面积=底面周长×高=圆周率×底面直径×高,进而求出圆柱的侧面积。然后用两个底面积的和加上侧面积,就能求出该圆柱形木料的表面积。
13.3.14×(8÷2) ×2+3.14×8×6+3.14×(4+2+1)×2-3.141×(1÷2) ×2=293.59(dm )
提示:将挖洞后里面朝上的面向上平移,拼在一起,这就相当于把原来圆柱的上底面补全了一部分,上底面所剩的小洞直径是1分米。要求现在这个立体图形的表面积,需要用原来圆柱的表面积加上挖洞后增加的三个小圆柱的侧面积减去最小的洞的两个底面积。
1 / 7
