6.6.3立体图形体积和表面积复习教案 六年级数学下册 青岛版
文档属性
| 名称 | 6.6.3立体图形体积和表面积复习教案 六年级数学下册 青岛版 |  | |
| 格式 | doc | ||
| 文件大小 | 645.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 18:29:19 | ||
图片预览

文档简介
6.6.3立体图形体积和表面积复习
一、复习目标
1、使学生在整理和复习各种平面、立体图形的特征、各种图形之间的联系的基础上,复习和整理立体图形的表面积和体积计算方法。
2、使学生能熟练的运用立体图形的表面积和体积计算公式解决实际问题。
3、掌握立体图形的表面积体积计算公式的推导过程,了解它们之间的联系。
二、课时安排:1课时
三、复习重难点:使学生能熟练的运用立体图形的表面积和体积计算公式解决实际问题。
四、教学过程
(一)知识梳理
同学们以前我们学过立体图形的表面积和体积计算方法,我们学过的立体图形的体积计算公式是怎样推导出来的?它们之间有怎样的联系?
回顾整理要求:
1. 小组合作,回忆立体图形和立体图形的知识;
2. 根据知识间的关系合理地整理;
3. 把整理的结果用表格、流程图、树状图等自己喜欢的方式表示出来。
(二)题型、方法归纳
1、生讨论交流:
我们学过哪些立体图形?
长方体 正方体 圆柱 圆锥
这些立体图形的体积计算公式,是怎样推导出来的?
(1)长方体体积的推导:
长方体的体积 = 长×宽×高 V = ɑbh
长方体的体积 = 底面积×高 V = Sh
(2)正方体体积的推导:
正方体是长、宽、高都相等的长方体。
正方体的体积 = 棱长×棱长×棱长 V = ɑ3
长方体的体积 = 底面积×高 V = Sh
(3)圆柱体体积的推导:
转化成长方体,圆柱的体积 = 底面积×高 V = S h
(4)圆锥体体积的推导:
实验、转化圆锥的体积是等底等高的圆柱体积的 。
圆锥的体积 = × 底面积×高
师生小结:
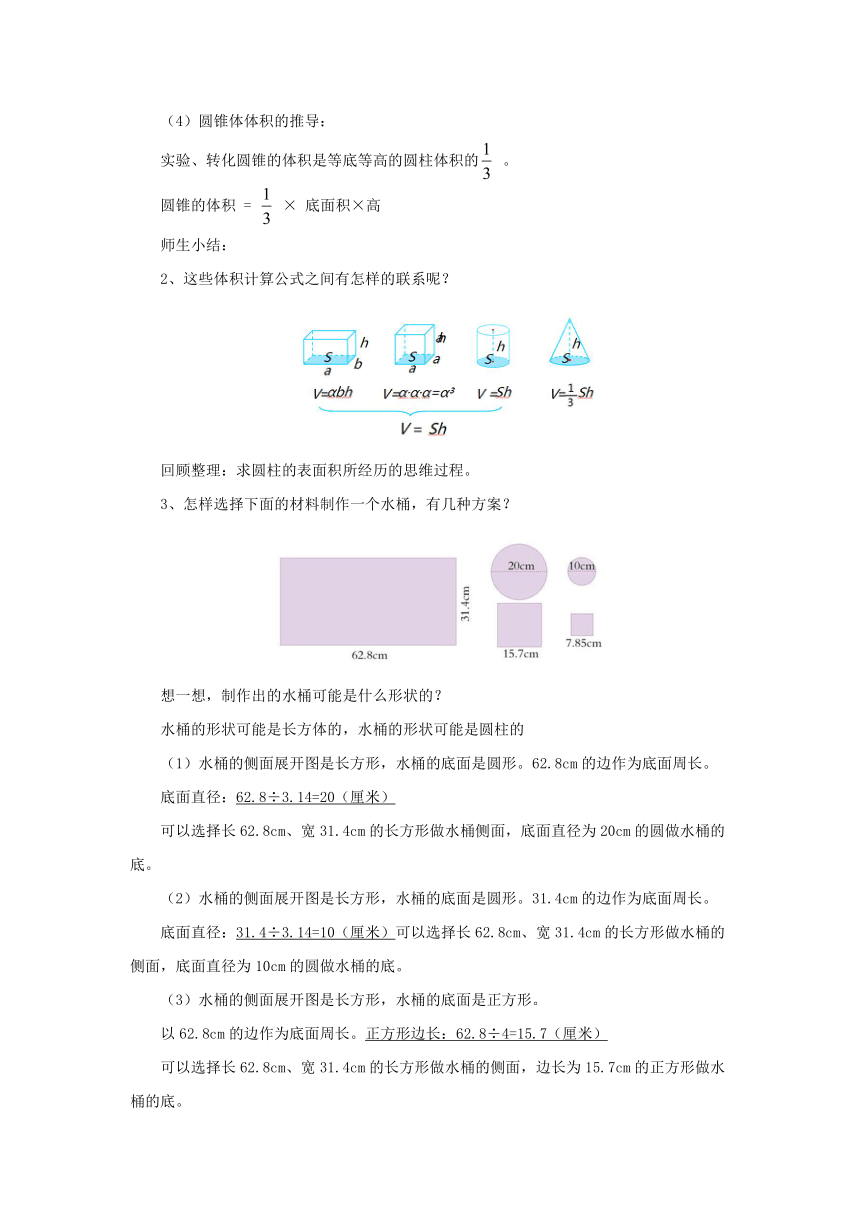
2、这些体积计算公式之间有怎样的联系呢?
回顾整理:求圆柱的表面积所经历的思维过程。
3、怎样选择下面的材料制作一个水桶,有几种方案?
想一想,制作出的水桶可能是什么形状的?
水桶的形状可能是长方体的,水桶的形状可能是圆柱的
(1)水桶的侧面展开图是长方形,水桶的底面是圆形。62.8cm的边作为底面周长。
底面直径:62.8÷3.14=20(厘米)
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,底面直径为20cm的圆做水桶的底。
(2)水桶的侧面展开图是长方形,水桶的底面是圆形。31.4cm的边作为底面周长。
底面直径:31.4÷3.14=10(厘米)可以选择长62.8cm、宽31.4cm的长方形做水桶的侧面,底面直径为10cm的圆做水桶的底。
(3)水桶的侧面展开图是长方形,水桶的底面是正方形。
以62.8cm的边作为底面周长。正方形边长:62.8÷4=15.7(厘米)
可以选择长62.8cm、宽31.4cm的长方形做水桶的侧面,边长为15.7cm的正方形做水桶的底。
(4)水桶的侧面展开图是长方形,水桶的底面是正方形. 长方形的宽等于底面周长
正方形边长:31.4÷4=7.85(厘米)可以选择长62.8cm、宽31.4cm的长方形做水桶的侧面,边长为7.5cm的正方形做水桶的底。
(三)典例精讲
我们是怎样用转化的方法推导出立体图形的体积计算公式的?
(四)归纳小结
(五)随堂检测
1、求立体图形的体积和表面积。(只列式不计算)
2、一个长方体苹果箱的规格是40×30×25(单位:m),它的体积是多少立方厘米?制作10个这样的纸箱至少需要多少板纸?
3、用下面的五块玻璃做一个鱼缸,这个鱼缸的底面积是多少?它能装多少升水?(玻璃的厚度不计)
4、一个正方体水箱,棱长是40厘米。如果将一个石块浸入水中,水面上升2厘米。这个石块的体积是多少?
5、瓶子里装着一些水(如下图所示),瓶底面积是0.8平方分米,请你想办法计算瓶子的容积。
五、板书设计
立体图形的体积和表面积
立体图形的体积推导
问题 想象 选择 计算 答案
立体 平面 立体
不规则图形转化成规则物体
六、作业布置
商店运来12箱啤酒,把它们堆放成长方体形状,它们的占地面积可能是多少平方分米?
七、教学反思
一、复习目标
1、使学生在整理和复习各种平面、立体图形的特征、各种图形之间的联系的基础上,复习和整理立体图形的表面积和体积计算方法。
2、使学生能熟练的运用立体图形的表面积和体积计算公式解决实际问题。
3、掌握立体图形的表面积体积计算公式的推导过程,了解它们之间的联系。
二、课时安排:1课时
三、复习重难点:使学生能熟练的运用立体图形的表面积和体积计算公式解决实际问题。
四、教学过程
(一)知识梳理
同学们以前我们学过立体图形的表面积和体积计算方法,我们学过的立体图形的体积计算公式是怎样推导出来的?它们之间有怎样的联系?
回顾整理要求:
1. 小组合作,回忆立体图形和立体图形的知识;
2. 根据知识间的关系合理地整理;
3. 把整理的结果用表格、流程图、树状图等自己喜欢的方式表示出来。
(二)题型、方法归纳
1、生讨论交流:
我们学过哪些立体图形?
长方体 正方体 圆柱 圆锥
这些立体图形的体积计算公式,是怎样推导出来的?
(1)长方体体积的推导:
长方体的体积 = 长×宽×高 V = ɑbh
长方体的体积 = 底面积×高 V = Sh
(2)正方体体积的推导:
正方体是长、宽、高都相等的长方体。
正方体的体积 = 棱长×棱长×棱长 V = ɑ3
长方体的体积 = 底面积×高 V = Sh
(3)圆柱体体积的推导:
转化成长方体,圆柱的体积 = 底面积×高 V = S h
(4)圆锥体体积的推导:
实验、转化圆锥的体积是等底等高的圆柱体积的 。
圆锥的体积 = × 底面积×高
师生小结:
2、这些体积计算公式之间有怎样的联系呢?
回顾整理:求圆柱的表面积所经历的思维过程。
3、怎样选择下面的材料制作一个水桶,有几种方案?
想一想,制作出的水桶可能是什么形状的?
水桶的形状可能是长方体的,水桶的形状可能是圆柱的
(1)水桶的侧面展开图是长方形,水桶的底面是圆形。62.8cm的边作为底面周长。
底面直径:62.8÷3.14=20(厘米)
可以选择长62.8cm、宽31.4cm的长方形做水桶侧面,底面直径为20cm的圆做水桶的底。
(2)水桶的侧面展开图是长方形,水桶的底面是圆形。31.4cm的边作为底面周长。
底面直径:31.4÷3.14=10(厘米)可以选择长62.8cm、宽31.4cm的长方形做水桶的侧面,底面直径为10cm的圆做水桶的底。
(3)水桶的侧面展开图是长方形,水桶的底面是正方形。
以62.8cm的边作为底面周长。正方形边长:62.8÷4=15.7(厘米)
可以选择长62.8cm、宽31.4cm的长方形做水桶的侧面,边长为15.7cm的正方形做水桶的底。
(4)水桶的侧面展开图是长方形,水桶的底面是正方形. 长方形的宽等于底面周长
正方形边长:31.4÷4=7.85(厘米)可以选择长62.8cm、宽31.4cm的长方形做水桶的侧面,边长为7.5cm的正方形做水桶的底。
(三)典例精讲
我们是怎样用转化的方法推导出立体图形的体积计算公式的?
(四)归纳小结
(五)随堂检测
1、求立体图形的体积和表面积。(只列式不计算)
2、一个长方体苹果箱的规格是40×30×25(单位:m),它的体积是多少立方厘米?制作10个这样的纸箱至少需要多少板纸?
3、用下面的五块玻璃做一个鱼缸,这个鱼缸的底面积是多少?它能装多少升水?(玻璃的厚度不计)
4、一个正方体水箱,棱长是40厘米。如果将一个石块浸入水中,水面上升2厘米。这个石块的体积是多少?
5、瓶子里装着一些水(如下图所示),瓶底面积是0.8平方分米,请你想办法计算瓶子的容积。
五、板书设计
立体图形的体积和表面积
立体图形的体积推导
问题 想象 选择 计算 答案
立体 平面 立体
不规则图形转化成规则物体
六、作业布置
商店运来12箱啤酒,把它们堆放成长方体形状,它们的占地面积可能是多少平方分米?
七、教学反思
