2022年人教版八年级数学 下册 17.1 勾股定理 第1课时 勾股定理 课件(共32张)
文档属性
| 名称 | 2022年人教版八年级数学 下册 17.1 勾股定理 第1课时 勾股定理 课件(共32张) |  | |
| 格式 | zip | ||
| 文件大小 | 962.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 10:15:23 | ||
图片预览








文档简介
(共32张PPT)
国际数学家大会是最高水平的全球性数学科学学术
会议.我国首都北京曾召开了第24届国际数学家大会.如图就是大会的会徽的图案.
请你说说这个图案由哪些基本图形组成?
导入新课
17.1 勾股定理
人教版八年级数学 下册
第1课时 勾股定理
学习目标
1、了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理;
2、介绍我国古代在勾股定理研究方面所取得的成就,激发爱国热情,勤奋学习.
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用砖铺成的地面(如下图所示):
毕达哥拉斯
A
B
C
穿越毕达哥拉斯做客现场
问题1 试问A、B、C面积之间有什么样的数量关系?
正方形A的面积
正方形B的面积
正方形C的面积
+
=
目标导学一:勾股定理的认识及验证
A
B
C
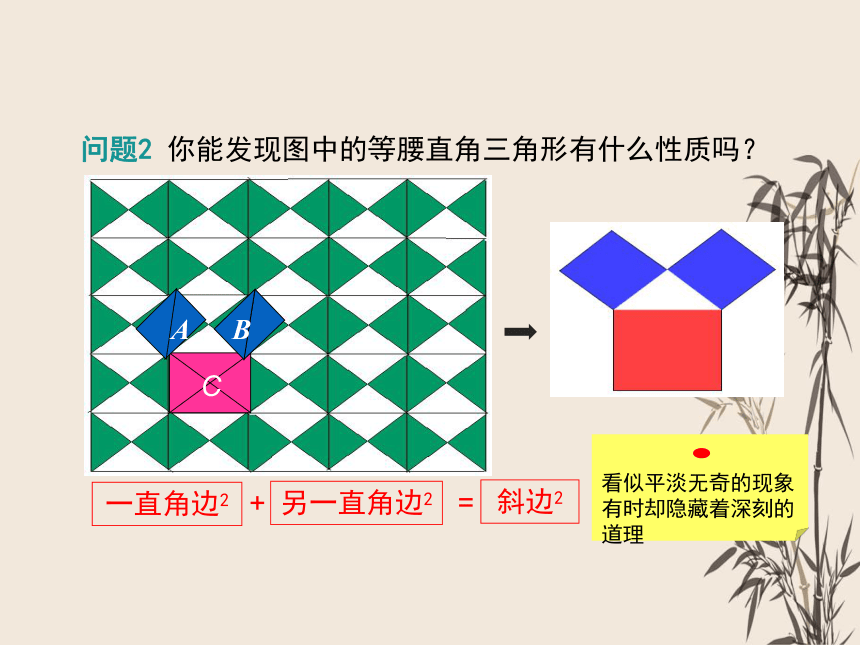
问题2 你能发现图中的等腰直角三角形有什么性质吗?
一直角边2
另一直角边2
斜边2
+
=
看似平淡无奇的现象有时却隐藏着深刻的道理
图1-2
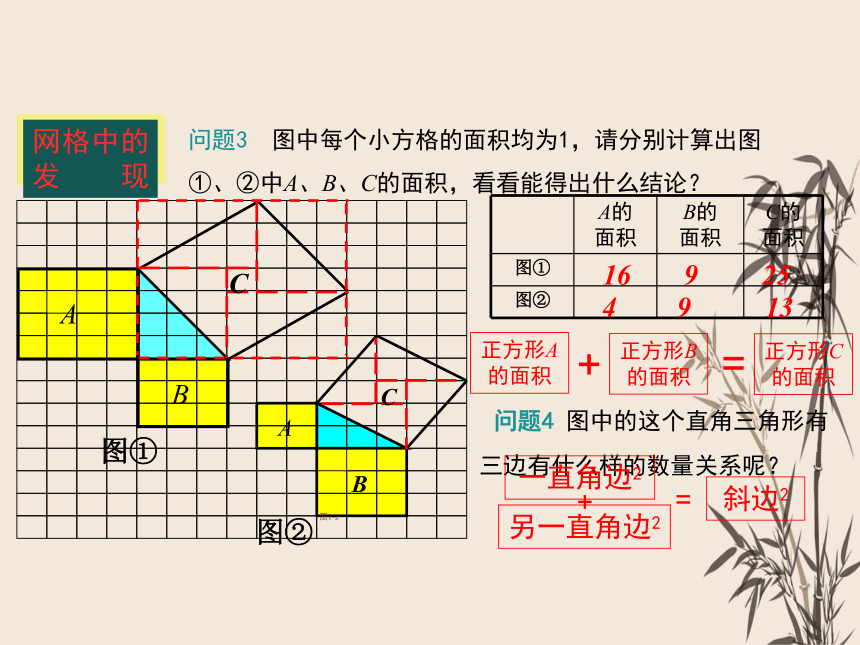
问题3 图中每个小方格的面积均为1,请分别计算出图①、②中A、B、C的面积,看看能得出什么结论?
图①
图②
A
B
A
B
C
C
A的 面积 B的 面积 C的
面积
图①
图②
16
9
25
4
9
13
网格中的发现
正方形A的面积
正方形B的面积
正方形C的面积
+
=
问题4 图中的这个直角三角形有三边有什么样的数量关系呢?
一直角边2
另一直角边2
斜边2
+
=
这个图案是公元3世纪我国汉代的赵爽在注解《周
髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根
据此图指出:四个全等的直角三角形(红色)可以如图
围成一个大正方形,中间的部分是一个小正方形 (黄
色).勾股定理在数学发展中起
到了重大的作用,其证明方法据
说有400 多种,有兴趣的同学可
以继续研究,或到网上查阅勾股
定理的相关资料.
c
b
a
(
b
-
a
)
2
黄实
朱实
拓展阅读
命题 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
由上面的例子,我们猜想:
a
b
c
BY YUSHEN
b
a
c
a+b
a
b
c
c
c
c
a
b
c
c
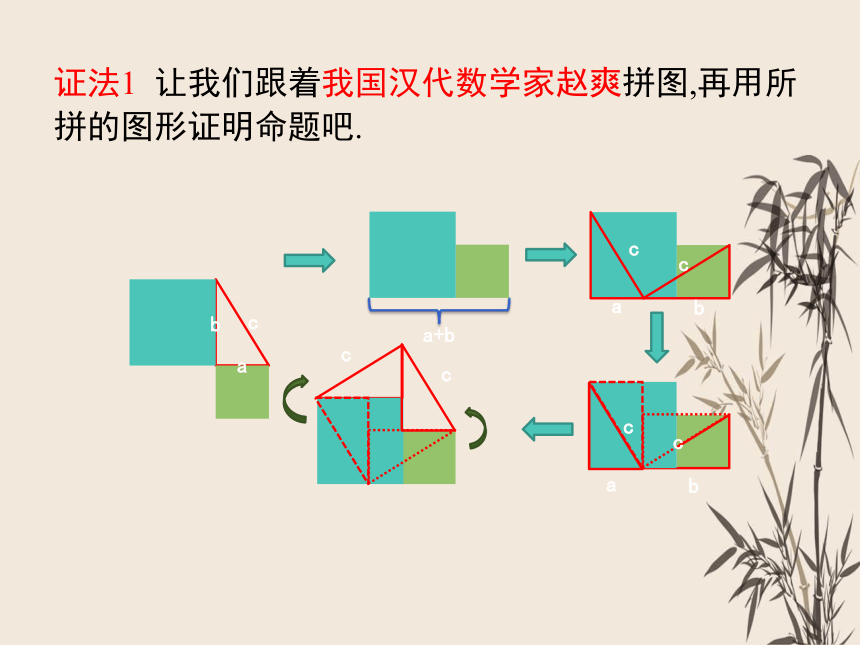
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
c
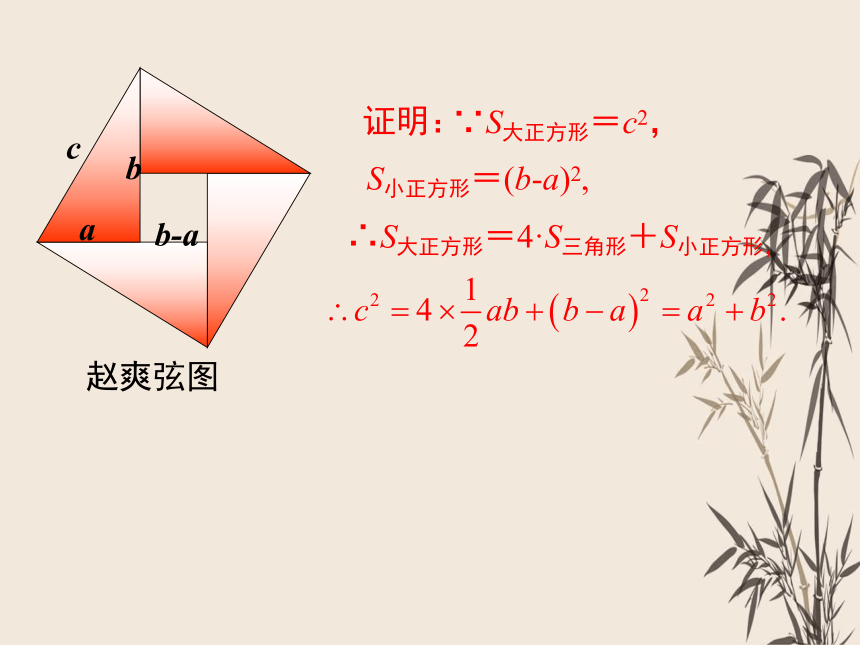
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
赵爽所用的这种方法是我国古代常用的“出入相补法”.在西方,人们称勾股定理为毕达哥拉斯定理.
赵爽弦图
c
b
a
黄
实
朱实
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际.以至于古往今来,上至帝王总统都愿意探讨、研究它的证明,新的证法不断出现.建议同学们课外认真阅读P30《勾股定理的证明》.
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
BY YUSHEN
毕达哥拉斯是古希腊数学家、哲学家。他出生在爱琴海中的萨摩斯岛(今希腊东部小岛),自幼聪明好学,曾在名师门下学习几何学、自然科学和哲学。
几何学中,有着无数定理,毕达哥拉斯定理是其中最诱人的一个,是人类科学发现中的一条基本定理,对科技进步起了不可估量的作用。中世纪德国数学家、天文学家开普勒称赞说:“几何学中有两件瑰宝,一是毕达哥拉斯定理,一是黄金分割律。”
a
a
b
b
c
c
∴a2 + b2 = c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
归纳总结
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
勾股定理揭示了直角三角形三边之间的关系.
判断题
(1)若a、b、c是三角形的三边,则 . ( )
(2)直角三角形中,两边的平方和等于第三边 的平方. ( )
×
×
练一练
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
小贴士
例1.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
归纳
目标导学二:利用勾股定理进行计算
例2 已知:Rt△ABC中,AB=4,AC=3,则BC= .
5 或
4
3
A
C
B
4
3
C
A
B
温馨提示 当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下,一定要进行分类讨论,否则容易丢解.
1.如图,所有的三角形都是直角三角形,四
边形都是正方形,已知正方形A,B,C,D 的边长分别
是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
即学即练
2.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.
由勾股定理得152+ x2 =172,
即x2=172-152=289–225=64,
∴ x=±8(负值舍去),
∴另一直角边长为8 cm,
直角三角形的面积是
(cm2).
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
课堂小结
BY YUSHEN
1.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
A.3 B.5 C.6 D.4
检测目标
B
BY YUSHEN
2.在直角坐标系中,已知点P的坐标为(5,12),则点P到原点的距离是( )
A.5 B.12 C.13 D.17
检测目标
C
BY YUSHEN
3.在下列四组数中,不是勾股数的一组数是( )
A.a=15,b=8,c=17
B.a=9,b=12,c=15
C.a=7,b=24,c=25
D.a=3,b=5,c=7
检测目标
D
BY YUSHEN
4.已知a=3,b=4,若a,b,c能组成直角三角形,则c=( )
A.5 B.
C.5或 D.5或6
检测目标
C
5.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
国际数学家大会是最高水平的全球性数学科学学术
会议.我国首都北京曾召开了第24届国际数学家大会.如图就是大会的会徽的图案.
请你说说这个图案由哪些基本图形组成?
导入新课
17.1 勾股定理
人教版八年级数学 下册
第1课时 勾股定理
学习目标
1、了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理;
2、介绍我国古代在勾股定理研究方面所取得的成就,激发爱国热情,勤奋学习.
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用砖铺成的地面(如下图所示):
毕达哥拉斯
A
B
C
穿越毕达哥拉斯做客现场
问题1 试问A、B、C面积之间有什么样的数量关系?
正方形A的面积
正方形B的面积
正方形C的面积
+
=
目标导学一:勾股定理的认识及验证
A
B
C
问题2 你能发现图中的等腰直角三角形有什么性质吗?
一直角边2
另一直角边2
斜边2
+
=
看似平淡无奇的现象有时却隐藏着深刻的道理
图1-2
问题3 图中每个小方格的面积均为1,请分别计算出图①、②中A、B、C的面积,看看能得出什么结论?
图①
图②
A
B
A
B
C
C
A的 面积 B的 面积 C的
面积
图①
图②
16
9
25
4
9
13
网格中的发现
正方形A的面积
正方形B的面积
正方形C的面积
+
=
问题4 图中的这个直角三角形有三边有什么样的数量关系呢?
一直角边2
另一直角边2
斜边2
+
=
这个图案是公元3世纪我国汉代的赵爽在注解《周
髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根
据此图指出:四个全等的直角三角形(红色)可以如图
围成一个大正方形,中间的部分是一个小正方形 (黄
色).勾股定理在数学发展中起
到了重大的作用,其证明方法据
说有400 多种,有兴趣的同学可
以继续研究,或到网上查阅勾股
定理的相关资料.
c
b
a
(
b
-
a
)
2
黄实
朱实
拓展阅读
命题 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
由上面的例子,我们猜想:
a
b
c
BY YUSHEN
b
a
c
a+b
a
b
c
c
c
c
a
b
c
c
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
赵爽所用的这种方法是我国古代常用的“出入相补法”.在西方,人们称勾股定理为毕达哥拉斯定理.
赵爽弦图
c
b
a
黄
实
朱实
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际.以至于古往今来,上至帝王总统都愿意探讨、研究它的证明,新的证法不断出现.建议同学们课外认真阅读P30《勾股定理的证明》.
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
BY YUSHEN
毕达哥拉斯是古希腊数学家、哲学家。他出生在爱琴海中的萨摩斯岛(今希腊东部小岛),自幼聪明好学,曾在名师门下学习几何学、自然科学和哲学。
几何学中,有着无数定理,毕达哥拉斯定理是其中最诱人的一个,是人类科学发现中的一条基本定理,对科技进步起了不可估量的作用。中世纪德国数学家、天文学家开普勒称赞说:“几何学中有两件瑰宝,一是毕达哥拉斯定理,一是黄金分割律。”
a
a
b
b
c
c
∴a2 + b2 = c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
归纳总结
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
勾股定理揭示了直角三角形三边之间的关系.
判断题
(1)若a、b、c是三角形的三边,则 . ( )
(2)直角三角形中,两边的平方和等于第三边 的平方. ( )
×
×
练一练
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
小贴士
例1.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
归纳
目标导学二:利用勾股定理进行计算
例2 已知:Rt△ABC中,AB=4,AC=3,则BC= .
5 或
4
3
A
C
B
4
3
C
A
B
温馨提示 当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下,一定要进行分类讨论,否则容易丢解.
1.如图,所有的三角形都是直角三角形,四
边形都是正方形,已知正方形A,B,C,D 的边长分别
是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
即学即练
2.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.
由勾股定理得152+ x2 =172,
即x2=172-152=289–225=64,
∴ x=±8(负值舍去),
∴另一直角边长为8 cm,
直角三角形的面积是
(cm2).
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
课堂小结
BY YUSHEN
1.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
A.3 B.5 C.6 D.4
检测目标
B
BY YUSHEN
2.在直角坐标系中,已知点P的坐标为(5,12),则点P到原点的距离是( )
A.5 B.12 C.13 D.17
检测目标
C
BY YUSHEN
3.在下列四组数中,不是勾股数的一组数是( )
A.a=15,b=8,c=17
B.a=9,b=12,c=15
C.a=7,b=24,c=25
D.a=3,b=5,c=7
检测目标
D
BY YUSHEN
4.已知a=3,b=4,若a,b,c能组成直角三角形,则c=( )
A.5 B.
C.5或 D.5或6
检测目标
C
5.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
