2022年人教版八年级数学 下册17.1 勾股定理 第2课时 勾股定理在实际生活中的应用 课件(共27张)
文档属性
| 名称 | 2022年人教版八年级数学 下册17.1 勾股定理 第2课时 勾股定理在实际生活中的应用 课件(共27张) |
|
|
| 格式 | zip | ||
| 文件大小 | 776.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 10:15:25 | ||
图片预览




文档简介
(共27张PPT)
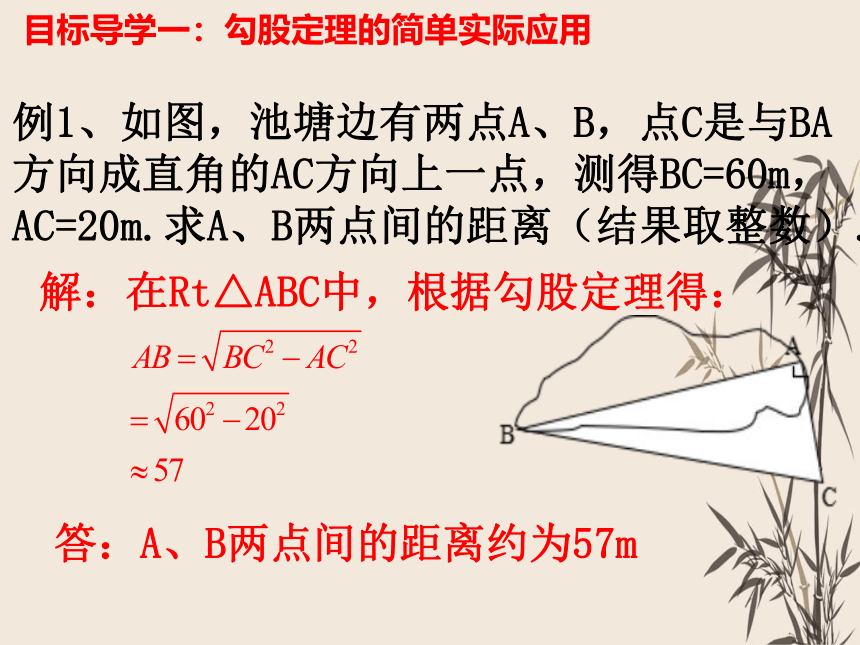
数学来源于生活,勾股定理的应用在生活中无处不在……
导入新课
2m
1m
A
B
D
C
17.1 勾股定理
人教版八年级数学 下册
第2课时 勾股定理在实际生活中的应用
学习目标
1. 会运用勾股定理求线段长及解决简单的实际问题。
2.能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长。
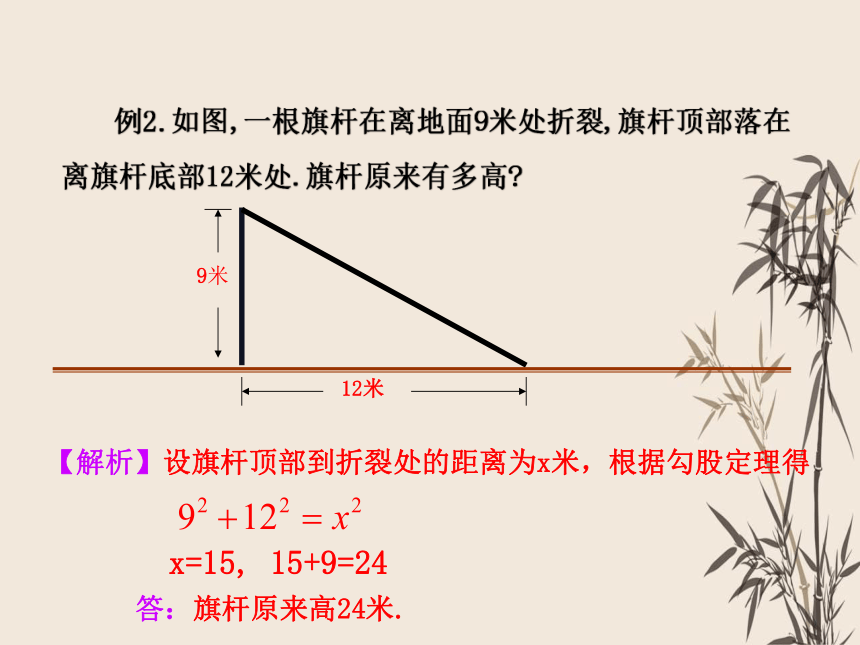
例1、如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m.求A、B两点间的距离(结果取整数).
解:在Rt△ABC中,根据勾股定理得:
答:A、B两点间的距离约为57m
目标导学一:勾股定理的简单实际应用
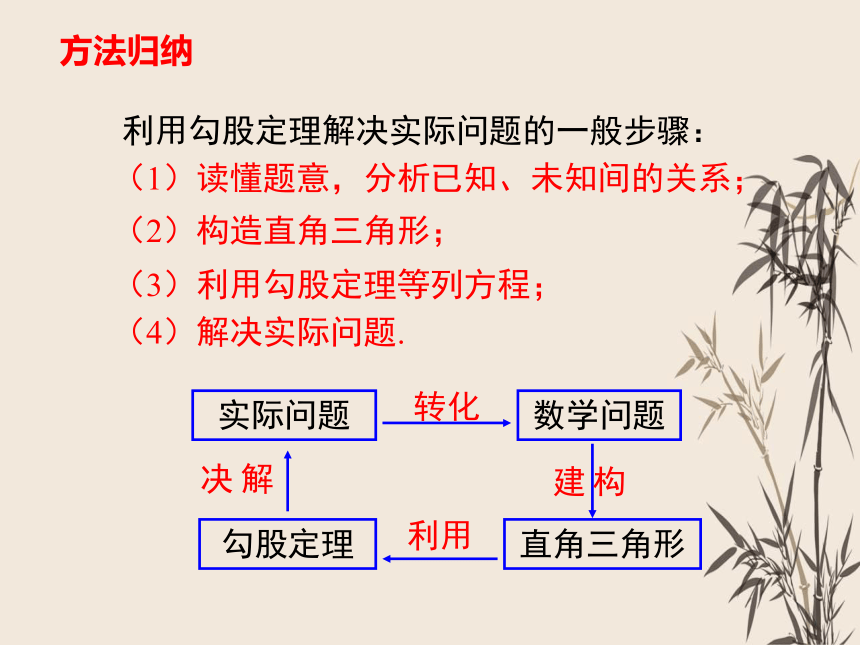
例2.如图,一根旗杆在离地面9米处折裂,旗杆顶部落在离旗杆底部12米处.旗杆原来有多高
12米
9米
【解析】设旗杆顶部到折裂处的距离为x米,根据勾股定理得
x=15, 15+9=24
答:旗杆原来高24米.
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
方法归纳
A
B
C
例3.如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长120cm.太阳能真空管AC有多长
【解析】在Rt△ABC中,由勾股定理,得
AC= = =150(cm)
答:太阳能真空管AC长150cm.
精典例题
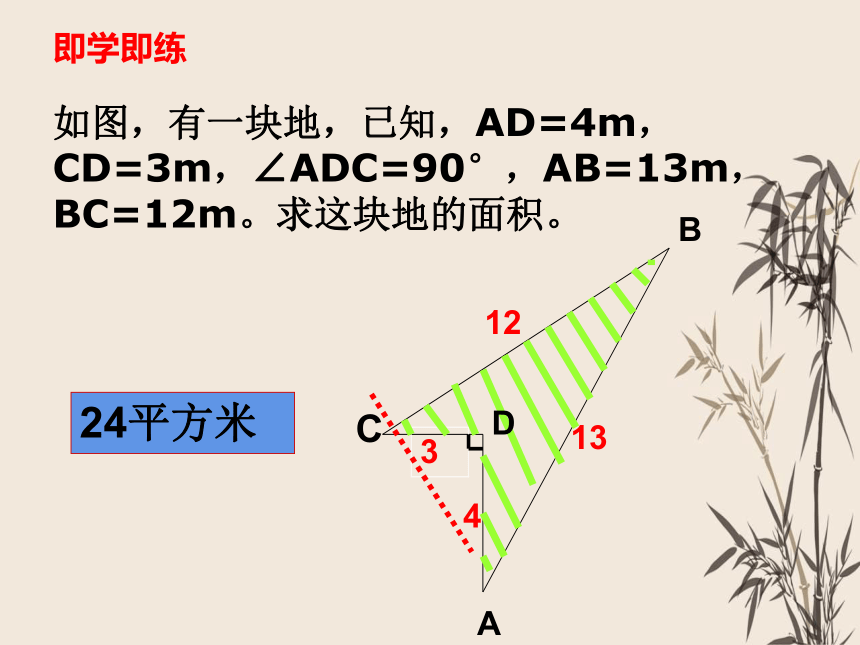
如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
即学即练
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
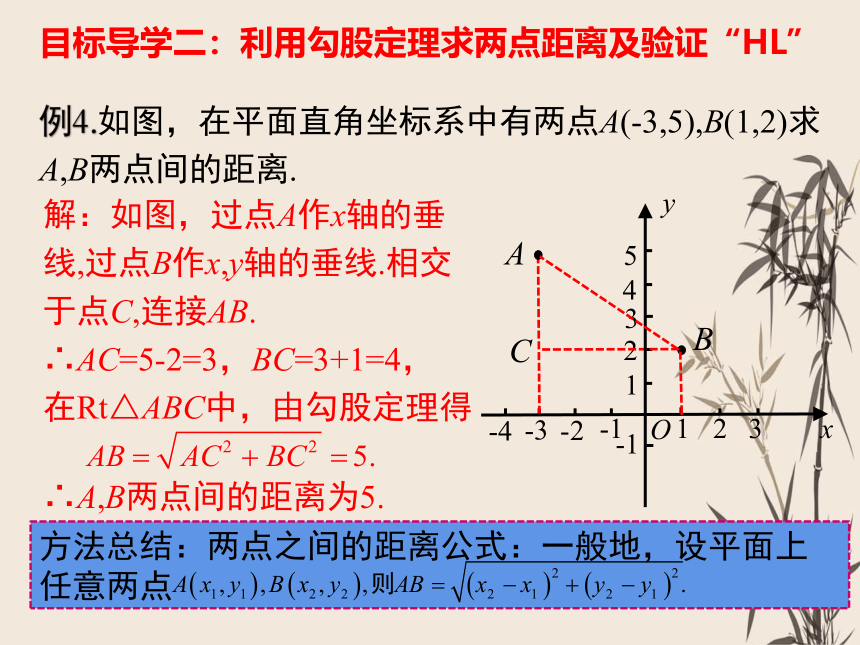
例4.如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
y
O
x
3
B
C
解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.
方法总结:两点之间的距离公式:一般地,设平面上任意两点
目标导学二:利用勾股定理求两点距离及验证“HL”
问题1 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全.
学习了勾股定理后,你能证明这一结论吗?
证明“HL”
′
′
′
′
′
′
已知:如图,在Rt△ABC 和Rt△A B C 中,∠C=
∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
证明:在Rt△ABC 和
Rt△A B C 中,∠C=∠C′
=90°,根据勾股定理,得
′
′
′
A
B
C
A
B
C′
′
′
证明“HL”
A
B
C
A
B
C′
′
′
′
′
′
∴ △ABC≌△A B C
(SSS).
′
′
′
′
′
′
证明:
∵ AB=A B ,
AC=A C ,
∴ BC=B C .
已知:如图,在Rt△ABC 和Rt△A B C 中,∠C=
∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
证明“HL”
C
B
A
问题 在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B路线,难道小狗也懂数学?
AC+CB >AB(两点之间线段最短)
思考 在立体图形中,怎么寻找最短线路呢?
目标导学三:利用勾股定理求最短距离
B
A
d
A
B
A'
A
B
B
A
O
想一想:蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
例5:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,蚂蚁怎么走最近?
B
A
根据两点之间线段最短易知第一个路线最近.
若已知圆柱体高为12 cm,底面半径为3 cm,π取3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在Rt△ABA′中,由勾股定理得
立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
归纳
数学思想:
立体图形
平面图形
转化
展开
例6、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
C
解:过B点向南作垂线,连结AB,可得Rt△ABC
由题意可知:AC=6千米,BC=8千米
根据勾股定理AB2=AC2+BC2
=62+82=100
∴AB=10千米
如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?
20
10
15
B
C
A
分析 根据题意分析蚂蚁爬行的路线有两种情况(如图①② ),由勾股定理可求得图1中AB最短.
①
B
A
20
10
15
5
AB =√202+152 =√625
B
AB =√102+252 =√725
②
A
20
10
15
5
即学即练
勾股定理
的应用
用勾股定理解决实际问题
用勾股定理解决点的距离及路径最短问题
解决“HL”判定方法证全等的正确性问题
课堂小结
1.如图,有一个三级台阶,它的每一级的长、宽、高分别为100 cm,15 cm和10 cm,A和B是这个台阶的两个相对的端点.若A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线的长度为( )
A.115 cm B.125 cm
C.135 cm D.145 cm
检测目标
B
2.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜( 如图 ).在三棱镜的侧面上,从顶点A到顶点A'镶有一圈金属丝.已知此三棱镜的高为8 cm,底面边长为2 cm,则这圈金属丝的长度至少为 cm.
检测目标
10
3.如图,厂房屋顶人字形钢架的跨度BC=12米,AB=AC=6.5米,则中柱AD( D为底边BC的中点 )的长是( )
A.6米 B.5米
C.3米 D.2.5米
检测目标
D
4.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( )
A.2.7米 B.2.5米 C.2米 D.1.8米
检测目标
A
5.今有池方一丈,芦苇生其中央,出水一尺,引芦苇赴岸,适与岸齐.问水深、芦苇长各几何?
A
B
C
分析:
可设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52= ,
通过解方程可得.
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
数学来源于生活,勾股定理的应用在生活中无处不在……
导入新课
2m
1m
A
B
D
C
17.1 勾股定理
人教版八年级数学 下册
第2课时 勾股定理在实际生活中的应用
学习目标
1. 会运用勾股定理求线段长及解决简单的实际问题。
2.能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长。
例1、如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m.求A、B两点间的距离(结果取整数).
解:在Rt△ABC中,根据勾股定理得:
答:A、B两点间的距离约为57m
目标导学一:勾股定理的简单实际应用
例2.如图,一根旗杆在离地面9米处折裂,旗杆顶部落在离旗杆底部12米处.旗杆原来有多高
12米
9米
【解析】设旗杆顶部到折裂处的距离为x米,根据勾股定理得
x=15, 15+9=24
答:旗杆原来高24米.
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
方法归纳
A
B
C
例3.如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长120cm.太阳能真空管AC有多长
【解析】在Rt△ABC中,由勾股定理,得
AC= = =150(cm)
答:太阳能真空管AC长150cm.
精典例题
如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
即学即练
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
例4.如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
y
O
x
3
B
C
解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.
方法总结:两点之间的距离公式:一般地,设平面上任意两点
目标导学二:利用勾股定理求两点距离及验证“HL”
问题1 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全.
学习了勾股定理后,你能证明这一结论吗?
证明“HL”
′
′
′
′
′
′
已知:如图,在Rt△ABC 和Rt△A B C 中,∠C=
∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
证明:在Rt△ABC 和
Rt△A B C 中,∠C=∠C′
=90°,根据勾股定理,得
′
′
′
A
B
C
A
B
C′
′
′
证明“HL”
A
B
C
A
B
C′
′
′
′
′
′
∴ △ABC≌△A B C
(SSS).
′
′
′
′
′
′
证明:
∵ AB=A B ,
AC=A C ,
∴ BC=B C .
已知:如图,在Rt△ABC 和Rt△A B C 中,∠C=
∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
证明“HL”
C
B
A
问题 在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B路线,难道小狗也懂数学?
AC+CB >AB(两点之间线段最短)
思考 在立体图形中,怎么寻找最短线路呢?
目标导学三:利用勾股定理求最短距离
B
A
d
A
B
A'
A
B
B
A
O
想一想:蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
例5:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,蚂蚁怎么走最近?
B
A
根据两点之间线段最短易知第一个路线最近.
若已知圆柱体高为12 cm,底面半径为3 cm,π取3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在Rt△ABA′中,由勾股定理得
立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
归纳
数学思想:
立体图形
平面图形
转化
展开
例6、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
C
解:过B点向南作垂线,连结AB,可得Rt△ABC
由题意可知:AC=6千米,BC=8千米
根据勾股定理AB2=AC2+BC2
=62+82=100
∴AB=10千米
如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?
20
10
15
B
C
A
分析 根据题意分析蚂蚁爬行的路线有两种情况(如图①② ),由勾股定理可求得图1中AB最短.
①
B
A
20
10
15
5
AB =√202+152 =√625
B
AB =√102+252 =√725
②
A
20
10
15
5
即学即练
勾股定理
的应用
用勾股定理解决实际问题
用勾股定理解决点的距离及路径最短问题
解决“HL”判定方法证全等的正确性问题
课堂小结
1.如图,有一个三级台阶,它的每一级的长、宽、高分别为100 cm,15 cm和10 cm,A和B是这个台阶的两个相对的端点.若A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线的长度为( )
A.115 cm B.125 cm
C.135 cm D.145 cm
检测目标
B
2.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜( 如图 ).在三棱镜的侧面上,从顶点A到顶点A'镶有一圈金属丝.已知此三棱镜的高为8 cm,底面边长为2 cm,则这圈金属丝的长度至少为 cm.
检测目标
10
3.如图,厂房屋顶人字形钢架的跨度BC=12米,AB=AC=6.5米,则中柱AD( D为底边BC的中点 )的长是( )
A.6米 B.5米
C.3米 D.2.5米
检测目标
D
4.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( )
A.2.7米 B.2.5米 C.2米 D.1.8米
检测目标
A
5.今有池方一丈,芦苇生其中央,出水一尺,引芦苇赴岸,适与岸齐.问水深、芦苇长各几何?
A
B
C
分析:
可设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52= ,
通过解方程可得.
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
