2022年人教版八年级数学下册 17.1 勾股定理 第3课时 利用勾股定理作图或计算 课件(共30张)
文档属性
| 名称 | 2022年人教版八年级数学下册 17.1 勾股定理 第3课时 利用勾股定理作图或计算 课件(共30张) |  | |
| 格式 | zip | ||
| 文件大小 | 749.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 10:15:29 | ||
图片预览









文档简介
(共30张PPT)
在数学中也有这样一幅美丽的“海螺型”图案,
如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?
导入新课
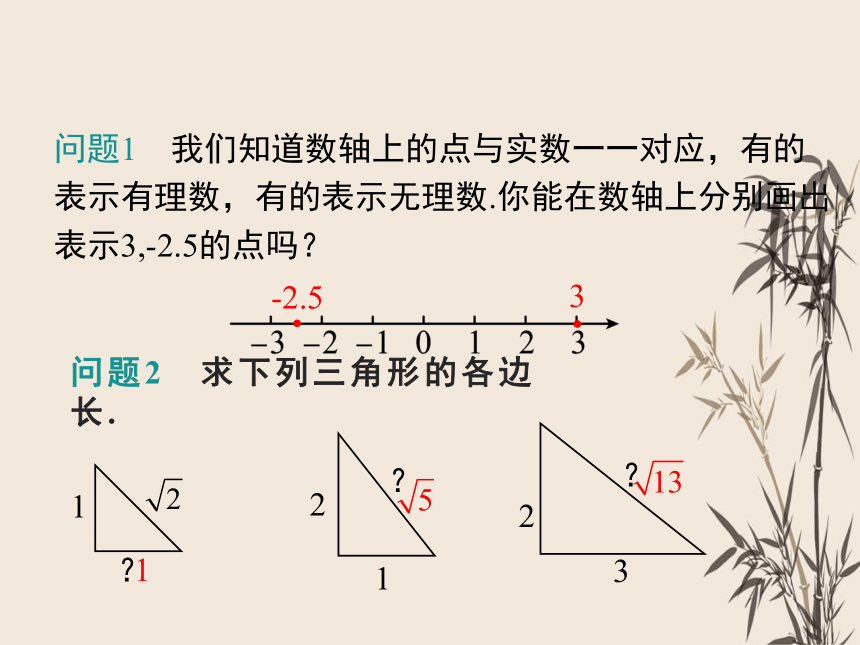
问题1 我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗?
3
-2.5
问题2 求下列三角形的各边长.
1
2
1
2
3
?
?
?
1
17.1 勾股定理
人教版八年级数学 下册
第3课时 利用勾股定理作图或计算
学习目标
1. 会运用勾股定理确定数轴上表示实数的点及解决
网格问题。
2.灵活运用勾股定理进行计算,并会运用勾股定理
解决相应的折叠问题。
实数
数轴上的点
一一对应
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗?
目标导学一:勾股定理与数轴
在数轴上作出表示无理数的点
1、两条直角边都是1的直角三角形的斜边长=____;
2、直角三角形一直角边长是3,另一直角边长是2,那么它的斜边长=_______.
作法:
(1)在数轴上找到点A,使OA=3;
(2)过点A作直线l垂直于OA,在l上取点B,使AB=2,那么OB=________;
(3)以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则OC=________.
如图,在数轴上,点C为表示_______的点.
2、在数轴上作出表示 点
A
l
B
C
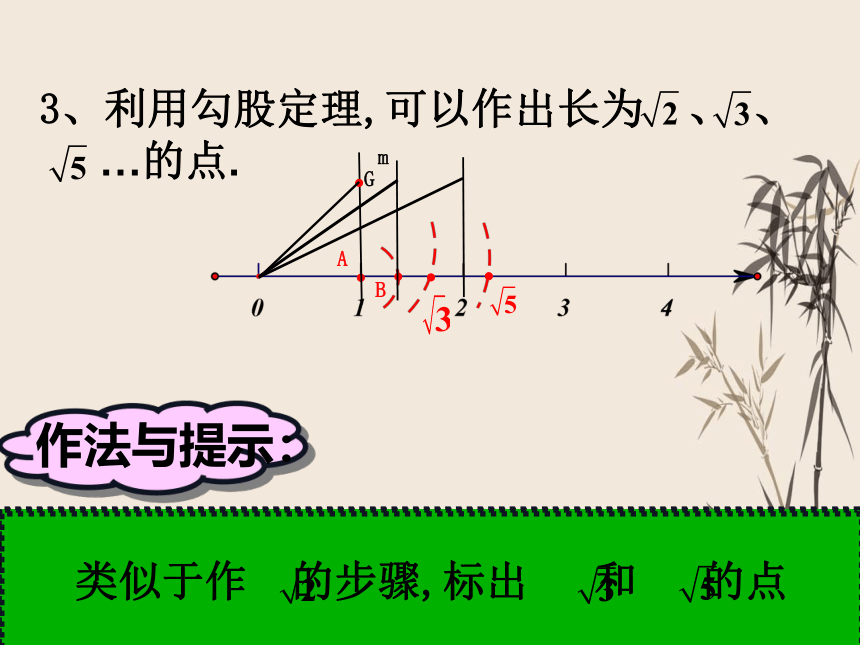
3、利用勾股定理,可以作出长为 、 、
…的点.
作法与提示:
A
(1)在数轴上标记点A,经过点A作OA的垂线m
m
(2)在m上取点K,使AG=1,连接OG
G
(3)以O为圆心OG为半径作弧,弧与数轴交于点B,
则点B的坐标就是
B
类似于作 的步骤,标出 和 的点
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
方法归纳
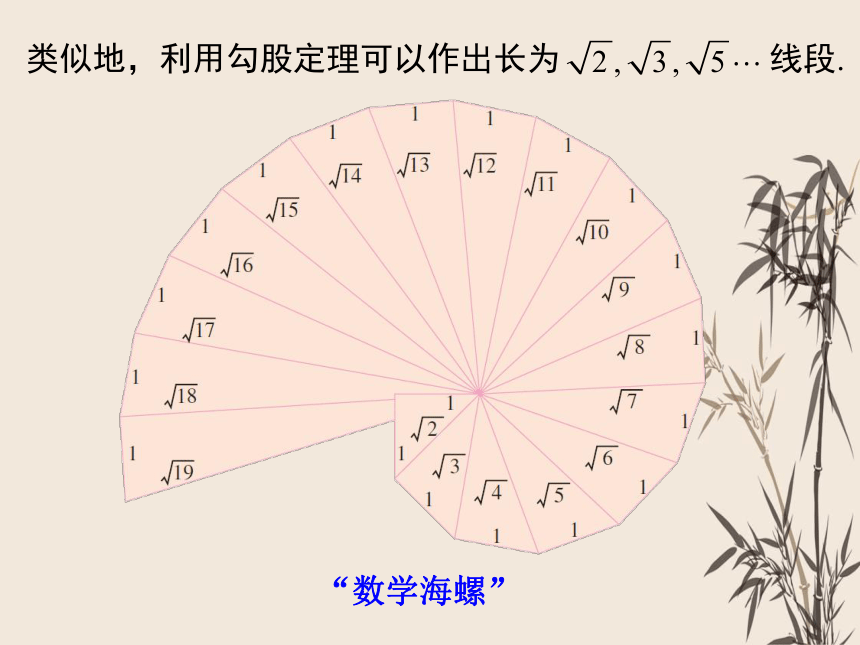
“数学海螺”
类似地,利用勾股定理可以作出长为 线段.
例1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
易错点拨:求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
精典例题
1.如图,点A表示的实数是 ( )
2.如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
C
D
练一练
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点,在图中画一个三角形,使它的三边分别为3, , .
作法与提示:
(1)在网格中,分别画出长度为3, , 的线
段,并如图标记点A、B、C、D
A
B
3
C
D
(2)以B为圆心,BC为半径作弧
以A为圆心,AD为半径作弧
两弧交于点O,连接AO,BO
则△ABO就是所求三角形
O
目标导学二:勾股定理与网格
例2 在如图所示的6×8的网格中,每个小正方形的边长都为1,写出格点△ABC各顶点的坐标,并求出此三角形的周长.
解:由题图得A(2,2),B(-2,-1),C(3,-2).
由勾股定理得
∴△ABC的周长为
勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
规律
例3 如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出多少条长度为 的线段?
解:如图所示,有8条.
一个点一个点的找,不要漏解.
1.勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度。
2.网格中求格点三角形的高的题,常用的方法是利用网格求面积,再用面积法求高。
方法归纳
例4 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得 x2+ 42=(8-x)2,
解得 x=3.
即EC的长为3cm.
要用到方程思想
目标导学三:勾股定理与图形的计算
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线数或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x的方程;
(4)解这个方程,从而求出所求线段长.
方法归纳
例、如图,等边三角形的边长是6,
求:(1)高AD的长;
(2)这个三角形的面积
解:(1)∵AD是等边三角形
ABC的高
∴AD平分∠BAC,∠BAC=30°
BD= AB=3
根据勾股定理:AD2=AB2-BD2
=62-32=27 ∴AD=
(2)这个三角形的面积
解:
= AB.AD
= ×6×3
=9
△ABC中,AB=10,AC=17,BC边上的高线AD=8,求线段BC的长和△ABC的面积.
A
B
C
17
10
8
D
8
6
15
15
6
21
或9
S△ABC=84或36
当题中没有给出图形时,应考虑图形的形状是否确定,如果不确定,就需要分类讨论。
即学即练
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
课堂小结
1.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
A
检测目标
2.如图,点C表示的数是( )
A.1 B.
C.1.5 D.
D
检测目标
3.如图,每个小正方形的边长均为1,则△ABC中, 长为无理数的边有( )
A.0条
B.1条
C.2条
D.3条
C
检测目标
4.如图是一张直角三角形的纸片,两直角边AC= 6 cm,BC=8 cm,现将△ABC折叠,使点B与点 A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm
C.6 cm D.10 cm
B
检测目标
5.若△ABC三边的长分别为 (a>0),请利用下图的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
解:如图,
∴△ABC即为所求,
A
B
C
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
在数学中也有这样一幅美丽的“海螺型”图案,
如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?
导入新课
问题1 我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗?
3
-2.5
问题2 求下列三角形的各边长.
1
2
1
2
3
?
?
?
1
17.1 勾股定理
人教版八年级数学 下册
第3课时 利用勾股定理作图或计算
学习目标
1. 会运用勾股定理确定数轴上表示实数的点及解决
网格问题。
2.灵活运用勾股定理进行计算,并会运用勾股定理
解决相应的折叠问题。
实数
数轴上的点
一一对应
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗?
目标导学一:勾股定理与数轴
在数轴上作出表示无理数的点
1、两条直角边都是1的直角三角形的斜边长=____;
2、直角三角形一直角边长是3,另一直角边长是2,那么它的斜边长=_______.
作法:
(1)在数轴上找到点A,使OA=3;
(2)过点A作直线l垂直于OA,在l上取点B,使AB=2,那么OB=________;
(3)以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则OC=________.
如图,在数轴上,点C为表示_______的点.
2、在数轴上作出表示 点
A
l
B
C
3、利用勾股定理,可以作出长为 、 、
…的点.
作法与提示:
A
(1)在数轴上标记点A,经过点A作OA的垂线m
m
(2)在m上取点K,使AG=1,连接OG
G
(3)以O为圆心OG为半径作弧,弧与数轴交于点B,
则点B的坐标就是
B
类似于作 的步骤,标出 和 的点
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
方法归纳
“数学海螺”
类似地,利用勾股定理可以作出长为 线段.
例1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
易错点拨:求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
精典例题
1.如图,点A表示的实数是 ( )
2.如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
C
D
练一练
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点,在图中画一个三角形,使它的三边分别为3, , .
作法与提示:
(1)在网格中,分别画出长度为3, , 的线
段,并如图标记点A、B、C、D
A
B
3
C
D
(2)以B为圆心,BC为半径作弧
以A为圆心,AD为半径作弧
两弧交于点O,连接AO,BO
则△ABO就是所求三角形
O
目标导学二:勾股定理与网格
例2 在如图所示的6×8的网格中,每个小正方形的边长都为1,写出格点△ABC各顶点的坐标,并求出此三角形的周长.
解:由题图得A(2,2),B(-2,-1),C(3,-2).
由勾股定理得
∴△ABC的周长为
勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
规律
例3 如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出多少条长度为 的线段?
解:如图所示,有8条.
一个点一个点的找,不要漏解.
1.勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度。
2.网格中求格点三角形的高的题,常用的方法是利用网格求面积,再用面积法求高。
方法归纳
例4 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得 x2+ 42=(8-x)2,
解得 x=3.
即EC的长为3cm.
要用到方程思想
目标导学三:勾股定理与图形的计算
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线数或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x的方程;
(4)解这个方程,从而求出所求线段长.
方法归纳
例、如图,等边三角形的边长是6,
求:(1)高AD的长;
(2)这个三角形的面积
解:(1)∵AD是等边三角形
ABC的高
∴AD平分∠BAC,∠BAC=30°
BD= AB=3
根据勾股定理:AD2=AB2-BD2
=62-32=27 ∴AD=
(2)这个三角形的面积
解:
= AB.AD
= ×6×3
=9
△ABC中,AB=10,AC=17,BC边上的高线AD=8,求线段BC的长和△ABC的面积.
A
B
C
17
10
8
D
8
6
15
15
6
21
或9
S△ABC=84或36
当题中没有给出图形时,应考虑图形的形状是否确定,如果不确定,就需要分类讨论。
即学即练
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来
通常用到方程思想
课堂小结
1.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
A
检测目标
2.如图,点C表示的数是( )
A.1 B.
C.1.5 D.
D
检测目标
3.如图,每个小正方形的边长均为1,则△ABC中, 长为无理数的边有( )
A.0条
B.1条
C.2条
D.3条
C
检测目标
4.如图是一张直角三角形的纸片,两直角边AC= 6 cm,BC=8 cm,现将△ABC折叠,使点B与点 A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm
C.6 cm D.10 cm
B
检测目标
5.若△ABC三边的长分别为 (a>0),请利用下图的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
解:如图,
∴△ABC即为所求,
A
B
C
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
