2021-2022学年数学人教版七年级下册6.3实数第一课时课件(19张)
文档属性
| 名称 | 2021-2022学年数学人教版七年级下册6.3实数第一课时课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 533.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 10:47:39 | ||
图片预览






文档简介
(共19张PPT)
6.3 实数
第六章 实 数
第1课时 实 数
复习导入
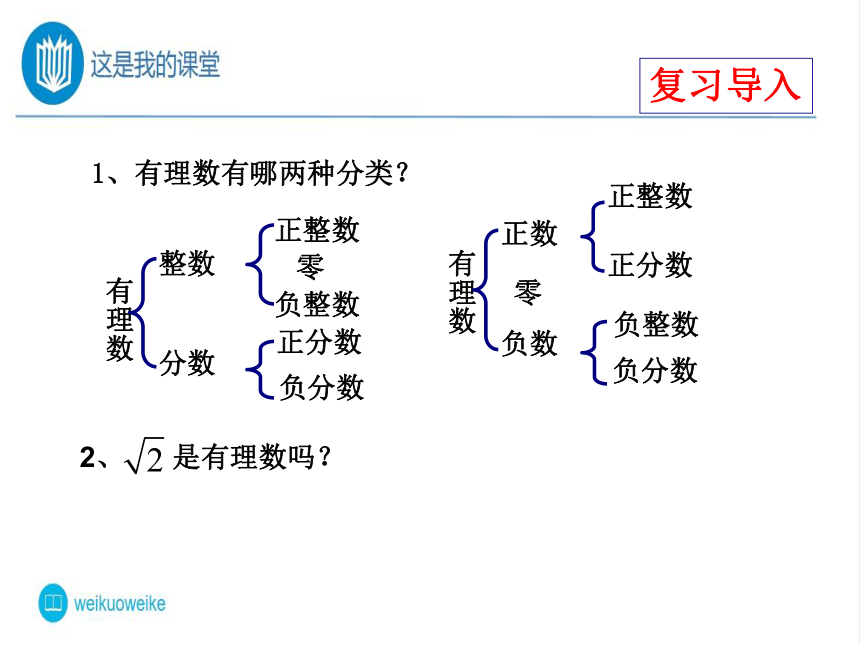
1、有理数有哪两种分类?
2、 是有理数吗?
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正数
负数
正整数
零
负整数
正分数
负分数
问题1 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
任何一个有理数都能写成有限小数或无限循环小数的形式;
反过来任何有限小数或无限循环小数也都是有理数。
还有其他类型的小数吗?
1.自学教材第第53-54页内容,并注意重点内容多读几遍。
自学指导
学习新知
叫做无理数.
想一想:所有的数都可以写成有限小数和无限循环小数的形式吗?
π=3.1415926535897932384626…
无限不循环小数
不是.如:
常见的一些无理数:
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
无理数的概念:无限不循环小数叫无理数.
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
例 把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,点O' 对应的数是多少?
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示无理数的点吗?
为什么?
0
1
2
4
3
-1
-2
问题:边长为1的正方形,对角线长为多少
事实上:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
你能把 在数轴上表示出来吗?请与同桌一起试一试,说说你的办法。
实数与数轴上的有什么关系?
每一个无理数都可以用数轴上的一个点表示出来,这就是说,数轴上的点有些表示有理数,有些表示无理数;当从有理数扩充到实数以后,实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的点来表示;
反过来,数轴上的每一个点都是表示一个实数.与规定有理数的大小一样,对于数轴上的任意两个点,右边的点所表示的实数总比左边的点表示的实数大.
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
学生展示
无理数:
有理数:
负实数:
正实数:
例1 将下列各数分别填入下列相应的括号内:
课堂提升
1.下列说法正确的是( )
A.a一定是正实数
B. 是有理数
C. 是有理数
D.数轴上任一点都对应一个有理数
B
课堂提升
2.把下列各数填入相应的集合内:
(1)有理数集合:{
(2)无理数集合:{
(3)整数集合:{
(4)负数集合:{
(5)分数集合:{
(6)实数集合:{
}
}
}
}
}
}
3.比较3,4, 的大小.
解:33 = 27,43 = 64
因为27 < 50 < 64
所以3 < < 4
课堂小结
1.概念:无理数和实数.
2.特点:有理数和无理数.
3.关系:实数与数轴的对应关系.
4.数学思想:
类比、数形结合、分类的思想.
学习贵在坚持
6.3 实数
第六章 实 数
第1课时 实 数
复习导入
1、有理数有哪两种分类?
2、 是有理数吗?
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正数
负数
正整数
零
负整数
正分数
负分数
问题1 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
任何一个有理数都能写成有限小数或无限循环小数的形式;
反过来任何有限小数或无限循环小数也都是有理数。
还有其他类型的小数吗?
1.自学教材第第53-54页内容,并注意重点内容多读几遍。
自学指导
学习新知
叫做无理数.
想一想:所有的数都可以写成有限小数和无限循环小数的形式吗?
π=3.1415926535897932384626…
无限不循环小数
不是.如:
常见的一些无理数:
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
无理数的概念:无限不循环小数叫无理数.
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
例 把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,点O' 对应的数是多少?
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示无理数的点吗?
为什么?
0
1
2
4
3
-1
-2
问题:边长为1的正方形,对角线长为多少
事实上:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
你能把 在数轴上表示出来吗?请与同桌一起试一试,说说你的办法。
实数与数轴上的有什么关系?
每一个无理数都可以用数轴上的一个点表示出来,这就是说,数轴上的点有些表示有理数,有些表示无理数;当从有理数扩充到实数以后,实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的点来表示;
反过来,数轴上的每一个点都是表示一个实数.与规定有理数的大小一样,对于数轴上的任意两个点,右边的点所表示的实数总比左边的点表示的实数大.
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
学生展示
无理数:
有理数:
负实数:
正实数:
例1 将下列各数分别填入下列相应的括号内:
课堂提升
1.下列说法正确的是( )
A.a一定是正实数
B. 是有理数
C. 是有理数
D.数轴上任一点都对应一个有理数
B
课堂提升
2.把下列各数填入相应的集合内:
(1)有理数集合:{
(2)无理数集合:{
(3)整数集合:{
(4)负数集合:{
(5)分数集合:{
(6)实数集合:{
}
}
}
}
}
}
3.比较3,4, 的大小.
解:33 = 27,43 = 64
因为27 < 50 < 64
所以3 < < 4
课堂小结
1.概念:无理数和实数.
2.特点:有理数和无理数.
3.关系:实数与数轴的对应关系.
4.数学思想:
类比、数形结合、分类的思想.
学习贵在坚持
