人教版数学六年级下册3.《圆柱与圆锥》第四课时 解决问题 课件(共21张PPT)
文档属性
| 名称 | 人教版数学六年级下册3.《圆柱与圆锥》第四课时 解决问题 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 18:29:27 | ||
图片预览







文档简介
(共21张PPT)
2022年春人教版数学
六年级下册数学精品课件
《圆柱与圆锥》
第四课时 解决问题
小学数学
情境导入
今天老师带来了一个矿泉水瓶,它的标签没有了,要怎么通过计算得出它的容积呢?
讨论一下
探究新知
7cm
18cm
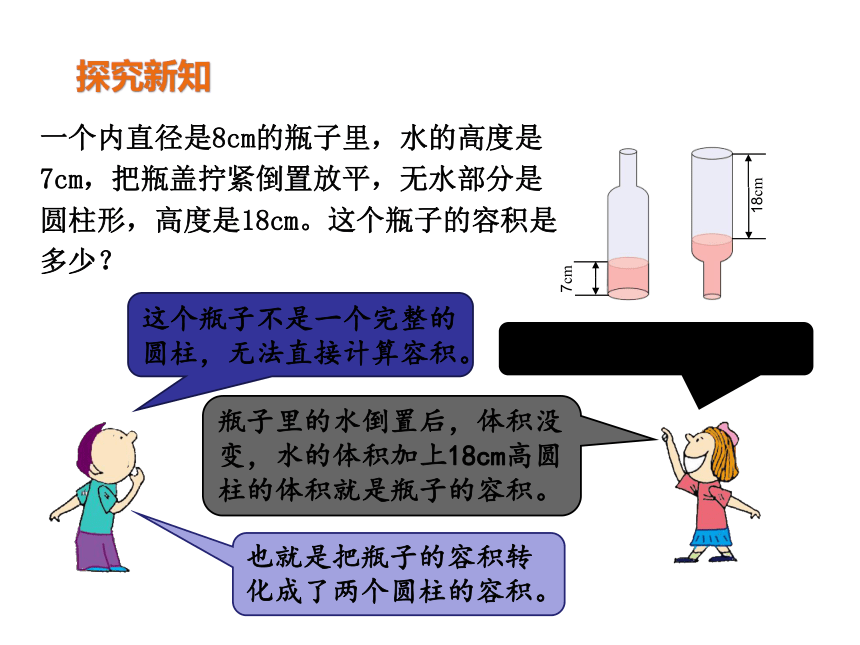
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
这个瓶子不是一个完整的圆柱,无法直接计算容积。
能不能转化成圆柱呢?
瓶子里的水倒置后,体积没变,水的体积加上18cm高圆柱的体积就是瓶子的容积。
也就是把瓶子的容积转化成了两个圆柱的容积。
探究新知
7cm
18cm
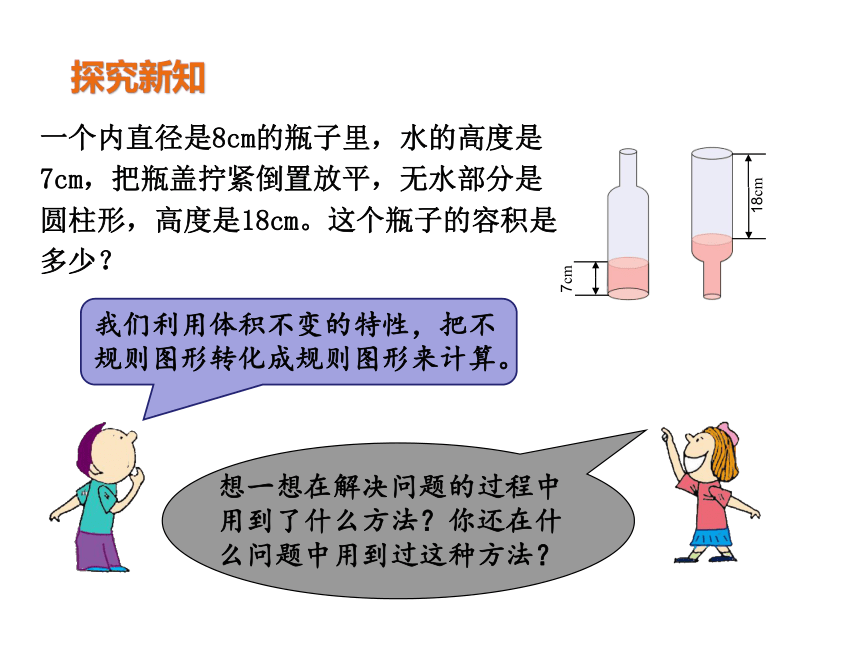
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
瓶子的容积:
3.14×(8÷2)2 ×7+ 3.14 ×(8÷2)2 ×18
=3.14×16 ×(7+18)
=3.14×16×25
=1256(cm3)
=1256(mL)
答:瓶子的容积是1256mL。
探究新知
7cm
18cm
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
我们利用体积不变的特性,把不规则图形转化成规则图形来计算。
想一想在解决问题的过程中用到了什么方法?你还在什么问题中用到过这种方法?
探究新知
10cm
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
请你仔细想一想,小明喝了的水的体积该怎么计算呢?
无水部分高为10cm圆柱体积就是小明喝了的水的体积。
探究新知
10cm
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
答:小明喝了282.6mL的水。
易错举例
把一块长31.4cm、宽2cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
31.4×2×4÷4
=251.2÷4
=62.8(cm)
答:圆柱的高是62.8cm。
这样解对吗?
×
易错举例
把一块长31.4cm、宽2cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
把长方体熔铸成圆柱,体积没有发生变化,长方体的体积等于圆柱的体积,再通过圆柱体积÷圆柱底面积=高的公式可求出圆柱的高。
温馨提示:在解决圆柱的体积相关的实际问题时,要注意题中的变量与不变量。
巩固拓展
如下图,一个底面周长为9.42厘米的圆柱体,从中间斜着截去一段后,它的体积是多少?
4厘米
6厘米
想一想,如果把不规则的部分从中间分成两份,在重新拼在一起,能得到一个什么图形?
巩固拓展
如下图,一个底面周长为9.42厘米的圆柱体,从中间斜着截去一段后,它的体积是多少?
从侧面横截面观察
巩固拓展
如下图,一个底面周长为9.42厘米的圆柱体,从中间斜着截去一段后,它的体积是多少?
解法一:
3.14×(9.42÷3.14÷2)2 ×10÷2
=35.325(立方厘米)
解法二:
3.14×(9.42÷3.14÷2)2 ×4+3.14×(9.42÷3.14÷2)2 ×2÷2
=3.14×1.52 ×5
=35.325(立方厘米)
答:它的体积是35.325立方厘米。
巩固拓展
下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
请你想一想,上面4个图形当以长为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试。
图1
图2
图3
图4
巩固拓展
下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
设π=3
图1
图2
图3
图4
图1
半径:18÷3÷2=3(dm)
图2
半径:12÷3÷2=2(dm)
图3
半径:9÷3÷2=1.5(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×3 ×2=54(dm )
体积:3×2 ×3=36(dm )
体积:3×1.5 ×4=27(dm )
体积:3×1 ×6=18(dm )
答:图4圆柱的体积最小,图1圆柱的体积最大。
巩固拓展
下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
图1
图2
图3
图4
我发现,上面4个图形。当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。
课堂小结
求不规则物体的体积或容积,可以利用转化的思想方法,将其转化为规则的图形进行计算。
课后作业
完成课后对应内容。
祝 你 学 习 进 步!
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
六年级下册数学精品课件
《圆柱与圆锥》
第四课时 解决问题
小学数学
情境导入
今天老师带来了一个矿泉水瓶,它的标签没有了,要怎么通过计算得出它的容积呢?
讨论一下
探究新知
7cm
18cm
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
这个瓶子不是一个完整的圆柱,无法直接计算容积。
能不能转化成圆柱呢?
瓶子里的水倒置后,体积没变,水的体积加上18cm高圆柱的体积就是瓶子的容积。
也就是把瓶子的容积转化成了两个圆柱的容积。
探究新知
7cm
18cm
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
瓶子的容积:
3.14×(8÷2)2 ×7+ 3.14 ×(8÷2)2 ×18
=3.14×16 ×(7+18)
=3.14×16×25
=1256(cm3)
=1256(mL)
答:瓶子的容积是1256mL。
探究新知
7cm
18cm
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
我们利用体积不变的特性,把不规则图形转化成规则图形来计算。
想一想在解决问题的过程中用到了什么方法?你还在什么问题中用到过这种方法?
探究新知
10cm
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
请你仔细想一想,小明喝了的水的体积该怎么计算呢?
无水部分高为10cm圆柱体积就是小明喝了的水的体积。
探究新知
10cm
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
答:小明喝了282.6mL的水。
易错举例
把一块长31.4cm、宽2cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
31.4×2×4÷4
=251.2÷4
=62.8(cm)
答:圆柱的高是62.8cm。
这样解对吗?
×
易错举例
把一块长31.4cm、宽2cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
把长方体熔铸成圆柱,体积没有发生变化,长方体的体积等于圆柱的体积,再通过圆柱体积÷圆柱底面积=高的公式可求出圆柱的高。
温馨提示:在解决圆柱的体积相关的实际问题时,要注意题中的变量与不变量。
巩固拓展
如下图,一个底面周长为9.42厘米的圆柱体,从中间斜着截去一段后,它的体积是多少?
4厘米
6厘米
想一想,如果把不规则的部分从中间分成两份,在重新拼在一起,能得到一个什么图形?
巩固拓展
如下图,一个底面周长为9.42厘米的圆柱体,从中间斜着截去一段后,它的体积是多少?
从侧面横截面观察
巩固拓展
如下图,一个底面周长为9.42厘米的圆柱体,从中间斜着截去一段后,它的体积是多少?
解法一:
3.14×(9.42÷3.14÷2)2 ×10÷2
=35.325(立方厘米)
解法二:
3.14×(9.42÷3.14÷2)2 ×4+3.14×(9.42÷3.14÷2)2 ×2÷2
=3.14×1.52 ×5
=35.325(立方厘米)
答:它的体积是35.325立方厘米。
巩固拓展
下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
请你想一想,上面4个图形当以长为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试。
图1
图2
图3
图4
巩固拓展
下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
设π=3
图1
图2
图3
图4
图1
半径:18÷3÷2=3(dm)
图2
半径:12÷3÷2=2(dm)
图3
半径:9÷3÷2=1.5(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×3 ×2=54(dm )
体积:3×2 ×3=36(dm )
体积:3×1.5 ×4=27(dm )
体积:3×1 ×6=18(dm )
答:图4圆柱的体积最小,图1圆柱的体积最大。
巩固拓展
下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
图1
图2
图3
图4
我发现,上面4个图形。当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。
课堂小结
求不规则物体的体积或容积,可以利用转化的思想方法,将其转化为规则的图形进行计算。
课后作业
完成课后对应内容。
祝 你 学 习 进 步!
https://www.21cnjy.com/help/help_extract.php
