人教版九年级数学下册26.1. 2反比例函数的图象和性质 课件(共17张PPT)
文档属性
| 名称 | 人教版九年级数学下册26.1. 2反比例函数的图象和性质 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 13:09:49 | ||
图片预览



文档简介
(共17张PPT)
第二十六章 反比例函数
26.1.2 反比例函数的图像和性质
已知一次函数y=kx+b(k≠0)的图象是
反比例函数 (k≠0)的图象是什么呢?
让我们一起画个反比例函数的图象看看,好吗?
x
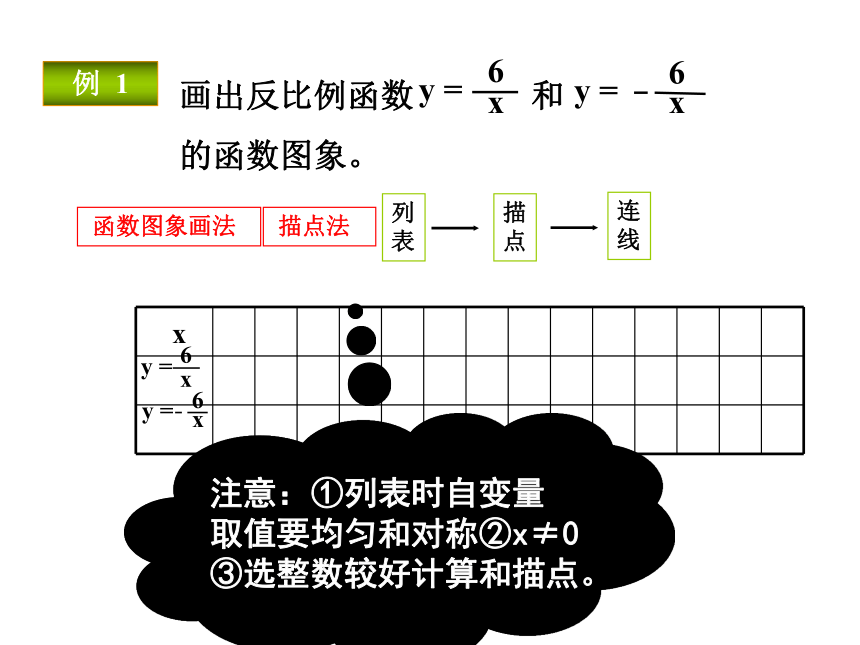
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
函数图象画法
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。
例 1
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
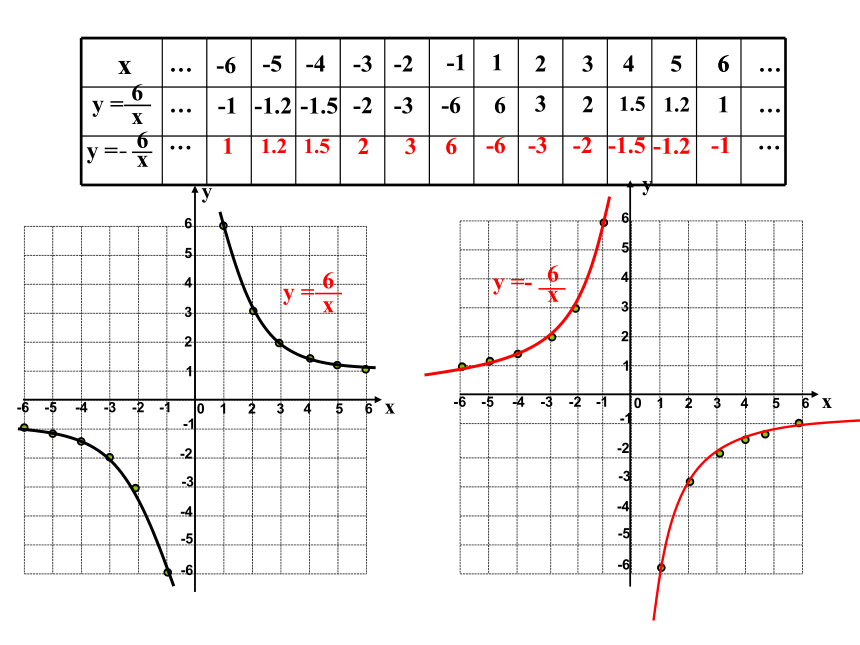
y =
x
6
y =-
x
6
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-5
5
x
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-5
5
x
y =
x
6
y =-
x
6
y
y
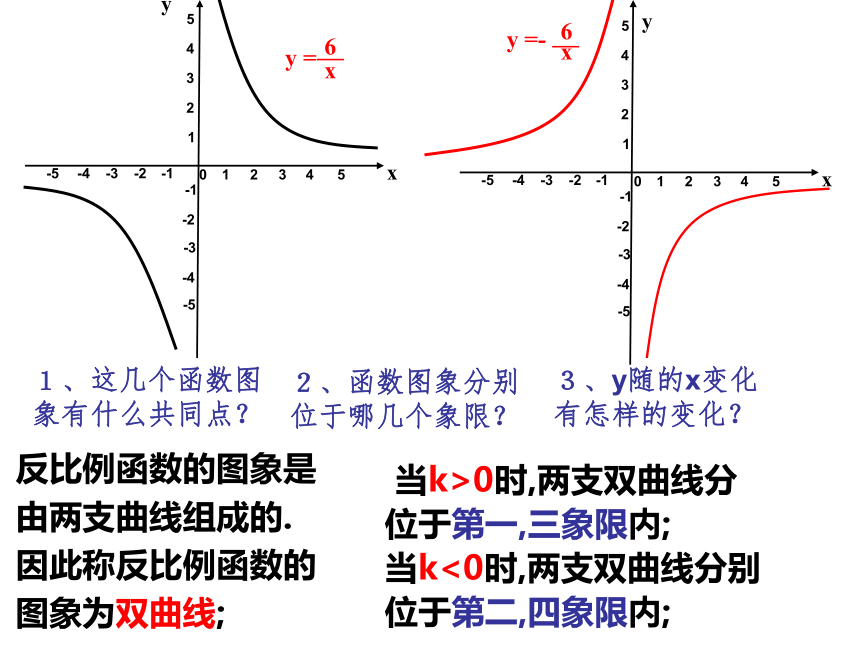
1、这几个函数图象有什么共同点?
2、函数图象分别位于哪几个象限?
3、y随的x变化有怎样的变化?
反比例函数的图象是
由两支曲线组成的.
因此称反比例函数的
图象为双曲线;
当k>0时,两支双曲线分
位于第一,三象限内;
当k<0时,两支双曲线分别
位于第二,四象限内;
由两支曲线组成的.因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
既是中心对称,又是轴对称
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
对称性
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
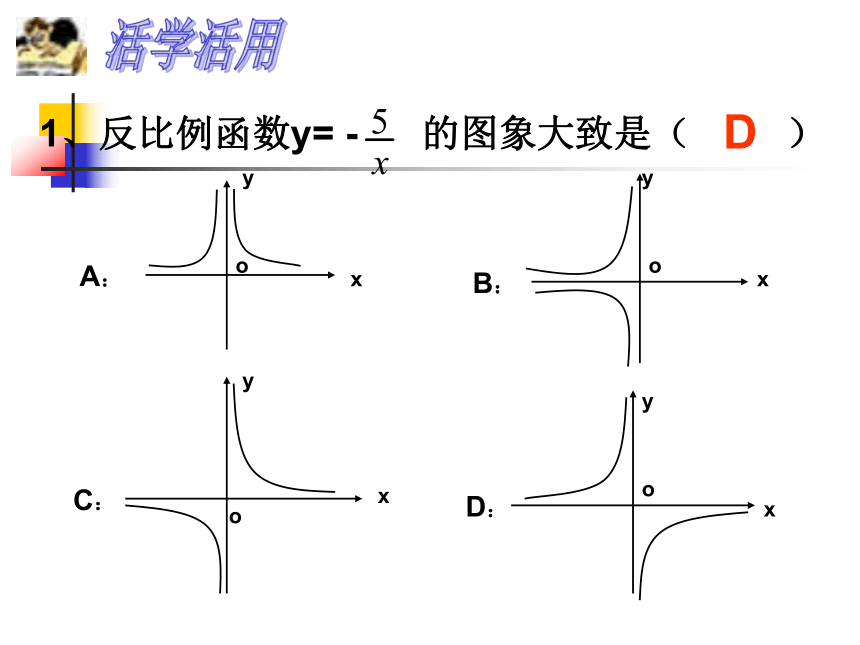
1、反比例函数y= - 的图象大致是( )
D
1、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
练一练
1
已知反比例函数
若A(7,y1),B(5,y2)在函数图象上,
则y1与y2的大小关系是_____________;
(2)若A(-7,y1),B(-5,y2)在函数图象上,
则y1与y2的大小关系是_____________;
(3)若A(7,y1),B(-5,y2)在函数图象上,
则y1与y2的大小关系是_____________;
(4)若A(-7,y1),B(5,y2)在函数图象上,
则y1与y2的大小关系是_____________;
练一练
2
练一练
3
若点(x1,50)、(x2,100)、(x3,-50)在
反比例函数 的图象上,则( )
A、x1>x2>x3 B、x2>x1>x3
C、x3>x1>x2 D、x3>x2>x1
D
已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).
o
(A) (B) (C) (D)
r/cm
h/cm
o
r/cm
h/cm
o
r/cm
h/cm
o
r/cm
h/cm
练一练
5
C
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :
x
y
o
x
y
o
x
y
o
x
y
o
(A) (B) (C) (D)
练一练
6
D
由两支曲线组成的.因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
既是中心对称,又是轴对称
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
对称性
练 习
1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
x
k
2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )
x
k
3.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是( )
(A) y = -5x -1 ( B)y =
(C)y=-2x+2; (D)y=4x.
2
x
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
(A)
x
y
0
x
y
0
(B)
(C)
(D)
x
y
0
x
y
0
D
C
C
1.通过本节课的学习,你有什么收获?还有什么困惑吗?
2.你对自己本节课的表现满意吗?为什么?
数缺形时少直觉,
形少数时难入微.
考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
练一练
5
-1
-1-20
第二十六章 反比例函数
26.1.2 反比例函数的图像和性质
已知一次函数y=kx+b(k≠0)的图象是
反比例函数 (k≠0)的图象是什么呢?
让我们一起画个反比例函数的图象看看,好吗?
x
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
函数图象画法
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。
例 1
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =-
x
6
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-5
5
x
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-5
5
x
y =
x
6
y =-
x
6
y
y
1、这几个函数图象有什么共同点?
2、函数图象分别位于哪几个象限?
3、y随的x变化有怎样的变化?
反比例函数的图象是
由两支曲线组成的.
因此称反比例函数的
图象为双曲线;
当k>0时,两支双曲线分
位于第一,三象限内;
当k<0时,两支双曲线分别
位于第二,四象限内;
由两支曲线组成的.因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
既是中心对称,又是轴对称
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
对称性
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
1、反比例函数y= - 的图象大致是( )
D
1、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
练一练
1
已知反比例函数
若A(7,y1),B(5,y2)在函数图象上,
则y1与y2的大小关系是_____________;
(2)若A(-7,y1),B(-5,y2)在函数图象上,
则y1与y2的大小关系是_____________;
(3)若A(7,y1),B(-5,y2)在函数图象上,
则y1与y2的大小关系是_____________;
(4)若A(-7,y1),B(5,y2)在函数图象上,
则y1与y2的大小关系是_____________;
练一练
2
练一练
3
若点(x1,50)、(x2,100)、(x3,-50)在
反比例函数 的图象上,则( )
A、x1>x2>x3 B、x2>x1>x3
C、x3>x1>x2 D、x3>x2>x1
D
已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).
o
(A) (B) (C) (D)
r/cm
h/cm
o
r/cm
h/cm
o
r/cm
h/cm
o
r/cm
h/cm
练一练
5
C
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :
x
y
o
x
y
o
x
y
o
x
y
o
(A) (B) (C) (D)
练一练
6
D
由两支曲线组成的.因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
既是中心对称,又是轴对称
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
对称性
练 习
1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
x
k
2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )
x
k
3.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是( )
(A) y = -5x -1 ( B)y =
(C)y=-2x+2; (D)y=4x.
2
x
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
(A)
x
y
0
x
y
0
(B)
(C)
(D)
x
y
0
x
y
0
D
C
C
1.通过本节课的学习,你有什么收获?还有什么困惑吗?
2.你对自己本节课的表现满意吗?为什么?
数缺形时少直觉,
形少数时难入微.
考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
练一练
5
-1
-1
