人教版九年级数学下册第28章锐角三角函数复习 课件(共25张PPT)
文档属性
| 名称 | 人教版九年级数学下册第28章锐角三角函数复习 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 08:42:01 | ||
图片预览





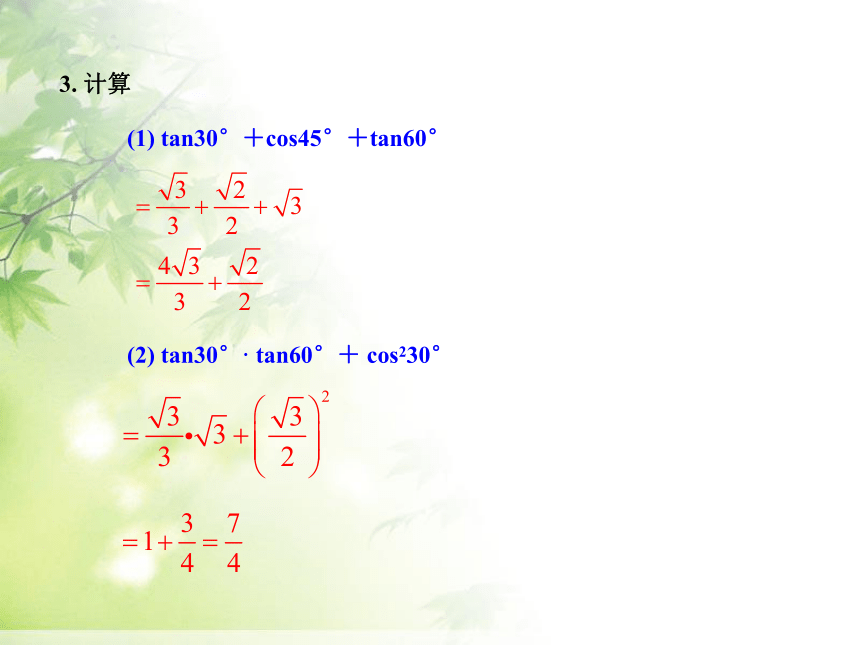
文档简介
(共25张PPT)
《锐角三角函数》复习
学习目标:
1. 认识锐角的正弦、余弦、正切; 知道30°、45°、60°角的三角函数值;会计算含有特殊角的三角函数式的值
2.会解直角三角形;能根据问题的需要合理作出垂线,构造直角三角形;会解两个特殊直角三角形的组合图形
3.会利用直角三角形解决简单的实际问题.
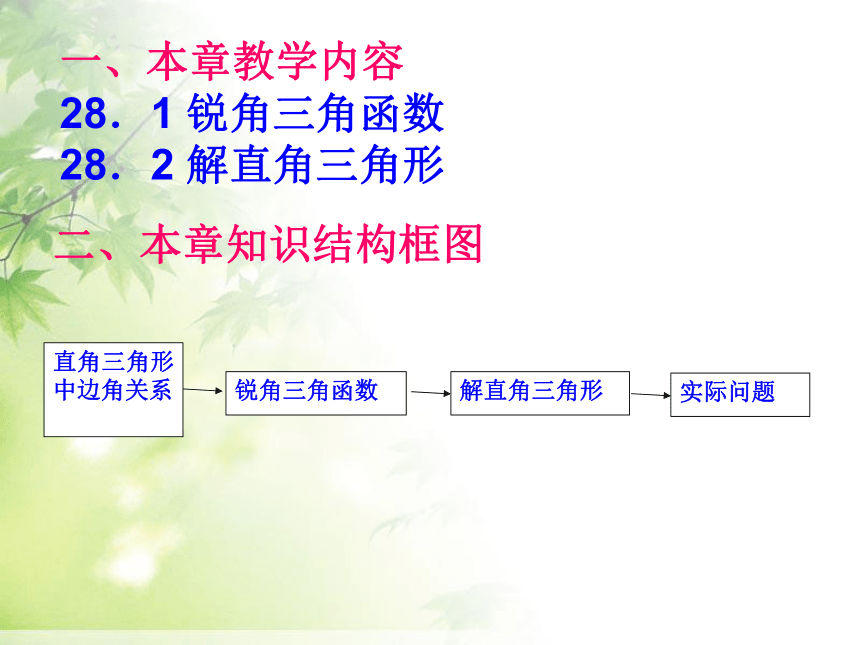
一、本章教学内容
28.1 锐角三角函数
28.2 解直角三角形
二、本章知识结构框图
直角三角形中边角关系
锐角三角函数
解直角三角形
实际问题
1. 结合图,请学生回答:什么是∠A正弦、余弦、正切 ?
A
B
C
b
a
c
在△ABC中,∠C为直角,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作
锐角A的邻边与斜边的比叫做∠ A的余弦,记作
锐角A的对边与邻边的比叫做∠ A的正切,记作
我们把 A的正弦、余弦、正切都叫做∠A的三角函数
三:重点概念回顾
2. 若 且∠B=90°- ∠A,则sinB=____________
3. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB,那么
△ABC一定是____________三角形.
直角
练习巩固
1. 分别求出图中∠A的正弦值、余弦值和正切值
A
C
B
A
C
B
A
C
B
2
6
6
2
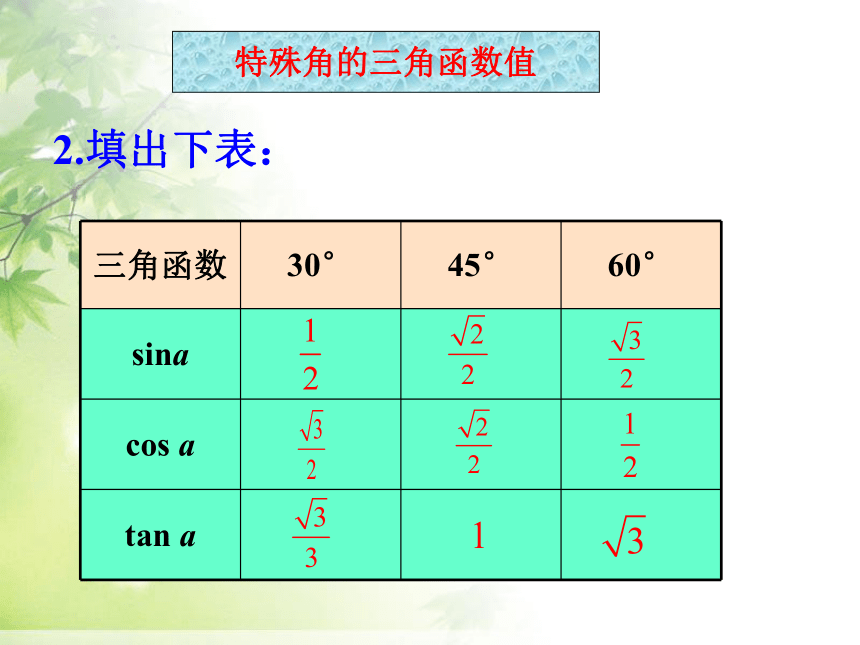
三角函数 30° 45° 60°
sina
cos a
tan a
2.填出下表:
特殊角的三角函数值
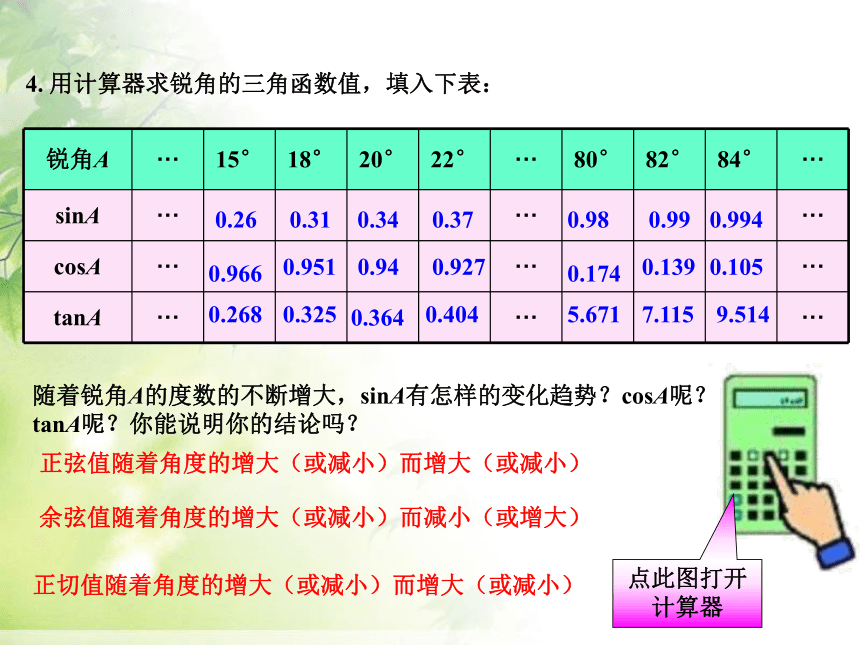
4. 用计算器求锐角的三角函数值,填入下表:
随着锐角A的度数的不断增大,sinA有怎样的变化趋势?cosA呢?tanA呢?你能说明你的结论吗?
锐角A ··· 15° 18° 20° 22° ··· 80° 82° 84° ···
sinA ··· ··· ···
cosA ··· ··· ···
tanA ··· ··· ···
0.26
0.31
0.34
0.37
0.98
0.99
0.994
0.966
0.951
0.94
0.927
0.174
0.139
0.105
0.268
0.325
0.364
0.404
5.671
7.115
9.514
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
点此图打开计算器
1.填空: 若 ,则 α=_______度;若 则α=____________度;若 ,则α=____________度.
60
45
30
练习巩固
2. 选择题,(1)下列等式中,成立的是( )
A. tan45°5′< 1 B. sin29°59′>
C. tan60°1′< D. cos44°48′>
D
(1) tan30°+cos45°+tan60°
(2) tan30°· tan60°+ cos230°
3. 计算
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
3. 解直角三角形
4、解直角三角形的应用
(1)将实际问题化为数学问题;
(画出图形、化为直角三角形问题)
(2)选择适当的三角函数解直角三角形;
(3)将数学答案写为实际问题答案。
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
tan α =
h
l
概念反馈
(1)仰角和俯角
(3)方向角
30°
45°
B
O
A
东
西
北
南
α为坡角
视线
铅垂线
水平线
视线
仰角
俯角
几种基本图形
某人在A处测得建筑物的仰角∠BAC为300 ,沿AC方向行20m至D处,测得仰角∠BDC 为450,求此建筑物的高度BC.
A
C
例 1
B
____________________
D
如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 ,航行24海里到C,见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
C
B
A
N1
D
N
例 2
练习1.国外船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.
P
A
B
练习2.请观察:小山的高为h,为了测的小山顶上铁塔AB的高x,在平地上选择一点P, 在P点处测得B点的仰角为a, A点的仰角为β .(见表中测量目标图)
P
A
B
C
a
β
X
h
题目 测量山顶铁塔的高
测量目标
已知数据
山高BC h=150米
仰角a a=45
仰角β β =30
练习3.某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少 (结果精确到0.01m).
sin350 =0.57, sin400 =0.64
A
B
C
D
┌
4m
350
400
小结:
本节课你学了哪些内容,有何收获
A
B
C
D
1、Rt△BAC中,∠C=900,CA=CB
D是AC上一点,且CA= AC,求∠ABD的三个三角函数值。
E
2、如图,角α的顶点的原点,始边与x正半轴重合,终边上有一点P(x,y)。
O
P
x
y
则OP=
C
则sinα=
cosα=
tanα=
α
3、正弦、正切的值随锐角的增大而增大;
余弦的值随锐角的增大而减少。
1、锐角A>300,则角A的三个三角函数值的取值范围是什么?
4.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
60°
12
30°
590
310
5.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,
求电线杆AB的高.(精确到0.1米)
1.20
22.7
α=22°
E
7.(2007)如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,tan∠PAB= 且O、A、B在同一条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
2
1
A
B
水平地面
C
O
山坡
60°
45°
P
E
《锐角三角函数》复习
学习目标:
1. 认识锐角的正弦、余弦、正切; 知道30°、45°、60°角的三角函数值;会计算含有特殊角的三角函数式的值
2.会解直角三角形;能根据问题的需要合理作出垂线,构造直角三角形;会解两个特殊直角三角形的组合图形
3.会利用直角三角形解决简单的实际问题.
一、本章教学内容
28.1 锐角三角函数
28.2 解直角三角形
二、本章知识结构框图
直角三角形中边角关系
锐角三角函数
解直角三角形
实际问题
1. 结合图,请学生回答:什么是∠A正弦、余弦、正切 ?
A
B
C
b
a
c
在△ABC中,∠C为直角,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作
锐角A的邻边与斜边的比叫做∠ A的余弦,记作
锐角A的对边与邻边的比叫做∠ A的正切,记作
我们把 A的正弦、余弦、正切都叫做∠A的三角函数
三:重点概念回顾
2. 若 且∠B=90°- ∠A,则sinB=____________
3. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB,那么
△ABC一定是____________三角形.
直角
练习巩固
1. 分别求出图中∠A的正弦值、余弦值和正切值
A
C
B
A
C
B
A
C
B
2
6
6
2
三角函数 30° 45° 60°
sina
cos a
tan a
2.填出下表:
特殊角的三角函数值
4. 用计算器求锐角的三角函数值,填入下表:
随着锐角A的度数的不断增大,sinA有怎样的变化趋势?cosA呢?tanA呢?你能说明你的结论吗?
锐角A ··· 15° 18° 20° 22° ··· 80° 82° 84° ···
sinA ··· ··· ···
cosA ··· ··· ···
tanA ··· ··· ···
0.26
0.31
0.34
0.37
0.98
0.99
0.994
0.966
0.951
0.94
0.927
0.174
0.139
0.105
0.268
0.325
0.364
0.404
5.671
7.115
9.514
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
点此图打开计算器
1.填空: 若 ,则 α=_______度;若 则α=____________度;若 ,则α=____________度.
60
45
30
练习巩固
2. 选择题,(1)下列等式中,成立的是( )
A. tan45°5′< 1 B. sin29°59′>
C. tan60°1′< D. cos44°48′>
D
(1) tan30°+cos45°+tan60°
(2) tan30°· tan60°+ cos230°
3. 计算
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
3. 解直角三角形
4、解直角三角形的应用
(1)将实际问题化为数学问题;
(画出图形、化为直角三角形问题)
(2)选择适当的三角函数解直角三角形;
(3)将数学答案写为实际问题答案。
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
tan α =
h
l
概念反馈
(1)仰角和俯角
(3)方向角
30°
45°
B
O
A
东
西
北
南
α为坡角
视线
铅垂线
水平线
视线
仰角
俯角
几种基本图形
某人在A处测得建筑物的仰角∠BAC为300 ,沿AC方向行20m至D处,测得仰角∠BDC 为450,求此建筑物的高度BC.
A
C
例 1
B
____________________
D
如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 ,航行24海里到C,见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
C
B
A
N1
D
N
例 2
练习1.国外船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.
P
A
B
练习2.请观察:小山的高为h,为了测的小山顶上铁塔AB的高x,在平地上选择一点P, 在P点处测得B点的仰角为a, A点的仰角为β .(见表中测量目标图)
P
A
B
C
a
β
X
h
题目 测量山顶铁塔的高
测量目标
已知数据
山高BC h=150米
仰角a a=45
仰角β β =30
练习3.某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少 (结果精确到0.01m).
sin350 =0.57, sin400 =0.64
A
B
C
D
┌
4m
350
400
小结:
本节课你学了哪些内容,有何收获
A
B
C
D
1、Rt△BAC中,∠C=900,CA=CB
D是AC上一点,且CA= AC,求∠ABD的三个三角函数值。
E
2、如图,角α的顶点的原点,始边与x正半轴重合,终边上有一点P(x,y)。
O
P
x
y
则OP=
C
则sinα=
cosα=
tanα=
α
3、正弦、正切的值随锐角的增大而增大;
余弦的值随锐角的增大而减少。
1、锐角A>300,则角A的三个三角函数值的取值范围是什么?
4.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
60°
12
30°
590
310
5.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,
求电线杆AB的高.(精确到0.1米)
1.20
22.7
α=22°
E
7.(2007)如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,tan∠PAB= 且O、A、B在同一条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
2
1
A
B
水平地面
C
O
山坡
60°
45°
P
E
