人教版数学六年级下册3.6 圆锥的体积 课件(共22张PPT)
文档属性
| 名称 | 人教版数学六年级下册3.6 圆锥的体积 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 20:58:54 | ||
图片预览






文档简介
(共22张PPT)
2022年春人教版数学
六年级下册数学精品课件
《圆柱与圆锥》
第六课时 圆锥的体积
小学数学
复习旧知
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
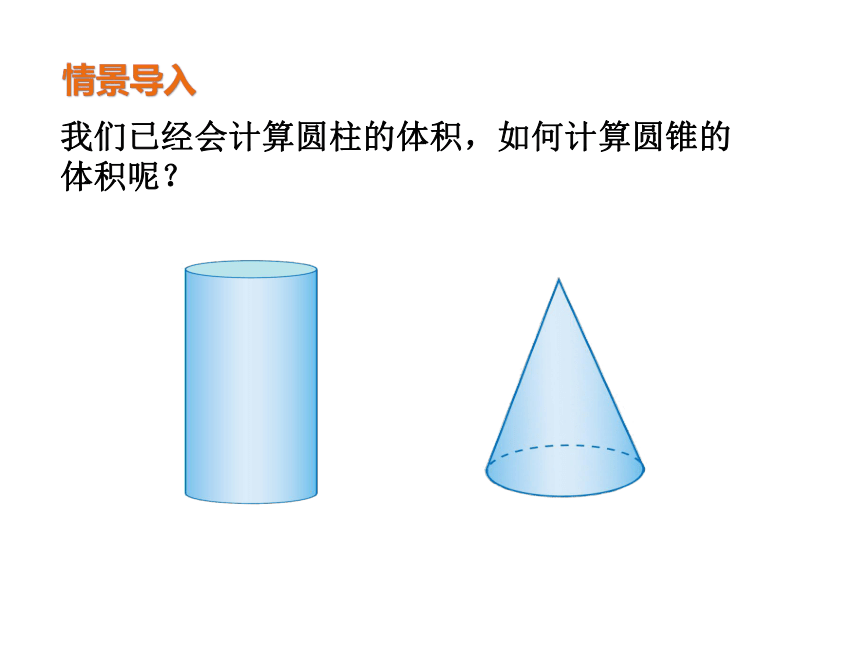
情景导入
我们已经会计算圆柱的体积,如何计算圆锥的体积呢?
探究新知
圆锥的体积和圆柱的体积有没有关系呢?
圆柱的底面是圆,圆锥的底面也是圆……
可以通过试验,探究一下圆锥和圆柱体积之间的关系……
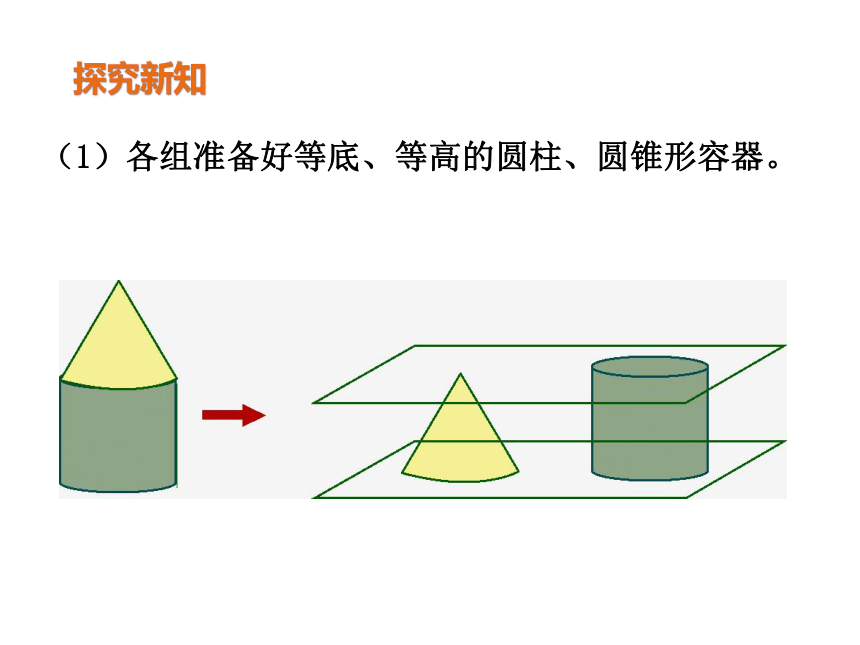
探究新知
(1)各组准备好等底、等高的圆柱、圆锥形容器。
探究新知
(2)用倒沙子或水的方法试一试。
我把圆柱装满水,再往圆锥里倒。
我把圆柱装满沙子,再往圆锥里倒。
正好倒了三次。
三次正好装满。
探究新知
(3)通过试验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
圆柱的体积等于三个和它等底等高的圆锥的体积……
V圆锥= V圆柱= Sh= r2h
1
3
1
3
1
3
探究新知
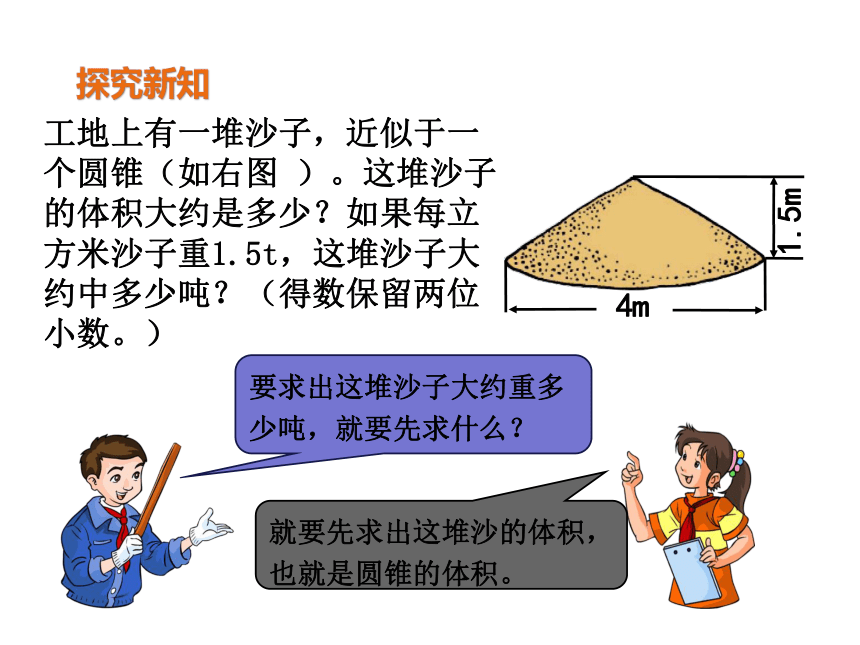
工地上有一堆沙子,近似于一个圆锥(如右图 )。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约中多少吨?(得数保留两位小数。)
4m
1.5m
要求出这堆沙子大约重多少吨,就要先求什么?
就要先求出这堆沙的体积,也就是圆锥的体积。
探究新知
工地上有一堆沙子,近似于一个圆锥(如右图 )。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约中多少吨?(得数保留两位小数。)
4m
1.5m
(2)沙堆的体积:
(1)沙堆底面积:
5.02×1.5=7.53(t)
(3)沙堆重:
答:这堆沙子大约重7.53吨。
×12.56×1.2=5.024≈5.02(m )
3.14 ×( )2=3.14×4=12.56(m2)
1
3
4
2
探究新知
一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm 。
×19 ×12=76(cm )
3
1
探究新知
一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数)
(2)铅锤的体积:
(1)铅锤底面积:
21×7.8≈163(g)
(3)铅锤的质量:
答:这个铅锤大约重163克 。
×12.56×5≈21(cm3)
3.14×( )2=3.14×4=12.56(cm2)
4
2
1
3
易错举例
圆柱的体积是圆锥体积的3倍。
×
这种说法是错误的。
这种说法忽略了“等底等高”这个前提。不是任意两个圆柱和圆锥之间都存在“3倍”或“ ”的关系。
温馨提示:只有等底等高的圆柱和圆锥的体积一定存在3倍的关系。
1
3
正确解答:
×3.14×(5÷2)2×4
= ×19.625×4
≈26.17(dm3)
答:圆锥的体积约是26.17dm3。
1
3
1
3
解得不对。
这道题错在求圆锥的体积时只用它的底面积乘高,而没有乘 。
温馨提示:运用圆锥公式求体积时不要忘记乘 。
1
3
1
3
易错举例
一个圆锥的底面直径是5dm,高是4dm,求圆锥的体积。
3.14×(5÷2)2×4
=3.14×6.25×4
=78.5(dm3)
答:圆锥的体积是78.5(dm3)
解得对吗?
×
巩固拓展
求下面圆锥的体积。
(1)底面的面积是120 cm2,高是15 cm。
(2)底面半径是6 cm,高是10 cm。
(1) 120×15×
= 120×5
= 600(cm3)
1
3
(2) 3.14×62×10×
= 3.14×120
= 376.8(cm3)
1
3
巩固拓展
如图,把圆柱削成一个最大的圆锥。削去部分的体积是多少立方厘米?
10cm
15cm
3.14×(10÷2)2×15×
=3.14×25×15×
=785(cm3)
答:削去部分的体积是785cm3。
3
2
3
2
一个圆锥的底面直径是8cm,从圆锥的顶点沿着高将它切成相等的两半后,表面积比原来的圆锥增加了48cm .这个圆锥的体积是多少cm
巩固拓展
(48÷2)×2÷8=6(cm)
8÷2=4(cm)
×3.14×4 ×6
= ×3.14×16×6
=100.48(cm )
答:这个圆锥的体积是100.48cm 。
1
3
1
3
课堂小结
圆锥体积的计算公式:圆锥的体积=底面积×高× 。如果用S表示圆锥的底面积,用h表示圆锥的高,用r表示圆锥的底面半径,则圆锥体积的计算公式为V= Sh或V= r2h。
1
3
1
3
1
3
课后作业
完成课后对应内容。
祝 你 学 习 进 步!
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
六年级下册数学精品课件
《圆柱与圆锥》
第六课时 圆锥的体积
小学数学
复习旧知
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
情景导入
我们已经会计算圆柱的体积,如何计算圆锥的体积呢?
探究新知
圆锥的体积和圆柱的体积有没有关系呢?
圆柱的底面是圆,圆锥的底面也是圆……
可以通过试验,探究一下圆锥和圆柱体积之间的关系……
探究新知
(1)各组准备好等底、等高的圆柱、圆锥形容器。
探究新知
(2)用倒沙子或水的方法试一试。
我把圆柱装满水,再往圆锥里倒。
我把圆柱装满沙子,再往圆锥里倒。
正好倒了三次。
三次正好装满。
探究新知
(3)通过试验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
圆柱的体积等于三个和它等底等高的圆锥的体积……
V圆锥= V圆柱= Sh= r2h
1
3
1
3
1
3
探究新知
工地上有一堆沙子,近似于一个圆锥(如右图 )。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约中多少吨?(得数保留两位小数。)
4m
1.5m
要求出这堆沙子大约重多少吨,就要先求什么?
就要先求出这堆沙的体积,也就是圆锥的体积。
探究新知
工地上有一堆沙子,近似于一个圆锥(如右图 )。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约中多少吨?(得数保留两位小数。)
4m
1.5m
(2)沙堆的体积:
(1)沙堆底面积:
5.02×1.5=7.53(t)
(3)沙堆重:
答:这堆沙子大约重7.53吨。
×12.56×1.2=5.024≈5.02(m )
3.14 ×( )2=3.14×4=12.56(m2)
1
3
4
2
探究新知
一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm 。
×19 ×12=76(cm )
3
1
探究新知
一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数)
(2)铅锤的体积:
(1)铅锤底面积:
21×7.8≈163(g)
(3)铅锤的质量:
答:这个铅锤大约重163克 。
×12.56×5≈21(cm3)
3.14×( )2=3.14×4=12.56(cm2)
4
2
1
3
易错举例
圆柱的体积是圆锥体积的3倍。
×
这种说法是错误的。
这种说法忽略了“等底等高”这个前提。不是任意两个圆柱和圆锥之间都存在“3倍”或“ ”的关系。
温馨提示:只有等底等高的圆柱和圆锥的体积一定存在3倍的关系。
1
3
正确解答:
×3.14×(5÷2)2×4
= ×19.625×4
≈26.17(dm3)
答:圆锥的体积约是26.17dm3。
1
3
1
3
解得不对。
这道题错在求圆锥的体积时只用它的底面积乘高,而没有乘 。
温馨提示:运用圆锥公式求体积时不要忘记乘 。
1
3
1
3
易错举例
一个圆锥的底面直径是5dm,高是4dm,求圆锥的体积。
3.14×(5÷2)2×4
=3.14×6.25×4
=78.5(dm3)
答:圆锥的体积是78.5(dm3)
解得对吗?
×
巩固拓展
求下面圆锥的体积。
(1)底面的面积是120 cm2,高是15 cm。
(2)底面半径是6 cm,高是10 cm。
(1) 120×15×
= 120×5
= 600(cm3)
1
3
(2) 3.14×62×10×
= 3.14×120
= 376.8(cm3)
1
3
巩固拓展
如图,把圆柱削成一个最大的圆锥。削去部分的体积是多少立方厘米?
10cm
15cm
3.14×(10÷2)2×15×
=3.14×25×15×
=785(cm3)
答:削去部分的体积是785cm3。
3
2
3
2
一个圆锥的底面直径是8cm,从圆锥的顶点沿着高将它切成相等的两半后,表面积比原来的圆锥增加了48cm .这个圆锥的体积是多少cm
巩固拓展
(48÷2)×2÷8=6(cm)
8÷2=4(cm)
×3.14×4 ×6
= ×3.14×16×6
=100.48(cm )
答:这个圆锥的体积是100.48cm 。
1
3
1
3
课堂小结
圆锥体积的计算公式:圆锥的体积=底面积×高× 。如果用S表示圆锥的底面积,用h表示圆锥的高,用r表示圆锥的底面半径,则圆锥体积的计算公式为V= Sh或V= r2h。
1
3
1
3
1
3
课后作业
完成课后对应内容。
祝 你 学 习 进 步!
https://www.21cnjy.com/help/help_extract.php
