人教版七年级下册数学同步课时作业 5.1.1 相交线(含答案)
文档属性
| 名称 | 人教版七年级下册数学同步课时作业 5.1.1 相交线(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 13:21:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版七年级下册数学同步课时作业
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
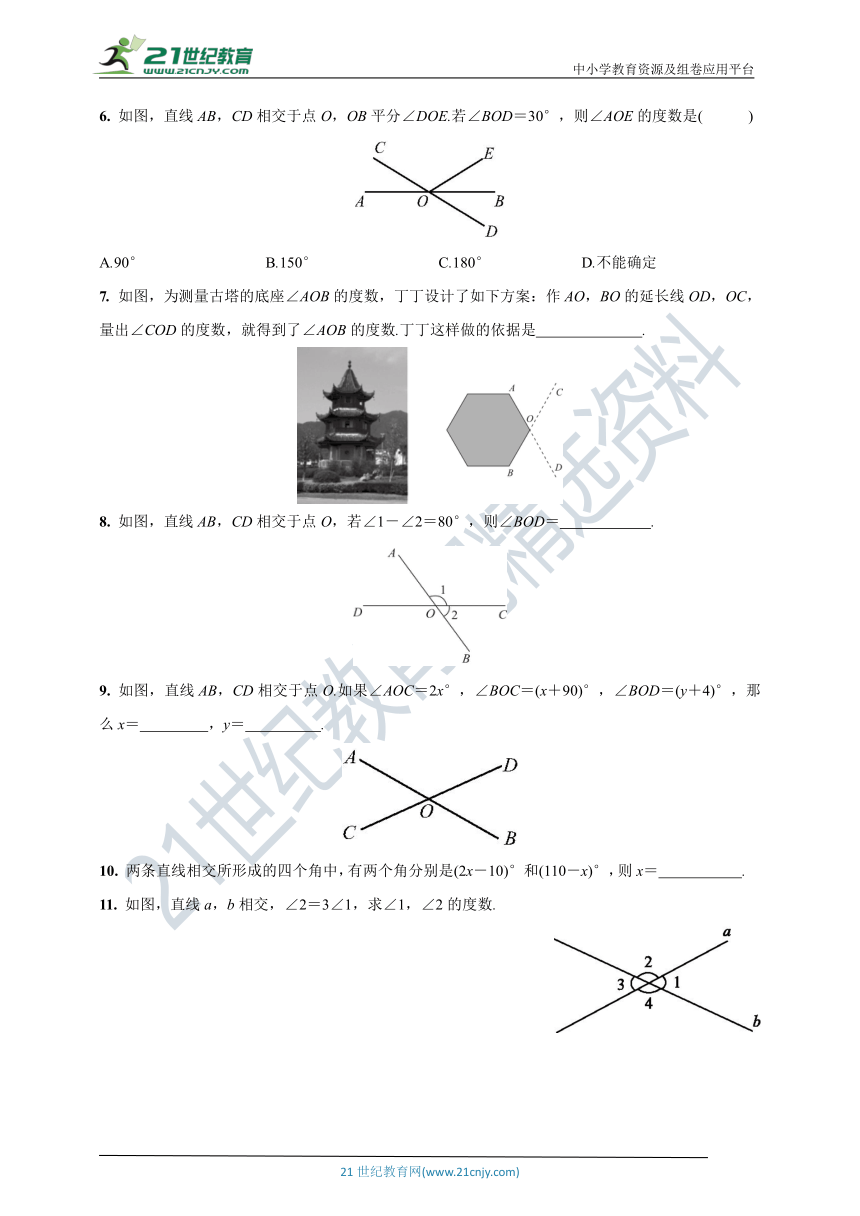
1. 下列选项中,∠1与∠2是邻补角的是( )
A B C D
2. 如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5
3. 如图,直线AB,CD相交于点O,∠1=∠2,∠3=120°,则∠COE的度数是( )
A.70° B.65° C.60° D.50°
4. 如图,直线AB,CD相交于点O,若∠AOC+∠BOD=140°,则∠AOC的度数为( )
A.40° B.70° C.110° D.140°
5. 平面上五条直线相交于一点,则能构成的对顶角的对数是( )
A.5 B.10 C.20 D.40
6. 如图,直线AB,CD相交于点O,OB平分∠DOE.若∠BOD=30°,则∠AOE的度数是( )
A.90° B.150° C.180° D.不能确定
7. 如图,为测量古塔的底座∠AOB的度数,丁丁设计了如下方案:作AO,BO的延长线OD,OC,量出∠COD的度数,就得到了∠AOB的度数.丁丁这样做的依据是 .
8. 如图,直线AB,CD相交于点O,若∠1-∠2=80°,则∠BOD= .
9. 如图,直线AB,CD相交于点O.如果∠AOC=2x°,∠BOC=(x+90)°,∠BOD=(y+4)°,那么x= ,y= .
10. 两条直线相交所形成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则x= .
11. 如图,直线a,b相交,∠2=3∠1,求∠1,∠2的度数.
12. 如图,直线AB,CD,EF相交于点O,三个交角的关系是∠3=3∠2,∠2=2∠1.求∠1,∠2,∠3的大小.
13. 如图,直线AB,CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(1)求∠AON的度数;
(2)求∠DON的邻补角的度数.
14. 如图,直线AB,CD相交于点O,OM平分∠AOB.
(1)若∠1=∠2,求∠DON的度数;
(2)若∠BOC=4∠1,求∠AOC与∠DOM的度数.
15. 如图,直线AB,CD相交于点E,∠BEC=45°,射线EG在∠AEC内(如图1).
(1)若∠CEG比∠AEG小25°,求∠BEG的大小;
(2)若射线EF平分∠AED,∠FEG=m°(m>90)(如图2),则∠AEG-∠CEG= .(用含m的式子表示,请直接写出结果)
图1 图2
参 考 答 案
1. D 2. A 3. C 4. B 5. C 6. B
7. 对顶角相等
8. 130°
9. 30 56
10. 40或80
11. 解:因为∠2=3∠1,∠1+∠2=180°,所以4∠1=180°,所以∠1=45°,所以∠2=3∠1=135°.
12. 解:设∠1=x°,可得∠2=2∠1=2x°,∠3=3∠2=6x°.因为∠2=∠FOD,∠1+∠FOD+∠3=180°,所以x+2x+6x=180,解得x=20,所以∠1=20°,∠2=40°,∠3=120°.
13. 解:(1)因为∠AOC与∠BOD是对顶角,所以∠BOD=∠AOC=50°.因为OM平分∠BOD,所以∠BOM=∠DOM=∠BOD=25°,所以∠AON=180°-∠MON-∠BOM=180°-90°-25°=65°.
(2)∠DON的邻补角是∠CON,∠CON=∠AON+∠AOC=65°+50°=115°.
14. 解:(1)因为OM平分∠AOB,所以∠1+∠AOC=90°.因为∠1=∠2,所以∠2+∠AOC=90°,所以∠DON=180°-90°=90°.(2)因为∠BOC=4∠1,所以90°+∠1=4∠1,所以∠1=30°,所以∠AOC=90°-30°=60°,∠DOM=180°-30°=150°.
15. 解:(1)由题意可知∠CEG=∠AEG-25°,所以∠BEC+∠CEG+∠AEG=45°+(∠AEG-25°)+∠AEG=180°,解得∠AEG=80°,所以∠BEG=180°-∠AEG=100°.
(2)(2m-180)° 提示:因为EF平分∠AED,∠AED=∠BEC=45°,所以∠AEF=∠DEF=22.5,所以∠AEG=∠FEG-∠AEF=(m-22.5)°,∠CEG=180°-∠FEG-∠DEF=180°-(m+22.5)°,所以∠AEG-∠CEG=(m-22.5)°-(180-m-22.5)°=(2m-180)°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版七年级下册数学同步课时作业
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
1. 下列选项中,∠1与∠2是邻补角的是( )
A B C D
2. 如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5
3. 如图,直线AB,CD相交于点O,∠1=∠2,∠3=120°,则∠COE的度数是( )
A.70° B.65° C.60° D.50°
4. 如图,直线AB,CD相交于点O,若∠AOC+∠BOD=140°,则∠AOC的度数为( )
A.40° B.70° C.110° D.140°
5. 平面上五条直线相交于一点,则能构成的对顶角的对数是( )
A.5 B.10 C.20 D.40
6. 如图,直线AB,CD相交于点O,OB平分∠DOE.若∠BOD=30°,则∠AOE的度数是( )
A.90° B.150° C.180° D.不能确定
7. 如图,为测量古塔的底座∠AOB的度数,丁丁设计了如下方案:作AO,BO的延长线OD,OC,量出∠COD的度数,就得到了∠AOB的度数.丁丁这样做的依据是 .
8. 如图,直线AB,CD相交于点O,若∠1-∠2=80°,则∠BOD= .
9. 如图,直线AB,CD相交于点O.如果∠AOC=2x°,∠BOC=(x+90)°,∠BOD=(y+4)°,那么x= ,y= .
10. 两条直线相交所形成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则x= .
11. 如图,直线a,b相交,∠2=3∠1,求∠1,∠2的度数.
12. 如图,直线AB,CD,EF相交于点O,三个交角的关系是∠3=3∠2,∠2=2∠1.求∠1,∠2,∠3的大小.
13. 如图,直线AB,CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(1)求∠AON的度数;
(2)求∠DON的邻补角的度数.
14. 如图,直线AB,CD相交于点O,OM平分∠AOB.
(1)若∠1=∠2,求∠DON的度数;
(2)若∠BOC=4∠1,求∠AOC与∠DOM的度数.
15. 如图,直线AB,CD相交于点E,∠BEC=45°,射线EG在∠AEC内(如图1).
(1)若∠CEG比∠AEG小25°,求∠BEG的大小;
(2)若射线EF平分∠AED,∠FEG=m°(m>90)(如图2),则∠AEG-∠CEG= .(用含m的式子表示,请直接写出结果)
图1 图2
参 考 答 案
1. D 2. A 3. C 4. B 5. C 6. B
7. 对顶角相等
8. 130°
9. 30 56
10. 40或80
11. 解:因为∠2=3∠1,∠1+∠2=180°,所以4∠1=180°,所以∠1=45°,所以∠2=3∠1=135°.
12. 解:设∠1=x°,可得∠2=2∠1=2x°,∠3=3∠2=6x°.因为∠2=∠FOD,∠1+∠FOD+∠3=180°,所以x+2x+6x=180,解得x=20,所以∠1=20°,∠2=40°,∠3=120°.
13. 解:(1)因为∠AOC与∠BOD是对顶角,所以∠BOD=∠AOC=50°.因为OM平分∠BOD,所以∠BOM=∠DOM=∠BOD=25°,所以∠AON=180°-∠MON-∠BOM=180°-90°-25°=65°.
(2)∠DON的邻补角是∠CON,∠CON=∠AON+∠AOC=65°+50°=115°.
14. 解:(1)因为OM平分∠AOB,所以∠1+∠AOC=90°.因为∠1=∠2,所以∠2+∠AOC=90°,所以∠DON=180°-90°=90°.(2)因为∠BOC=4∠1,所以90°+∠1=4∠1,所以∠1=30°,所以∠AOC=90°-30°=60°,∠DOM=180°-30°=150°.
15. 解:(1)由题意可知∠CEG=∠AEG-25°,所以∠BEC+∠CEG+∠AEG=45°+(∠AEG-25°)+∠AEG=180°,解得∠AEG=80°,所以∠BEG=180°-∠AEG=100°.
(2)(2m-180)° 提示:因为EF平分∠AED,∠AED=∠BEC=45°,所以∠AEF=∠DEF=22.5,所以∠AEG=∠FEG-∠AEF=(m-22.5)°,∠CEG=180°-∠FEG-∠DEF=180°-(m+22.5)°,所以∠AEG-∠CEG=(m-22.5)°-(180-m-22.5)°=(2m-180)°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
