2021-2022学年人教版数学八年级下册19.2.1正比例函数(2)课件(25张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册19.2.1正比例函数(2)课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 25.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 20:49:43 | ||
图片预览






文档简介
(共25张PPT)
19.2.1正比例函数(2)
人教版八年级下册
第19章一次函数
01
理解正比例函数的图象的特点,会利用两点(法)画正比例函数的图象.
02
掌握正比例函数的性质,并能灵活运用解答有关问题.
教学目标
复习回顾
正比例函数
一般地,形如 y=kx(k 是常数,k≠0)的函数,叫做正比例函数,其中 k 叫做比例系数.
(1)正比例函数必须满足两个条件:①比例系数k是常数,且k≠0.②两个变量x、y的次数都是1.
复习回顾
问题2:描点法画函数图象的三个步骤是
_______、_______、_______.
列表
描点
连线
问题1:下列函数哪些是正比例函数?
①y=-3x ; ②y= x + 3;
③y= 4x; ④y= x2.
正比例函数有:①③
新知探究
解: (1)函数y=2x中自变量x可为任意实数.
①列表如下:
问题: 画出下列正比例函数的图象:
(1) y=2x, ; (2) y=-1.5x,y=-4x.
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
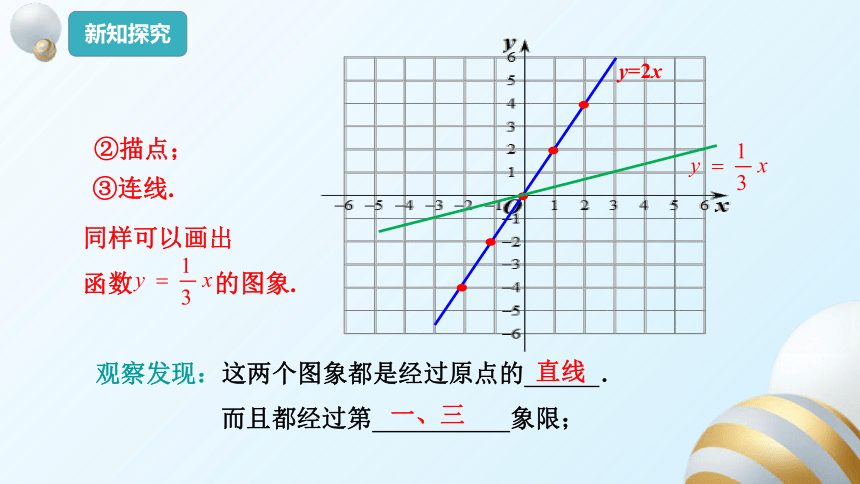
新知探究
y=2x
②描点;
③连线.
同样可以画出
函数 的图象.
观察发现:这两个图象都是经过原点的 .
而且都经过第 象限;
一、三
直线
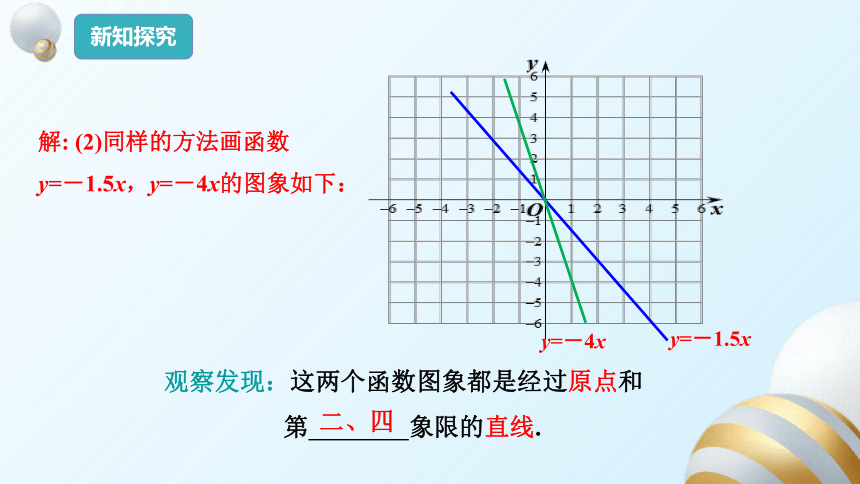
新知探究
解: (2)同样的方法画函数
y=-1.5x,y=-4x的图象如下:
y=-4x
y=-1.5x
观察发现:这两个函数图象都是经过原点和
第 象限的直线.
二、四
新知探究
要点归纳
y=kx (k是常数,k≠0)的图象是一条经过原点的直线
y=kx(k≠0) 经过的象限
k>0 第一、三象限
k<0 第二、四象限
另外:函数y=kx 的图象我们也称作直线y=kx
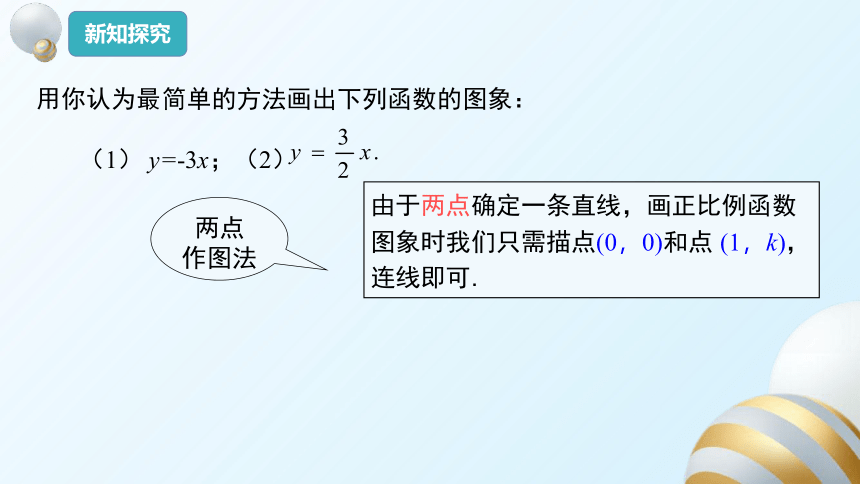
新知探究
用你认为最简单的方法画出下列函数的图象:
(1) y=-3x;(2)
怎样画正比例函数的图象最简单?为什么?
由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.
两点
作图法
新知探究
O
x 0 1
y=-3x
0
-3
0
y=-3x
函数y=-3x, 的图象如下:
解:列表如下:
新知应用
1.正比例函数的图象大致是( )
A. B.
C. D.
B
新知应用
2.函数y=3x的图象经过( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
A
3.一次函数y=2x的图象是( )
A.线段 B.抛物线 C.直线 D.折线
C
新知探究
(1)若函数图象经过第一、三象限,则k的取值
范围是________.
问题: 已知正比例函数y=(k+1)x.
k>-1
解析:因为函数图象经过第一、三象限,所以k+1>0,解得k>-1.
新知探究
(2)若函数图象经过点(2,4),则k_____.
解析:将坐标(2,4)带入函数解析式中,得4=(k+1)·2,解得k=1.
=1
新知应用
问题:在函数y=x , y=3x, y=- x和 y=-4x 中,随着x的增大,y的值分别如何变化
分析:对于函数y=x,当x=-1时,y= ;当x=1时,y= ;当x=2时,y= ;不难发现y的值随x的增大而 .
-1
1
2
增大
新知应用
我们还可以借助函数图象分析此问题.
观察图象可以发现: 直线y=x,y=3x向右逐渐 ,
即y的值随x的增大而增大;
直线y=- x,y=-4x向右逐渐 ,即y的值随x的增大而增大而减小.
上升
下降
归纳总结
在正比例函数y=kx中:图象:经过原点的直线.
当k>0时,图像经过第一、三象限,y的值随着x值的增大而增大;
当k<0时,图像经过第二、四象限,y的值随着x值的增大而减小.
新知应用
C
新知应用
B
新知应用
C
C
课堂练习
D
二、四
0
-3
减小
课堂练习
作 业
课堂总结
正比例函数的图象和性质
图象:经过原点的直线.
①当k>0时,经过第一、三象限;
②当k<0时,经过第二、四象限.
性质:①当k>0时,y的值随x值的增大而增大;
②当k<0时,y的值随x值的增大而减小.
反之也一样.
19.2.1正比例函数(2)
人教版八年级下册
第19章一次函数
19.2.1正比例函数(2)
人教版八年级下册
第19章一次函数
01
理解正比例函数的图象的特点,会利用两点(法)画正比例函数的图象.
02
掌握正比例函数的性质,并能灵活运用解答有关问题.
教学目标
复习回顾
正比例函数
一般地,形如 y=kx(k 是常数,k≠0)的函数,叫做正比例函数,其中 k 叫做比例系数.
(1)正比例函数必须满足两个条件:①比例系数k是常数,且k≠0.②两个变量x、y的次数都是1.
复习回顾
问题2:描点法画函数图象的三个步骤是
_______、_______、_______.
列表
描点
连线
问题1:下列函数哪些是正比例函数?
①y=-3x ; ②y= x + 3;
③y= 4x; ④y= x2.
正比例函数有:①③
新知探究
解: (1)函数y=2x中自变量x可为任意实数.
①列表如下:
问题: 画出下列正比例函数的图象:
(1) y=2x, ; (2) y=-1.5x,y=-4x.
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
新知探究
y=2x
②描点;
③连线.
同样可以画出
函数 的图象.
观察发现:这两个图象都是经过原点的 .
而且都经过第 象限;
一、三
直线
新知探究
解: (2)同样的方法画函数
y=-1.5x,y=-4x的图象如下:
y=-4x
y=-1.5x
观察发现:这两个函数图象都是经过原点和
第 象限的直线.
二、四
新知探究
要点归纳
y=kx (k是常数,k≠0)的图象是一条经过原点的直线
y=kx(k≠0) 经过的象限
k>0 第一、三象限
k<0 第二、四象限
另外:函数y=kx 的图象我们也称作直线y=kx
新知探究
用你认为最简单的方法画出下列函数的图象:
(1) y=-3x;(2)
怎样画正比例函数的图象最简单?为什么?
由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.
两点
作图法
新知探究
O
x 0 1
y=-3x
0
-3
0
y=-3x
函数y=-3x, 的图象如下:
解:列表如下:
新知应用
1.正比例函数的图象大致是( )
A. B.
C. D.
B
新知应用
2.函数y=3x的图象经过( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
A
3.一次函数y=2x的图象是( )
A.线段 B.抛物线 C.直线 D.折线
C
新知探究
(1)若函数图象经过第一、三象限,则k的取值
范围是________.
问题: 已知正比例函数y=(k+1)x.
k>-1
解析:因为函数图象经过第一、三象限,所以k+1>0,解得k>-1.
新知探究
(2)若函数图象经过点(2,4),则k_____.
解析:将坐标(2,4)带入函数解析式中,得4=(k+1)·2,解得k=1.
=1
新知应用
问题:在函数y=x , y=3x, y=- x和 y=-4x 中,随着x的增大,y的值分别如何变化
分析:对于函数y=x,当x=-1时,y= ;当x=1时,y= ;当x=2时,y= ;不难发现y的值随x的增大而 .
-1
1
2
增大
新知应用
我们还可以借助函数图象分析此问题.
观察图象可以发现: 直线y=x,y=3x向右逐渐 ,
即y的值随x的增大而增大;
直线y=- x,y=-4x向右逐渐 ,即y的值随x的增大而增大而减小.
上升
下降
归纳总结
在正比例函数y=kx中:图象:经过原点的直线.
当k>0时,图像经过第一、三象限,y的值随着x值的增大而增大;
当k<0时,图像经过第二、四象限,y的值随着x值的增大而减小.
新知应用
C
新知应用
B
新知应用
C
C
课堂练习
D
二、四
0
-3
减小
课堂练习
作 业
课堂总结
正比例函数的图象和性质
图象:经过原点的直线.
①当k>0时,经过第一、三象限;
②当k<0时,经过第二、四象限.
性质:①当k>0时,y的值随x值的增大而增大;
②当k<0时,y的值随x值的增大而减小.
反之也一样.
19.2.1正比例函数(2)
人教版八年级下册
第19章一次函数
