人教版六年级下册5 数学广角-鸽巢问题 课件(共24张PPT)
文档属性
| 名称 | 人教版六年级下册5 数学广角-鸽巢问题 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 09:02:19 | ||
图片预览




文档简介
(共24张PPT)
2022年春人教版数学
六年级下册数学精品课件
《第五单元 数学广角》
鸽巢问题
小学数学
情景导入
我给大家表演一个“魔术”。一副牌,取出大小王,还剩52张,你们5人每人随意抽一张,我知道至少有2张牌是同花色的。相信吗?
探究新知
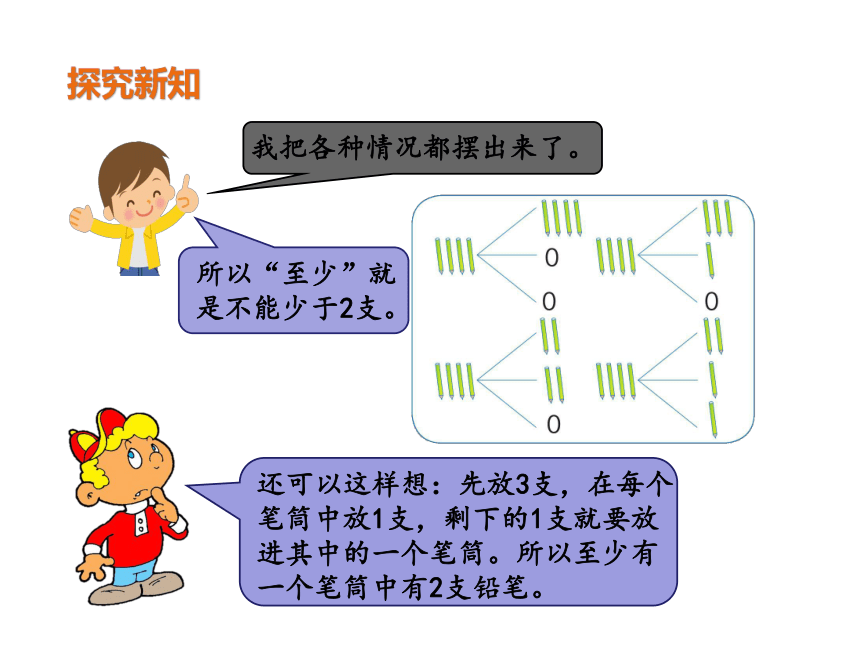
探究新知
我把各种情况都摆出来了。
所以“至少”就是不能少于2支。
还可以这样想:先放3支,在每个笔筒中放1支,剩下的1支就要放进其中的一个笔筒。所以至少有一个笔筒中有2支铅笔。
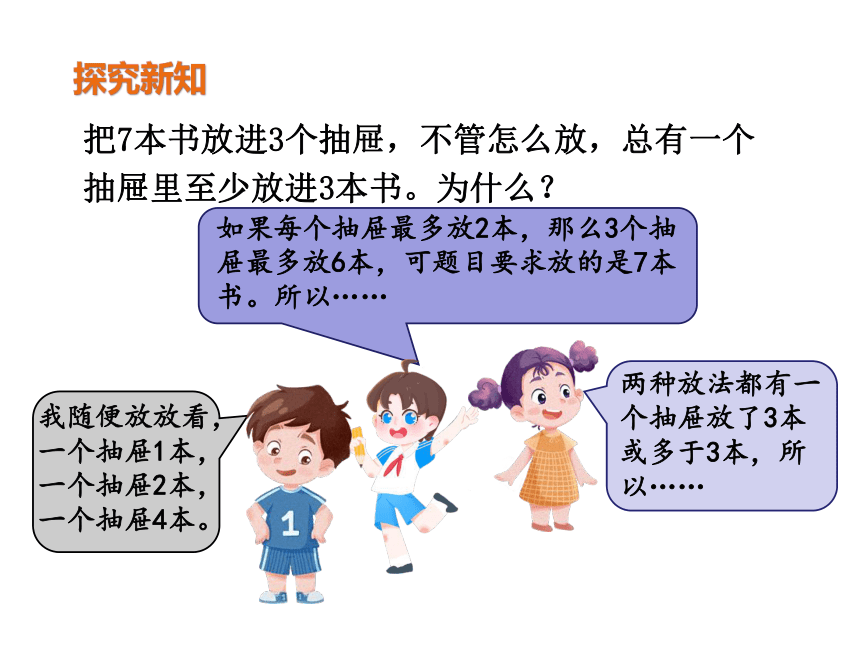
探究新知
把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
如果每个抽屉最多放2本,那么3个抽屉最多放6本,可题目要求放的是7本书。所以……
两种放法都有一个抽屉放了3本或多于3本,所以……
我随便放放看,
一个抽屉1本,
一个抽屉2本,
一个抽屉4本。
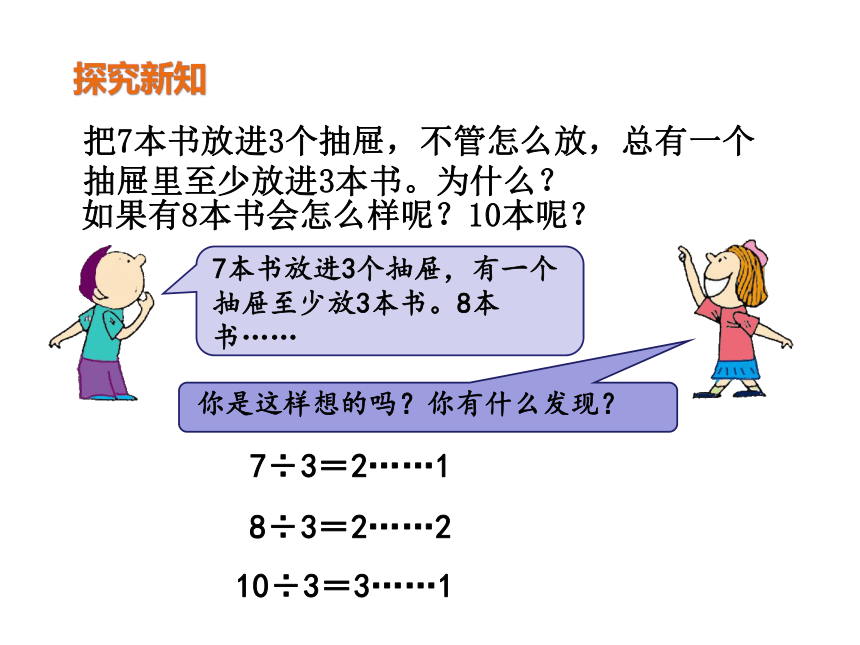
探究新知
把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
如果有8本书会怎么样呢?10本呢?
7本书放进3个抽屉,有一个抽屉至少放3本书。8本书……
你是这样想的吗?你有什么发现?
7÷3=2……1
8÷3=2……2
10÷3=3……1
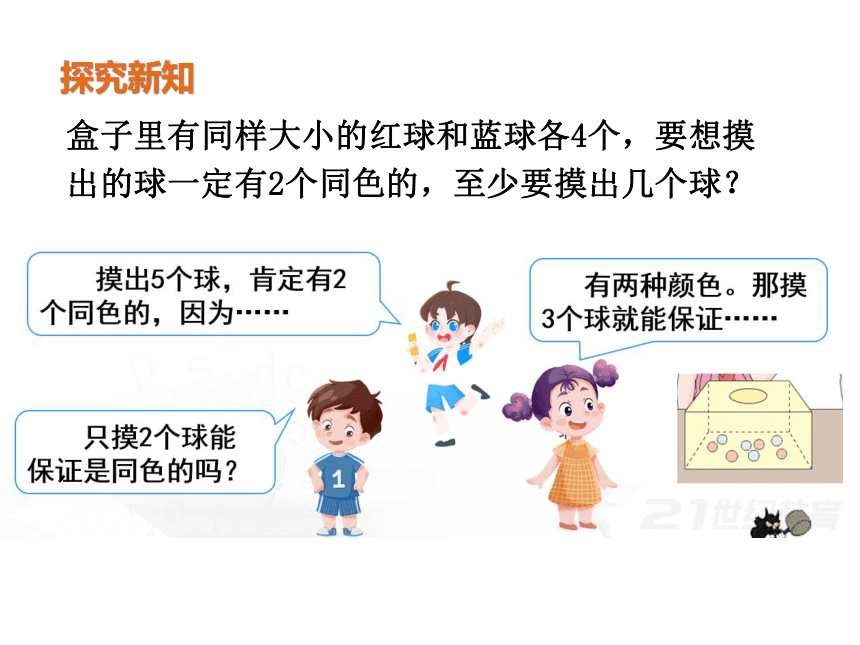
探究新知
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
探究新知
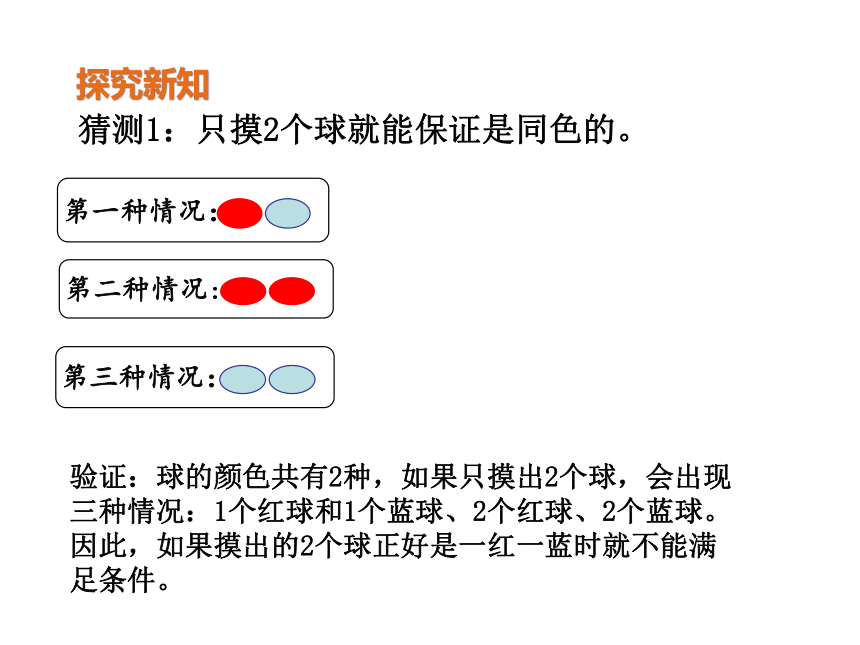
猜测1:只摸2个球就能保证是同色的。
第一种情况:
第二种情况:
第三种情况:
验证:球的颜色共有2种,如果只摸出2个球,会出现三种情况:1个红球和1个蓝球、2个红球、2个蓝球。因此,如果摸出的2个球正好是一红一蓝时就不能满足条件。
探究新知
猜测2:摸出5个球,肯定有2个是同色的。
第一种情况:
第二种情况:
第三种情况:
第四种情况:
验证:把红、蓝两种颜色看成2个“鸽巢”,因为5÷2=2……1,所以摸出5个球时,至少有3个球是同色的,显然,摸出5个球不是最少的。
猜测3:有两种颜色。那摸3个球就能保证有2个同色的球。
第一种情况:
第二种情况:
探究新知
生活中像这样的例子很多,我们能不能把这道题与前面所讲的“鸽巢问题”联系起来进行思考呢?
a.“摸球问题”与“鸽巢问题”有怎样的联系?
b.应该把什么看成“鸽巢”?有几个“鸽巢”?
要分放的东西是什么?
c.得出什么结论?
因为一共有红、蓝两种颜色的球,可以把两种“颜色”看成两个“鸽巢”,“同色”就意味着“同一个鸽巢”。这样,把“摸球问题”转化“鸽巢问题”,即“只要分的物体个数比鸽巢多,就能保证有一个鸽巢至少有两个球”。
探究新知
易错举例
因为11 ÷ 3 = 3……2,所以把11本书放进3个抽屉,总有一个抽屉至少放5本书。
这种说法是错误的。
至少放的书应该是“3(商)+1”,所以应该是4本。
温馨提示:解决此类题时要用商加1,而不是商加余数
×
这种说法是错误的。
至少放的书应该是“3(商)+1”,所以应该是4本。
温馨提示:解决此类题时要用商加1,而不是商加余数
易错举例
一副扑克有4种花色,每种花色13张,从中任意抽牌,最少要抽多少张才能保证有4张牌是同一花色?
解得对吗?
4×4=16(张)
答:最少要抽16张。
错误解答
易错举例
一副扑克有4种花色,每种花色13张,从中任意抽牌,最少要抽多少张才能保证有4张牌是同一花色?
解得对吗?
解得不对。
抽出12张扑克牌,每个抽屉都有3张,那么再任意摸出1张无论放到哪个抽屉都会出现一个抽屉里有4张牌。
温馨提示:用鸽巢问题解题时,常常要考虑最差情况
易错举例
一副扑克有4种花色,每种花色13张,从中任意抽牌,最少要抽多少张才能保证有4张牌是同一花色?
你能写出正确的答案吗?
3×4+1=13(张)
答:最少要抽13张。
5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?
5÷3=1……2
1+1=2
巩固拓展
11只鸽子飞进了4个鸽笼,总有一个鸽笼至少飞进了3只鸽子。为什么?
11÷4=2……3
2+1=3
巩固拓展
5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
5÷4=1······1
1+1=2
巩固拓展
向东小学六年级共有367名学生,其中六(2)班有49名学生。
他们说得对吗?为什么?
367÷365=1……2
1+1=2
49÷12=4……1
4+1=5
巩固拓展
把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到颜色相同的球?
我们从最不利的原则去考虑:
假设我们每种颜色的都拿一个,需要拿4个,但是没有同色的,要想有同色的需要再拿1个球,不论是哪一种颜色的,都一定有2个同色的。
4+1=5
巩固拓展
课堂小结
物体数÷抽屉数=商……余数
至少数:商+1
如果物体数除以抽屉数有余数,用所得的商加1,就会发现“总有一个抽屉里至少有商加1个物体”。
考虑问题要从最不利的原则去考虑。
课后作业
完成课后对应内容。
祝 你 学 习 进 步!
2022年春人教版数学
六年级下册数学精品课件
《第五单元 数学广角》
鸽巢问题
小学数学
情景导入
我给大家表演一个“魔术”。一副牌,取出大小王,还剩52张,你们5人每人随意抽一张,我知道至少有2张牌是同花色的。相信吗?
探究新知
探究新知
我把各种情况都摆出来了。
所以“至少”就是不能少于2支。
还可以这样想:先放3支,在每个笔筒中放1支,剩下的1支就要放进其中的一个笔筒。所以至少有一个笔筒中有2支铅笔。
探究新知
把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
如果每个抽屉最多放2本,那么3个抽屉最多放6本,可题目要求放的是7本书。所以……
两种放法都有一个抽屉放了3本或多于3本,所以……
我随便放放看,
一个抽屉1本,
一个抽屉2本,
一个抽屉4本。
探究新知
把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
如果有8本书会怎么样呢?10本呢?
7本书放进3个抽屉,有一个抽屉至少放3本书。8本书……
你是这样想的吗?你有什么发现?
7÷3=2……1
8÷3=2……2
10÷3=3……1
探究新知
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
探究新知
猜测1:只摸2个球就能保证是同色的。
第一种情况:
第二种情况:
第三种情况:
验证:球的颜色共有2种,如果只摸出2个球,会出现三种情况:1个红球和1个蓝球、2个红球、2个蓝球。因此,如果摸出的2个球正好是一红一蓝时就不能满足条件。
探究新知
猜测2:摸出5个球,肯定有2个是同色的。
第一种情况:
第二种情况:
第三种情况:
第四种情况:
验证:把红、蓝两种颜色看成2个“鸽巢”,因为5÷2=2……1,所以摸出5个球时,至少有3个球是同色的,显然,摸出5个球不是最少的。
猜测3:有两种颜色。那摸3个球就能保证有2个同色的球。
第一种情况:
第二种情况:
探究新知
生活中像这样的例子很多,我们能不能把这道题与前面所讲的“鸽巢问题”联系起来进行思考呢?
a.“摸球问题”与“鸽巢问题”有怎样的联系?
b.应该把什么看成“鸽巢”?有几个“鸽巢”?
要分放的东西是什么?
c.得出什么结论?
因为一共有红、蓝两种颜色的球,可以把两种“颜色”看成两个“鸽巢”,“同色”就意味着“同一个鸽巢”。这样,把“摸球问题”转化“鸽巢问题”,即“只要分的物体个数比鸽巢多,就能保证有一个鸽巢至少有两个球”。
探究新知
易错举例
因为11 ÷ 3 = 3……2,所以把11本书放进3个抽屉,总有一个抽屉至少放5本书。
这种说法是错误的。
至少放的书应该是“3(商)+1”,所以应该是4本。
温馨提示:解决此类题时要用商加1,而不是商加余数
×
这种说法是错误的。
至少放的书应该是“3(商)+1”,所以应该是4本。
温馨提示:解决此类题时要用商加1,而不是商加余数
易错举例
一副扑克有4种花色,每种花色13张,从中任意抽牌,最少要抽多少张才能保证有4张牌是同一花色?
解得对吗?
4×4=16(张)
答:最少要抽16张。
错误解答
易错举例
一副扑克有4种花色,每种花色13张,从中任意抽牌,最少要抽多少张才能保证有4张牌是同一花色?
解得对吗?
解得不对。
抽出12张扑克牌,每个抽屉都有3张,那么再任意摸出1张无论放到哪个抽屉都会出现一个抽屉里有4张牌。
温馨提示:用鸽巢问题解题时,常常要考虑最差情况
易错举例
一副扑克有4种花色,每种花色13张,从中任意抽牌,最少要抽多少张才能保证有4张牌是同一花色?
你能写出正确的答案吗?
3×4+1=13(张)
答:最少要抽13张。
5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?
5÷3=1……2
1+1=2
巩固拓展
11只鸽子飞进了4个鸽笼,总有一个鸽笼至少飞进了3只鸽子。为什么?
11÷4=2……3
2+1=3
巩固拓展
5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
5÷4=1······1
1+1=2
巩固拓展
向东小学六年级共有367名学生,其中六(2)班有49名学生。
他们说得对吗?为什么?
367÷365=1……2
1+1=2
49÷12=4……1
4+1=5
巩固拓展
把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到颜色相同的球?
我们从最不利的原则去考虑:
假设我们每种颜色的都拿一个,需要拿4个,但是没有同色的,要想有同色的需要再拿1个球,不论是哪一种颜色的,都一定有2个同色的。
4+1=5
巩固拓展
课堂小结
物体数÷抽屉数=商……余数
至少数:商+1
如果物体数除以抽屉数有余数,用所得的商加1,就会发现“总有一个抽屉里至少有商加1个物体”。
考虑问题要从最不利的原则去考虑。
课后作业
完成课后对应内容。
祝 你 学 习 进 步!
