苏科版八年级数学上第二章轴对称图形复习(第一课时)学案(无答案)
文档属性
| 名称 | 苏科版八年级数学上第二章轴对称图形复习(第一课时)学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 16:10:22 | ||
图片预览

文档简介
第二章 轴对称图形复习(第一课时)
【复习目标】
1、理清轴对称与轴对称图形有关概念,能熟练利用轴对称的性质设计简单轴对称图案.
2、掌握线段、角的相关性质定理及其逆定理,并能灵活应用上述知识解题.
【复习重点】轴对称与轴对称图形的有关概念;线段、角的相关性质定理及其逆定理.
【复习难点】灵活应用上述概念、定理准确解题.
【复习过程】
(一)自主梳理:
1、轴对称和轴对称图形
区别:轴对称是两个图形能沿对称轴折叠后能重合,指的是 个图形的位置关系.
而轴对称图形是指 个图形的两部分沿对称轴折叠后能完全重合,指的是具有对称性的 个图形.
联系:如果把成轴对称的两个图形看成一个整体,那么这个整体就是一个 .
如果把一个轴对称图形位于对称轴两旁的部分看成两个图形,那么这两部分图形就成 .
轴对称的性质:成轴对称的两个图形 ,对应点的连线被对称轴 .
2、线段的对称轴是它的 以及线段本身所在直线.
线段垂直平分线的性质定理: .
性质定理的逆定理: .
应用举例:三角形三边垂直平分线的交点到 距离相等.
3、角的对称轴是 .
角平分线的性质定理:__________________________________________________.
性质定理的逆定理:__________________________________________________________.
应用举例:三角形三个内角平分线的交点到 距离相等.
(二)基础自测:
1、判断:
⑴轴对称图形只有一条对称轴( )
⑵两个能重合的图形一定关于某条直线对称( )
⑶两个轴对称图形的对应点一定在对称轴的两侧( )
⑷轴对称图形指一个图形,而轴对称是指两个图形而言( )
2、填空:如图,△ABC中,DE是AC的垂直平分线,
⑴若AC=6,△ABD的周长是13,则△ABC的周长是 ;
⑵若△ABC的周长是30,△ABD的周长是25,则AC= ;
⑶若∠C=30°,则∠ADB= .
3、如图,∠C=900,AD平分∠CAB,若BC=10,BD=6,则D到边AB的距离为 .
4、选择:如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( ).A.50° B.40° C.30° D.20°
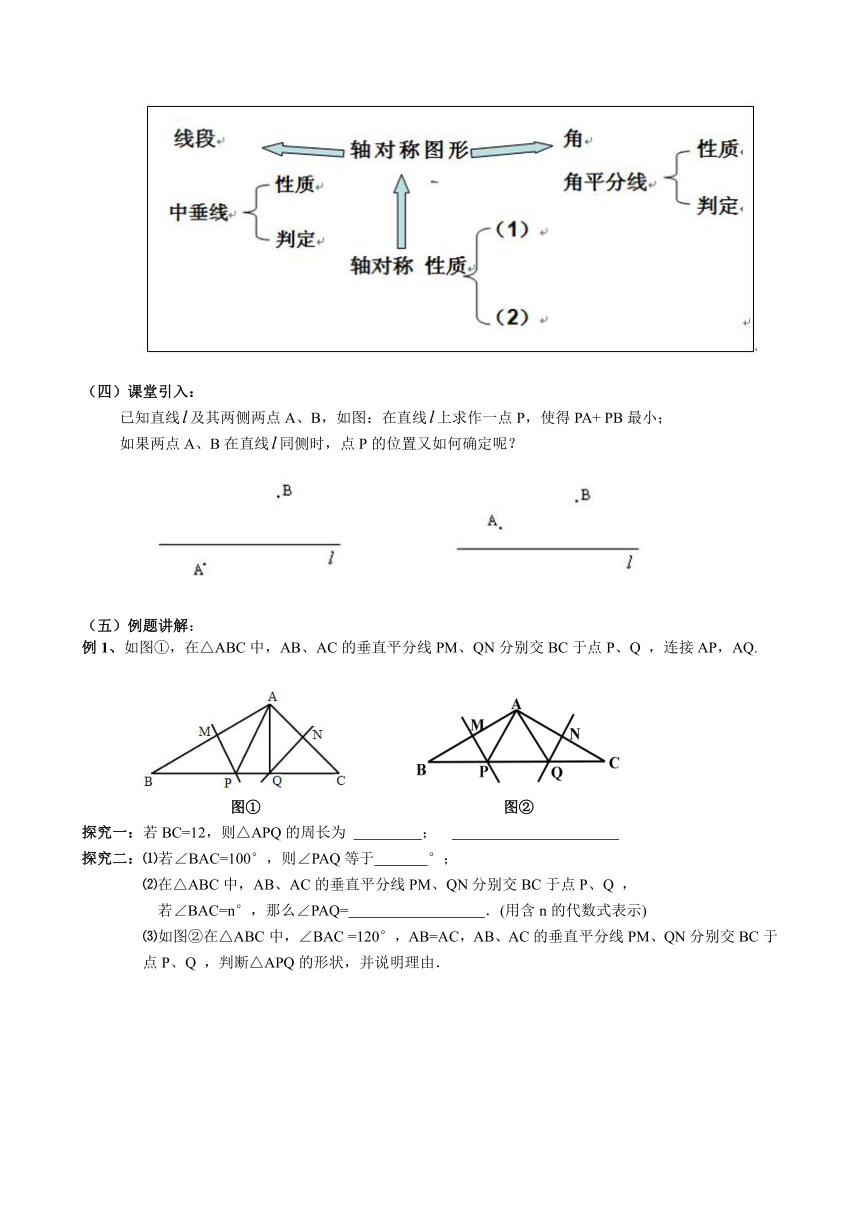
(三)知识成树:
(四)课堂引入:
已知直线及其两侧两点A、B,如图:在直线上求作一点P,使得PA+ PB最小;
如果两点A、B在直线同侧时,点P的位置又如何确定呢?
(五)例题讲解:
例1、如图①,在△ABC中,AB、AC的垂直平分线PM、QN分别交BC于点P、Q ,连接AP,AQ.
图① 图②
探究一:若BC=12,则△APQ的周长为 ;
探究二:⑴若∠BAC=100°,则∠PAQ等于 °;
⑵在△ABC中,AB、AC的垂直平分线PM、QN分别交BC于点P、Q ,
若∠BAC=n°,那么∠PAQ= .(用含n的代数式表示)
⑶如图②在△ABC中,∠BAC =120°,AB=AC,AB、AC的垂直平分线PM、QN分别交BC于点P、Q ,判断△APQ的形状,并说明理由.
例2、⑴画一画:如图①,OP是∠AOB的平分线,请你利用该图形画一对全等三角形,且以OP所在直线为对称轴,你用的判定全等方法是 .
⑵试一试:请你参考上题作全等三角形的方法,结合图②解答下列问题:在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
①求∠EFA= °;
②请你参考画一画作全等三角形的方法,结合图②:判断并写出FE与FD之间的数量关系,请说明理由.
(六)知识整合:(备用)
如图:△ABC中,∠C=90°,将△ABC折叠,使点B与点A重合,折痕分别交AB、BC于点E、F;∠ACB的平分线交直线EF于D;过点D作DG⊥CB于点G、作DH⊥CA交其延长线于点H.
⑴求证:AH=BG; ⑵若四边形ACBD的面积为25,则DH的长为 .
(七)课堂小结:这节课,你的收获是什么?你还有哪些疑惑?
(八)课后巩固:
1、下列四个艺术字中,不是轴对称的是【 】
2、下列四个图形中是轴对称图形且仅有一条对称轴的是【 】
A. B. C. D.
3、小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是【 】
A.21:10 B.10:21 C.10:51 D.12:01
4、如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有 种.
5、在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若AD=10,AC=8,则点D到AB的距离是 .
6、如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=700,则∠CBE= ,∠BEC= ;
(2)若BC=21cm,则△BCE的周长是 cm.
7、作出上图关于直线l的轴对称图形(不要求写出作法):
8、如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB
和直线MN,点A、B、M、N均在小正方形的顶点上.
(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),
使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点
为点D,点B的对称点为点C;
(2)四边形ABCD的周长= .
9、一次函数的图象与x、y轴分别交于点A(2,0),B(0,4).
(1)求该函数的解析式;
(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点坐标.
10、如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,点F、G分别在边AB、AC上,且DF=DG,△ADG的面积为15,△ADF的面积为10,求△DEF的面积.
(九)课堂反思:
第3题图
第4题图
第2题图
第3题图
第7题图
l
第6题图
第4题图
第8题图
第9题图
第10题图
【复习目标】
1、理清轴对称与轴对称图形有关概念,能熟练利用轴对称的性质设计简单轴对称图案.
2、掌握线段、角的相关性质定理及其逆定理,并能灵活应用上述知识解题.
【复习重点】轴对称与轴对称图形的有关概念;线段、角的相关性质定理及其逆定理.
【复习难点】灵活应用上述概念、定理准确解题.
【复习过程】
(一)自主梳理:
1、轴对称和轴对称图形
区别:轴对称是两个图形能沿对称轴折叠后能重合,指的是 个图形的位置关系.
而轴对称图形是指 个图形的两部分沿对称轴折叠后能完全重合,指的是具有对称性的 个图形.
联系:如果把成轴对称的两个图形看成一个整体,那么这个整体就是一个 .
如果把一个轴对称图形位于对称轴两旁的部分看成两个图形,那么这两部分图形就成 .
轴对称的性质:成轴对称的两个图形 ,对应点的连线被对称轴 .
2、线段的对称轴是它的 以及线段本身所在直线.
线段垂直平分线的性质定理: .
性质定理的逆定理: .
应用举例:三角形三边垂直平分线的交点到 距离相等.
3、角的对称轴是 .
角平分线的性质定理:__________________________________________________.
性质定理的逆定理:__________________________________________________________.
应用举例:三角形三个内角平分线的交点到 距离相等.
(二)基础自测:
1、判断:
⑴轴对称图形只有一条对称轴( )
⑵两个能重合的图形一定关于某条直线对称( )
⑶两个轴对称图形的对应点一定在对称轴的两侧( )
⑷轴对称图形指一个图形,而轴对称是指两个图形而言( )
2、填空:如图,△ABC中,DE是AC的垂直平分线,
⑴若AC=6,△ABD的周长是13,则△ABC的周长是 ;
⑵若△ABC的周长是30,△ABD的周长是25,则AC= ;
⑶若∠C=30°,则∠ADB= .
3、如图,∠C=900,AD平分∠CAB,若BC=10,BD=6,则D到边AB的距离为 .
4、选择:如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( ).A.50° B.40° C.30° D.20°
(三)知识成树:
(四)课堂引入:
已知直线及其两侧两点A、B,如图:在直线上求作一点P,使得PA+ PB最小;
如果两点A、B在直线同侧时,点P的位置又如何确定呢?
(五)例题讲解:
例1、如图①,在△ABC中,AB、AC的垂直平分线PM、QN分别交BC于点P、Q ,连接AP,AQ.
图① 图②
探究一:若BC=12,则△APQ的周长为 ;
探究二:⑴若∠BAC=100°,则∠PAQ等于 °;
⑵在△ABC中,AB、AC的垂直平分线PM、QN分别交BC于点P、Q ,
若∠BAC=n°,那么∠PAQ= .(用含n的代数式表示)
⑶如图②在△ABC中,∠BAC =120°,AB=AC,AB、AC的垂直平分线PM、QN分别交BC于点P、Q ,判断△APQ的形状,并说明理由.
例2、⑴画一画:如图①,OP是∠AOB的平分线,请你利用该图形画一对全等三角形,且以OP所在直线为对称轴,你用的判定全等方法是 .
⑵试一试:请你参考上题作全等三角形的方法,结合图②解答下列问题:在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
①求∠EFA= °;
②请你参考画一画作全等三角形的方法,结合图②:判断并写出FE与FD之间的数量关系,请说明理由.
(六)知识整合:(备用)
如图:△ABC中,∠C=90°,将△ABC折叠,使点B与点A重合,折痕分别交AB、BC于点E、F;∠ACB的平分线交直线EF于D;过点D作DG⊥CB于点G、作DH⊥CA交其延长线于点H.
⑴求证:AH=BG; ⑵若四边形ACBD的面积为25,则DH的长为 .
(七)课堂小结:这节课,你的收获是什么?你还有哪些疑惑?
(八)课后巩固:
1、下列四个艺术字中,不是轴对称的是【 】
2、下列四个图形中是轴对称图形且仅有一条对称轴的是【 】
A. B. C. D.
3、小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是【 】
A.21:10 B.10:21 C.10:51 D.12:01
4、如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有 种.
5、在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若AD=10,AC=8,则点D到AB的距离是 .
6、如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=700,则∠CBE= ,∠BEC= ;
(2)若BC=21cm,则△BCE的周长是 cm.
7、作出上图关于直线l的轴对称图形(不要求写出作法):
8、如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB
和直线MN,点A、B、M、N均在小正方形的顶点上.
(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),
使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点
为点D,点B的对称点为点C;
(2)四边形ABCD的周长= .
9、一次函数的图象与x、y轴分别交于点A(2,0),B(0,4).
(1)求该函数的解析式;
(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点坐标.
10、如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,点F、G分别在边AB、AC上,且DF=DG,△ADG的面积为15,△ADF的面积为10,求△DEF的面积.
(九)课堂反思:
第3题图
第4题图
第2题图
第3题图
第7题图
l
第6题图
第4题图
第8题图
第9题图
第10题图
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
