第四章 光单元检测(Word版含答案)
文档属性
| 名称 | 第四章 光单元检测(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 438.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-20 15:15:59 | ||
图片预览



文档简介
第四章 光 单元检测
一、单选题
1.对于波的折射现象,下列说法正确的是( )
A.当入射速度小于折射速度时,折射光线偏离法线
B.当波垂直界面入射时,传播方向不改变,波速和波长都不改变
C.在波的折射中,波的频率不改变,波速和波长都发生改变
D.波发生折射时一定不会发生反射现象
2.如图所示,已知介质Ⅰ为空气,介质Ⅱ的折射率为,则下列说法正确的是( )
A.光线、都不能发生全反射
B.光线、都能发生全反射
C.光线发生全反射,光线不发生全反射
D.光线不发生全反射,光线发生全反射
3.一单色光从空气中射到直角棱镜一个面上点,以入射角射入棱镜,经折射后射到另一面的点,恰好发生全反射,如图所示,则棱镜的折射率是( )
A. B. C. D.
4.如图所示,光线由空气射入半圆形玻璃砖,或由玻璃砖射入空气的光路图中,正确的是(玻璃的折射率为1.5)( )
A.图乙、丁 B.图甲、丁
C.图乙、丙 D.图甲、丙
5.在双缝干涉实验中,用波长为5×10-7m的黄光照射双缝。已知两缝间的间距为0.3mm,双缝到光屏的距离为1.2m,光屏上P点到双缝S1和S2的路程差为7.5×10-7m,则下列说法中正确的是( )
A.P点出现的是亮条纹,相邻两个亮条纹或暗条纹的中心间距为2mm
B.P点出现的是暗条纹,相邻两个亮条纹或暗条纹的中心间距为2mm
C.P点出现的是亮条纹,相邻两个亮条纹或暗条纹的中心间距为4mm
D.P点出现的是暗条纹,相邻两个亮条纹或暗条纹的中心间距为4mm
二、多选题
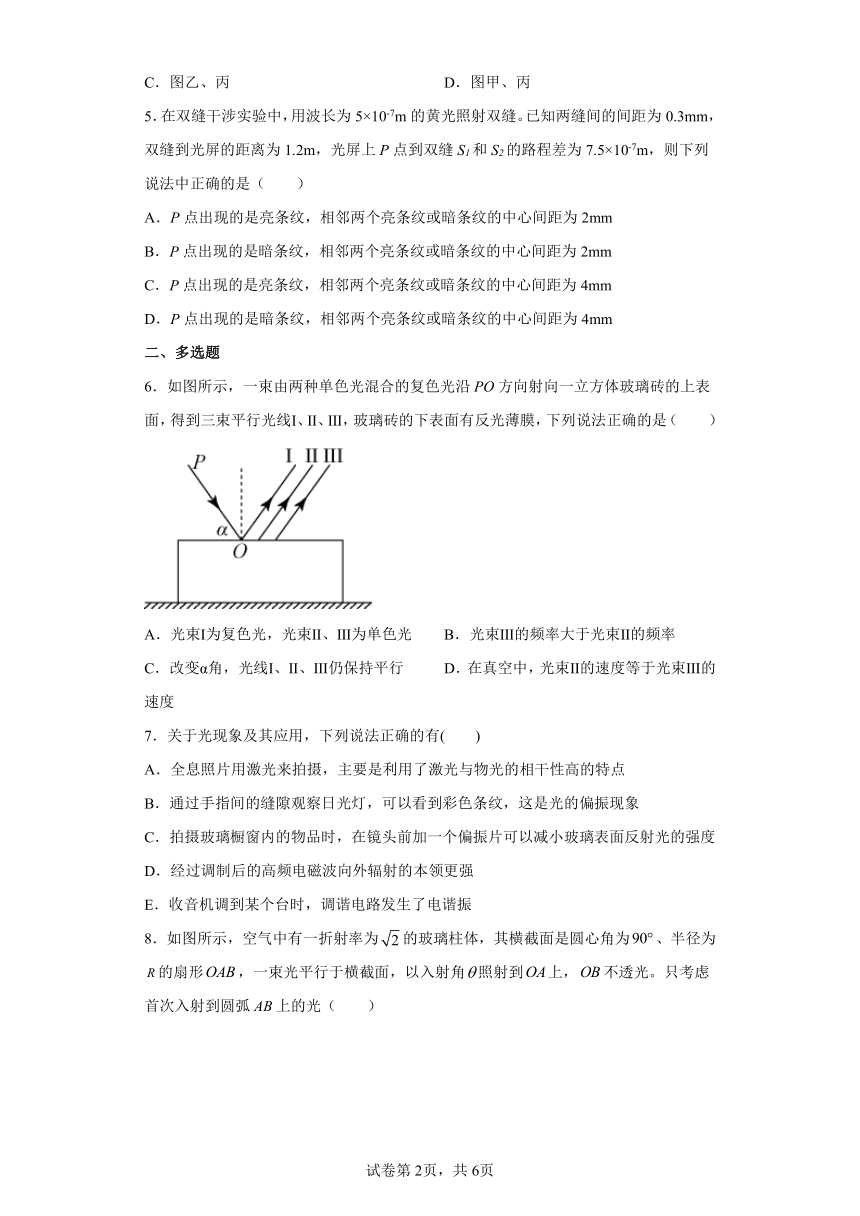
6.如图所示,一束由两种单色光混合的复色光沿PO方向射向一立方体玻璃砖的上表面,得到三束平行光线Ⅰ、Ⅱ、Ⅲ,玻璃砖的下表面有反光薄膜,下列说法正确的是( )
A.光束Ⅰ为复色光,光束Ⅱ、Ⅲ为单色光 B.光束Ⅲ的频率大于光束Ⅱ的频率
C.改变α角,光线Ⅰ、Ⅱ、Ⅲ仍保持平行 D.在真空中,光束Ⅱ的速度等于光束Ⅲ的速度
7.关于光现象及其应用,下列说法正确的有( )
A.全息照片用激光来拍摄,主要是利用了激光与物光的相干性高的特点
B.通过手指间的缝隙观察日光灯,可以看到彩色条纹,这是光的偏振现象
C.拍摄玻璃橱窗内的物品时,在镜头前加一个偏振片可以减小玻璃表面反射光的强度
D.经过调制后的高频电磁波向外辐射的本领更强
E.收音机调到某个台时,调谐电路发生了电谐振
8.如图所示,空气中有一折射率为的玻璃柱体,其横截面是圆心角为、半径为的扇形,一束光平行于横截面,以入射角照射到上,不透光。只考虑首次入射到圆弧上的光( )
A.若,则面上最大的入射角大于
B.若,则面上最大的入射角为
C.若,则上有光透出部分的弧长πR
D.若增大,则上有光透出部分的弧长变长
9.下列判断正确的是( )
A.水底同一深度并列红、黄、绿、紫四个小球,从水面正上方观察紫球最浅
B.爱因斯坦最早认识到了能量子的意义,提出光子说,并成功地解释了光电效应现象
C.均匀变化的电场产生均匀变化的磁场
D.在核反应堆的铀棒之间插入镉棒是为了控制核反应速度
10.如图所示,一束光从空气射向折射率为的某种玻璃的表面,i代表入射角,则__________.
A.只发生折射不发生反射,当入射角i=45°时,折射角r=30°
B.折射角随入射角增大而增大,但不会发生全反射
C.当入射角i增大时,折射角r不会超过45°
D.当i>45°时会发生全反射
E.当时,反射光线跟折射光线恰好垂直
11.关于光现象,下列说法正确的是( )
A.图a中一束白光通过三棱镜形成彩色光带是光的干涉现象
B.图b中光照射不透明的圆盘,在圆盘的阴影中心出现了一个亮斑是光的衍射现象
C.图c中肥皂膜上出现彩色条纹是光的干射现象
D.图d中佩戴特殊眼镜观看立体电影利用了光的偏振现象
三、实验题
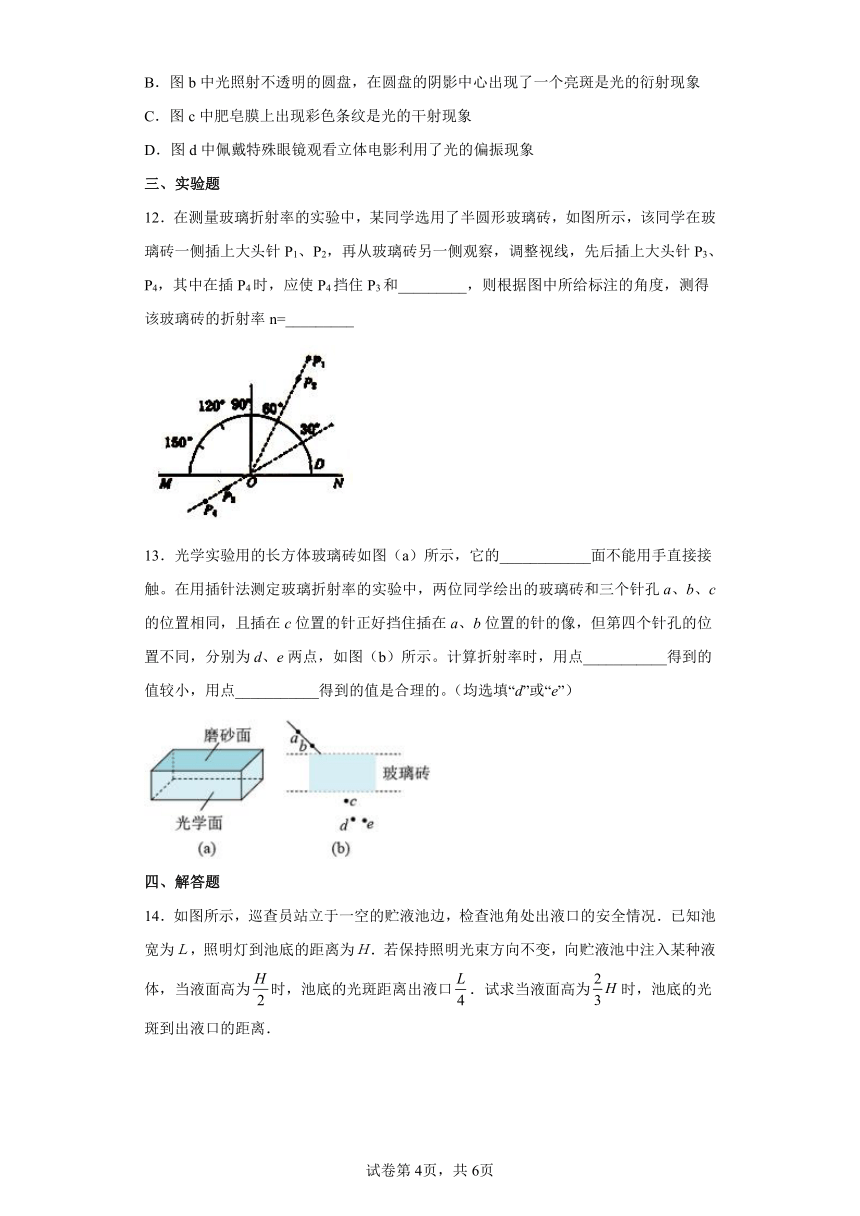
12.在测量玻璃折射率的实验中,某同学选用了半圆形玻璃砖,如图所示,该同学在玻璃砖一侧插上大头针P1、P2,再从玻璃砖另一侧观察,调整视线,先后插上大头针P3、P4,其中在插P4时,应使P4挡住P3和_________,则根据图中所给标注的角度,测得该玻璃砖的折射率n=_________
13.光学实验用的长方体玻璃砖如图(a)所示,它的____________面不能用手直接接触。在用插针法测定玻璃折射率的实验中,两位同学绘出的玻璃砖和三个针孔a、b、c的位置相同,且插在c位置的针正好挡住插在a、b位置的针的像,但第四个针孔的位置不同,分别为d、e两点,如图(b)所示。计算折射率时,用点___________得到的值较小,用点___________得到的值是合理的。(均选填“d”或“e”)
四、解答题
14.如图所示,巡查员站立于一空的贮液池边,检查池角处出液口的安全情况.已知池宽为L,照明灯到池底的距离为H.若保持照明光束方向不变,向贮液池中注入某种液体,当液面高为时,池底的光斑距离出液口.试求当液面高为时,池底的光斑到出液口的距离.
15.有一玻璃半球,右侧面镀银,光源S在其对称轴PO上(O为半球的球心),且PO水平,如图所示,从光源S发出的一细光束射到半球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光经过折射进入玻璃半球内,经右侧镀银面反射恰能沿原路返回,若球面半径为R,玻璃折射率为,求:
①光源S与球心O之间的距离;
②折射进入玻璃半球内的光线在球内经过的时间.
16.如图,一圆筒形均匀透明介质,AB为外圆的直径,外圆半径是内圆半径的2倍,内圆半径为R。在介质横截面内,从A点光源处向介质内发射一与内圆相切的光线,光线到达外圆边界时发生反射和折射,其折射光线与反射光线垂直,最终有光线又返回A点,已知光在真空中的速度为c,求:
①介质材料的折射率;
②第一次返回A点的光线在介质中传播的时间。
17.如图所示,太阳光平行射入一半径为R的水球,以波长为的红光为例,它经折射、反射、折射后射出,入射角为,红光在水中的折射率为n,在真空中的折射率为1,真空中的光速为c。求:
(1)红光在水球中传播的距离;
(2)红光在水球中传播的时间。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
【详解】
A.当入射速度小于折射速度时,折射光线不一定偏离法线,当入射角为零度时,折射光线与法线重合,故A错误;
B.当波垂直界面入射时,传播方向不改变,但波速和波长都发生改变,故B错误;
C.波的频率由波源决定,与介质无关,在波的折射中,波的频率不改变,波速和波长都改变,故C正确;
D.波发生折射时在同一个界面也可发生反射现象,故D错误。
故选C。
2.A
【解析】
【分析】
【详解】
光从光密介质射向光疏介质时可能发生全反射,介质Ⅱ对介质Ⅰ来说是光密介质,光线不能发生全反射,光线可能发生全反射,又全反射临界角满足
则
题图中光线与界面的夹角为,则此时的入射角为,故光线不能发生全反射。
故选A。
3.A
【解析】
【详解】
作出光路图如图所示:
光线在点发生了折射,则有:
据题意知光线在点恰好发生了全反射,入射角等于临界角.
由几何知识有:
所以可得:
即得:
又:
则:
联立可得:
解得:
故A正确,BCD错误.
故选A.
【点睛】
解决光学问题的关键要掌握全反射的条件、折射定律、临界角公式、光速公式,运用几何知识结合解决这类问题.
4.A
【解析】
【详解】
甲、乙、光线从空气射入半圆形玻璃砖时折射角应小于入射角,故甲错误,乙正确;丙、丁、光线由玻璃砖射入空气时,设临界角为C,则有
则
由图知:入射角
所以光线发生了全反射,故丙错误,丁正确,综上可知A正确,BCD错误。
5.B
【解析】
【详解】
光屏上P点到双缝S1和S2的路程差为7.5×10-7m,黄光的波长为5×10-7m ,则
为奇数,在P点出现暗条纹,相邻两个亮条纹或暗条纹的中心间距为
B正确,ACD错误。
故选B。
6.ACD
【解析】
【分析】
【详解】
A.两种色光都在玻璃砖的上表面发生了反射,入射角相同,由反射定律知,它们的反射角相同,可知光束Ⅰ是复色光,而光束Ⅱ、Ⅲ由于折射率的不同导致偏折分离,所以光束Ⅱ、Ⅲ为单色光,故A正确;
B.由图可知
光束Ⅱ的偏折程度大于光束Ⅲ的偏折程度,根据折射定律可知玻璃对光束Ⅱ的折射率大于对光束Ⅲ的折射率,则光束Ⅱ的频率大于光束Ⅲ的频率,故B错误;
C.一束由两种单色光混合的复色光沿PO方向射入,经过折射、反射、再折射后,光线仍平行,这是因为光反射时入射角与反射角相等,改变α角,光线Ⅰ、Ⅱ、Ⅲ仍保持平行,故C正确;
D.在真空中,所有光的速度都相等,故D正确。
故选ACD。
7.ACDE
【解析】
【详解】
A.全息照片用激光来拍摄,主要是利用了激光与物光的相干性高的特点,选项A正确;
B.通过手指间的缝隙观察日光灯,可以看到彩色条纹,这是光的衍射现象,选项B错误;
C.拍摄玻璃橱窗内的物品时,在镜头前加一个偏振片可以减小玻璃表面反射光的强度,从而使得拍摄照片更清晰,选项C正确;
D.调制是把低频信号加到高频电磁波上增强发射能力,频率变大,穿透能力更强,即辐射本领更强,选项D正确;
E.收音机调到某个台时,调谐电路发生了电谐振,选项E正确。
故选ACDE。
8.AC
【解析】
【详解】
根据折射定律有,可得光进入玻璃后光线与竖直方向的夹角为,过的光线垂直入射到界面上点射出,到之间没有光线射出;越接近的光线入射到界面上时的入射角越大,根据临界角公式得临界角为,即面上最大的入射角大于;如果界面上的临界点为,此光线在界面上点入射,在三角形中可求得与水平方向的夹角为,所以到之间没有光线射出,由此可得有光线射出的圆弧对应圆心角为,有光透出部分的弧长为;增大,则折射角也增大,根据几何关系,设折射角为,则有光线射出的部分对应的圆心角为,知对应的弧长不变,故选项A、C正确,B、D错误。
9.ABD
【解析】
【详解】
A.光折射成像时,视深
水底同一深度并列红、黄、绿、紫四个色球,紫光的折射率最大,故紫球视深最浅,故A正确;
B.爱因斯坦最早认识到了能量子的意义,提出光子说,并成功地解释了光电效应现象,选项B正确;
C.根据麦克斯韦电磁理论,均匀变化的电场产生稳定的磁场,选项C错误;
D.在核反应堆的铀棒之间插入镉棒是为了控制核反应速度,选项D正确。
故选ABD。
10.BCE
【解析】
【详解】
A.光从空气射向玻璃不仅发生折射还发生反射,故A错误;
B.折射角随入射角增大而增大,要发生全发射光必须从光密介质进入光疏介质,故B正确;
C.当时,,故C正确;
D.要发生全发射光必须从光密介质进入光疏介质,故D错误;
E.当反射光线跟折射光线恰好垂直时,反射角与折射角之和等于,由因反射角等于入射角,所以,由
故E正确,
故选BCE.
11.BCD
【解析】
【详解】
A.图a中一束白光通过三棱镜形成彩色光带是光的折射,故A错误;
B.图b中光照射不透明的圆盘,在圆盘的阴影中心出现了一个亮斑是泊松亮斑,是光的衍射现象,故B正确;
C.图c中肥皂膜上出现彩色条纹是光在前后膜的反射光叠加产生的,是光的干涉现象,故C正确;
D.图d中立体电影在放映时,是两台放映机发出相互垂直的偏振光,佩戴特殊眼镜观看立体电影,才能获得最佳观赏效果,利用了光的偏振原理,故D正确。
故选BCD。
12. P1、P2的像
【解析】
【详解】
连接P1、P2表示入射光线,连接P3、P4表示出射光线,连接两光线与玻璃砖的交点,即为折射光线,作出光路图如图,根据折射定律,得知玻璃折射率,所以 先后插上大头针P3、P4,其中在插P4时,应使P4挡住P3和P1、P2的像,测得该玻璃砖的折射率.
13. 光学面 d e
【解析】
【分析】
【详解】
[1]玻璃砖的光学面不能用手直接接触,接触面的污渍会影响接触面的平整,进而影响折射率的测定;
[2][3]连接dc、ec并延长至玻璃砖的光学面与白纸的交线,交点为出射点,入射点与出射点的连线即为折射光线,入射角一定,用d点时,折射角大,折射率小;对于两光学面平行的玻璃砖,入射光线和出射光线平行,ec连线与入射光线平行,误差小即更合理,如图所示
14.
【解析】
【分析】
当光从空气射向水中时,根据几何关系从而确定入射角的正弦值与折射角的正弦值,从而由光的折射定律可算出水的折射率.当液面高度改变时,即入射点发生变化,但入射角与折射角均没有变化,所以通过几何关系可以确定池底的光斑到出液口的距离.
【详解】
设液面的高度为h,光斑到到入射点的水平距离为l,则:
由几何关系得: ;sinθ1= ;sinθ2=
由折射定律得:
将h=0.5H,l=0.25L代入得
当h=H,有:l′=L-x′
联立以上各式得:
【点睛】
点睛:此题考查光的折射定律的应用;问题中虽然液面高度变化,但由于入射角没变,则折射角也不变.于是可以根据几何关系来构建长度关系,从而求出所求结果.
15.①. ②
【解析】
【详解】
①由题意可知折射光线与镜面垂直,其光路图如图所示,则有:
i+r=90°
由折射定律可得:
解得:i=60° r=30°
在直角三角形ABO中:BO =Rcosr=
由几何关系可得:
△SAO为等腰三角形,所以SO=2BO=
②光在玻璃半球内传播的速度
光在玻璃半球内传播的距离
则光折射进入玻璃半球内的光线在球内经过的时间
16.①;②
【解析】
【详解】
①光路如图:
由几何关系可知ODAC,则有
解得
由折射光线与反射光线垂直,则
由折射定律
② 根据几何关系可得
光线在介质中的速度
解得
17.(1);(2)
【解析】
【详解】
(1)根据折射定律有
①
由几何关系可知红光在水球中传播的距离为
②
(2)红光在水球中的传播速度为
③
则传播时间为
④
答案第1页,共2页
答案第1页,共2页
一、单选题
1.对于波的折射现象,下列说法正确的是( )
A.当入射速度小于折射速度时,折射光线偏离法线
B.当波垂直界面入射时,传播方向不改变,波速和波长都不改变
C.在波的折射中,波的频率不改变,波速和波长都发生改变
D.波发生折射时一定不会发生反射现象
2.如图所示,已知介质Ⅰ为空气,介质Ⅱ的折射率为,则下列说法正确的是( )
A.光线、都不能发生全反射
B.光线、都能发生全反射
C.光线发生全反射,光线不发生全反射
D.光线不发生全反射,光线发生全反射
3.一单色光从空气中射到直角棱镜一个面上点,以入射角射入棱镜,经折射后射到另一面的点,恰好发生全反射,如图所示,则棱镜的折射率是( )
A. B. C. D.
4.如图所示,光线由空气射入半圆形玻璃砖,或由玻璃砖射入空气的光路图中,正确的是(玻璃的折射率为1.5)( )
A.图乙、丁 B.图甲、丁
C.图乙、丙 D.图甲、丙
5.在双缝干涉实验中,用波长为5×10-7m的黄光照射双缝。已知两缝间的间距为0.3mm,双缝到光屏的距离为1.2m,光屏上P点到双缝S1和S2的路程差为7.5×10-7m,则下列说法中正确的是( )
A.P点出现的是亮条纹,相邻两个亮条纹或暗条纹的中心间距为2mm
B.P点出现的是暗条纹,相邻两个亮条纹或暗条纹的中心间距为2mm
C.P点出现的是亮条纹,相邻两个亮条纹或暗条纹的中心间距为4mm
D.P点出现的是暗条纹,相邻两个亮条纹或暗条纹的中心间距为4mm
二、多选题
6.如图所示,一束由两种单色光混合的复色光沿PO方向射向一立方体玻璃砖的上表面,得到三束平行光线Ⅰ、Ⅱ、Ⅲ,玻璃砖的下表面有反光薄膜,下列说法正确的是( )
A.光束Ⅰ为复色光,光束Ⅱ、Ⅲ为单色光 B.光束Ⅲ的频率大于光束Ⅱ的频率
C.改变α角,光线Ⅰ、Ⅱ、Ⅲ仍保持平行 D.在真空中,光束Ⅱ的速度等于光束Ⅲ的速度
7.关于光现象及其应用,下列说法正确的有( )
A.全息照片用激光来拍摄,主要是利用了激光与物光的相干性高的特点
B.通过手指间的缝隙观察日光灯,可以看到彩色条纹,这是光的偏振现象
C.拍摄玻璃橱窗内的物品时,在镜头前加一个偏振片可以减小玻璃表面反射光的强度
D.经过调制后的高频电磁波向外辐射的本领更强
E.收音机调到某个台时,调谐电路发生了电谐振
8.如图所示,空气中有一折射率为的玻璃柱体,其横截面是圆心角为、半径为的扇形,一束光平行于横截面,以入射角照射到上,不透光。只考虑首次入射到圆弧上的光( )
A.若,则面上最大的入射角大于
B.若,则面上最大的入射角为
C.若,则上有光透出部分的弧长πR
D.若增大,则上有光透出部分的弧长变长
9.下列判断正确的是( )
A.水底同一深度并列红、黄、绿、紫四个小球,从水面正上方观察紫球最浅
B.爱因斯坦最早认识到了能量子的意义,提出光子说,并成功地解释了光电效应现象
C.均匀变化的电场产生均匀变化的磁场
D.在核反应堆的铀棒之间插入镉棒是为了控制核反应速度
10.如图所示,一束光从空气射向折射率为的某种玻璃的表面,i代表入射角,则__________.
A.只发生折射不发生反射,当入射角i=45°时,折射角r=30°
B.折射角随入射角增大而增大,但不会发生全反射
C.当入射角i增大时,折射角r不会超过45°
D.当i>45°时会发生全反射
E.当时,反射光线跟折射光线恰好垂直
11.关于光现象,下列说法正确的是( )
A.图a中一束白光通过三棱镜形成彩色光带是光的干涉现象
B.图b中光照射不透明的圆盘,在圆盘的阴影中心出现了一个亮斑是光的衍射现象
C.图c中肥皂膜上出现彩色条纹是光的干射现象
D.图d中佩戴特殊眼镜观看立体电影利用了光的偏振现象
三、实验题
12.在测量玻璃折射率的实验中,某同学选用了半圆形玻璃砖,如图所示,该同学在玻璃砖一侧插上大头针P1、P2,再从玻璃砖另一侧观察,调整视线,先后插上大头针P3、P4,其中在插P4时,应使P4挡住P3和_________,则根据图中所给标注的角度,测得该玻璃砖的折射率n=_________
13.光学实验用的长方体玻璃砖如图(a)所示,它的____________面不能用手直接接触。在用插针法测定玻璃折射率的实验中,两位同学绘出的玻璃砖和三个针孔a、b、c的位置相同,且插在c位置的针正好挡住插在a、b位置的针的像,但第四个针孔的位置不同,分别为d、e两点,如图(b)所示。计算折射率时,用点___________得到的值较小,用点___________得到的值是合理的。(均选填“d”或“e”)
四、解答题
14.如图所示,巡查员站立于一空的贮液池边,检查池角处出液口的安全情况.已知池宽为L,照明灯到池底的距离为H.若保持照明光束方向不变,向贮液池中注入某种液体,当液面高为时,池底的光斑距离出液口.试求当液面高为时,池底的光斑到出液口的距离.
15.有一玻璃半球,右侧面镀银,光源S在其对称轴PO上(O为半球的球心),且PO水平,如图所示,从光源S发出的一细光束射到半球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光经过折射进入玻璃半球内,经右侧镀银面反射恰能沿原路返回,若球面半径为R,玻璃折射率为,求:
①光源S与球心O之间的距离;
②折射进入玻璃半球内的光线在球内经过的时间.
16.如图,一圆筒形均匀透明介质,AB为外圆的直径,外圆半径是内圆半径的2倍,内圆半径为R。在介质横截面内,从A点光源处向介质内发射一与内圆相切的光线,光线到达外圆边界时发生反射和折射,其折射光线与反射光线垂直,最终有光线又返回A点,已知光在真空中的速度为c,求:
①介质材料的折射率;
②第一次返回A点的光线在介质中传播的时间。
17.如图所示,太阳光平行射入一半径为R的水球,以波长为的红光为例,它经折射、反射、折射后射出,入射角为,红光在水中的折射率为n,在真空中的折射率为1,真空中的光速为c。求:
(1)红光在水球中传播的距离;
(2)红光在水球中传播的时间。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
【详解】
A.当入射速度小于折射速度时,折射光线不一定偏离法线,当入射角为零度时,折射光线与法线重合,故A错误;
B.当波垂直界面入射时,传播方向不改变,但波速和波长都发生改变,故B错误;
C.波的频率由波源决定,与介质无关,在波的折射中,波的频率不改变,波速和波长都改变,故C正确;
D.波发生折射时在同一个界面也可发生反射现象,故D错误。
故选C。
2.A
【解析】
【分析】
【详解】
光从光密介质射向光疏介质时可能发生全反射,介质Ⅱ对介质Ⅰ来说是光密介质,光线不能发生全反射,光线可能发生全反射,又全反射临界角满足
则
题图中光线与界面的夹角为,则此时的入射角为,故光线不能发生全反射。
故选A。
3.A
【解析】
【详解】
作出光路图如图所示:
光线在点发生了折射,则有:
据题意知光线在点恰好发生了全反射,入射角等于临界角.
由几何知识有:
所以可得:
即得:
又:
则:
联立可得:
解得:
故A正确,BCD错误.
故选A.
【点睛】
解决光学问题的关键要掌握全反射的条件、折射定律、临界角公式、光速公式,运用几何知识结合解决这类问题.
4.A
【解析】
【详解】
甲、乙、光线从空气射入半圆形玻璃砖时折射角应小于入射角,故甲错误,乙正确;丙、丁、光线由玻璃砖射入空气时,设临界角为C,则有
则
由图知:入射角
所以光线发生了全反射,故丙错误,丁正确,综上可知A正确,BCD错误。
5.B
【解析】
【详解】
光屏上P点到双缝S1和S2的路程差为7.5×10-7m,黄光的波长为5×10-7m ,则
为奇数,在P点出现暗条纹,相邻两个亮条纹或暗条纹的中心间距为
B正确,ACD错误。
故选B。
6.ACD
【解析】
【分析】
【详解】
A.两种色光都在玻璃砖的上表面发生了反射,入射角相同,由反射定律知,它们的反射角相同,可知光束Ⅰ是复色光,而光束Ⅱ、Ⅲ由于折射率的不同导致偏折分离,所以光束Ⅱ、Ⅲ为单色光,故A正确;
B.由图可知
光束Ⅱ的偏折程度大于光束Ⅲ的偏折程度,根据折射定律可知玻璃对光束Ⅱ的折射率大于对光束Ⅲ的折射率,则光束Ⅱ的频率大于光束Ⅲ的频率,故B错误;
C.一束由两种单色光混合的复色光沿PO方向射入,经过折射、反射、再折射后,光线仍平行,这是因为光反射时入射角与反射角相等,改变α角,光线Ⅰ、Ⅱ、Ⅲ仍保持平行,故C正确;
D.在真空中,所有光的速度都相等,故D正确。
故选ACD。
7.ACDE
【解析】
【详解】
A.全息照片用激光来拍摄,主要是利用了激光与物光的相干性高的特点,选项A正确;
B.通过手指间的缝隙观察日光灯,可以看到彩色条纹,这是光的衍射现象,选项B错误;
C.拍摄玻璃橱窗内的物品时,在镜头前加一个偏振片可以减小玻璃表面反射光的强度,从而使得拍摄照片更清晰,选项C正确;
D.调制是把低频信号加到高频电磁波上增强发射能力,频率变大,穿透能力更强,即辐射本领更强,选项D正确;
E.收音机调到某个台时,调谐电路发生了电谐振,选项E正确。
故选ACDE。
8.AC
【解析】
【详解】
根据折射定律有,可得光进入玻璃后光线与竖直方向的夹角为,过的光线垂直入射到界面上点射出,到之间没有光线射出;越接近的光线入射到界面上时的入射角越大,根据临界角公式得临界角为,即面上最大的入射角大于;如果界面上的临界点为,此光线在界面上点入射,在三角形中可求得与水平方向的夹角为,所以到之间没有光线射出,由此可得有光线射出的圆弧对应圆心角为,有光透出部分的弧长为;增大,则折射角也增大,根据几何关系,设折射角为,则有光线射出的部分对应的圆心角为,知对应的弧长不变,故选项A、C正确,B、D错误。
9.ABD
【解析】
【详解】
A.光折射成像时,视深
水底同一深度并列红、黄、绿、紫四个色球,紫光的折射率最大,故紫球视深最浅,故A正确;
B.爱因斯坦最早认识到了能量子的意义,提出光子说,并成功地解释了光电效应现象,选项B正确;
C.根据麦克斯韦电磁理论,均匀变化的电场产生稳定的磁场,选项C错误;
D.在核反应堆的铀棒之间插入镉棒是为了控制核反应速度,选项D正确。
故选ABD。
10.BCE
【解析】
【详解】
A.光从空气射向玻璃不仅发生折射还发生反射,故A错误;
B.折射角随入射角增大而增大,要发生全发射光必须从光密介质进入光疏介质,故B正确;
C.当时,,故C正确;
D.要发生全发射光必须从光密介质进入光疏介质,故D错误;
E.当反射光线跟折射光线恰好垂直时,反射角与折射角之和等于,由因反射角等于入射角,所以,由
故E正确,
故选BCE.
11.BCD
【解析】
【详解】
A.图a中一束白光通过三棱镜形成彩色光带是光的折射,故A错误;
B.图b中光照射不透明的圆盘,在圆盘的阴影中心出现了一个亮斑是泊松亮斑,是光的衍射现象,故B正确;
C.图c中肥皂膜上出现彩色条纹是光在前后膜的反射光叠加产生的,是光的干涉现象,故C正确;
D.图d中立体电影在放映时,是两台放映机发出相互垂直的偏振光,佩戴特殊眼镜观看立体电影,才能获得最佳观赏效果,利用了光的偏振原理,故D正确。
故选BCD。
12. P1、P2的像
【解析】
【详解】
连接P1、P2表示入射光线,连接P3、P4表示出射光线,连接两光线与玻璃砖的交点,即为折射光线,作出光路图如图,根据折射定律,得知玻璃折射率,所以 先后插上大头针P3、P4,其中在插P4时,应使P4挡住P3和P1、P2的像,测得该玻璃砖的折射率.
13. 光学面 d e
【解析】
【分析】
【详解】
[1]玻璃砖的光学面不能用手直接接触,接触面的污渍会影响接触面的平整,进而影响折射率的测定;
[2][3]连接dc、ec并延长至玻璃砖的光学面与白纸的交线,交点为出射点,入射点与出射点的连线即为折射光线,入射角一定,用d点时,折射角大,折射率小;对于两光学面平行的玻璃砖,入射光线和出射光线平行,ec连线与入射光线平行,误差小即更合理,如图所示
14.
【解析】
【分析】
当光从空气射向水中时,根据几何关系从而确定入射角的正弦值与折射角的正弦值,从而由光的折射定律可算出水的折射率.当液面高度改变时,即入射点发生变化,但入射角与折射角均没有变化,所以通过几何关系可以确定池底的光斑到出液口的距离.
【详解】
设液面的高度为h,光斑到到入射点的水平距离为l,则:
由几何关系得: ;sinθ1= ;sinθ2=
由折射定律得:
将h=0.5H,l=0.25L代入得
当h=H,有:l′=L-x′
联立以上各式得:
【点睛】
点睛:此题考查光的折射定律的应用;问题中虽然液面高度变化,但由于入射角没变,则折射角也不变.于是可以根据几何关系来构建长度关系,从而求出所求结果.
15.①. ②
【解析】
【详解】
①由题意可知折射光线与镜面垂直,其光路图如图所示,则有:
i+r=90°
由折射定律可得:
解得:i=60° r=30°
在直角三角形ABO中:BO =Rcosr=
由几何关系可得:
△SAO为等腰三角形,所以SO=2BO=
②光在玻璃半球内传播的速度
光在玻璃半球内传播的距离
则光折射进入玻璃半球内的光线在球内经过的时间
16.①;②
【解析】
【详解】
①光路如图:
由几何关系可知ODAC,则有
解得
由折射光线与反射光线垂直,则
由折射定律
② 根据几何关系可得
光线在介质中的速度
解得
17.(1);(2)
【解析】
【详解】
(1)根据折射定律有
①
由几何关系可知红光在水球中传播的距离为
②
(2)红光在水球中的传播速度为
③
则传播时间为
④
答案第1页,共2页
答案第1页,共2页
