西师大版五年级下册数学《5.4.2 解方程(二)》表格式教案
文档属性
| 名称 | 西师大版五年级下册数学《5.4.2 解方程(二)》表格式教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 24.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 00:00:00 | ||
图片预览

文档简介
5.4.2 解方程(二)
学习内容 教科书第84页例3及课堂活动第1、2题,练习二十四第4~6题。
育人目标 1.结合具体情景,认识形如a±b=c这类方程,理解其现实意义。 2.探究并理解解形如a±b=c这类方程的基本思路,能用等式的性质解这类方程。 3.会检验形如a±b=c这类方程解方程的结果。
学习重难点 重点:能用等式的性质解形如a±b=c这类方程。 难点:探究并理解解形如a±b=c这类方程的基本思路。
教学过程
环节 教师活动 学生活动 五育融合育人点提示
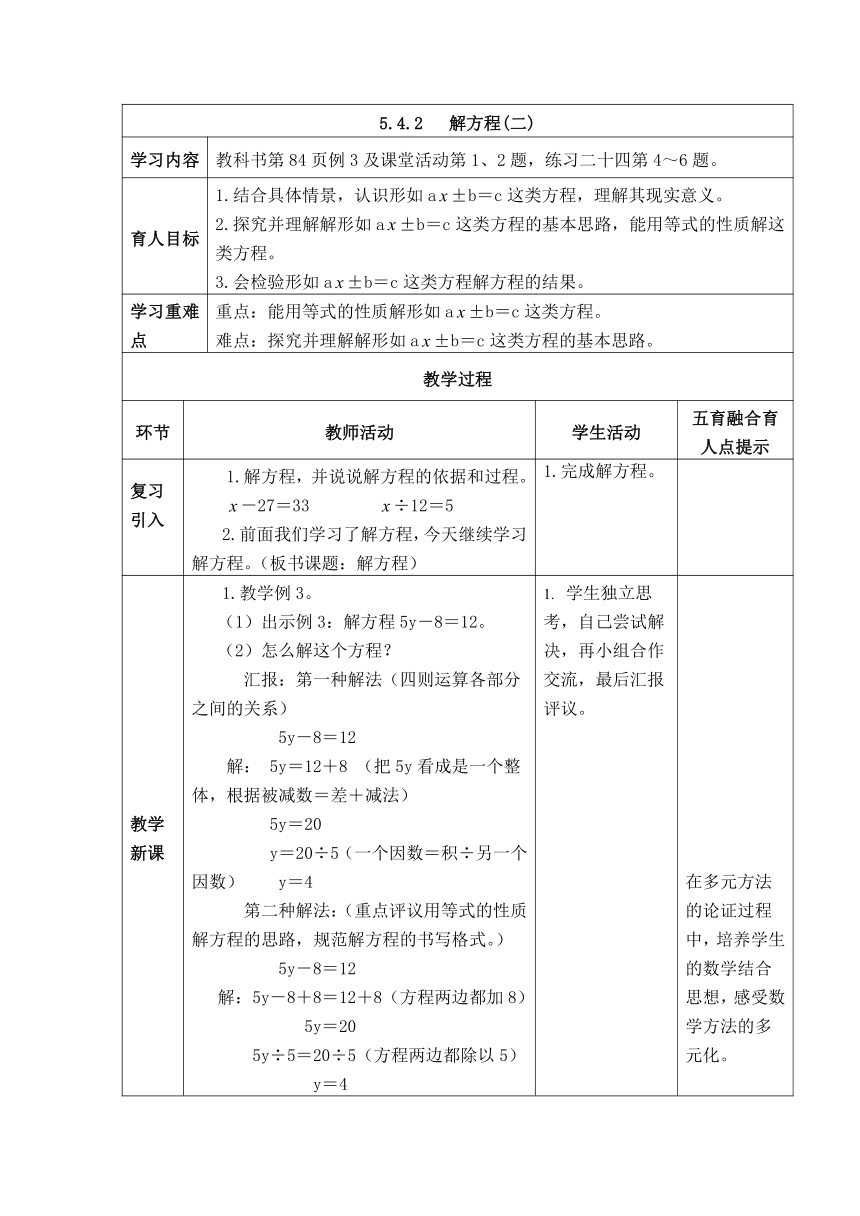
复习引入 1.解方程,并说说解方程的依据和过程。 -27=33 ÷12=5 2.前面我们学习了解方程,今天继续学习解方程。(板书课题:解方程) 1.完成解方程。
教学新课 1.教学例3。 (1)出示例3:解方程5y-8=12。 (2)怎么解这个方程? 汇报:第一种解法(四则运算各部分之间的关系) 5y-8=12 解: 5y=12+8 (把5y看成是一个整体,根据被减数=差+减法) 5y=20 y=20÷5(一个因数=积÷另一个因数) y=4 第二种解法:(重点评议用等式的性质解方程的思路,规范解方程的书写格式。) 5y-8=12 解:5y-8+8=12+8(方程两边都加8) 5y=20 5y÷5=20÷5(方程两边都除以5) y=4 第一步,为什么要方程的两边都加8? 第二步,为什么要方程的两边都除以5? ④归纳小结。 对比:两种解法有什么不同? 强调:解像5y-8=12这种方程,既可以根据加、减、乘、除各部分之间的关系来解,也可以用等式的性质来解,但是为了以后能解更复杂的方程,我们提倡用等式的性质来解。 (3)解得对不对?怎么验算呢? 检验:把y=4代入原方程, 左边=5×4-8 =20-8 =12=右边 所以y=4是原方程的解。 (4)回顾总结:今天学习的解方程与前面学习的解方程有什么不同点和相同点? 不同点:计算步骤不同。 相同点:都是用等式的性质来解方程;书写格式相同;检验的方法相同。 (5)完成例3下面的“试一试”。 解方程:18+6=30 4n-2.5×4=15 部分学生解第二个方程可能有困难,可以让学生先思考,这个方程与前面学习的方程有什么不同?应该先这么办?让学生明确先算出2.5×4的积,就变成了学过的方程的类型。 学生独立思考,自己尝试解决,再小组合作交流,最后汇报评议。 2.理解两种解法的依据。 3.验算。 4.回顾总结并完成“试一试”,再集体评议。 在多元方法的论证过程中,培养学生的数学结合思想,感受数学方法的多元化。 在验证的过程中,培养学生的严谨意识。
应用练习 1.完成第84页课堂活动第1、2题。 2.练习二十四第4、5题。 (1)学生先独立列方程,评议。 (2)学生独立解方程,评议。 3.独立完成练习二十四第6题。 学生独立完成,再集体评议。 及时练习,培养学生知识的应用能力。
反思总结 今天学习了什么?谈谈你的收获。 1.今天学习的解方程与前面学习的解方程有何异同? 2.如何用等式的性质解形如a±b=c之类的方程?第一步干什么?第二步干什么? 3.如何检验解形如a±b=c这类方程的正确性? 通过反思总结,理清教师提出的问题。 培养学生反思概括能力和语言表达能力。
板书 设计
教学 反思
学习内容 教科书第84页例3及课堂活动第1、2题,练习二十四第4~6题。
育人目标 1.结合具体情景,认识形如a±b=c这类方程,理解其现实意义。 2.探究并理解解形如a±b=c这类方程的基本思路,能用等式的性质解这类方程。 3.会检验形如a±b=c这类方程解方程的结果。
学习重难点 重点:能用等式的性质解形如a±b=c这类方程。 难点:探究并理解解形如a±b=c这类方程的基本思路。
教学过程
环节 教师活动 学生活动 五育融合育人点提示
复习引入 1.解方程,并说说解方程的依据和过程。 -27=33 ÷12=5 2.前面我们学习了解方程,今天继续学习解方程。(板书课题:解方程) 1.完成解方程。
教学新课 1.教学例3。 (1)出示例3:解方程5y-8=12。 (2)怎么解这个方程? 汇报:第一种解法(四则运算各部分之间的关系) 5y-8=12 解: 5y=12+8 (把5y看成是一个整体,根据被减数=差+减法) 5y=20 y=20÷5(一个因数=积÷另一个因数) y=4 第二种解法:(重点评议用等式的性质解方程的思路,规范解方程的书写格式。) 5y-8=12 解:5y-8+8=12+8(方程两边都加8) 5y=20 5y÷5=20÷5(方程两边都除以5) y=4 第一步,为什么要方程的两边都加8? 第二步,为什么要方程的两边都除以5? ④归纳小结。 对比:两种解法有什么不同? 强调:解像5y-8=12这种方程,既可以根据加、减、乘、除各部分之间的关系来解,也可以用等式的性质来解,但是为了以后能解更复杂的方程,我们提倡用等式的性质来解。 (3)解得对不对?怎么验算呢? 检验:把y=4代入原方程, 左边=5×4-8 =20-8 =12=右边 所以y=4是原方程的解。 (4)回顾总结:今天学习的解方程与前面学习的解方程有什么不同点和相同点? 不同点:计算步骤不同。 相同点:都是用等式的性质来解方程;书写格式相同;检验的方法相同。 (5)完成例3下面的“试一试”。 解方程:18+6=30 4n-2.5×4=15 部分学生解第二个方程可能有困难,可以让学生先思考,这个方程与前面学习的方程有什么不同?应该先这么办?让学生明确先算出2.5×4的积,就变成了学过的方程的类型。 学生独立思考,自己尝试解决,再小组合作交流,最后汇报评议。 2.理解两种解法的依据。 3.验算。 4.回顾总结并完成“试一试”,再集体评议。 在多元方法的论证过程中,培养学生的数学结合思想,感受数学方法的多元化。 在验证的过程中,培养学生的严谨意识。
应用练习 1.完成第84页课堂活动第1、2题。 2.练习二十四第4、5题。 (1)学生先独立列方程,评议。 (2)学生独立解方程,评议。 3.独立完成练习二十四第6题。 学生独立完成,再集体评议。 及时练习,培养学生知识的应用能力。
反思总结 今天学习了什么?谈谈你的收获。 1.今天学习的解方程与前面学习的解方程有何异同? 2.如何用等式的性质解形如a±b=c之类的方程?第一步干什么?第二步干什么? 3.如何检验解形如a±b=c这类方程的正确性? 通过反思总结,理清教师提出的问题。 培养学生反思概括能力和语言表达能力。
板书 设计
教学 反思
