江西省赣州市赣县区三高2021-2022学年高二下学期2月开学考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 江西省赣州市赣县区三高2021-2022学年高二下学期2月开学考试数学(理)试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 20:08:15 | ||
图片预览



文档简介
赣县区三高2021-2022学年高二下学期2月开学考试
理数试卷
一、单选题
1.已知动圆⊙经过定点,且和直线相切,则点的轨迹方程为( )
A. B. C. D.
2.下图是一个边长为4的正方形二维码,为了测算图中黑色部分的面积,在正方形区域内随机投掷400个点,其中落入黑色部分的有225个点,据此可估计黑色部分的面积为( )
A.8 B.9 C.10 D.12
3.以双曲线的右焦点为圆心且与双曲线的渐近线相切的圆的方程是( )
A. B.
C. D.
4.国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
A.12个月的PMI值不低于50%的频率为
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
5.某同学为了求,设计了如图所示的程序框图,在该程序框图中,①和②两处应分别填入( )
A. B.
C. D.
6.某学校对高三年级500名学生进行系统抽样,编号分别为001,002,…,500,若样本相邻的两个编号为031,056,则样本中编号最大的为( )
A.479 B.480 C.481 D.482
7.已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A. B. C. D.
8.设,分别为双曲线的左,右焦点,点为双曲线上的一点.若,则点到轴的距离为( )
A. B. C. D.
9.如图,直三棱柱ABC一中,侧棱长为2,,,D是的中点,F是上的动点,,DF交于点E,要使平面,则线段的长为( )
A. B. C. D.
10.是椭圆上的一点,为左顶点,为右焦点,轴,若,则椭圆的离心率为( )
A. B. C. D.
11.有一凸透镜其剖面图(如图)是由椭圆和双曲线的实线部分组成,已知两曲线有共同焦点、;、分别在左右两部分实线上运动,则周长的最小值为( )
A. B.
C. D.
12.下列命题中,结论为真命题的组合是( )
①“”是“直线与直线相互垂直”的充分而不必要条件
②若命题“”为假命题,则命题一定是假命题
③是的必要不充分条件
④双曲线被点平分的弦所在的直线方程为
⑤已知过点的直线与圆的交点个数有2个.
A.①③④ B.②③④ C.①③⑤ D.①②⑤
二、填空题
13.设直线的方向向量分别为,,若,则实数______.
14.将一块正方形纸片先按如图1所示的阴影部分截去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个体积为的四棱锥模型,该四棱锥底面是正方形,从顶点向底面作垂线,垂足是底面中心.将该四棱锥如图2放置,若其正视图为正三角形,则正方形纸片的边长为__ ____.
15.给出如下四个命题:
①“抛物线的焦点坐标是”为真命题;
②若:,则:;
③“,”的否定是“,”;
④“任意,”为真命题的一个充分不必要条件是.
其中不正确的命题的是 ___________.
16.已知椭圆,若此椭圆上存在不同的两点,关于直线对称,则实数的取值范围是___________.
三、解答题
17.已知命题:方程表示焦点在轴上的椭圆,命题:,不等式恒成立.
(1)若“”是真命题,求实数的取值范围;
(2)若“”为假命题,“”为真命题,求实数的取值范围.
18.新冠肺炎疫情发生以来,我国某科研机构开展应急科研攻关,研制了一种新型冠状病毒疫苗,并已进入二期临床试验.根据普遍规律,志愿者接种疫苗后体内会产生抗体,人体中检测到抗体,说明有抵御病毒的能力.通过检测,用表示注射疫苗后的天数,表示人体中抗体含量水平(单位:,即:百万国际单位/毫升),现测得某志愿者的相关数据如下表所示:
天数 1 2 3 4 5 6
抗体含量水平 5 10 26 50 96 195
根据以上数据,绘制了散点图.
(1)根据散点图判断,与(a,b,c,d均为大于0的实数)哪一个更适宜作为描述y与x关系的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果求出y关于x的回归方程,并预测该志愿者在注射疫苗后的第10天的抗体含量水平值;
(3)从这位志愿者的前6天的检测数据中随机抽取4天的数据作进一步的分析,求其中的y值大于50的天数为1的概率.
参考数据:
3.50 63.67 3.49 17.50 9.49 12.95 519.01 4023.87
其中.参考公式:用最小二乘法求经过点,,,,的线性回归方程的系数公式,;.
19.如图,三棱锥的底面是边长为2的正三角形,侧面底面,且侧面为菱形,,是的中点,是与的交点.
(1)求证:底面;
(2)求与平面所成角的正弦值.
20.已知椭圆 的离心率为,长轴长为,直线与椭圆交于、两点且为直角,为坐标原点.
(1)求椭圆的方程;
(2)求的长度.
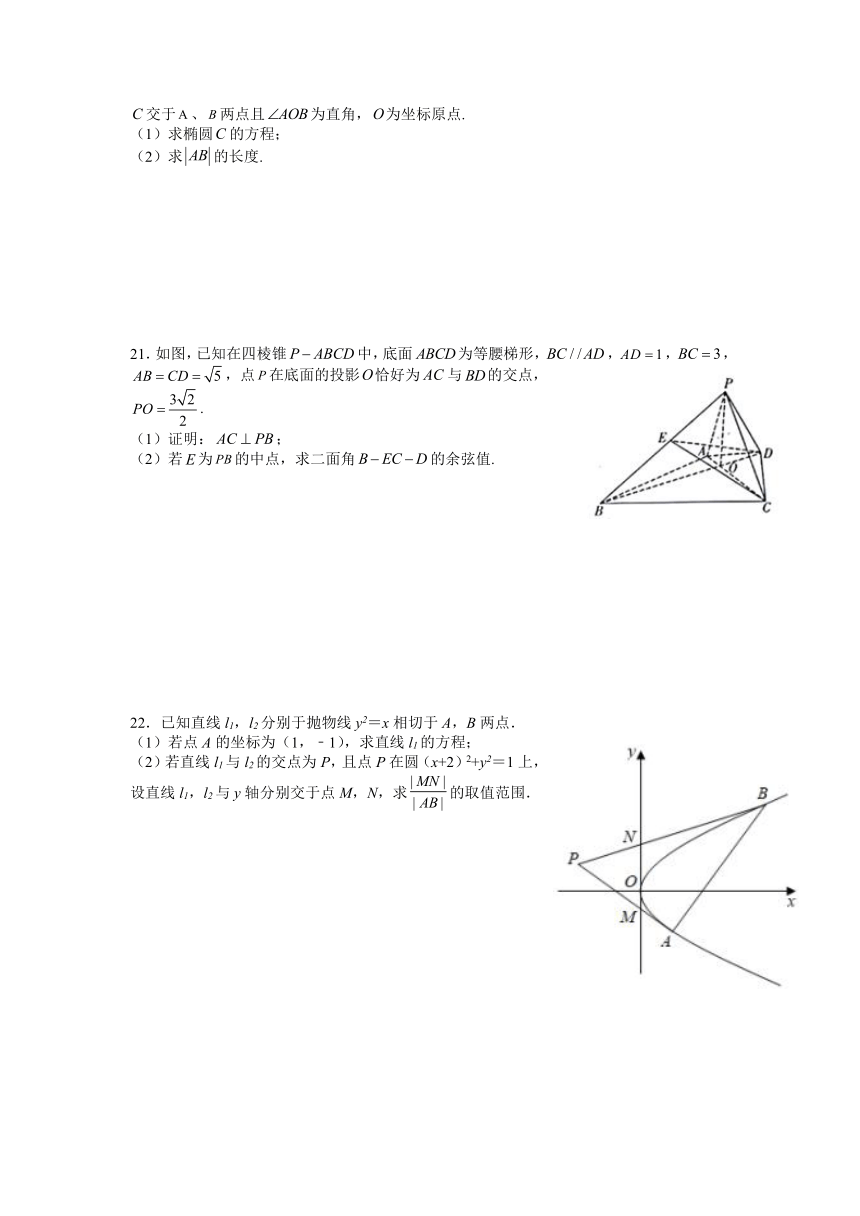
21.如图,已知在四棱锥中,底面为等腰梯形,,,,,点在底面的投影恰好为与的交点,.
(1)证明:;
(2)若为的中点,求二面角的余弦值.
22.已知直线l1,l2分别于抛物线y2=x相切于A,B两点.
(1)若点A的坐标为(1,﹣1),求直线l1的方程;
(2)若直线l1与l2的交点为P,且点P在圆(x+2)2+y2=1上,设直线l1,l2与y轴分别交于点M,N,求的取值范围.
赣县区三高2021-2022学年高二下学期2月开学考试
理数答案
1-12 BBCDCC BCCDBC
13. 14.6 15.①②③④ 16.
17.【详解】
(1)因为,不等式恒成立,
所以,解得,又“”是真命题等价于“”是假命题.
所以所求实数的取值范围是
(2)方程表示焦点在轴上的椭圆,
“”为假命题,“”为真命题,
一个为真命题,一个为假命题,
当真假时, 则,此时无解.
当假真时,则,此时或
综上所述,实数的取值范围是
;.
18.(1)根据散点图可知这些点分布在一条曲线的附近,所以更适合作为描述y与x关系的回归方程类型.
(2)设,变换后可得,设,建立w关于x的回归方程,
,所以
所以w关于x的回归方程为,所以,
当时,,
即该志愿者在注射疫苗后的第10天的抗体含量水平值约为4023.87miu/mL.
(3)由表格数据可知,第5,6天的y值大于50,
19【详解】(1)取的中点,连接,
∵是与的交点,且侧面为菱形
∴是的中点∴
∵底面,底面
∴底面
∵,,为中点
∴,
∴四边形为平行四边形
∴
又底面,底面,
∴底面
∵,平面,平面
∴平面底面
∵平面
∴底面
(2)解:连接,∵侧面为菱形,
∴为正三角形∴
∵侧面底面,侧面底面,侧面
∴底面
∵底面为正三角形,为的中点
∴
以为坐标原点,分别以,,的方向为轴,轴,轴的正方向,建立如图所示的空间直角坐标系.
∵底面是边长为2的正三角形
∴,,,
∴,,
设平面的一个法向量为
由得,令,得
∴
∴.
方法二:(向量法),其中是直线的方向向量,是平面的法向量,是直线和平面所成的角.
20【详解】(1)由题意, ,
所以.椭圆方程为
(2)设,,把代人,得.
因为为直角,所以,
得,,所以,
,
.
∴的长度为
21【详解】(1)证明:如图,在平面图形中,过点作的垂线交于点,
易得,故,
在中,由余弦定理知,
,
故.
由相似可知,,
又,∴,
故,∴.
又点在底面的投影为,∴平面,∴,
又,∴平面,∴.
(2)解:如图,以为原点,,,分别为,,轴
建立空间直角坐标系,由(1)知,
故,,,
,,,
故,,.
设平面的一个法向量为,
则,即,
令,解得,故.
同理,可求得平面的一个法向量为,
设二面角为,
则.
22.【详解】(1)由题意知直线l1,l2的斜率一定存在,设直线l1:y+1=k(x﹣1),与抛物线方程联立,得ky2﹣y﹣k﹣1=0.
由△=1+4k(k+1)=0,得,则l1的方程为.
(2)设A(x1,y1),B(x2,y2),设直线l1: ,与抛物线方程y2=x联立,得.
由 ,解得,所以直线,同理得直线,则,.
设点P(x0,y0),代入可得,则直线AB方程为.
与抛物线方程联立,得y2﹣2y0y+x0=0,则有y1+y2=2y0,y1y2=x0.
则,,所以.
又点P在圆(x+2)2+y2=1上,所以,即,所以.
所以的取值范围为.
理数试卷
一、单选题
1.已知动圆⊙经过定点,且和直线相切,则点的轨迹方程为( )
A. B. C. D.
2.下图是一个边长为4的正方形二维码,为了测算图中黑色部分的面积,在正方形区域内随机投掷400个点,其中落入黑色部分的有225个点,据此可估计黑色部分的面积为( )
A.8 B.9 C.10 D.12
3.以双曲线的右焦点为圆心且与双曲线的渐近线相切的圆的方程是( )
A. B.
C. D.
4.国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
A.12个月的PMI值不低于50%的频率为
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
5.某同学为了求,设计了如图所示的程序框图,在该程序框图中,①和②两处应分别填入( )
A. B.
C. D.
6.某学校对高三年级500名学生进行系统抽样,编号分别为001,002,…,500,若样本相邻的两个编号为031,056,则样本中编号最大的为( )
A.479 B.480 C.481 D.482
7.已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A. B. C. D.
8.设,分别为双曲线的左,右焦点,点为双曲线上的一点.若,则点到轴的距离为( )
A. B. C. D.
9.如图,直三棱柱ABC一中,侧棱长为2,,,D是的中点,F是上的动点,,DF交于点E,要使平面,则线段的长为( )
A. B. C. D.
10.是椭圆上的一点,为左顶点,为右焦点,轴,若,则椭圆的离心率为( )
A. B. C. D.
11.有一凸透镜其剖面图(如图)是由椭圆和双曲线的实线部分组成,已知两曲线有共同焦点、;、分别在左右两部分实线上运动,则周长的最小值为( )
A. B.
C. D.
12.下列命题中,结论为真命题的组合是( )
①“”是“直线与直线相互垂直”的充分而不必要条件
②若命题“”为假命题,则命题一定是假命题
③是的必要不充分条件
④双曲线被点平分的弦所在的直线方程为
⑤已知过点的直线与圆的交点个数有2个.
A.①③④ B.②③④ C.①③⑤ D.①②⑤
二、填空题
13.设直线的方向向量分别为,,若,则实数______.
14.将一块正方形纸片先按如图1所示的阴影部分截去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个体积为的四棱锥模型,该四棱锥底面是正方形,从顶点向底面作垂线,垂足是底面中心.将该四棱锥如图2放置,若其正视图为正三角形,则正方形纸片的边长为__ ____.
15.给出如下四个命题:
①“抛物线的焦点坐标是”为真命题;
②若:,则:;
③“,”的否定是“,”;
④“任意,”为真命题的一个充分不必要条件是.
其中不正确的命题的是 ___________.
16.已知椭圆,若此椭圆上存在不同的两点,关于直线对称,则实数的取值范围是___________.
三、解答题
17.已知命题:方程表示焦点在轴上的椭圆,命题:,不等式恒成立.
(1)若“”是真命题,求实数的取值范围;
(2)若“”为假命题,“”为真命题,求实数的取值范围.
18.新冠肺炎疫情发生以来,我国某科研机构开展应急科研攻关,研制了一种新型冠状病毒疫苗,并已进入二期临床试验.根据普遍规律,志愿者接种疫苗后体内会产生抗体,人体中检测到抗体,说明有抵御病毒的能力.通过检测,用表示注射疫苗后的天数,表示人体中抗体含量水平(单位:,即:百万国际单位/毫升),现测得某志愿者的相关数据如下表所示:
天数 1 2 3 4 5 6
抗体含量水平 5 10 26 50 96 195
根据以上数据,绘制了散点图.
(1)根据散点图判断,与(a,b,c,d均为大于0的实数)哪一个更适宜作为描述y与x关系的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果求出y关于x的回归方程,并预测该志愿者在注射疫苗后的第10天的抗体含量水平值;
(3)从这位志愿者的前6天的检测数据中随机抽取4天的数据作进一步的分析,求其中的y值大于50的天数为1的概率.
参考数据:
3.50 63.67 3.49 17.50 9.49 12.95 519.01 4023.87
其中.参考公式:用最小二乘法求经过点,,,,的线性回归方程的系数公式,;.
19.如图,三棱锥的底面是边长为2的正三角形,侧面底面,且侧面为菱形,,是的中点,是与的交点.
(1)求证:底面;
(2)求与平面所成角的正弦值.
20.已知椭圆 的离心率为,长轴长为,直线与椭圆交于、两点且为直角,为坐标原点.
(1)求椭圆的方程;
(2)求的长度.
21.如图,已知在四棱锥中,底面为等腰梯形,,,,,点在底面的投影恰好为与的交点,.
(1)证明:;
(2)若为的中点,求二面角的余弦值.
22.已知直线l1,l2分别于抛物线y2=x相切于A,B两点.
(1)若点A的坐标为(1,﹣1),求直线l1的方程;
(2)若直线l1与l2的交点为P,且点P在圆(x+2)2+y2=1上,设直线l1,l2与y轴分别交于点M,N,求的取值范围.
赣县区三高2021-2022学年高二下学期2月开学考试
理数答案
1-12 BBCDCC BCCDBC
13. 14.6 15.①②③④ 16.
17.【详解】
(1)因为,不等式恒成立,
所以,解得,又“”是真命题等价于“”是假命题.
所以所求实数的取值范围是
(2)方程表示焦点在轴上的椭圆,
“”为假命题,“”为真命题,
一个为真命题,一个为假命题,
当真假时, 则,此时无解.
当假真时,则,此时或
综上所述,实数的取值范围是
;.
18.(1)根据散点图可知这些点分布在一条曲线的附近,所以更适合作为描述y与x关系的回归方程类型.
(2)设,变换后可得,设,建立w关于x的回归方程,
,所以
所以w关于x的回归方程为,所以,
当时,,
即该志愿者在注射疫苗后的第10天的抗体含量水平值约为4023.87miu/mL.
(3)由表格数据可知,第5,6天的y值大于50,
19【详解】(1)取的中点,连接,
∵是与的交点,且侧面为菱形
∴是的中点∴
∵底面,底面
∴底面
∵,,为中点
∴,
∴四边形为平行四边形
∴
又底面,底面,
∴底面
∵,平面,平面
∴平面底面
∵平面
∴底面
(2)解:连接,∵侧面为菱形,
∴为正三角形∴
∵侧面底面,侧面底面,侧面
∴底面
∵底面为正三角形,为的中点
∴
以为坐标原点,分别以,,的方向为轴,轴,轴的正方向,建立如图所示的空间直角坐标系.
∵底面是边长为2的正三角形
∴,,,
∴,,
设平面的一个法向量为
由得,令,得
∴
∴.
方法二:(向量法),其中是直线的方向向量,是平面的法向量,是直线和平面所成的角.
20【详解】(1)由题意, ,
所以.椭圆方程为
(2)设,,把代人,得.
因为为直角,所以,
得,,所以,
,
.
∴的长度为
21【详解】(1)证明:如图,在平面图形中,过点作的垂线交于点,
易得,故,
在中,由余弦定理知,
,
故.
由相似可知,,
又,∴,
故,∴.
又点在底面的投影为,∴平面,∴,
又,∴平面,∴.
(2)解:如图,以为原点,,,分别为,,轴
建立空间直角坐标系,由(1)知,
故,,,
,,,
故,,.
设平面的一个法向量为,
则,即,
令,解得,故.
同理,可求得平面的一个法向量为,
设二面角为,
则.
22.【详解】(1)由题意知直线l1,l2的斜率一定存在,设直线l1:y+1=k(x﹣1),与抛物线方程联立,得ky2﹣y﹣k﹣1=0.
由△=1+4k(k+1)=0,得,则l1的方程为.
(2)设A(x1,y1),B(x2,y2),设直线l1: ,与抛物线方程y2=x联立,得.
由 ,解得,所以直线,同理得直线,则,.
设点P(x0,y0),代入可得,则直线AB方程为.
与抛物线方程联立,得y2﹣2y0y+x0=0,则有y1+y2=2y0,y1y2=x0.
则,,所以.
又点P在圆(x+2)2+y2=1上,所以,即,所以.
所以的取值范围为.
同课章节目录
