江西省赣州市赣县区三高2021-2022学年高一下学期2月开学考试数学试题(Word版含答案)
文档属性
| 名称 | 江西省赣州市赣县区三高2021-2022学年高一下学期2月开学考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 935.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 20:08:34 | ||
图片预览



文档简介
赣县区三高2021-2022学年高一下学期2月开学考试
数学试卷
考试时间:120分钟;
一、选择题(1-8为单选题,9-12为多选题)
1.已知集合,,则( )
A. B. C. D.
2.命题“存在一个无理数,它的平方是有理数”的否定是( )
A.任意一个无理数,它的平方不是有理数 B.任意一个无理数,它的平方是有理数
C.存在一个无理数,它的平方是有理数 D.存在一个无理数,它的平方不是有理数
3.下列说法正确的为( )
A.
B.函数的最小值为4
C.若则最大值为1
D.已知时,,当且仅当即时,取得最小值8
4.若关于x的不等式的解集为.则关于x的不等式的解集为( )
A. B. C. D.
5.设,定义运算和如下:,.若正数,,,满足,,则( )
A. B.
C. D.
6.已知函数若(,,,互不相等),则的取值范围是( )
A. B. C. D.
7.已知是定义在上的偶函数,是定义在上的奇函数,则的值为( )
A.-1 B.0 C.1 D.无法计算
8.已知是函数的两个零点,则( )
A. B. C. D.
9.(多选)给出以下26个数据:
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0
158.0 158.0 159.0 159.0 161.0 162.0 162.5 162.5 163.0
163.0 163.0 164.0 164.0 165.0 170.0 171.0 172.0
对于以上给出的数据,下列选项正确的为( )
A.众数为163.0 B.第25百分位数为155.0
C.中位数为160.0 D.80%位数为164.0
10.(多选)同学们,你们是否注意到;自然下垂的铁链;空旷田野上,两根电线杆之间的电线;峡谷的上空,横跨深涧的观光索道的钢索.这些现象中都有相似的曲线形态.这些曲线在数学上常常被称为悬链线.悬链线相关理论在工程 航海 光学等方面有广泛的应用.在恰当的坐标系中,这类函数表达式可以为(其中a,b是非零常数,无理数e=2.71828…),对于函数,以下结论正确的是( )
A.如果a=b,那么为奇函数 B.如果,那么为单调函数
C.如果,那么没有零点 D.如果,那么的最小值为2
11.(多选)若函数在上的最大值为M,最小值为m,则( )
A. B. C. D.
12.(多选)先后两次郑一枚质地均匀的骰子,表示事件“两次郑出的点数之和是5”,表示事件“第二次掷出的点数是偶数”,表示事件“第一次掷出的点数是5”,表示事件“至少出现一个奇数点”,则( )
A.与互斥 B. C.与对立 D.与相互独立
二、填空题
13.若,则的最大值是_________.
14.若函数同时满足:(i)为偶函数;(ii)对任意且,总有;(iii)定义域为,值域为,则称函数具有性质,现有个函数:①,②,③,④,其中具有性质的是___________(填上所有满足条件的序号).
15.已知函数,若,则实数的取值范围是___________.
16.函数的值域为____ __.
四、解答题
17.已知集合,.
(1)若,求;
(2)若,求a的取值集合.
18.已知函数,.
(1)证明:函数在上单调递增;
(2)若,求实数t的取值范围.
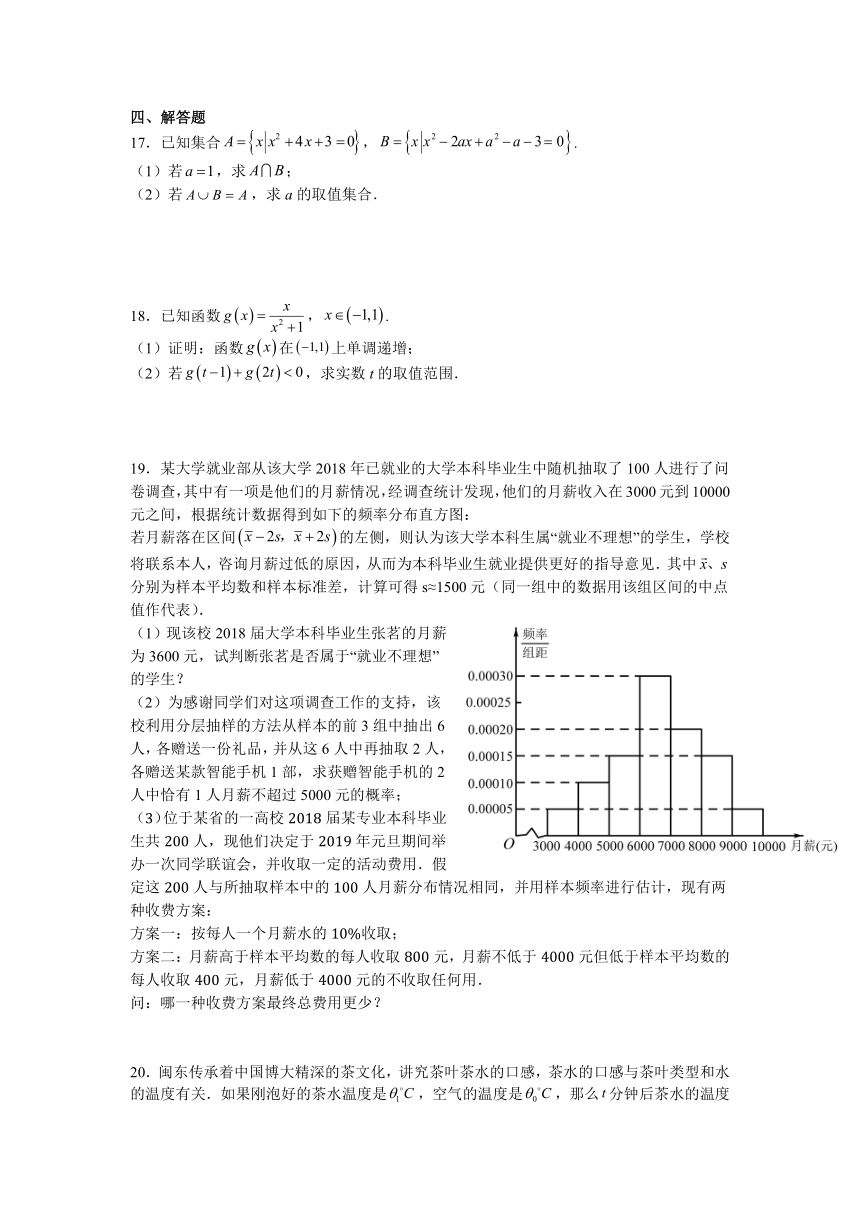
19.某大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行了问卷调查,其中有一项是他们的月薪情况,经调查统计发现,他们的月薪收入在3000元到10000元之间,根据统计数据得到如下的频率分布直方图:
若月薪落在区间的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中分别为样本平均数和样本标准差,计算可得s≈1500元(同一组中的数据用该组区间的中点值作代表).
(1)现该校2018届大学本科毕业生张茗的月薪为3600元,试判断张茗是否属于“就业不理想”的学生?
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽出6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5000元的概率;
(3)位于某省的一高校2018届某专业本科毕业生共200人,现他们决定于2019年元旦期间举办一次同学联谊会,并收取一定的活动费用.假定这200人与所抽取样本中的100人月薪分布情况相同,并用样本频率进行估计,现有两种收费方案:
方案一:按每人一个月薪水的10%收取;
方案二:月薪高于样本平均数的每人收取800元,月薪不低于4000元但低于样本平均数的每人收取400元,月薪低于4000元的不收取任何用.
问:哪一种收费方案最终总费用更少?
20.闽东传承着中国博大精深的茶文化,讲究茶叶茶水的口感,茶水的口感与茶叶类型和水的温度有关.如果刚泡好的茶水温度是,空气的温度是,那么分钟后茶水的温度(单位:)可由公式求得,其中是一个物体与空气的接触状况而定的正常数.现有某种刚泡好的红茶水温度是,放在的空气中自然冷却,10分钟以后茶水的温度是.
(1)求k的值;
(2)经验表明,温度为 的该红茶水放在的空气中自然冷却至时饮用,可以产生最佳口感,那么,大约需要多长时间才能达到最佳饮用口感
(结果精确到,附:参考值)
21.已知,函数.
(1)判断函数的奇偶性,请说明理由;
(2)设,求函数在区间上的最小值.
22.设函数是定义域为R的奇函数.
(1)求;
(2)若,求使不等式对一切恒成立的实数k的取值范围;
(3)若函数的图象过点,是否存在正数,使函数在上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
赣县区三高2021-2022学年高一下学期2月开学考试
数学参考答案
1.B 2.A 3.C 4.B 5.D 6.D 7.B 8.A
第4题解析:因为不是不等式的解,
所以不等式等价于,
所以或,解得或.
第7题解析:因为是定义在上的奇函数, .
因为是定义在上的偶函数,所以,
可得
所以,因此
9.ACD 10.BC 11.AC 12.ABD
13. 14.① ③ 15. 16.
由己知得,,,构造函数,则在上单调递增,即可得,因为,,所以,所以
17.(1)当时,.因为,
所以.
(2)因为,所以.
当时,解得,,符合题意;
当,即时,,符合题意;
当,即时,,
则解得.,综上,a的取值集合是或.
18.(1)证明:设,且,
则,
∵,,,,
∴,即,∴函数在上单调递增.
(2)因为,则为奇函数.
由,得.又因为在上单调递增,则,解得,故实数t的取值范围为.
19.(1)=3500×1000×0.00005+4500×1000×0.00010+5500×1000×0.00015+6500×1000×0.00030
+7500×1000×0.00020+8500×1000×0.00015+9500×1000×0.00005=6650,
-2s=6650-3000=3650>3600,所以张茗属于“就业不理想“的学生.
(2)第一组有1000×0.00005×100=5人,第二组有1000×0.00010×100=10人,第三组有1000×0.00015×100=15人,所以按照分层抽样抽6人时,第一组抽1人,记为A,第二组抽2人,记为B,C,第三组抽3人,记为D,E,F,
从这6人中抽2人共有15种:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F).其中恰有一人月薪不超过5000元的有9种:(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F).
根据古典概型概率公式可得P==.
20.(1)由题意可知,
,其中,
所以,解得
(2)设刚泡好的茶水大约需要放置分钟才能达到最佳饮用口感,
由题意可知,,令,所以,,,所以,
所以刚泡好的茶水大约需要放置分钟才能达到最佳饮用口感.
21.(1)当时,,该函数的定义域为,
则,是上的奇函数,
当时,,,则有,且,即既不是奇函数,也不是偶函数,
所以,当时,是奇函数,当时,是非奇非偶函数;
(2)因,则当时,,当且仅当时取等号,即,
当时且时,,
显然,即在上递增, ;
当时,,对称轴,
①若,即当时,在上单调递增,在上单调递减,
此时,;
②若,即当时,函数在上单调递增,此时.
综上得:.
22.(1)函数是定义域为R的奇函数,
所以,解得,此时,满足;
(2)因为,所以,解得,
所以在R上是减函数,
等价于,
所以,即,
又因为不等式对一切恒成立,
所以对一切恒成立,
所以,解得,所以实数k的取值范围是;
(3)因为函数的图象过点,
所以,解得,
则,
令,则,
当时, 是减函数,,
因为函数在上的最大值为2,所以,即,
解得,不成立;
当时,是增函数,,
因为函数在上的最大值为2,所以,即,
解得或(舍去),
所以存在正数,使函数在上的最大值为2.
数学试卷
考试时间:120分钟;
一、选择题(1-8为单选题,9-12为多选题)
1.已知集合,,则( )
A. B. C. D.
2.命题“存在一个无理数,它的平方是有理数”的否定是( )
A.任意一个无理数,它的平方不是有理数 B.任意一个无理数,它的平方是有理数
C.存在一个无理数,它的平方是有理数 D.存在一个无理数,它的平方不是有理数
3.下列说法正确的为( )
A.
B.函数的最小值为4
C.若则最大值为1
D.已知时,,当且仅当即时,取得最小值8
4.若关于x的不等式的解集为.则关于x的不等式的解集为( )
A. B. C. D.
5.设,定义运算和如下:,.若正数,,,满足,,则( )
A. B.
C. D.
6.已知函数若(,,,互不相等),则的取值范围是( )
A. B. C. D.
7.已知是定义在上的偶函数,是定义在上的奇函数,则的值为( )
A.-1 B.0 C.1 D.无法计算
8.已知是函数的两个零点,则( )
A. B. C. D.
9.(多选)给出以下26个数据:
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0
158.0 158.0 159.0 159.0 161.0 162.0 162.5 162.5 163.0
163.0 163.0 164.0 164.0 165.0 170.0 171.0 172.0
对于以上给出的数据,下列选项正确的为( )
A.众数为163.0 B.第25百分位数为155.0
C.中位数为160.0 D.80%位数为164.0
10.(多选)同学们,你们是否注意到;自然下垂的铁链;空旷田野上,两根电线杆之间的电线;峡谷的上空,横跨深涧的观光索道的钢索.这些现象中都有相似的曲线形态.这些曲线在数学上常常被称为悬链线.悬链线相关理论在工程 航海 光学等方面有广泛的应用.在恰当的坐标系中,这类函数表达式可以为(其中a,b是非零常数,无理数e=2.71828…),对于函数,以下结论正确的是( )
A.如果a=b,那么为奇函数 B.如果,那么为单调函数
C.如果,那么没有零点 D.如果,那么的最小值为2
11.(多选)若函数在上的最大值为M,最小值为m,则( )
A. B. C. D.
12.(多选)先后两次郑一枚质地均匀的骰子,表示事件“两次郑出的点数之和是5”,表示事件“第二次掷出的点数是偶数”,表示事件“第一次掷出的点数是5”,表示事件“至少出现一个奇数点”,则( )
A.与互斥 B. C.与对立 D.与相互独立
二、填空题
13.若,则的最大值是_________.
14.若函数同时满足:(i)为偶函数;(ii)对任意且,总有;(iii)定义域为,值域为,则称函数具有性质,现有个函数:①,②,③,④,其中具有性质的是___________(填上所有满足条件的序号).
15.已知函数,若,则实数的取值范围是___________.
16.函数的值域为____ __.
四、解答题
17.已知集合,.
(1)若,求;
(2)若,求a的取值集合.
18.已知函数,.
(1)证明:函数在上单调递增;
(2)若,求实数t的取值范围.
19.某大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行了问卷调查,其中有一项是他们的月薪情况,经调查统计发现,他们的月薪收入在3000元到10000元之间,根据统计数据得到如下的频率分布直方图:
若月薪落在区间的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中分别为样本平均数和样本标准差,计算可得s≈1500元(同一组中的数据用该组区间的中点值作代表).
(1)现该校2018届大学本科毕业生张茗的月薪为3600元,试判断张茗是否属于“就业不理想”的学生?
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽出6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5000元的概率;
(3)位于某省的一高校2018届某专业本科毕业生共200人,现他们决定于2019年元旦期间举办一次同学联谊会,并收取一定的活动费用.假定这200人与所抽取样本中的100人月薪分布情况相同,并用样本频率进行估计,现有两种收费方案:
方案一:按每人一个月薪水的10%收取;
方案二:月薪高于样本平均数的每人收取800元,月薪不低于4000元但低于样本平均数的每人收取400元,月薪低于4000元的不收取任何用.
问:哪一种收费方案最终总费用更少?
20.闽东传承着中国博大精深的茶文化,讲究茶叶茶水的口感,茶水的口感与茶叶类型和水的温度有关.如果刚泡好的茶水温度是,空气的温度是,那么分钟后茶水的温度(单位:)可由公式求得,其中是一个物体与空气的接触状况而定的正常数.现有某种刚泡好的红茶水温度是,放在的空气中自然冷却,10分钟以后茶水的温度是.
(1)求k的值;
(2)经验表明,温度为 的该红茶水放在的空气中自然冷却至时饮用,可以产生最佳口感,那么,大约需要多长时间才能达到最佳饮用口感
(结果精确到,附:参考值)
21.已知,函数.
(1)判断函数的奇偶性,请说明理由;
(2)设,求函数在区间上的最小值.
22.设函数是定义域为R的奇函数.
(1)求;
(2)若,求使不等式对一切恒成立的实数k的取值范围;
(3)若函数的图象过点,是否存在正数,使函数在上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
赣县区三高2021-2022学年高一下学期2月开学考试
数学参考答案
1.B 2.A 3.C 4.B 5.D 6.D 7.B 8.A
第4题解析:因为不是不等式的解,
所以不等式等价于,
所以或,解得或.
第7题解析:因为是定义在上的奇函数, .
因为是定义在上的偶函数,所以,
可得
所以,因此
9.ACD 10.BC 11.AC 12.ABD
13. 14.① ③ 15. 16.
由己知得,,,构造函数,则在上单调递增,即可得,因为,,所以,所以
17.(1)当时,.因为,
所以.
(2)因为,所以.
当时,解得,,符合题意;
当,即时,,符合题意;
当,即时,,
则解得.,综上,a的取值集合是或.
18.(1)证明:设,且,
则,
∵,,,,
∴,即,∴函数在上单调递增.
(2)因为,则为奇函数.
由,得.又因为在上单调递增,则,解得,故实数t的取值范围为.
19.(1)=3500×1000×0.00005+4500×1000×0.00010+5500×1000×0.00015+6500×1000×0.00030
+7500×1000×0.00020+8500×1000×0.00015+9500×1000×0.00005=6650,
-2s=6650-3000=3650>3600,所以张茗属于“就业不理想“的学生.
(2)第一组有1000×0.00005×100=5人,第二组有1000×0.00010×100=10人,第三组有1000×0.00015×100=15人,所以按照分层抽样抽6人时,第一组抽1人,记为A,第二组抽2人,记为B,C,第三组抽3人,记为D,E,F,
从这6人中抽2人共有15种:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F).其中恰有一人月薪不超过5000元的有9种:(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F).
根据古典概型概率公式可得P==.
20.(1)由题意可知,
,其中,
所以,解得
(2)设刚泡好的茶水大约需要放置分钟才能达到最佳饮用口感,
由题意可知,,令,所以,,,所以,
所以刚泡好的茶水大约需要放置分钟才能达到最佳饮用口感.
21.(1)当时,,该函数的定义域为,
则,是上的奇函数,
当时,,,则有,且,即既不是奇函数,也不是偶函数,
所以,当时,是奇函数,当时,是非奇非偶函数;
(2)因,则当时,,当且仅当时取等号,即,
当时且时,,
显然,即在上递增, ;
当时,,对称轴,
①若,即当时,在上单调递增,在上单调递减,
此时,;
②若,即当时,函数在上单调递增,此时.
综上得:.
22.(1)函数是定义域为R的奇函数,
所以,解得,此时,满足;
(2)因为,所以,解得,
所以在R上是减函数,
等价于,
所以,即,
又因为不等式对一切恒成立,
所以对一切恒成立,
所以,解得,所以实数k的取值范围是;
(3)因为函数的图象过点,
所以,解得,
则,
令,则,
当时, 是减函数,,
因为函数在上的最大值为2,所以,即,
解得,不成立;
当时,是增函数,,
因为函数在上的最大值为2,所以,即,
解得或(舍去),
所以存在正数,使函数在上的最大值为2.
同课章节目录
