人教A版(2019)必修第一册第二章2.2基本不等式(Word含答案)
文档属性
| 名称 | 人教A版(2019)必修第一册第二章2.2基本不等式(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 777.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 00:00:00 | ||
图片预览




文档简介
人教A版(2019) 必修第一册 第二章 2.2 基本不等式
一、解答题
1.已知,、、为的三个内角,,
(1)求角;
(2)求面积的最大值.
2.某种汽车,购车费用是10万元,第一年维修费是0.2万元,以后逐年递增0.2万元,且每年的保险费、养路费、汽油费等约为0.9万元。则这种汽车使用多少年时,它的年平均费用最小?
3.某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近视地表示为,已知此生产线的年产量最大为210吨.
(Ⅰ) 求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(Ⅱ)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润 最大利润是多少
4.某地开发一片荒地,如图,荒地的边界是以C为圆心,半径为1千米的圆周.已有两条互相垂直的道路OE,OF,分别与荒地的边界有且仅有一个接触点A,B.现规划修建一条新路(由线段MP,,线段QN三段组成),其中点M,N分别在OE,OF上,且使得MP,QN所在直线分别与荒地的边界有且仅有一个接触点P,Q,所对的圆心角为.记∠PCA=(道路宽度均忽略不计).
(1)若,求QN的长度;
(2)求新路总长度的最小值.
5.(1)解不等式;
(2)已知,其中,求的最小值.
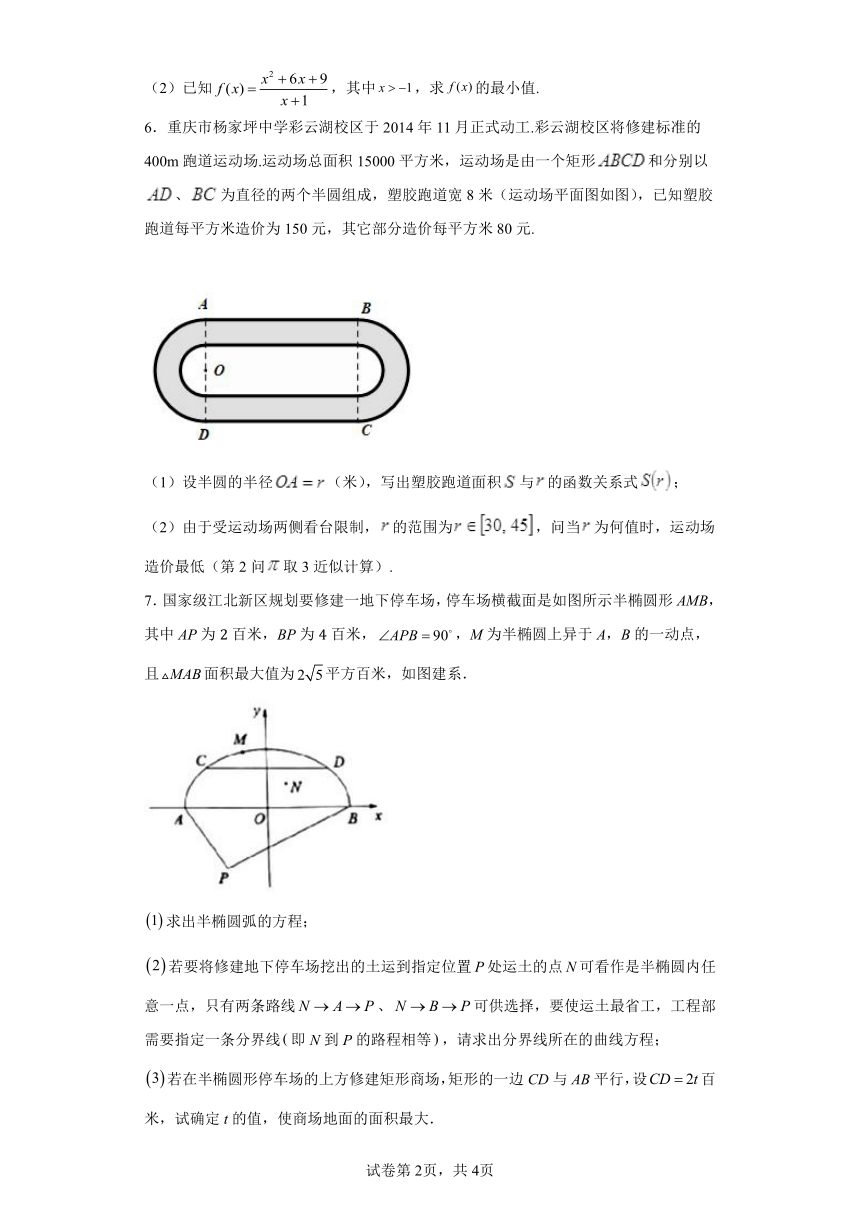
6.重庆市杨家坪中学彩云湖校区于2014年11月正式动工.彩云湖校区将修建标准的400m跑道运动场.运动场总面积15000平方米,运动场是由一个矩形和分别以、为直径的两个半圆组成,塑胶跑道宽8米(运动场平面图如图),已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元.
(1)设半圆的半径(米),写出塑胶跑道面积与的函数关系式;
(2)由于受运动场两侧看台限制,的范围为,问当为何值时,运动场造价最低(第2问取3近似计算).
7.国家级江北新区规划要修建一地下停车场,停车场横截面是如图所示半椭圆形AMB,其中AP为2百米,BP为4百米,,M为半椭圆上异于A,B的一动点,且面积最大值为平方百米,如图建系.
求出半椭圆弧的方程;
若要将修建地下停车场挖出的土运到指定位置P处运土的点N可看作是半椭圆内任意一点,只有两条路线、可供选择,要使运土最省工,工程部需要指定一条分界线即N到P的路程相等,请求出分界线所在的曲线方程;
若在半椭圆形停车场的上方修建矩形商场,矩形的一边CD与AB平行,设百米,试确定t的值,使商场地面的面积最大.
8.设函数,其中,,.
(1)若当时,有最小值,求的最小值;
(2)若,求证:.
9.某天数学课上,你突然惊醒,发现黑板上有如下内容:
例:求的最小值.
解:利用基本不等式,得到, 于是,当且仅当时,取到最小值.
(1)老师请你模仿例题,研究上的最小值;
(提示:)
(2)研究上的最小值;
(3)求出当时,的最小值.
10.已知都是正数,求证:
(1);
(2)若,则.
11.我们知道,,因此,当且仅当时等号成立.即,的算术平均数的平方不大于,平方的算术平均数.请运用这个结论解答下列两题.
(1)求函数的最大值;
(2)已知,,若不等式恒成立,求实数的取值范围.
12.某工厂有旧墙一面,长14米,现在准备利用这面旧墙建造平面图形为矩形 面积为126平方米的厂房,工程条件是:①建1米新墙的费用为元;②修1米旧墙的费用为元;③拆去1米旧墙,用所得的材料建1米新墙的费用为元,经讨论有两种方案:
(1)利用旧墙的一段米为矩形厂房一面的边长;
(2)矩形厂房利用旧墙的一面边长.
问如何利用旧墙,即为多少米时,建造费用最省?(1) (2)两种方案哪个更好?
13.在平面直角坐标系中,点是曲线上的一个动点.
(1)求点的纵坐标的最小值;
(2)求点到直线的距离的最小值.
14.已知的最小值为m.
(1)求m.
(2)若a+b+c=3,证明:.
15.已知为正实数.
(1)求证:;
(2)求的最小值.
16.已知在中,,,分别为角,,所对的边长,且.
(1)求角的值;
(2)若,求的取值范围.
17.在平面直角坐标系中,已知圆过坐标原点且圆心在曲线上.
(1)求圆面积的最小值;
(2)设直线与圆交于不同的两点、,且,求圆的方程;
(3)设直线与(2)中所求圆交于点、,为直线上的动点,直线,与圆的另一个交点分别为,,求证:直线过定点.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1);(2)
【解析】
【分析】
(1)化简f(x),根据f(A)=0.即可求A角;
(2)利用余弦定理建立关系,结合基本不等式的性质即可求解△ABC面积的最大值.
【详解】
(1)由f(x)=sinxcosx=2sin(x﹣60°),
∵f(A)=0.即2sin(A﹣60°)=0,
∵0<A<180°,
可得:A=60°;
(2)由(1)可得A=60°,BC=a=2,
根据余弦定理cosA,
可得bc=b2+c2﹣4,
∵b2+c2≥2bc(当且仅当b=c时取等号),
∴bc+4≥2bc,
可得bc≤4.
那么△ABC面积SbcsinA,
故得△ABC面积的最大值为.
【点睛】
本题考查了三角函数的化简,考查了余弦定理与不等式的结合求解最值问题.属于基础题.
2.10年
【解析】
设使用年平均费用最小,由题意知汽车使用年总维修费用为,设汽车的年平均费用为元,则有,再利用基本不等式求解即可.
【详解】
解:设使用年平均费用最小,
由题意知汽车使用年总维修费用为(万元).
设汽车的年平均费用为元,则有,
当且仅当,即时,取得最小值.
故汽车使用年年平均费用最小.
【点睛】
本题考查基本不等式的应用,属于基础题.
3.(1)年产量为200吨时,每吨平均成本最低为32万元.(2)年产量为210吨时,可获得最大利润1 660万元.
【解析】
【详解】
本题考查将实际问题的最值问题转化为函数的最值问题、考查利用基本不等式求函数的最值需满足:一正、二定、三相等、考查求二次函数的最值关键看对称轴
(1)利用总成本除以年产量表示出平均成本;利用基本不等式求出平均成本的最小值.
(2)利用收入减去总成本表示出年利润;通过配方求出二次函数的对称轴;由于开口向下,对称轴处取得最大值.
解:(1)生产每吨产品的平均成本为
,
由于,
当且仅当时,即时等号成立.
答:年产量为200吨时,每吨平均成本最低为32万元;
(2)设年利润为,则
,
由于在上为增函数,故当
时,的最大值为1660.
答:年产量为210吨时,可获得最大利润1660万元.
4.(1)1千米;(2).
【解析】
【分析】
(1)连接CB,CN,CM,可得,OM,ON,PM,QN均与圆C相切,通过圆心角为可求出∠QCB=,从而得到四边形BCQN是正方形,进而可得QN=CQ=1,
(2)因为∠PCA=,所以∠MCP=,∠NCQ=,利用弧长公式可求得MP=,,NQ=,由于,所以(,),设新路长为,则,然后结合基本不等式进行计算即可得解
【详解】
(1)连接CB,CN,CM,
因为OM⊥ON,所以OM,ON,PM,QN均与圆C相切
所以CB⊥ON,CA⊥OM,CP⊥MP,CQ⊥NQ,
所以CB⊥CA
因为∠PCA=,∠PCQ=,
所以∠QCB=,
此时四边形BCQN是正方形,所以QN=CQ=1,
答:QN的长度为1千米;
(2)∵∠PCA=,可得∠MCP=,∠NCQ=,
则MP=,,NQ=
设新路长为,其中(,),即
∴,
,当时取“=”,
答:新路总长度的最小值为.
【点睛】
本小题主要考查直线和圆的位置关系,考查三角函数在实际生活中的应用,考查基本不等式求最值,考查化归与转化的数学思想方法,属于难题.
5.(1)答案见解析;(2).
【解析】
(1)根据一元二次不等式的解法,分,和,三种情况分类讨论即可求解;
(2)化简,结合基本不等式,即可求解.
【详解】
(1)由题意,不等式 ,
当时,不等式恒成立,解集为,
当时,
若,不等式等价于,
解得或,所以不等式的解集为;
若,不等式等价于,所以不等式的解集为;
若,不等式等价于,
解得或,所以不等式的解集为;
当时,不等式等价于,
解得,所以不等式的解集为.
综上可得:当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
(2)由,可得,,
则,
当且仅当时,即时,等号成立,
综上可得,函数的最小值为.
【点睛】
解含参数的一元二次不等式的步骤:
(1)若二次项含有参数,应先讨论参数是等于0、小于0,还是大于0,然后整理不等式;
(2)当二次项系数不为0时,讨论判别式与0的关系,判断方程的根的个数;
(3)确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集的形式.
6.(1);(2)
【解析】
【详解】
试题分析:(1)
(2)总造价:
∴易知函数在区间上单调递减,故当时,总造价最低.
考点:建立函数模型,求函数的最值
点评:审清题意,合理建立数学模型,利用函数的单调性求函数的最值
7.椭圆弧的方程为;曲线方程为; .
【解析】
【分析】
设椭圆方程为由已知易求出AB=2a的长,结合其他已知条件,列式求得a,b,可得椭圆方程;
由N到P的路程相等,可得,即,故点N在以A,B为焦点的双曲线上,采用定义法即可求得曲线方程;
由且点C,D在椭圆弧上,结合矩形面积公式,得函数式然后利用基本不等式求最值,进而问题得解.
【详解】
在直角三角形PAB中,,,
由勾股定理得:.
设椭圆方程为.
由题意得,解得,.
椭圆弧的方程为;
由点N到P的路程相等,,即.
得,在以A,B为焦点的双曲线上,
设双曲线方程为,
则,解得,.
双曲线方程为;
由,设,则.
.
商场地面积为.
,,
则.
当且仅当,即时“”成立.
当时,商场地面的面积最大为平方百米.
【点睛】
本题考查了与圆锥曲线有关的实际问题,考查了椭圆与双曲线标准方程的求法,考查了利用基本不等式求最值;在实际应用题的解题过程中,要注意自变量的取值范围需符合实际.
8.(1)
(2)证明见解析.
【解析】
【分析】
(1)由在处,有最小值,可知对称轴为,列出关系式,化简可得,利用基本不等式1的应用,代入求出最小值.(2)代入化简可得,两边平方,结合重要不等式可证明.
(1)
解:因为当时,有最小值,所以且对称轴,即,(,)所以
,当且仅当时等号成立. 的最小值为.
(2)
解:,化简得:,
所以,
所以.
9.(1);(2);(3).
【解析】
【分析】
(1)根据新定义可得,求解即可;
(2)根据新定义可得,求解即可;
(3)根据新定义可得,求解即可.
【详解】
(1)由,
知,
当且仅当时,取到最小值;
(2)由,
知
当且仅当时,取到最小值;
(3)由,
知;
当且仅当时,取到最小值.
【点睛】
易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.
10.(1)证明见解析;
(2)证明见解析.
【解析】
【分析】
(1)运用作差法,进而展开、分组,然后提公因式、配方,最后证明问题;
(2)根据题意得到,进而乘出化简,然后通过基本不等式证明问题.
(1)
,
∵都是正数,∴,
当且仅当“”时等号成立,∴.
(2)
,
当且仅当“”时等号成立,∴.
11.(1);(2).
【解析】
【分析】
(1)由,可得,化简变形后可求出的最大值;
(2)由于,变形后可得,而恒成立恒成立,从而可求出实数的取值范围.
【详解】
(1)当时,有,
即,当且仅当,即时等号成立.
而,故函数的最大值为.
(2)当,时,有,所以
即,当且仅当时等号成立.因此的最小值为.
恒成立恒成立.
故实数的取值范围是.
12.采用第(1)种方案,利用旧墙米为矩形的一面边长时,建墙总费用最省,为元.
【解析】
【分析】
以建造总费用为目标函数,把方案(1)和(2)的函数关系式求出来,通过函数求最小值来解决问题
【详解】
利用旧墙的一面矩形边长为x米,则矩形的另一面边长为米,
方案(1):利用旧墙的一段x米,(x<14)为矩形一面边长,则修旧墙费用为元,将剩余旧墙拆得的材料建设新墙的费用为元,其余建新墙的费用为元,故总费用为,利用基本不等式可得:,当且仅当,即时,等号成立,即;
方案(2)若利用旧墙的一面矩形边长,则修旧墙的费用为元,建新墙的费用为元,故总费用,设,则
,因为,所以,,从而,所以函数在上为增函数,故当时,.
综上所述,采用第(1)种方案,利用旧墙12米为矩形的一面边长时,建墙总费用最省,为元.
13.(1)2;
(2)2.
【解析】
【分析】
(1)由基本不等式求得函数的最小值,即点的纵坐标的最小值;
(2)设点P的坐标,由点到直线的距离公式及基本不等式即可得解.
(1)
因为,所以,当且仅当时等号成立,
故得到函数最小值为
点的纵坐标的最小值
(2)
设点,
则点到直线的距离,
因为,所以,当且仅当时,等号成立,
所以点到直线的距离的最小值2.
14.(1)9
(2)证明见解析
【解析】
【分析】
(1)分类讨论求出f(x)的分段函数解析式,求f(x)值域即可;
(2)两边平方结合基本不等式求出最小值,展开即可求其最小值.
(1)
∵
∴当时,;
当时,;
当时,;
∴函数的最小值为9,即m=9.
(2)
由(1)知,即证,
∵,
∴,
即,
∴.
15.(1)证明见解析;(2)3.
【解析】
【分析】
(1)直接利用基本不等式即可证明;
(2)原等式化简可得,由(1)的结论,即可得到答案.
【详解】
(1)因为,由基本不等式可得,,,三式相乘可得:,当且仅当时,等号成立.
(2),
由(1)可得,当且仅当时,取最小值为3.
【点睛】
本题考查基本不等式在证明不等式成立以及求最小值中的应用,在利用基本不等式时,注意使用的前提条件,属于中档题
16.(1);(2).
【解析】
【详解】
试题分析:第一步利用正弦定理进行“边转角”化为三角函数关系,借助两角和公式进行恒等变形,求出角A的余弦值,进而求出角A;第二步利用余弦定理,转化为b+c与bc的关系,然后利用基本不等式“等转不等”,求出b+c的范围,再根据三角形两边之和大于第三边,求出范围.
试题解析:
(1)依题意由正弦定理可得:
又.
(2)由余弦定理知:
(当且仅当时成立)
,又
故的取值范围是.
【点睛】有关解斜三角形问题,常用正弦定理、余弦定理、面积公式等,多用正弦定理和余弦定理进行“边角转化”,求范围或最值问题常用方法有两种,第一边化角,利用三角函数式恒等变形转化为某个角的三角函数式,根据角的范围研究函数值的范围,另一种方法是化边,利用基本不等式求范围或最值.
17.(1)(2)(3)证明见解析;
【解析】
【分析】
(1)由题意设圆心为,半径,利用基本不等式求出半径的最小值,从而得到面积的最小值;
(2)由,知,运用两直线垂直的条件:斜率之积为,解方程可得,讨论的取值,求得圆心到直线的距离的距离,即可得到所求圆的方程;
(3)设,,,求得,的坐标,和的方程,联立圆的方程,运用韦达定理,.设,则.设直线的方程为,代入圆的方程,运用韦达定理,可得,的关系,即可得到所求定点.
【详解】
解:(1)由题意可设圆的圆心为,
则半径为(当且仅当时取等号),
所以圆的面积最小值为.
(2)由,知.
所以,解得.
当时,圆心到直线的距离小于半径,符合题意;
当时,圆心到直线的距离大于半径,不符合题意.
所以,所求圆的方程为.
(3)设,,,又知,,
所以,.
显然,设,则.
从而直线方程为:,
与圆的方程联立,
消去,可得:,
所以,,即;
同理直线方程为:,
与圆的方程联立,
消去,可得:,
所以,,即.
所以;
.
消去参数整理得. ①
设直线的方程为,代入,
整理得.
所以,.
代入①式,并整理得,
即,解得或.
当时,直线的方程为,过定点;
当时,直线的方程为,过定点
第二种情况不合题意(因为,在直径的异侧),舍去.
所以,直线过定点.
【点睛】
本题考查圆的方程的求法和运用,注意运用联立直线方程和圆的方程,消去一个未知数,运用韦达定理,考查直线方程的运用和恒过定点的求法,考查运算能力,属于难题.
答案第1页,共2页
答案第1页,共2页
一、解答题
1.已知,、、为的三个内角,,
(1)求角;
(2)求面积的最大值.
2.某种汽车,购车费用是10万元,第一年维修费是0.2万元,以后逐年递增0.2万元,且每年的保险费、养路费、汽油费等约为0.9万元。则这种汽车使用多少年时,它的年平均费用最小?
3.某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近视地表示为,已知此生产线的年产量最大为210吨.
(Ⅰ) 求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(Ⅱ)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润 最大利润是多少
4.某地开发一片荒地,如图,荒地的边界是以C为圆心,半径为1千米的圆周.已有两条互相垂直的道路OE,OF,分别与荒地的边界有且仅有一个接触点A,B.现规划修建一条新路(由线段MP,,线段QN三段组成),其中点M,N分别在OE,OF上,且使得MP,QN所在直线分别与荒地的边界有且仅有一个接触点P,Q,所对的圆心角为.记∠PCA=(道路宽度均忽略不计).
(1)若,求QN的长度;
(2)求新路总长度的最小值.
5.(1)解不等式;
(2)已知,其中,求的最小值.
6.重庆市杨家坪中学彩云湖校区于2014年11月正式动工.彩云湖校区将修建标准的400m跑道运动场.运动场总面积15000平方米,运动场是由一个矩形和分别以、为直径的两个半圆组成,塑胶跑道宽8米(运动场平面图如图),已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元.
(1)设半圆的半径(米),写出塑胶跑道面积与的函数关系式;
(2)由于受运动场两侧看台限制,的范围为,问当为何值时,运动场造价最低(第2问取3近似计算).
7.国家级江北新区规划要修建一地下停车场,停车场横截面是如图所示半椭圆形AMB,其中AP为2百米,BP为4百米,,M为半椭圆上异于A,B的一动点,且面积最大值为平方百米,如图建系.
求出半椭圆弧的方程;
若要将修建地下停车场挖出的土运到指定位置P处运土的点N可看作是半椭圆内任意一点,只有两条路线、可供选择,要使运土最省工,工程部需要指定一条分界线即N到P的路程相等,请求出分界线所在的曲线方程;
若在半椭圆形停车场的上方修建矩形商场,矩形的一边CD与AB平行,设百米,试确定t的值,使商场地面的面积最大.
8.设函数,其中,,.
(1)若当时,有最小值,求的最小值;
(2)若,求证:.
9.某天数学课上,你突然惊醒,发现黑板上有如下内容:
例:求的最小值.
解:利用基本不等式,得到, 于是,当且仅当时,取到最小值.
(1)老师请你模仿例题,研究上的最小值;
(提示:)
(2)研究上的最小值;
(3)求出当时,的最小值.
10.已知都是正数,求证:
(1);
(2)若,则.
11.我们知道,,因此,当且仅当时等号成立.即,的算术平均数的平方不大于,平方的算术平均数.请运用这个结论解答下列两题.
(1)求函数的最大值;
(2)已知,,若不等式恒成立,求实数的取值范围.
12.某工厂有旧墙一面,长14米,现在准备利用这面旧墙建造平面图形为矩形 面积为126平方米的厂房,工程条件是:①建1米新墙的费用为元;②修1米旧墙的费用为元;③拆去1米旧墙,用所得的材料建1米新墙的费用为元,经讨论有两种方案:
(1)利用旧墙的一段米为矩形厂房一面的边长;
(2)矩形厂房利用旧墙的一面边长.
问如何利用旧墙,即为多少米时,建造费用最省?(1) (2)两种方案哪个更好?
13.在平面直角坐标系中,点是曲线上的一个动点.
(1)求点的纵坐标的最小值;
(2)求点到直线的距离的最小值.
14.已知的最小值为m.
(1)求m.
(2)若a+b+c=3,证明:.
15.已知为正实数.
(1)求证:;
(2)求的最小值.
16.已知在中,,,分别为角,,所对的边长,且.
(1)求角的值;
(2)若,求的取值范围.
17.在平面直角坐标系中,已知圆过坐标原点且圆心在曲线上.
(1)求圆面积的最小值;
(2)设直线与圆交于不同的两点、,且,求圆的方程;
(3)设直线与(2)中所求圆交于点、,为直线上的动点,直线,与圆的另一个交点分别为,,求证:直线过定点.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1);(2)
【解析】
【分析】
(1)化简f(x),根据f(A)=0.即可求A角;
(2)利用余弦定理建立关系,结合基本不等式的性质即可求解△ABC面积的最大值.
【详解】
(1)由f(x)=sinxcosx=2sin(x﹣60°),
∵f(A)=0.即2sin(A﹣60°)=0,
∵0<A<180°,
可得:A=60°;
(2)由(1)可得A=60°,BC=a=2,
根据余弦定理cosA,
可得bc=b2+c2﹣4,
∵b2+c2≥2bc(当且仅当b=c时取等号),
∴bc+4≥2bc,
可得bc≤4.
那么△ABC面积SbcsinA,
故得△ABC面积的最大值为.
【点睛】
本题考查了三角函数的化简,考查了余弦定理与不等式的结合求解最值问题.属于基础题.
2.10年
【解析】
设使用年平均费用最小,由题意知汽车使用年总维修费用为,设汽车的年平均费用为元,则有,再利用基本不等式求解即可.
【详解】
解:设使用年平均费用最小,
由题意知汽车使用年总维修费用为(万元).
设汽车的年平均费用为元,则有,
当且仅当,即时,取得最小值.
故汽车使用年年平均费用最小.
【点睛】
本题考查基本不等式的应用,属于基础题.
3.(1)年产量为200吨时,每吨平均成本最低为32万元.(2)年产量为210吨时,可获得最大利润1 660万元.
【解析】
【详解】
本题考查将实际问题的最值问题转化为函数的最值问题、考查利用基本不等式求函数的最值需满足:一正、二定、三相等、考查求二次函数的最值关键看对称轴
(1)利用总成本除以年产量表示出平均成本;利用基本不等式求出平均成本的最小值.
(2)利用收入减去总成本表示出年利润;通过配方求出二次函数的对称轴;由于开口向下,对称轴处取得最大值.
解:(1)生产每吨产品的平均成本为
,
由于,
当且仅当时,即时等号成立.
答:年产量为200吨时,每吨平均成本最低为32万元;
(2)设年利润为,则
,
由于在上为增函数,故当
时,的最大值为1660.
答:年产量为210吨时,可获得最大利润1660万元.
4.(1)1千米;(2).
【解析】
【分析】
(1)连接CB,CN,CM,可得,OM,ON,PM,QN均与圆C相切,通过圆心角为可求出∠QCB=,从而得到四边形BCQN是正方形,进而可得QN=CQ=1,
(2)因为∠PCA=,所以∠MCP=,∠NCQ=,利用弧长公式可求得MP=,,NQ=,由于,所以(,),设新路长为,则,然后结合基本不等式进行计算即可得解
【详解】
(1)连接CB,CN,CM,
因为OM⊥ON,所以OM,ON,PM,QN均与圆C相切
所以CB⊥ON,CA⊥OM,CP⊥MP,CQ⊥NQ,
所以CB⊥CA
因为∠PCA=,∠PCQ=,
所以∠QCB=,
此时四边形BCQN是正方形,所以QN=CQ=1,
答:QN的长度为1千米;
(2)∵∠PCA=,可得∠MCP=,∠NCQ=,
则MP=,,NQ=
设新路长为,其中(,),即
∴,
,当时取“=”,
答:新路总长度的最小值为.
【点睛】
本小题主要考查直线和圆的位置关系,考查三角函数在实际生活中的应用,考查基本不等式求最值,考查化归与转化的数学思想方法,属于难题.
5.(1)答案见解析;(2).
【解析】
(1)根据一元二次不等式的解法,分,和,三种情况分类讨论即可求解;
(2)化简,结合基本不等式,即可求解.
【详解】
(1)由题意,不等式 ,
当时,不等式恒成立,解集为,
当时,
若,不等式等价于,
解得或,所以不等式的解集为;
若,不等式等价于,所以不等式的解集为;
若,不等式等价于,
解得或,所以不等式的解集为;
当时,不等式等价于,
解得,所以不等式的解集为.
综上可得:当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为;
当时,不等式的解集为.
(2)由,可得,,
则,
当且仅当时,即时,等号成立,
综上可得,函数的最小值为.
【点睛】
解含参数的一元二次不等式的步骤:
(1)若二次项含有参数,应先讨论参数是等于0、小于0,还是大于0,然后整理不等式;
(2)当二次项系数不为0时,讨论判别式与0的关系,判断方程的根的个数;
(3)确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集的形式.
6.(1);(2)
【解析】
【详解】
试题分析:(1)
(2)总造价:
∴易知函数在区间上单调递减,故当时,总造价最低.
考点:建立函数模型,求函数的最值
点评:审清题意,合理建立数学模型,利用函数的单调性求函数的最值
7.椭圆弧的方程为;曲线方程为; .
【解析】
【分析】
设椭圆方程为由已知易求出AB=2a的长,结合其他已知条件,列式求得a,b,可得椭圆方程;
由N到P的路程相等,可得,即,故点N在以A,B为焦点的双曲线上,采用定义法即可求得曲线方程;
由且点C,D在椭圆弧上,结合矩形面积公式,得函数式然后利用基本不等式求最值,进而问题得解.
【详解】
在直角三角形PAB中,,,
由勾股定理得:.
设椭圆方程为.
由题意得,解得,.
椭圆弧的方程为;
由点N到P的路程相等,,即.
得,在以A,B为焦点的双曲线上,
设双曲线方程为,
则,解得,.
双曲线方程为;
由,设,则.
.
商场地面积为.
,,
则.
当且仅当,即时“”成立.
当时,商场地面的面积最大为平方百米.
【点睛】
本题考查了与圆锥曲线有关的实际问题,考查了椭圆与双曲线标准方程的求法,考查了利用基本不等式求最值;在实际应用题的解题过程中,要注意自变量的取值范围需符合实际.
8.(1)
(2)证明见解析.
【解析】
【分析】
(1)由在处,有最小值,可知对称轴为,列出关系式,化简可得,利用基本不等式1的应用,代入求出最小值.(2)代入化简可得,两边平方,结合重要不等式可证明.
(1)
解:因为当时,有最小值,所以且对称轴,即,(,)所以
,当且仅当时等号成立. 的最小值为.
(2)
解:,化简得:,
所以,
所以.
9.(1);(2);(3).
【解析】
【分析】
(1)根据新定义可得,求解即可;
(2)根据新定义可得,求解即可;
(3)根据新定义可得,求解即可.
【详解】
(1)由,
知,
当且仅当时,取到最小值;
(2)由,
知
当且仅当时,取到最小值;
(3)由,
知;
当且仅当时,取到最小值.
【点睛】
易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.
10.(1)证明见解析;
(2)证明见解析.
【解析】
【分析】
(1)运用作差法,进而展开、分组,然后提公因式、配方,最后证明问题;
(2)根据题意得到,进而乘出化简,然后通过基本不等式证明问题.
(1)
,
∵都是正数,∴,
当且仅当“”时等号成立,∴.
(2)
,
当且仅当“”时等号成立,∴.
11.(1);(2).
【解析】
【分析】
(1)由,可得,化简变形后可求出的最大值;
(2)由于,变形后可得,而恒成立恒成立,从而可求出实数的取值范围.
【详解】
(1)当时,有,
即,当且仅当,即时等号成立.
而,故函数的最大值为.
(2)当,时,有,所以
即,当且仅当时等号成立.因此的最小值为.
恒成立恒成立.
故实数的取值范围是.
12.采用第(1)种方案,利用旧墙米为矩形的一面边长时,建墙总费用最省,为元.
【解析】
【分析】
以建造总费用为目标函数,把方案(1)和(2)的函数关系式求出来,通过函数求最小值来解决问题
【详解】
利用旧墙的一面矩形边长为x米,则矩形的另一面边长为米,
方案(1):利用旧墙的一段x米,(x<14)为矩形一面边长,则修旧墙费用为元,将剩余旧墙拆得的材料建设新墙的费用为元,其余建新墙的费用为元,故总费用为,利用基本不等式可得:,当且仅当,即时,等号成立,即;
方案(2)若利用旧墙的一面矩形边长,则修旧墙的费用为元,建新墙的费用为元,故总费用,设,则
,因为,所以,,从而,所以函数在上为增函数,故当时,.
综上所述,采用第(1)种方案,利用旧墙12米为矩形的一面边长时,建墙总费用最省,为元.
13.(1)2;
(2)2.
【解析】
【分析】
(1)由基本不等式求得函数的最小值,即点的纵坐标的最小值;
(2)设点P的坐标,由点到直线的距离公式及基本不等式即可得解.
(1)
因为,所以,当且仅当时等号成立,
故得到函数最小值为
点的纵坐标的最小值
(2)
设点,
则点到直线的距离,
因为,所以,当且仅当时,等号成立,
所以点到直线的距离的最小值2.
14.(1)9
(2)证明见解析
【解析】
【分析】
(1)分类讨论求出f(x)的分段函数解析式,求f(x)值域即可;
(2)两边平方结合基本不等式求出最小值,展开即可求其最小值.
(1)
∵
∴当时,;
当时,;
当时,;
∴函数的最小值为9,即m=9.
(2)
由(1)知,即证,
∵,
∴,
即,
∴.
15.(1)证明见解析;(2)3.
【解析】
【分析】
(1)直接利用基本不等式即可证明;
(2)原等式化简可得,由(1)的结论,即可得到答案.
【详解】
(1)因为,由基本不等式可得,,,三式相乘可得:,当且仅当时,等号成立.
(2),
由(1)可得,当且仅当时,取最小值为3.
【点睛】
本题考查基本不等式在证明不等式成立以及求最小值中的应用,在利用基本不等式时,注意使用的前提条件,属于中档题
16.(1);(2).
【解析】
【详解】
试题分析:第一步利用正弦定理进行“边转角”化为三角函数关系,借助两角和公式进行恒等变形,求出角A的余弦值,进而求出角A;第二步利用余弦定理,转化为b+c与bc的关系,然后利用基本不等式“等转不等”,求出b+c的范围,再根据三角形两边之和大于第三边,求出范围.
试题解析:
(1)依题意由正弦定理可得:
又.
(2)由余弦定理知:
(当且仅当时成立)
,又
故的取值范围是.
【点睛】有关解斜三角形问题,常用正弦定理、余弦定理、面积公式等,多用正弦定理和余弦定理进行“边角转化”,求范围或最值问题常用方法有两种,第一边化角,利用三角函数式恒等变形转化为某个角的三角函数式,根据角的范围研究函数值的范围,另一种方法是化边,利用基本不等式求范围或最值.
17.(1)(2)(3)证明见解析;
【解析】
【分析】
(1)由题意设圆心为,半径,利用基本不等式求出半径的最小值,从而得到面积的最小值;
(2)由,知,运用两直线垂直的条件:斜率之积为,解方程可得,讨论的取值,求得圆心到直线的距离的距离,即可得到所求圆的方程;
(3)设,,,求得,的坐标,和的方程,联立圆的方程,运用韦达定理,.设,则.设直线的方程为,代入圆的方程,运用韦达定理,可得,的关系,即可得到所求定点.
【详解】
解:(1)由题意可设圆的圆心为,
则半径为(当且仅当时取等号),
所以圆的面积最小值为.
(2)由,知.
所以,解得.
当时,圆心到直线的距离小于半径,符合题意;
当时,圆心到直线的距离大于半径,不符合题意.
所以,所求圆的方程为.
(3)设,,,又知,,
所以,.
显然,设,则.
从而直线方程为:,
与圆的方程联立,
消去,可得:,
所以,,即;
同理直线方程为:,
与圆的方程联立,
消去,可得:,
所以,,即.
所以;
.
消去参数整理得. ①
设直线的方程为,代入,
整理得.
所以,.
代入①式,并整理得,
即,解得或.
当时,直线的方程为,过定点;
当时,直线的方程为,过定点
第二种情况不合题意(因为,在直径的异侧),舍去.
所以,直线过定点.
【点睛】
本题考查圆的方程的求法和运用,注意运用联立直线方程和圆的方程,消去一个未知数,运用韦达定理,考查直线方程的运用和恒过定点的求法,考查运算能力,属于难题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
