人教A版(2019)必修第一册新高考名师导学第四章4.5函数的应用(二)(Word含答案)
文档属性
| 名称 | 人教A版(2019)必修第一册新高考名师导学第四章4.5函数的应用(二)(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 981.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 17:32:00 | ||
图片预览




文档简介
人教A版(2019) 必修第一册 新高考名师导学 第四章 4.5 函数的应用(二)
一、解答题
1.利用计算器,用二分法求方程的近似解(精确度为0.1).
2.若,解关于x的不等式:.
3.某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 2014 2015 2016 2017 2018 2019
人数(单位:千人) 2082 2135 2203 2276 2339 2385
(1)根据表中的数据判断从2014年到2019年哪个跨年度的人口增长数量最大?并描述该地人口数量的变化趋势;
(2)研究人员用函数拟合该地的人口数量,其中的单位是年,2014年年初对应时刻,的单位是千人,经计算可得,请解释的实际意义.
4.如图,正方体的棱长为2,分别是和的中点.
(1)求证:平面.
(2)求M到平面的距离.
5.用二分法求函数 在区间内的一个零点(精度为0.1).
6.已知函数,.
(1)求函数单调性;
(2)求函数最大值和最小值.
7.已知函数和的定义域分别为和,若对任意,恰好存在个不同的实数,使得(其中),则称为的“重覆盖函数”.
(1)判断是否为的“重覆盖函数”,如果是,求出的值;如果不是,说明理由.
(2)若,为的“2重覆盖函数”,求实数的取值范围;
(3)函数表示不超过的最大整数,如.若为的“2021重覆盖函数”请直接写出正实数的取值范围(无需解答过程).
8.假设关于某设备的使用年限(年)和所支出的年平均维修费用(万元)(即维修费用之和除以使用年限),有如下的统计资料:
(1)求关于的线性回归方程;
(2)估计使用年限为10年时所支出的年平均维修费用是多少
参考公式:
9.计算下列各式的值:
(1)
(2).
10.分别求函数的定义域为下列区间时的最值:
(1);
(2);
(3).
11.若常数使得关于的方程有唯一解,求的取值范围.
12.已知椭圆的离心率为,点在上.
(1)求椭圆的方程;
(2)设三点均在椭圆上,为坐标原点,,证明:四边形的面积为定值.
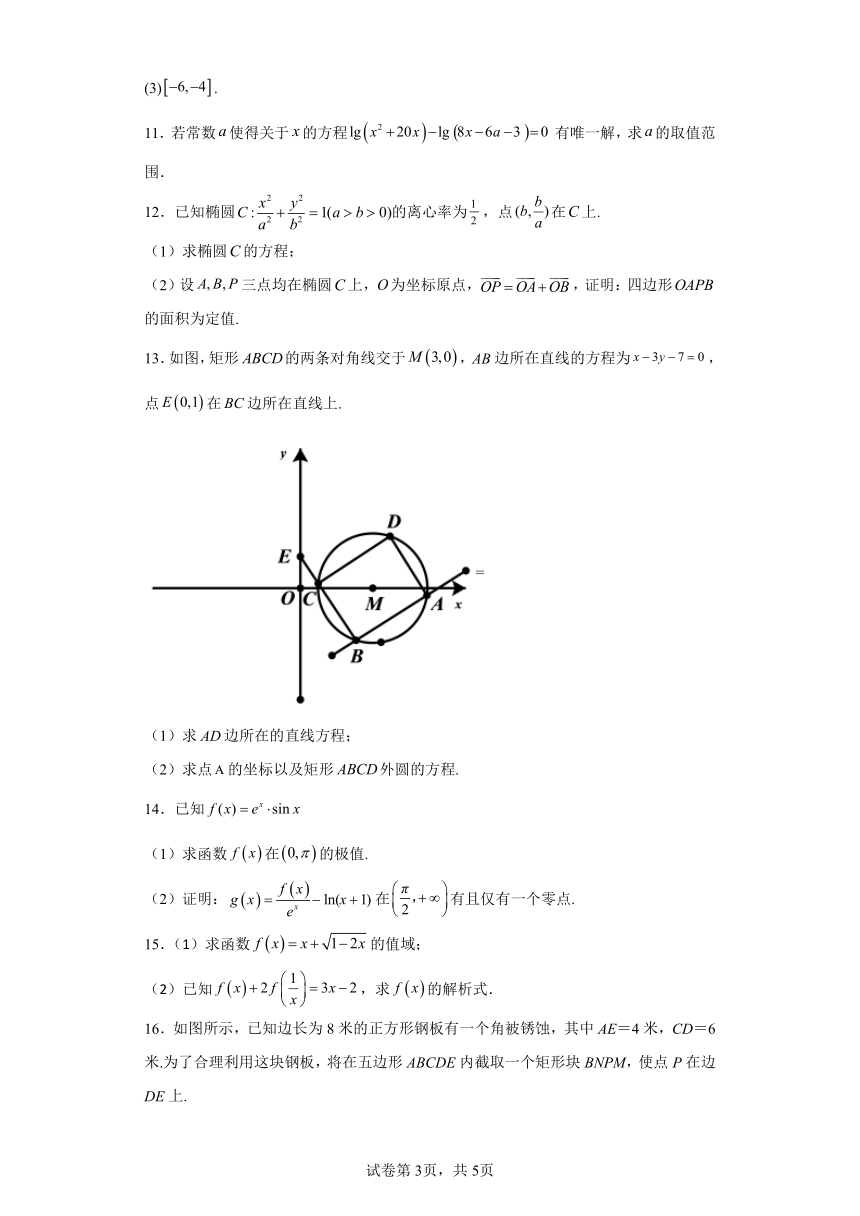
13.如图,矩形的两条对角线交于,边所在直线的方程为,点在边所在直线上.
=
(1)求边所在的直线方程;
(2)求点的坐标以及矩形外圆的方程.
14.已知
(1)求函数在的极值.
(2)证明:在有且仅有一个零点.
15.(1)求函数的值域;
(2)已知,求的解析式.
16.如图所示,已知边长为8米的正方形钢板有一个角被锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.
(1)设MP=x米,PN=y米,将y表示成x的函数,求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
17.(1)(2)(3)分别是函数和在不同范围的图象,借助计算工具估算出使的的取值范围(精确到0.01).
(1) (2) (3)
18.某大学生利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价和销售量之间的一组数据如表所示:
月份 7 8 9 10 11 12
销售单价(元) 9 9.5 10 10.5 11 8.5
销售量(元) 11 10 8 6 5 14
(1)根据7至11月份的数据,求出关于的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过2件,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多元才能获得最大利润?(注:利润=销售收入-成本).
参考数据:,.
参考公式:回归直线方程,其中,.
19.已知函数.
(1)讨论的单调性;
(2)讨论在上的零点个数.
20.求方程3x+=0的近似解(精确度0.1).
21.用二分法求方程2x3+3x-3=0的一个正实数近似解(精确度是0.1).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1..
【解析】
【分析】
根据函数的单调性以及零点存在性定理判断方程解所在区间,然后使用二分法求方程近似解的步骤依次计算,可得结果.
【详解】
令,可知函数是连续的单调递增的函数
,.
所以可知方程的在区间内
利用二分法,列表如下:
区间 中点值 中点的函数值
2.5
2.75 0.189332693
2.625 0.044129307
2.5625
∵,
故方程的近似解.
【点睛】
本题考查零点存在性定理以及利用二分法求解方程的近似解,着重对概念的掌握以及步骤的理解,属基础题.
2.详见解析
【解析】
【分析】
化分式不等式为整式不等式,然后对与,的大小关系分类讨论,利用穿针引线法即可求出不等式的解集.
【详解】
原不等式可化为,
(1)当时,原不等式的解集为;
(2)当时,原不等式的解集为;
(3)当时,原不等式的解集为.
【点睛】
本题主要考查分式不等式的解法及穿针引线法在解不等式中的应用,同时考查分类讨论的思想,属于中档题.
3.(1)2016年到2017年的人口的增长数量最大,2014年到2019年该地每年人口的增长数量呈先递增后递减的趋势(或2014年到2019年该地每年人口总数呈逐渐递增的趋势);(2)到2020年中,该地的总人数大约可增长到2450千人(或到2020年6月末或7月初,该地的总人数大约可增长到2450千人)
【解析】
(1)根据表中的数据,逐年作差,可得从2014年到2019年每年增加的数量,逐年增多,从2017后,增加的人数逐年减少;
(2)根据函数的表达式及题意,可得表示2014+t年的人口数量,不难得到的实际意义.
【详解】
(1)从2014年到2015年该地的人口增长数量:;
从2015年到2016年该地的人口增长数量:;
从2016年到2017年该地的人口增长数量:;
从2017年到2018年该地的人口增长数量:;
从2018年到2019年该地的人口增长数量:;
故2016年到2017年的人口的增长数量最大.
2014年到2019年该地每年人口的增长数量呈先递增后递减的趋势.
(或2014年到2019年该地每年人口总数呈逐渐递增的趋势).
(2)由题意,2014年年初对应时刻,表示2014+t年的人口数量,
,表示2014+6.5=2020.5年的人口数量,
故其实际意义为:到2020年中,该地的总人数大约可增长到2450千人.
或到2020年6月末或7月初,该地的总人数大约可增长到2450千人.
【点睛】
本题考查统计表及函数模型的应用,考查运算求解及数学分析能力,属于简单题.
4.(1)见解析(2)
【解析】
【分析】
(1)连接,证明四边形是平行四边形即可得出,故平面;(2)根据求出M到平面的距离.
【详解】
解:(1)证明:连接,
∵,
∴,
∴四边形是平行四边形,
∴,
又平面,平面,
∴平面.
(2)解:连接,
则,
又,
∴,∴.
∴,
设M到平面的距离为d,则,
∴.即M到平面的距离为.
【点睛】
本题考查了线面平行的判定,棱锥的体积计算,属于中档题.
5.1.3125.
【解析】
【分析】
由零点的存在定理,用二分法,逐步计算,直到区间长度小于等于0.1为止,最后所得区间内的任何一个数均可作为函数的零点.
【详解】
∵,
,
∴函数在区间内存在零点,取区间作为计算的初始区间,用二分法逐次计算,列表如下:
区间 区间中点 中点函数值(或近似值)
(1,1.5) 1.25 -0.297
(1.25,1.5) 1.375 0.225
(1.25,1.375) 1.3125 -0.052
(1.3125,1.375) 1.34375 0.083
∵,
∴函数的零点落在区间内,
故函数零点的近似值可取为1.3125.
【点睛】
本题主要考查二分法求函数的零点,熟记二分法的一般步骤即可,属于常考题型.
6.(1)函数在区间上为增函数;
(2)最大值为,最小值为.
【解析】
【分析】
(1)利用二次函数的性质可判断函数的单调性;
(2)利用函数在区间上为增函数,由此求得函数的最值.
(1)
二次函数,对称轴为y轴,开口向上,
函数在上单调递减,在上单调递增,
故函数在区间上为增函数,
(2)
由函数在区间上为增函数,
,.
因此,函数在区间上的最大值为,最小值为.
7.(1)是的“n重覆盖函数”,;
(2)
(3)
【解析】
【分析】
(1)根据,可得,得出对于任意,都能找到一个,使得,即得证;
(2)将题转化为对任意,有2个实根,根据的性质即可求解;
(3)将题转化为对于任意,要有2021个根,根据取整函数的性质列出不等式求解即可.
(1)
(1),
由定义可得,对任意,恰好存在n个不同的实数,使得(其中),
即,可得,
所以对于任意,都能找到一个,使得,
是的“n重覆盖函数”,;
(2)
(2)可得的定义域为,
即对任意,存在2个不同的实数,使得(其中),
,,
即,
即对任意,有2个实根,
当时,已有一个根,故只需时,仅有1个根,
当时,,符合题意,
当时,则需满足,解得,
当时,抛物线开口向下,,,要仅有1个根,
需满足,解得
综上,实数的取值范围是;
(3)
(3),
对于任意,要有2021个根,
,
作出函数的图像,如下图:
要使有2021个根,需,
又,解得
所以正实数的取值范围
【点睛】
关键点睛:本题考查函数新定义,解题的关键是正确理解“n重覆盖函数”的概念,将题目转化为方程根的问题,考查学生的分析转化能力,数形结合能力,属于难题.
8.(1);(2)万元
【解析】
【分析】
(1)先求出样本中心点及代入公式求得,再将代入回归直线求得的值,可得线性回归方程;(2)在(1)中求得的线性回归方程中,取x=10,求得y值得答案.
【详解】
(1)由题表数据可得,
由公式可得,
即回归方程是.
(2)由(1)可得,当时,;
即,使用年限为10年时所支出的年平均维修费用是万元.
【点睛】
本题考查线性回归方程,考查计算能力,是基础题.
9.(1);(2)
【解析】
【分析】
(1)直接利用根式与分数指数幂的运算法则求解即可,化简过程注意避免出现符号错误;(2)直接利用对数的运算法则求解即可,解答过程注意避免出现计算错误.
【详解】
(1)原式=
=
=
=
(2)原式=
=
==
【点睛】
本题主要考查函数的定义域、指数幂的运算,属于中档题. 指数幂运算的四个原则:(1)有括号的先算括号里的,无括号的先做指数运算;(2)先乘除后加减,负指数幂化成正指数幂的倒数;(3)底数是负数,先确定符号,底数是小数,先化成分数,底数是带分数的,先化成假分数;(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答(化简过程中一定要注意等价性,特别注意开偶次方根时函数的定义域)
10.(1)最小值-9,最大值91(2)最小值7,最大值27(3)最小值-8,最大值0
【解析】
由二次函数性质可确定函数在所给区间内的单调性,结合单调性确定最值点,代入即可求得所求最值.
【详解】
是开口方向向上,对称轴为的二次函数
在上单调递减,在上单调递增
(1)当时,在上单调递减,在上单调递增
,
(2)当时,单调递增
,
(3)当时,单调递减
,
【点睛】
本题考查二次函数最值的求解问题,关键是明确二次函数最值的求解必须关注对称轴的位置;当对称轴位于所给区间内时,则函数在对称轴处必取得一个最值,另一个最值在离轴较远的区间端点处;当对称轴不位于所给区间内时,则函数为单调函数.
11.
【解析】
【分析】
根据已知条件可得出关于、的等式,可得出在时有唯一解,数形结合可得出结果.
【详解】
由,解得或.
由已知可得,可得,
所以,在时有唯一解 ,
作出函数在的图象如下图所示:
因为,,
由图可知,当时,直线与函数在上的图象有且只有一个交点,
因此,实数的取值范围是.
12.(1);(2)证明见解析.
【解析】
【详解】
试题分析:(1)由题意,得.(2)由题意,设,,,, ,,.
试题解析:
(1)由已知可得,,,联立解得,,,
∴椭圆的方程为.
(2)当轴时,方程为,此时.
当与轴不垂直时,设,,.
将代入方程整理得,,,
,∴ ,
将代入方程整理得,∴,,
,
原点到直线的距离,∴.
∴四边形的面积为定值3.
点睛:本题考查直线和椭圆的位置关系.联立直线和椭圆方程,得到韦达定理,,由向量可知,,代入椭圆方程得,由,分别求出和,得到面积为定值3.
13.(1);(2),外接圆的标准方程为..
【解析】
(1)先求出直线的方程为 ,设直线的方程为,利用到直线的距离与到直线的距离相等可求的值.
(2)利用(1)求出的的直线方程和直线的方程联立,可求的坐标,求出半径的长度后可求圆的标准方程.
【详解】
设直线的方程为:,因直线过点,
故即,故的直线方程为:.
设直线的方程为:,因为为矩形对角线的交点,
故,故(舍)或.
所以的方程为:.
(2)由得,故,
所以,
故外接圆的标准方程为:.
【点睛】
本题考查直线方程、圆的方程,注意求直线方程时可依据平行或垂直作合理假设,如果已知直线,则与平行的直线可设为,与垂直的直线可设为.求圆的方程时,要注意利用圆的几何性质,如:(1)圆心与圆上的一点的连线的长为半径;(2)圆心在弦的中垂线上;(3)圆心在过切线且垂直于切线的直线上;(4)圆关于直径成轴对称图形.
14.(1),无极小值;(2)见解析
【解析】
【分析】
(1)对函数求导,并求出该函数的极值点,分析函数在极值点左右两边的单调性,确定极值的属性,然后将极值点代入函数的解析式可得出答案;
(2)首先考查,利用导数研究函数在该区间上的单调性,并确定和的正负,结合零点存在定理来得出函数的零点个数;
其次考查,利用放缩法得出可知函数在该区间上不存在零点.
结合上述两个步骤证明结论.
【详解】
(1),
令,得,又,故.
令,得;令,得.
所以,函数在上单调递增,在上单调递减,
故;无极小值.
(2)当时,,,于是,
此时,函数单调递减,
,
,
由函数零点存在性定理知,函数在上有且只有一个零点.
当上,.
综上所述,函数有且只有个零点.
【点睛】
本题考查函数的极值与导数、函数的零点个数问题,一般而言,对于不带参数的函数零点个数问题,要利用导数研究函数的单调性,并结合零点存在定理确定零点个数,是解决函数零点个数的常用方法,考查推理论证能力以及分析问题的能力,属于难题.
15.(1);(2)
【解析】
【分析】
(1)由题意设,求出的范围和的表达式,代入化简后,根据一元二次函数的性质和的范围,求出函数的值域;
(2)令代换代入原方程化简,与原方程联立后求出的解析式.
【详解】
(1)设,则,,
代入得,
,
图像为开口向下,对称轴为的抛物线
因为,所以函数的最大值是1,即函数的值域是;
(2)由题意得,,①
令代换,代入得,,②
由①②联立方程组,解得.
【点睛】
本题考查了换元法求函数的值域和列方程组求函数的解析式等问题,以及一元二次函数求最值的方法,属于中档题.
16.(1);(2)48.
【解析】
【分析】
(1)利用三角形相似,可得函数得解析式与定义域;
(2)表示出面积,结合二次函数得性质即可求出最大值.
【详解】
解 (1)如图所示,延长NP交AF于点Q,
所以PQ=8-y,EQ=x-4.
在中, ,所以.
所以,定义域为.
(2)设矩形BNPM的面积为S,
则,开口向下,且对称轴为,则在上单调递增,所以当x=8时,S取最大值48,所以矩形BNPM面积的最大值为48.
17.
【解析】
从图象可以看出,有两个解,一个在上,一个在上,可用二分法求解.
【详解】
记,计算,,,
,,,,,近似解取,
,,,,,近似解取,
故估算范围是
【点睛】
本题考查指数函数的图象,考查二分法求近似解.属于基础题.
18.(1);(2)可以认为所得的回归直线方程是理想的;(3)该产品的销售单价为7.5元/件时,获得的利润最大.
【解析】
(1)计算、,求出回归系数,写出回归直线方程;
(2)根据回归直线方程,计算对应的数值,判断回归直线方程是否理想;
(3)求销售利润函数,根据二次函数的图象与性质求最大值即可.
【详解】
(1)因为,,所以,则,
∴关于的回归直线方程为
(2)剩余数据为12月份,此时,,现进行检测,当时,
,则,所以可以认为所得的回归直线方程是理想的.
(3)令销售利润为,则
.
∴当时,取最大值.
所以该产品的销售单价为7.5元/件时,获得的利润最大.
【点睛】
函数关系是一种确定的关系,相关关系是一种非确定的关系.事实上,函数关系是两个非随机变量的关系,而相关关系是非随机变量与随机变量的关系,如果线性相关,则直接根据用公式求,写出回归方程,回归直线方程恒过点.
19.(1)见解析;(2)见解析
【解析】
【分析】
(1)先确定单调性,然后求导数,再通过讨论的范围,确定的符号,从而确定单调性.
(2)根据的单调性,分别讨论当时,在上的单调性,从而确定在区间两端点的函数值符号以及最值的符号,结合零点存在性定理,即可判断在上的零点个数情况.
【详解】
解:(1)函数的定义域为..
当时,即,,在上单调递增,
∴在上单调递增.
当时,即,当时,,当时,,
∴在上单调递减,在上单调递增.
∴当时,在上单调递增.
当时,在上单调递减,在上单调递增.
(2)设,则由(1)知
①当时,即,当时,,在单调递减
,
∴当,即,时,在上恒成立,
∴当时,在内无零点.
当,即,时,,
根据零点存在性定理知,此时,在内有零点,
∵在内单调递减,∴此时,在有一个零点.
②当时,即,当时,,在单调递增,
,.
∴当,即时,,根据零点存在性定理,此时,在内有零点.
∵在内单调递增,∴此时,在有一个零点.
当时,,∴此时,在无零点.
③当时,即,当时,;当时,;
则在单调递减,在单调递增.
∴在上恒成立,∴此时,在内无零点.
∴综上所述:
当时,在内有1个零点;
当时,在有一个零点;
当时,在无零点.
【点睛】
本题主要考查了函数单调性的判断以及零点个数问题,属于难题.函数单调性问题主要运用导数法进行讨论.而判断函数零点个数的方法有:
(1)解方程法:若对应方程可解时,通过解方程,则有几个解就有几个零点.
(2)零点存在性定理法:利用定理不仅要判断函数在区间上是连续不断的曲线,且,还必须结合函数的图像与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点.
(3)数形结合法:转化为两个函数的图像交点个数问题,先画出两个函数的图像,再看其交点的个数,其中交点个数就是函数零点的个数.
20.0.4385.
【解析】
【分析】
根据指数函数的图象,求得方程解存在的区间以及解的个数,再利用二分法,结合精确度即可求得结果.
【详解】
原方程可化为3x+1=0,即3x=1.
令g(x)=3x,h(x)=1,
在同一平面直角坐标系中,分别画出函数g(x)=3x与h(x)=1的简图.
g(x)与h(x)图象的交点的横坐标位于区间(1,0),且只有一交点,
故原方程只有一个解x=x0.
令f(x)=3x+=3x+1,
因为f(0)=11+1=1>0,
f(0.5)=2+1=<0,
故x0∈(-0.5,0).
用二分法求解列表如下:
中点值 中点(端点)函数值及符号 选取区间
f(-0.5)<0,f(0)>0 (-0.5,0)
-0.25 f(-0.25)≈0.426 5>0 (-0.5,-0.25)
-0.375 f(-0.375)≈0.062 3>0 (-0.5,-0.375)
-0.437 5 f(-0.437 5)≈-0.159 3<0 (-0.437 5,-0.375)
因为|-0.437 5-(-0.375)|=0.062 5<0.1,
故原方程的近似解可取区间(-0.437 5,-0.375)中的任意一个数,
本题中不妨取0.4385.
【点睛】
本题考查利用二分法求方程的近似根,注意精确度的限制即可,属基础题.
21.0.687 5
【解析】
【分析】
根据题意,设函数,分析可得(1),函数在区间上有零点,由二分法依次分析即可得答案.
【详解】
解:令f(x)=2x3+3x-3,经计算,
f(0)=-3<0,f(1)=2>0,f(0)·f(1)<0,
所以函数f(x)在(0,1)内存在零点,
即方程2x3+3x-3=0在(0,1)内有解.
取(0,1)的中点0.5,经计算f(0.5)<0,
又f(1)>0,所以方程2x3+3x-3=0在(0.5,1)内有解.
如此继续下去,得到方程的正实数解所在的区间,如下表:
(a,b) 中点c f(a) f(b)
(0,1) 0.5 f(0)<0 f(1)>0 f(0.5)<0
(0.5,1) 0.75 f(0.5)<0 f(1)>0 f(0.75)>0
(0.5,0.75) 0.625 f(0.5)<0 f(0.75)>0 f(0.625)<0
(0.625,0.75) 0.6875 f(0.625)<0 f(0.75)>0 f(0.6875)<0
由于|0.6875-0.75|=0.0625<0.1,
所以方程2x3+3x-3=0的一个精确度为0.1的正实数近似解可取为0.687
答案第1页,共2页
答案第1页,共2页
一、解答题
1.利用计算器,用二分法求方程的近似解(精确度为0.1).
2.若,解关于x的不等式:.
3.某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 2014 2015 2016 2017 2018 2019
人数(单位:千人) 2082 2135 2203 2276 2339 2385
(1)根据表中的数据判断从2014年到2019年哪个跨年度的人口增长数量最大?并描述该地人口数量的变化趋势;
(2)研究人员用函数拟合该地的人口数量,其中的单位是年,2014年年初对应时刻,的单位是千人,经计算可得,请解释的实际意义.
4.如图,正方体的棱长为2,分别是和的中点.
(1)求证:平面.
(2)求M到平面的距离.
5.用二分法求函数 在区间内的一个零点(精度为0.1).
6.已知函数,.
(1)求函数单调性;
(2)求函数最大值和最小值.
7.已知函数和的定义域分别为和,若对任意,恰好存在个不同的实数,使得(其中),则称为的“重覆盖函数”.
(1)判断是否为的“重覆盖函数”,如果是,求出的值;如果不是,说明理由.
(2)若,为的“2重覆盖函数”,求实数的取值范围;
(3)函数表示不超过的最大整数,如.若为的“2021重覆盖函数”请直接写出正实数的取值范围(无需解答过程).
8.假设关于某设备的使用年限(年)和所支出的年平均维修费用(万元)(即维修费用之和除以使用年限),有如下的统计资料:
(1)求关于的线性回归方程;
(2)估计使用年限为10年时所支出的年平均维修费用是多少
参考公式:
9.计算下列各式的值:
(1)
(2).
10.分别求函数的定义域为下列区间时的最值:
(1);
(2);
(3).
11.若常数使得关于的方程有唯一解,求的取值范围.
12.已知椭圆的离心率为,点在上.
(1)求椭圆的方程;
(2)设三点均在椭圆上,为坐标原点,,证明:四边形的面积为定值.
13.如图,矩形的两条对角线交于,边所在直线的方程为,点在边所在直线上.
=
(1)求边所在的直线方程;
(2)求点的坐标以及矩形外圆的方程.
14.已知
(1)求函数在的极值.
(2)证明:在有且仅有一个零点.
15.(1)求函数的值域;
(2)已知,求的解析式.
16.如图所示,已知边长为8米的正方形钢板有一个角被锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.
(1)设MP=x米,PN=y米,将y表示成x的函数,求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
17.(1)(2)(3)分别是函数和在不同范围的图象,借助计算工具估算出使的的取值范围(精确到0.01).
(1) (2) (3)
18.某大学生利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价和销售量之间的一组数据如表所示:
月份 7 8 9 10 11 12
销售单价(元) 9 9.5 10 10.5 11 8.5
销售量(元) 11 10 8 6 5 14
(1)根据7至11月份的数据,求出关于的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过2件,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多元才能获得最大利润?(注:利润=销售收入-成本).
参考数据:,.
参考公式:回归直线方程,其中,.
19.已知函数.
(1)讨论的单调性;
(2)讨论在上的零点个数.
20.求方程3x+=0的近似解(精确度0.1).
21.用二分法求方程2x3+3x-3=0的一个正实数近似解(精确度是0.1).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1..
【解析】
【分析】
根据函数的单调性以及零点存在性定理判断方程解所在区间,然后使用二分法求方程近似解的步骤依次计算,可得结果.
【详解】
令,可知函数是连续的单调递增的函数
,.
所以可知方程的在区间内
利用二分法,列表如下:
区间 中点值 中点的函数值
2.5
2.75 0.189332693
2.625 0.044129307
2.5625
∵,
故方程的近似解.
【点睛】
本题考查零点存在性定理以及利用二分法求解方程的近似解,着重对概念的掌握以及步骤的理解,属基础题.
2.详见解析
【解析】
【分析】
化分式不等式为整式不等式,然后对与,的大小关系分类讨论,利用穿针引线法即可求出不等式的解集.
【详解】
原不等式可化为,
(1)当时,原不等式的解集为;
(2)当时,原不等式的解集为;
(3)当时,原不等式的解集为.
【点睛】
本题主要考查分式不等式的解法及穿针引线法在解不等式中的应用,同时考查分类讨论的思想,属于中档题.
3.(1)2016年到2017年的人口的增长数量最大,2014年到2019年该地每年人口的增长数量呈先递增后递减的趋势(或2014年到2019年该地每年人口总数呈逐渐递增的趋势);(2)到2020年中,该地的总人数大约可增长到2450千人(或到2020年6月末或7月初,该地的总人数大约可增长到2450千人)
【解析】
(1)根据表中的数据,逐年作差,可得从2014年到2019年每年增加的数量,逐年增多,从2017后,增加的人数逐年减少;
(2)根据函数的表达式及题意,可得表示2014+t年的人口数量,不难得到的实际意义.
【详解】
(1)从2014年到2015年该地的人口增长数量:;
从2015年到2016年该地的人口增长数量:;
从2016年到2017年该地的人口增长数量:;
从2017年到2018年该地的人口增长数量:;
从2018年到2019年该地的人口增长数量:;
故2016年到2017年的人口的增长数量最大.
2014年到2019年该地每年人口的增长数量呈先递增后递减的趋势.
(或2014年到2019年该地每年人口总数呈逐渐递增的趋势).
(2)由题意,2014年年初对应时刻,表示2014+t年的人口数量,
,表示2014+6.5=2020.5年的人口数量,
故其实际意义为:到2020年中,该地的总人数大约可增长到2450千人.
或到2020年6月末或7月初,该地的总人数大约可增长到2450千人.
【点睛】
本题考查统计表及函数模型的应用,考查运算求解及数学分析能力,属于简单题.
4.(1)见解析(2)
【解析】
【分析】
(1)连接,证明四边形是平行四边形即可得出,故平面;(2)根据求出M到平面的距离.
【详解】
解:(1)证明:连接,
∵,
∴,
∴四边形是平行四边形,
∴,
又平面,平面,
∴平面.
(2)解:连接,
则,
又,
∴,∴.
∴,
设M到平面的距离为d,则,
∴.即M到平面的距离为.
【点睛】
本题考查了线面平行的判定,棱锥的体积计算,属于中档题.
5.1.3125.
【解析】
【分析】
由零点的存在定理,用二分法,逐步计算,直到区间长度小于等于0.1为止,最后所得区间内的任何一个数均可作为函数的零点.
【详解】
∵,
,
∴函数在区间内存在零点,取区间作为计算的初始区间,用二分法逐次计算,列表如下:
区间 区间中点 中点函数值(或近似值)
(1,1.5) 1.25 -0.297
(1.25,1.5) 1.375 0.225
(1.25,1.375) 1.3125 -0.052
(1.3125,1.375) 1.34375 0.083
∵,
∴函数的零点落在区间内,
故函数零点的近似值可取为1.3125.
【点睛】
本题主要考查二分法求函数的零点,熟记二分法的一般步骤即可,属于常考题型.
6.(1)函数在区间上为增函数;
(2)最大值为,最小值为.
【解析】
【分析】
(1)利用二次函数的性质可判断函数的单调性;
(2)利用函数在区间上为增函数,由此求得函数的最值.
(1)
二次函数,对称轴为y轴,开口向上,
函数在上单调递减,在上单调递增,
故函数在区间上为增函数,
(2)
由函数在区间上为增函数,
,.
因此,函数在区间上的最大值为,最小值为.
7.(1)是的“n重覆盖函数”,;
(2)
(3)
【解析】
【分析】
(1)根据,可得,得出对于任意,都能找到一个,使得,即得证;
(2)将题转化为对任意,有2个实根,根据的性质即可求解;
(3)将题转化为对于任意,要有2021个根,根据取整函数的性质列出不等式求解即可.
(1)
(1),
由定义可得,对任意,恰好存在n个不同的实数,使得(其中),
即,可得,
所以对于任意,都能找到一个,使得,
是的“n重覆盖函数”,;
(2)
(2)可得的定义域为,
即对任意,存在2个不同的实数,使得(其中),
,,
即,
即对任意,有2个实根,
当时,已有一个根,故只需时,仅有1个根,
当时,,符合题意,
当时,则需满足,解得,
当时,抛物线开口向下,,,要仅有1个根,
需满足,解得
综上,实数的取值范围是;
(3)
(3),
对于任意,要有2021个根,
,
作出函数的图像,如下图:
要使有2021个根,需,
又,解得
所以正实数的取值范围
【点睛】
关键点睛:本题考查函数新定义,解题的关键是正确理解“n重覆盖函数”的概念,将题目转化为方程根的问题,考查学生的分析转化能力,数形结合能力,属于难题.
8.(1);(2)万元
【解析】
【分析】
(1)先求出样本中心点及代入公式求得,再将代入回归直线求得的值,可得线性回归方程;(2)在(1)中求得的线性回归方程中,取x=10,求得y值得答案.
【详解】
(1)由题表数据可得,
由公式可得,
即回归方程是.
(2)由(1)可得,当时,;
即,使用年限为10年时所支出的年平均维修费用是万元.
【点睛】
本题考查线性回归方程,考查计算能力,是基础题.
9.(1);(2)
【解析】
【分析】
(1)直接利用根式与分数指数幂的运算法则求解即可,化简过程注意避免出现符号错误;(2)直接利用对数的运算法则求解即可,解答过程注意避免出现计算错误.
【详解】
(1)原式=
=
=
=
(2)原式=
=
==
【点睛】
本题主要考查函数的定义域、指数幂的运算,属于中档题. 指数幂运算的四个原则:(1)有括号的先算括号里的,无括号的先做指数运算;(2)先乘除后加减,负指数幂化成正指数幂的倒数;(3)底数是负数,先确定符号,底数是小数,先化成分数,底数是带分数的,先化成假分数;(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答(化简过程中一定要注意等价性,特别注意开偶次方根时函数的定义域)
10.(1)最小值-9,最大值91(2)最小值7,最大值27(3)最小值-8,最大值0
【解析】
由二次函数性质可确定函数在所给区间内的单调性,结合单调性确定最值点,代入即可求得所求最值.
【详解】
是开口方向向上,对称轴为的二次函数
在上单调递减,在上单调递增
(1)当时,在上单调递减,在上单调递增
,
(2)当时,单调递增
,
(3)当时,单调递减
,
【点睛】
本题考查二次函数最值的求解问题,关键是明确二次函数最值的求解必须关注对称轴的位置;当对称轴位于所给区间内时,则函数在对称轴处必取得一个最值,另一个最值在离轴较远的区间端点处;当对称轴不位于所给区间内时,则函数为单调函数.
11.
【解析】
【分析】
根据已知条件可得出关于、的等式,可得出在时有唯一解,数形结合可得出结果.
【详解】
由,解得或.
由已知可得,可得,
所以,在时有唯一解 ,
作出函数在的图象如下图所示:
因为,,
由图可知,当时,直线与函数在上的图象有且只有一个交点,
因此,实数的取值范围是.
12.(1);(2)证明见解析.
【解析】
【详解】
试题分析:(1)由题意,得.(2)由题意,设,,,, ,,.
试题解析:
(1)由已知可得,,,联立解得,,,
∴椭圆的方程为.
(2)当轴时,方程为,此时.
当与轴不垂直时,设,,.
将代入方程整理得,,,
,∴ ,
将代入方程整理得,∴,,
,
原点到直线的距离,∴.
∴四边形的面积为定值3.
点睛:本题考查直线和椭圆的位置关系.联立直线和椭圆方程,得到韦达定理,,由向量可知,,代入椭圆方程得,由,分别求出和,得到面积为定值3.
13.(1);(2),外接圆的标准方程为..
【解析】
(1)先求出直线的方程为 ,设直线的方程为,利用到直线的距离与到直线的距离相等可求的值.
(2)利用(1)求出的的直线方程和直线的方程联立,可求的坐标,求出半径的长度后可求圆的标准方程.
【详解】
设直线的方程为:,因直线过点,
故即,故的直线方程为:.
设直线的方程为:,因为为矩形对角线的交点,
故,故(舍)或.
所以的方程为:.
(2)由得,故,
所以,
故外接圆的标准方程为:.
【点睛】
本题考查直线方程、圆的方程,注意求直线方程时可依据平行或垂直作合理假设,如果已知直线,则与平行的直线可设为,与垂直的直线可设为.求圆的方程时,要注意利用圆的几何性质,如:(1)圆心与圆上的一点的连线的长为半径;(2)圆心在弦的中垂线上;(3)圆心在过切线且垂直于切线的直线上;(4)圆关于直径成轴对称图形.
14.(1),无极小值;(2)见解析
【解析】
【分析】
(1)对函数求导,并求出该函数的极值点,分析函数在极值点左右两边的单调性,确定极值的属性,然后将极值点代入函数的解析式可得出答案;
(2)首先考查,利用导数研究函数在该区间上的单调性,并确定和的正负,结合零点存在定理来得出函数的零点个数;
其次考查,利用放缩法得出可知函数在该区间上不存在零点.
结合上述两个步骤证明结论.
【详解】
(1),
令,得,又,故.
令,得;令,得.
所以,函数在上单调递增,在上单调递减,
故;无极小值.
(2)当时,,,于是,
此时,函数单调递减,
,
,
由函数零点存在性定理知,函数在上有且只有一个零点.
当上,.
综上所述,函数有且只有个零点.
【点睛】
本题考查函数的极值与导数、函数的零点个数问题,一般而言,对于不带参数的函数零点个数问题,要利用导数研究函数的单调性,并结合零点存在定理确定零点个数,是解决函数零点个数的常用方法,考查推理论证能力以及分析问题的能力,属于难题.
15.(1);(2)
【解析】
【分析】
(1)由题意设,求出的范围和的表达式,代入化简后,根据一元二次函数的性质和的范围,求出函数的值域;
(2)令代换代入原方程化简,与原方程联立后求出的解析式.
【详解】
(1)设,则,,
代入得,
,
图像为开口向下,对称轴为的抛物线
因为,所以函数的最大值是1,即函数的值域是;
(2)由题意得,,①
令代换,代入得,,②
由①②联立方程组,解得.
【点睛】
本题考查了换元法求函数的值域和列方程组求函数的解析式等问题,以及一元二次函数求最值的方法,属于中档题.
16.(1);(2)48.
【解析】
【分析】
(1)利用三角形相似,可得函数得解析式与定义域;
(2)表示出面积,结合二次函数得性质即可求出最大值.
【详解】
解 (1)如图所示,延长NP交AF于点Q,
所以PQ=8-y,EQ=x-4.
在中, ,所以.
所以,定义域为.
(2)设矩形BNPM的面积为S,
则,开口向下,且对称轴为,则在上单调递增,所以当x=8时,S取最大值48,所以矩形BNPM面积的最大值为48.
17.
【解析】
从图象可以看出,有两个解,一个在上,一个在上,可用二分法求解.
【详解】
记,计算,,,
,,,,,近似解取,
,,,,,近似解取,
故估算范围是
【点睛】
本题考查指数函数的图象,考查二分法求近似解.属于基础题.
18.(1);(2)可以认为所得的回归直线方程是理想的;(3)该产品的销售单价为7.5元/件时,获得的利润最大.
【解析】
(1)计算、,求出回归系数,写出回归直线方程;
(2)根据回归直线方程,计算对应的数值,判断回归直线方程是否理想;
(3)求销售利润函数,根据二次函数的图象与性质求最大值即可.
【详解】
(1)因为,,所以,则,
∴关于的回归直线方程为
(2)剩余数据为12月份,此时,,现进行检测,当时,
,则,所以可以认为所得的回归直线方程是理想的.
(3)令销售利润为,则
.
∴当时,取最大值.
所以该产品的销售单价为7.5元/件时,获得的利润最大.
【点睛】
函数关系是一种确定的关系,相关关系是一种非确定的关系.事实上,函数关系是两个非随机变量的关系,而相关关系是非随机变量与随机变量的关系,如果线性相关,则直接根据用公式求,写出回归方程,回归直线方程恒过点.
19.(1)见解析;(2)见解析
【解析】
【分析】
(1)先确定单调性,然后求导数,再通过讨论的范围,确定的符号,从而确定单调性.
(2)根据的单调性,分别讨论当时,在上的单调性,从而确定在区间两端点的函数值符号以及最值的符号,结合零点存在性定理,即可判断在上的零点个数情况.
【详解】
解:(1)函数的定义域为..
当时,即,,在上单调递增,
∴在上单调递增.
当时,即,当时,,当时,,
∴在上单调递减,在上单调递增.
∴当时,在上单调递增.
当时,在上单调递减,在上单调递增.
(2)设,则由(1)知
①当时,即,当时,,在单调递减
,
∴当,即,时,在上恒成立,
∴当时,在内无零点.
当,即,时,,
根据零点存在性定理知,此时,在内有零点,
∵在内单调递减,∴此时,在有一个零点.
②当时,即,当时,,在单调递增,
,.
∴当,即时,,根据零点存在性定理,此时,在内有零点.
∵在内单调递增,∴此时,在有一个零点.
当时,,∴此时,在无零点.
③当时,即,当时,;当时,;
则在单调递减,在单调递增.
∴在上恒成立,∴此时,在内无零点.
∴综上所述:
当时,在内有1个零点;
当时,在有一个零点;
当时,在无零点.
【点睛】
本题主要考查了函数单调性的判断以及零点个数问题,属于难题.函数单调性问题主要运用导数法进行讨论.而判断函数零点个数的方法有:
(1)解方程法:若对应方程可解时,通过解方程,则有几个解就有几个零点.
(2)零点存在性定理法:利用定理不仅要判断函数在区间上是连续不断的曲线,且,还必须结合函数的图像与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点.
(3)数形结合法:转化为两个函数的图像交点个数问题,先画出两个函数的图像,再看其交点的个数,其中交点个数就是函数零点的个数.
20.0.4385.
【解析】
【分析】
根据指数函数的图象,求得方程解存在的区间以及解的个数,再利用二分法,结合精确度即可求得结果.
【详解】
原方程可化为3x+1=0,即3x=1.
令g(x)=3x,h(x)=1,
在同一平面直角坐标系中,分别画出函数g(x)=3x与h(x)=1的简图.
g(x)与h(x)图象的交点的横坐标位于区间(1,0),且只有一交点,
故原方程只有一个解x=x0.
令f(x)=3x+=3x+1,
因为f(0)=11+1=1>0,
f(0.5)=2+1=<0,
故x0∈(-0.5,0).
用二分法求解列表如下:
中点值 中点(端点)函数值及符号 选取区间
f(-0.5)<0,f(0)>0 (-0.5,0)
-0.25 f(-0.25)≈0.426 5>0 (-0.5,-0.25)
-0.375 f(-0.375)≈0.062 3>0 (-0.5,-0.375)
-0.437 5 f(-0.437 5)≈-0.159 3<0 (-0.437 5,-0.375)
因为|-0.437 5-(-0.375)|=0.062 5<0.1,
故原方程的近似解可取区间(-0.437 5,-0.375)中的任意一个数,
本题中不妨取0.4385.
【点睛】
本题考查利用二分法求方程的近似根,注意精确度的限制即可,属基础题.
21.0.687 5
【解析】
【分析】
根据题意,设函数,分析可得(1),函数在区间上有零点,由二分法依次分析即可得答案.
【详解】
解:令f(x)=2x3+3x-3,经计算,
f(0)=-3<0,f(1)=2>0,f(0)·f(1)<0,
所以函数f(x)在(0,1)内存在零点,
即方程2x3+3x-3=0在(0,1)内有解.
取(0,1)的中点0.5,经计算f(0.5)<0,
又f(1)>0,所以方程2x3+3x-3=0在(0.5,1)内有解.
如此继续下去,得到方程的正实数解所在的区间,如下表:
(a,b) 中点c f(a) f(b)
(0,1) 0.5 f(0)<0 f(1)>0 f(0.5)<0
(0.5,1) 0.75 f(0.5)<0 f(1)>0 f(0.75)>0
(0.5,0.75) 0.625 f(0.5)<0 f(0.75)>0 f(0.625)<0
(0.625,0.75) 0.6875 f(0.625)<0 f(0.75)>0 f(0.6875)<0
由于|0.6875-0.75|=0.0625<0.1,
所以方程2x3+3x-3=0的一个精确度为0.1的正实数近似解可取为0.687
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
