2021-2022学年北师大版九年级数学下册3.2圆的对称性 同步练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性 同步练习题 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 265.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3-2圆的对称性》同步练习题(附答案)
1.如图所示的齿轮有16个齿,每两齿之间间隔相等,相邻两止间的圆心角α的度数为( )
A.20° B.22.5° C.25° D.30°
2.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙O的直径为15,则AC长为( )
A.10 B.13 C.12 D.11
3.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连结AB,AD,若AD=1,则R的值为( )
A. B. C.1 D.
4.将一个半径为1的圆形轮子沿直线l水平向右滚动,图中显示的是轮子上的点P的起始位置与终止位置,其中在起始位置时PO∥l,在终止位置时PO与l所夹锐角为60°,则滚动前后,圆心之间的距离可能为( )
A. B. C.π D.
5.如图,半径为5的⊙O中,有两条互相垂直的弦AB、CD,垂足为点E,且AB=CD=8,则OE的长为( )
A.3 B. C.2 D.3
6.在半径为1的⊙O中,若弦AB的长为1,则弦AB所对的圆心角的度数为( )
A.90° B.60° C.30° D.15°
7.如图,MN是⊙O的直径,点A是半圆上一个三等分点,点B是的中点,点B'是点B关于MN的对称点,⊙O的半径为1,则AB'的长等于( )
A.1 B. C. D.2
8.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④+=+,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
9.在⊙O中,如果=2.那么弦AB与弦CD之间的关系是( )
A.AB=2CD B.AB>2CD C.AB<2CD D.无法确定
10.如图,在⊙O中,AC=AB,直径BC=2,,则AD= .
11.在⊙O中,弧AB的度数为50°,则弧AB所对的圆心角的度数为 .
12.如图,在⊙O中,AC=BD,∠1=30°,则∠2的度数为 .
13.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=14°,则弧AC的度数为 °.
14.如图,⊙O的弦AC=BD,且AC⊥BD于E,连接AD,若AD=3,则⊙O的周长为 .
15.已知四边形ABCD内接于⊙O,OA=5,AB=BC,E为CD上一点,且BE=BC,∠ABE=90°,则AD的长为 .
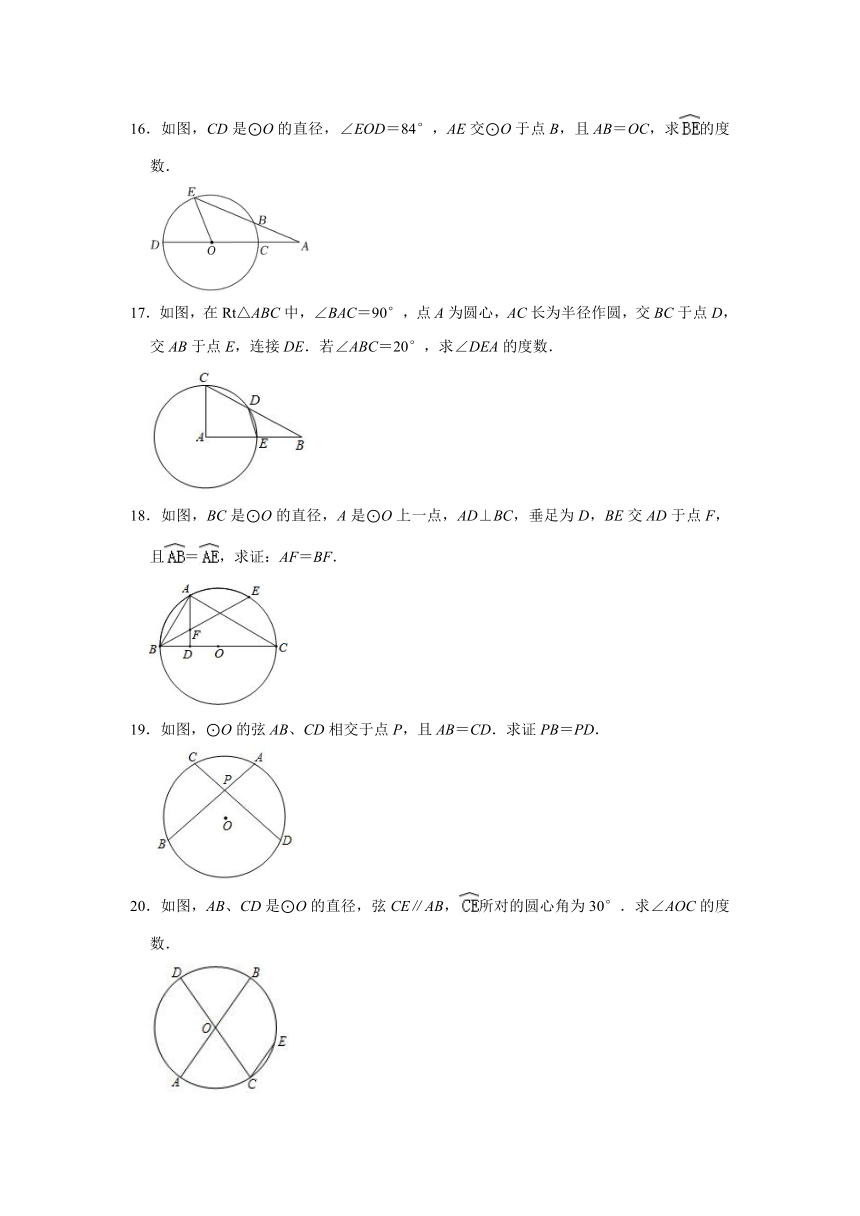
16.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,求的度数.
17.如图,在Rt△ABC中,∠BAC=90°,点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.若∠ABC=20°,求∠DEA的度数.
18.如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,BE交AD于点F,且=,求证:AF=BF.
19.如图,⊙O的弦AB、CD相交于点P,且AB=CD.求证PB=PD.
20.如图,AB、CD是⊙O的直径,弦CE∥AB,所对的圆心角为30°.求∠AOC的度数.
参考答案
1.解:由题意这是正十六边形,中心角α==22.5°,
故选:B.
2.解:连接OF,
∵DE⊥AB,AB过圆心O,
∴DE=EF,=,
∵D为弧AC的中点,
∴=,
∴=,
∴AC=DF,
∵⊙O的直径为15,
∴OF=OA=,
∵AE=3,
∴OE=OA﹣AE=,
在Rt△OEF中,由勾股定理得:EF===6,
∴DE=EF=6,
∴AC=DF=DE+EF=6+6=12,
故选:C.
3.解:∵弦AC=BD,
∴=,
∴=,
∴∠ABD=∠BAC,
∴AE=BE;
如图,连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=1,
∴R=,
故选:B.
4.解:由题意可得,圆形轮子可能滚动不止一周,设OP滚动了n周后又滚动120°后到达终止位置,
∴OP滚动的角度α=120°+360n,n为整数,
可得圆心运动前后的距离即为OP滚动完毕扫过的角度所对应的弧长,
即为2πr×=,n为整数.
当n=0时为.
故选:B.
5.解:如图,作OM⊥AB于M,ON⊥CD于N,连接OA,OC.
∴AM=BM=4,CN=DN=4,
∵OA=OC=5,
∴OM===3,ON===3,
∴OM=ON,
∵AB⊥CD,
∴∠OME=∠ONE=∠MEN=90°,
∴四边形OMEN是矩形,
∵OM=ON,
∴四边形OMEN是正方形,
∴OE=OM=3,
故选:D.
6.解:∵在半径为1的⊙O中,弦AB的长为1,
∴OA=OB=AB=1,
∴△OAB为等边三角形,
∴弦AB所对的圆心角的度数为60°.
故选:B.
7.解:连接OB、OB′,
∵点A是半圆上一个三等分点,
∴∠AON=60°,
∵点B是的中点,
∴∠BON=30°,
∵点B'是点B关于MN的对称点,
∴∠B′ON=30°,
∴∠AOB′=90°,
∴AB′==,
故选:B.
8.解:∵F为的中点,
∴=,故①正确,
∴∠FCM=∠FAC,
∵∠ACF=∠ACM+∠MCF,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴=,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴的度数+的度数=180°,
∴的度数+的度数=180°,
∴+=+=+=+,故④正确,
故选:C.
9.解:取的中点E,连接AE,BE,
则=,
∵=2,
∴==,
∴CD=AE=BE,
∵AE+BE>AB,
∴AB<2CD.
故选:C.
10.解:如图,连接DB,DC,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵BC是直径,
∴∠BAC=90°,
∵BC=2,AB=2AC,
∴AC=2,AB=4,
∵∠DEA=∠EAF=∠DFA=90°,
∴四边形DEAF是矩形,
∵AD平分∠BAC,
∴DE=DF,
∴四边形DEAF是正方形,
∴AD=AF,
∵∠DAB=∠DAC,
∴=,
∴BD=CD,
∵∠DEB=∠F=90°,DB=DC,DE=DF,
∴Rt△DEB≌Rt△DFC(HL),
∴BE=CF,
∴AB+AC=AE+BE=AF﹣CF=2AF=6,
∴AF=3,
∴AD=AF=3,
故答案为:3.
11.解:∵⊙O中,弧AB的度数为50°,
∴弧AB所对的圆心角的度数为50°,
故答案为:50°.
12.解:在⊙O中,AC=BD,
∴∠AOC=∠BOD,
∴∠1+∠BOC=∠2+∠BOC,
∴∠1=∠2=30°.
故答案为:30°.
13.解:如图,连接OC、OD,
∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD=14°,
在△EDO中,∠ODC=∠E+∠EOD=28°,
∵OC=OD,
∴∠OCD=∠ODC=28°,
在△CEO中,∠AOC=∠E+∠OCD=14°+28°=42°,
∴弧AC的度数为42°.
故答案为:42°.
14.解:连接AB,AO,DO,
∵⊙O的弦AC=BD,
∴=,
∴=,
∴∠BAC=∠ABD,
∵AC⊥BD,
∴∠AEB=90°,
∴∠ABD=∠BAC=(180°﹣∠AEB)=45°,
∴∠AOD=2∠ABD=90°,
即△AOD是等腰直角三角形,
∵AD=3,AO2+OD2=AD2,
∴AO=3,
∴⊙O的周长是2×π×3=6π,
故答案为6π.
15.解:如图,连接OD,AC.
∵BA=BE=BC,
∴点B是△AEC的外接圆的圆心,
∴∠ACE=∠ABE=45°,
∴∠AOD=2∠ACE=90°,
∵OA=OD=5,
∴AD=5,
故答案为:5.
16.解:连接OB,如图,
∵OB=OC,OC=AB,
∴OB=AB,
∴∠A=∠BOA,
∴∠EBO=∠A+∠BOA=2∠A,
∵OB=OE,
∴∠E=∠EBO=2∠A,
∵∠EOD=∠E+∠A,
∴2∠A+∠A=84°,解得∠A=28°,
∴∠E=∠EBO=56°,
∴∠BOE=180°﹣∠E﹣∠EBO=180°﹣56°﹣56°=68°,
∴的度数为68°.
故答案为:68°.
17.解:连接AD,
∵∠BAC=90°,∠ABC=20°,
∴∠C=90°﹣∠ABC=70°,
∵AC=AD,
∴∠ADC=∠C=70°,
∴∠CAD=180°﹣∠C﹣∠ADC=40°,
∵∠CAB=90°,
∴∠DAE=90°﹣40°=50°,
∵AD=AE,
∴∠DEA=∠ADE=(180°﹣∠DAE)=65°.
18.证明:延长AD交⊙O于M,
∵BC⊥AD,BC过圆心O,
∴=,
∵=,
∴=,
∴∠BAF=∠ABF,
∴AF=BF.
19.证明:连接BD.
∵AB=CD,
∴=
∴﹣=﹣,即=,
∴∠B=∠D,
∴PB=PD.
20.解:连接OE,如图,
∵为30°,
∴∠COE=30°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣30°)÷2=75°,
∵弦CE∥AB,
∴∠AOC=∠OCE=75°.
1.如图所示的齿轮有16个齿,每两齿之间间隔相等,相邻两止间的圆心角α的度数为( )
A.20° B.22.5° C.25° D.30°
2.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙O的直径为15,则AC长为( )
A.10 B.13 C.12 D.11
3.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连结AB,AD,若AD=1,则R的值为( )
A. B. C.1 D.
4.将一个半径为1的圆形轮子沿直线l水平向右滚动,图中显示的是轮子上的点P的起始位置与终止位置,其中在起始位置时PO∥l,在终止位置时PO与l所夹锐角为60°,则滚动前后,圆心之间的距离可能为( )
A. B. C.π D.
5.如图,半径为5的⊙O中,有两条互相垂直的弦AB、CD,垂足为点E,且AB=CD=8,则OE的长为( )
A.3 B. C.2 D.3
6.在半径为1的⊙O中,若弦AB的长为1,则弦AB所对的圆心角的度数为( )
A.90° B.60° C.30° D.15°
7.如图,MN是⊙O的直径,点A是半圆上一个三等分点,点B是的中点,点B'是点B关于MN的对称点,⊙O的半径为1,则AB'的长等于( )
A.1 B. C. D.2
8.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④+=+,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
9.在⊙O中,如果=2.那么弦AB与弦CD之间的关系是( )
A.AB=2CD B.AB>2CD C.AB<2CD D.无法确定
10.如图,在⊙O中,AC=AB,直径BC=2,,则AD= .
11.在⊙O中,弧AB的度数为50°,则弧AB所对的圆心角的度数为 .
12.如图,在⊙O中,AC=BD,∠1=30°,则∠2的度数为 .
13.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=14°,则弧AC的度数为 °.
14.如图,⊙O的弦AC=BD,且AC⊥BD于E,连接AD,若AD=3,则⊙O的周长为 .
15.已知四边形ABCD内接于⊙O,OA=5,AB=BC,E为CD上一点,且BE=BC,∠ABE=90°,则AD的长为 .
16.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,求的度数.
17.如图,在Rt△ABC中,∠BAC=90°,点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.若∠ABC=20°,求∠DEA的度数.
18.如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,BE交AD于点F,且=,求证:AF=BF.
19.如图,⊙O的弦AB、CD相交于点P,且AB=CD.求证PB=PD.
20.如图,AB、CD是⊙O的直径,弦CE∥AB,所对的圆心角为30°.求∠AOC的度数.
参考答案
1.解:由题意这是正十六边形,中心角α==22.5°,
故选:B.
2.解:连接OF,
∵DE⊥AB,AB过圆心O,
∴DE=EF,=,
∵D为弧AC的中点,
∴=,
∴=,
∴AC=DF,
∵⊙O的直径为15,
∴OF=OA=,
∵AE=3,
∴OE=OA﹣AE=,
在Rt△OEF中,由勾股定理得:EF===6,
∴DE=EF=6,
∴AC=DF=DE+EF=6+6=12,
故选:C.
3.解:∵弦AC=BD,
∴=,
∴=,
∴∠ABD=∠BAC,
∴AE=BE;
如图,连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=1,
∴R=,
故选:B.
4.解:由题意可得,圆形轮子可能滚动不止一周,设OP滚动了n周后又滚动120°后到达终止位置,
∴OP滚动的角度α=120°+360n,n为整数,
可得圆心运动前后的距离即为OP滚动完毕扫过的角度所对应的弧长,
即为2πr×=,n为整数.
当n=0时为.
故选:B.
5.解:如图,作OM⊥AB于M,ON⊥CD于N,连接OA,OC.
∴AM=BM=4,CN=DN=4,
∵OA=OC=5,
∴OM===3,ON===3,
∴OM=ON,
∵AB⊥CD,
∴∠OME=∠ONE=∠MEN=90°,
∴四边形OMEN是矩形,
∵OM=ON,
∴四边形OMEN是正方形,
∴OE=OM=3,
故选:D.
6.解:∵在半径为1的⊙O中,弦AB的长为1,
∴OA=OB=AB=1,
∴△OAB为等边三角形,
∴弦AB所对的圆心角的度数为60°.
故选:B.
7.解:连接OB、OB′,
∵点A是半圆上一个三等分点,
∴∠AON=60°,
∵点B是的中点,
∴∠BON=30°,
∵点B'是点B关于MN的对称点,
∴∠B′ON=30°,
∴∠AOB′=90°,
∴AB′==,
故选:B.
8.解:∵F为的中点,
∴=,故①正确,
∴∠FCM=∠FAC,
∵∠ACF=∠ACM+∠MCF,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴=,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴的度数+的度数=180°,
∴的度数+的度数=180°,
∴+=+=+=+,故④正确,
故选:C.
9.解:取的中点E,连接AE,BE,
则=,
∵=2,
∴==,
∴CD=AE=BE,
∵AE+BE>AB,
∴AB<2CD.
故选:C.
10.解:如图,连接DB,DC,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵BC是直径,
∴∠BAC=90°,
∵BC=2,AB=2AC,
∴AC=2,AB=4,
∵∠DEA=∠EAF=∠DFA=90°,
∴四边形DEAF是矩形,
∵AD平分∠BAC,
∴DE=DF,
∴四边形DEAF是正方形,
∴AD=AF,
∵∠DAB=∠DAC,
∴=,
∴BD=CD,
∵∠DEB=∠F=90°,DB=DC,DE=DF,
∴Rt△DEB≌Rt△DFC(HL),
∴BE=CF,
∴AB+AC=AE+BE=AF﹣CF=2AF=6,
∴AF=3,
∴AD=AF=3,
故答案为:3.
11.解:∵⊙O中,弧AB的度数为50°,
∴弧AB所对的圆心角的度数为50°,
故答案为:50°.
12.解:在⊙O中,AC=BD,
∴∠AOC=∠BOD,
∴∠1+∠BOC=∠2+∠BOC,
∴∠1=∠2=30°.
故答案为:30°.
13.解:如图,连接OC、OD,
∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD=14°,
在△EDO中,∠ODC=∠E+∠EOD=28°,
∵OC=OD,
∴∠OCD=∠ODC=28°,
在△CEO中,∠AOC=∠E+∠OCD=14°+28°=42°,
∴弧AC的度数为42°.
故答案为:42°.
14.解:连接AB,AO,DO,
∵⊙O的弦AC=BD,
∴=,
∴=,
∴∠BAC=∠ABD,
∵AC⊥BD,
∴∠AEB=90°,
∴∠ABD=∠BAC=(180°﹣∠AEB)=45°,
∴∠AOD=2∠ABD=90°,
即△AOD是等腰直角三角形,
∵AD=3,AO2+OD2=AD2,
∴AO=3,
∴⊙O的周长是2×π×3=6π,
故答案为6π.
15.解:如图,连接OD,AC.
∵BA=BE=BC,
∴点B是△AEC的外接圆的圆心,
∴∠ACE=∠ABE=45°,
∴∠AOD=2∠ACE=90°,
∵OA=OD=5,
∴AD=5,
故答案为:5.
16.解:连接OB,如图,
∵OB=OC,OC=AB,
∴OB=AB,
∴∠A=∠BOA,
∴∠EBO=∠A+∠BOA=2∠A,
∵OB=OE,
∴∠E=∠EBO=2∠A,
∵∠EOD=∠E+∠A,
∴2∠A+∠A=84°,解得∠A=28°,
∴∠E=∠EBO=56°,
∴∠BOE=180°﹣∠E﹣∠EBO=180°﹣56°﹣56°=68°,
∴的度数为68°.
故答案为:68°.
17.解:连接AD,
∵∠BAC=90°,∠ABC=20°,
∴∠C=90°﹣∠ABC=70°,
∵AC=AD,
∴∠ADC=∠C=70°,
∴∠CAD=180°﹣∠C﹣∠ADC=40°,
∵∠CAB=90°,
∴∠DAE=90°﹣40°=50°,
∵AD=AE,
∴∠DEA=∠ADE=(180°﹣∠DAE)=65°.
18.证明:延长AD交⊙O于M,
∵BC⊥AD,BC过圆心O,
∴=,
∵=,
∴=,
∴∠BAF=∠ABF,
∴AF=BF.
19.证明:连接BD.
∵AB=CD,
∴=
∴﹣=﹣,即=,
∴∠B=∠D,
∴PB=PD.
20.解:连接OE,如图,
∵为30°,
∴∠COE=30°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣30°)÷2=75°,
∵弦CE∥AB,
∴∠AOC=∠OCE=75°.
