2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册 5.2.1基本初等函数的导数课件(共45张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册 5.2.1基本初等函数的导数课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 49.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 00:00:00 | ||
图片预览











文档简介
(共45张PPT)
讲课老师:关老师
5.2.1基本初等函数的导数
学习目标
掌握基本初等函数的导数公式,并能进行简单的应用
掌握几个常用函数的导数
经过前面的学习,相信你已经了解了什么是导数,那本节课我们就来研究一下,不同的函数该如何求导,我们将要学习一连串的导数公式,学完之后,就不用麻烦的定义去求导了,直接套公式就可以求出倒数了,怎么样?是不是很心动?那就开心的学习起来吧!
首先我们就来先学习一下幂函数的导数公式
一.幂函数的导数公式
我们先来看一下幂函数的导数公式,再来用最简单的方法来看一下幂函数怎么求导。
一.幂函数的导数公式
将幂函数的小指数复制到到x的前面,并且在指数上自动减1.
′
′
小牛试刀
那接下来我们来看一下幂函数导数公式的证明,因为涉及到选择性必修三中的二项式定理,所以我们就简单了解一下就可以。
二.正弦函数和余弦函数的导数公式
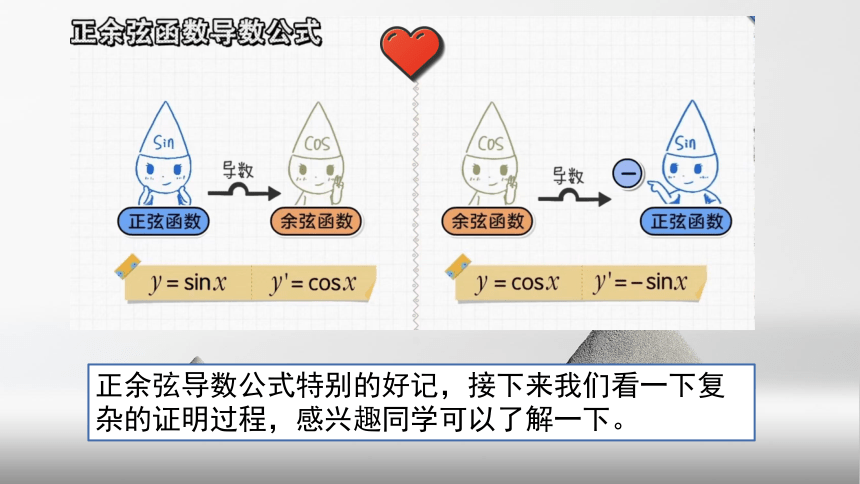
接下来我们学习两个关系十分密切的导数公式,就是正弦函数和余弦函数,首先我们来看一下导数公式。
正余弦导数公式特别的好记,接下来我们看一下复杂的证明过程,感兴趣同学可以了解一下。
小牛试刀
三.指数函数和对数函数的导数公式
这两个函数的导数公式,在形式和证明上有很多相似的地方,把他们放在一块,有助于大家理解。
我们先来看一下指数函数的导数公式,再来用最简单的方法来看一下指数函数怎么求导。
三.指数函数和对数函数的导数公式
三.指数函数和对数函数的导数公式
小牛试刀
指数函数的导函数的推导过程远远超出了高中知识,我们现在在课堂上推不了,所以就看特殊情况,当a=e时的推导过程。
我们先来看一下对数函数的导数公式,再来用最简单的方法来看一下对数函数怎么求导。
小牛试刀
对数函数的导函数的推导过程也远远超出了高中知识,我们现在在课堂上都推不了,所以就看特殊情况,当a=e时的推导过程。
四.常数函数的导数公式
常数函数,垂直于y轴的直线,斜率都为0,由导数的定义容易得到
所有常数函数的导数都为0!!!
总结 基本初等函数的导数公式
原函数 导函数
f(x)=c(c为常数) f′(x)=0
f(x)=xα(α∈Q,且α≠0) f′(x)=
f(x)=sin x f′(x)=
f(x)=cos x f′(x)=
f(x)=ax(a>0,且a≠1) f′(x)=
f(x)=ex f′(x)=
αxα-1
cos x
-sin x
axln a
ex
几个常用函数的导数
1
2x
[分析] 首先观察函数解析式是否符合求导形式,若不符合可先将函数解析式化为基本初等函数的求导形式.
解决此类问题应充分利用切点满足的三个关系:一是切点坐标满足曲线方程;二是切点坐标满足对应切线的方程;三是切线的斜率是曲线在此切点处的导数值.
题型三 导数的简单综合应用
[例3] 已知两条曲线y=sin x,y=cos x,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.
[分析] 先设切点P(x0,y0),看两个函数在P(x0,y0)处的导数的积等于-1是否有解.
[解析] 由于y=sin x,y=cos x,设这两条曲线的一个公共点为P(x0,y0).∴两条曲线在P(x0,y0)处的斜率分别为k1=cos x0,k2=-sin x0.
若使两条切线互相垂直,必须cos x0·(-sin x0)=-1,
即sin x0·cos x0=1,也就是sin 2x0=2,这是不可能的.
∴两条曲线不存在公共点,使在这一点处的两条切线互相垂直.
[答案] C
[典例2] 曲线f(x)=2x在点(0,1)处的切线方程为________.
[解析] ∵f(x)=2x,∴f′(x)=2xln 2,
∴f′(0)=ln 2.
故所求切线方程为y-1=(x-0)ln 2,
即y=xln 2+1.
[答案] y=xln 2+1
课堂小结
你学到了
哪些新知识呢?
课堂小练习
讲课老师:关老师
5.2.1基本初等函数的导数
学习目标
掌握基本初等函数的导数公式,并能进行简单的应用
掌握几个常用函数的导数
经过前面的学习,相信你已经了解了什么是导数,那本节课我们就来研究一下,不同的函数该如何求导,我们将要学习一连串的导数公式,学完之后,就不用麻烦的定义去求导了,直接套公式就可以求出倒数了,怎么样?是不是很心动?那就开心的学习起来吧!
首先我们就来先学习一下幂函数的导数公式
一.幂函数的导数公式
我们先来看一下幂函数的导数公式,再来用最简单的方法来看一下幂函数怎么求导。
一.幂函数的导数公式
将幂函数的小指数复制到到x的前面,并且在指数上自动减1.
′
′
小牛试刀
那接下来我们来看一下幂函数导数公式的证明,因为涉及到选择性必修三中的二项式定理,所以我们就简单了解一下就可以。
二.正弦函数和余弦函数的导数公式
接下来我们学习两个关系十分密切的导数公式,就是正弦函数和余弦函数,首先我们来看一下导数公式。
正余弦导数公式特别的好记,接下来我们看一下复杂的证明过程,感兴趣同学可以了解一下。
小牛试刀
三.指数函数和对数函数的导数公式
这两个函数的导数公式,在形式和证明上有很多相似的地方,把他们放在一块,有助于大家理解。
我们先来看一下指数函数的导数公式,再来用最简单的方法来看一下指数函数怎么求导。
三.指数函数和对数函数的导数公式
三.指数函数和对数函数的导数公式
小牛试刀
指数函数的导函数的推导过程远远超出了高中知识,我们现在在课堂上推不了,所以就看特殊情况,当a=e时的推导过程。
我们先来看一下对数函数的导数公式,再来用最简单的方法来看一下对数函数怎么求导。
小牛试刀
对数函数的导函数的推导过程也远远超出了高中知识,我们现在在课堂上都推不了,所以就看特殊情况,当a=e时的推导过程。
四.常数函数的导数公式
常数函数,垂直于y轴的直线,斜率都为0,由导数的定义容易得到
所有常数函数的导数都为0!!!
总结 基本初等函数的导数公式
原函数 导函数
f(x)=c(c为常数) f′(x)=0
f(x)=xα(α∈Q,且α≠0) f′(x)=
f(x)=sin x f′(x)=
f(x)=cos x f′(x)=
f(x)=ax(a>0,且a≠1) f′(x)=
f(x)=ex f′(x)=
αxα-1
cos x
-sin x
axln a
ex
几个常用函数的导数
1
2x
[分析] 首先观察函数解析式是否符合求导形式,若不符合可先将函数解析式化为基本初等函数的求导形式.
解决此类问题应充分利用切点满足的三个关系:一是切点坐标满足曲线方程;二是切点坐标满足对应切线的方程;三是切线的斜率是曲线在此切点处的导数值.
题型三 导数的简单综合应用
[例3] 已知两条曲线y=sin x,y=cos x,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.
[分析] 先设切点P(x0,y0),看两个函数在P(x0,y0)处的导数的积等于-1是否有解.
[解析] 由于y=sin x,y=cos x,设这两条曲线的一个公共点为P(x0,y0).∴两条曲线在P(x0,y0)处的斜率分别为k1=cos x0,k2=-sin x0.
若使两条切线互相垂直,必须cos x0·(-sin x0)=-1,
即sin x0·cos x0=1,也就是sin 2x0=2,这是不可能的.
∴两条曲线不存在公共点,使在这一点处的两条切线互相垂直.
[答案] C
[典例2] 曲线f(x)=2x在点(0,1)处的切线方程为________.
[解析] ∵f(x)=2x,∴f′(x)=2xln 2,
∴f′(0)=ln 2.
故所求切线方程为y-1=(x-0)ln 2,
即y=xln 2+1.
[答案] y=xln 2+1
课堂小结
你学到了
哪些新知识呢?
课堂小练习
