1.3 带电粒子在匀强磁场中的运动 同步练习题(word版含答案)
文档属性
| 名称 | 1.3 带电粒子在匀强磁场中的运动 同步练习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 859.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-20 06:06:36 | ||
图片预览




文档简介
1.3 带电粒子在匀强磁场中的运动
一、单选题
1.如图所示,氕核和氘核分别垂直进入同一匀强磁场中做匀速圆周运动,则( )
A.氕核和氘核做圆周运动的周期之比为2∶1
B.若入射速率相等,氕核和氘核做圆周运动的角速度相同
C.若质量和速率的乘积相等,氕核和氘核的圆周半径相等
D.增大入射速率,它们的周期也会增大
2.如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度大小为B,∠A=60°,AO=a。在O点放置一个粒子源,可以向各个方向发射某种带负电的粒子,粒子的比荷为,发射速度大小都为v0,且满足v0=,发射方向由图中的角度θ表示。对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
A.粒子不可能打到A点
B.以θ=60°飞入的粒子在磁场中运动时间最短
C.以θ<30°飞入的粒子在磁场中运动的时间都相等
D.在AC边界上只有一半区域有粒子射出
3.如图所示,两个横截面分别为圆和正方形,但磁感应强度均相同的匀强磁场,圆的直径D等于正方形的边长,两个电子以相同的速度分别飞入两个磁场区域,速度方向均与磁场方向垂直。进入圆形区域的电子速度方向对准了圆心,进入正方形区域的电子是沿一边的中心且垂直于边界线进入的,则( )
A.两个电子在磁场中运动的半径一定相同
B.两电子在磁场中运动的时间不可能相同
C.进入正方形区域的电子一定先飞离磁场
D.进入圆形区域的电子一定后飞离磁场
4.如图所示,半径为r圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入磁场,经过一段时间从C点射出磁场,OC与OB成60°角.则该粒子在磁场中运动的时间为( )
A. B. C. D.
5.如图所示,一重力不计的带电粒子以一定的速率从a点对准圆心射入一圆形匀强磁场,恰好从b点射出。减小粒子射入磁场的速率(速率不为0),下列判断正确的是( )
A.该粒子从ab间射出
B.该粒子从bc间射出
C.该粒子从ad间射出
D.该粒子从cd间射出
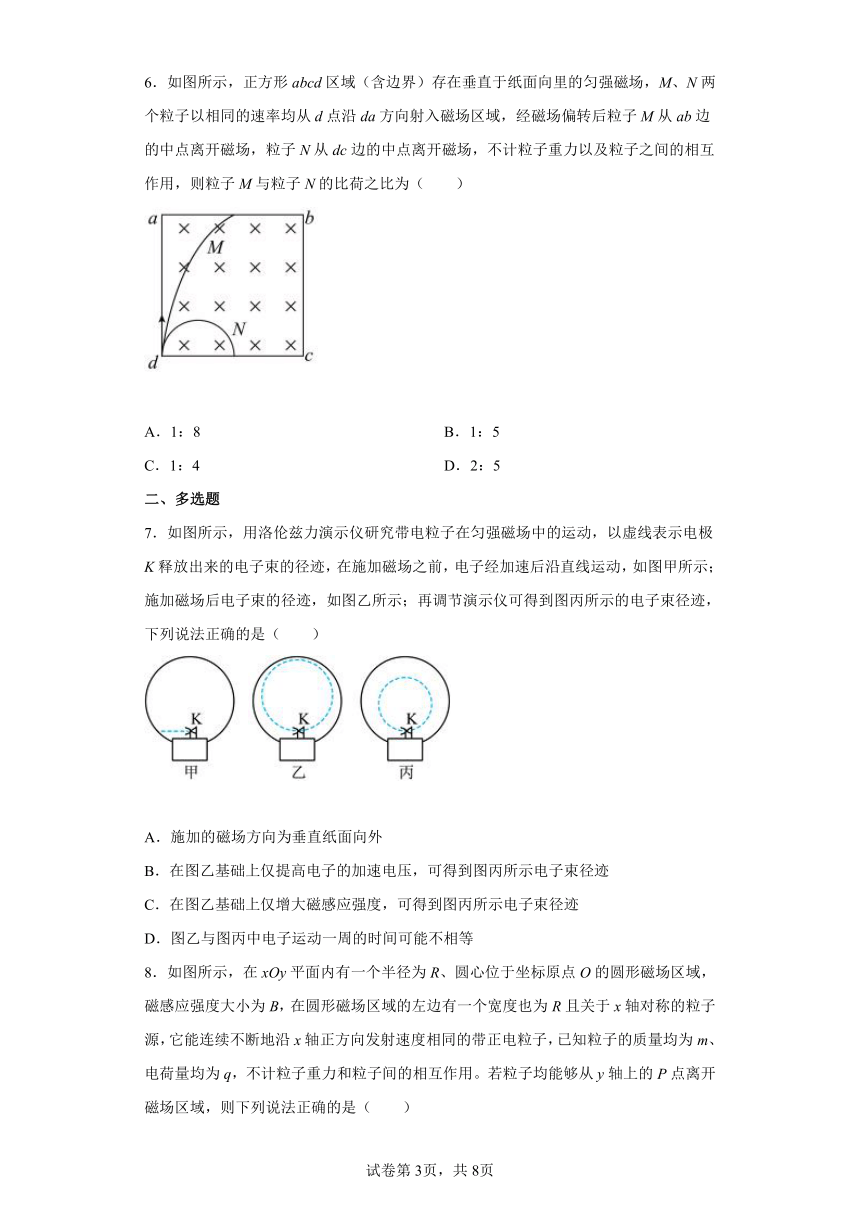
6.如图所示,正方形abcd区域(含边界)存在垂直于纸面向里的匀强磁场,M、N两个粒子以相同的速率均从d点沿da方向射入磁场区域,经磁场偏转后粒子M从ab边的中点离开磁场,粒子N从dc边的中点离开磁场,不计粒子重力以及粒子之间的相互作用,则粒子M与粒子N的比荷之比为( )
A.1:8 B.1:5
C.1:4 D.2:5
二、多选题
7.如图所示,用洛伦兹力演示仪研究带电粒子在匀强磁场中的运动,以虚线表示电极K释放出来的电子束的径迹,在施加磁场之前,电子经加速后沿直线运动,如图甲所示;施加磁场后电子束的径迹,如图乙所示;再调节演示仪可得到图丙所示的电子束径迹,下列说法正确的是( )
A.施加的磁场方向为垂直纸面向外
B.在图乙基础上仅提高电子的加速电压,可得到图丙所示电子束径迹
C.在图乙基础上仅增大磁感应强度,可得到图丙所示电子束径迹
D.图乙与图丙中电子运动一周的时间可能不相等
8.如图所示,在xOy平面内有一个半径为R、圆心位于坐标原点O的圆形磁场区域,磁感应强度大小为B,在圆形磁场区域的左边有一个宽度也为R且关于x轴对称的粒子源,它能连续不断地沿x轴正方向发射速度相同的带正电粒子,已知粒子的质量均为m、电荷量均为q,不计粒子重力和粒子间的相互作用。若粒子均能够从y轴上的P点离开磁场区域,则下列说法正确的是( )
A.磁场方向垂直xOy平面向外
B.粒子的速度大小为
C.粒子在磁场中运动的最长时间与最短时间的差值为
D.粒子从P点离开磁场时与x轴正方向的夹角的范围为
9.一磁感应强度大小为B、方向垂直纸面向外的有界匀强磁场分布在如图所示的圆环内,圆环内径R1A.粒子沿逆时针方向做圆周运动,轨道半径为a
B.若,则粒子能进入磁场内边界
C.若,则粒子在磁场中的运动时间为
D.若,调节磁感应强度大小为时,粒子从A点以任何方向入射都不能进入磁场内边界
10.如图所示,半径为r的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B,磁场边界上P点有一粒子,源源不断地向磁场发射各种方向(均平行于纸面)且速度大小相等的带正电的粒子(重力不计)。已知粒子的比荷为k,当粒子速度的大小为时,关于粒子的运动,以下说法正确的是( )
A.圆形磁场区域边界的三分之一弧长有粒子经过
B.圆形磁场区域边界的六分之一弧长有粒子经过
C.若增大粒子的射入速度,则有可能使所有粒子都以相同的方向射出磁场
D.若减小粒子的射入速度,则有可能使所有粒子都以相同的方向射出磁场
11.如图所示,直线与水平面成角,的右上方存在垂直纸面向外的匀强磁场,左下方存在垂直纸面向里的匀强磁场,两磁场的磁感应强度大小均为B.一粒子源位于a点,能水平向右发射不同速率、比荷为k的带正电粒子.已知a、b两点间的距离为L,不计带电粒子受到的重力,若所有带电粒子均能通过b点,则粒子的速度可能为( )
A. B. C. D.
三、填空题
12.如图所示,正方形边长为L,内有垂直纸面向外的匀强磁场,磁感应强度为B,现有质量为m、带电荷量为+q的粒子以速度v从ad边中点的小孔垂直于ad边射入匀强磁场,欲使粒子能打到cd边上,则磁感应强度B的取值范围是________.
13.如图所示,将截面为正方形的真空腔abcd放置在一匀强磁场中,磁场方向垂直纸面向里.若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上被吸收,则由小孔c和d射出的电子的速率之比________;通过磁场的时间之比为________ .
14.带电粒子A(质量为m、电量为q)和带电粒子B(质量为4m、电量为2q).垂直磁感线射入同一匀强磁场中(不计重力),若以相同速度入射,则轨道半径之比Ra:Rb=______,周期之比Ta:Tb=______.
四、解答题
15.如图所示,在第I象限内的虚线OC(OC与y轴正方向的夹角)与y轴所夹区域内(包括虚线OC)有磁感应强度大小为B、方向垂直于xOy平面向外的匀强磁场,大量质量为m、电荷量为q的带正电粒子(视为质点)从y轴上坐标为(0,L)的A点平行于x轴正方向射入磁场。取,不计粒子所受重力。
(1)若a粒子垂直y轴离开磁场,求其初速度大小v应满足的条件;
(2)若b粒子离开磁场后垂直经过x轴,求b粒子在第I象限内运动的时间t;
(3)若在(2)中情况下,在xOy平面内x轴与虚线OC所夹区域加上方向平行OC的匀强电场(图中未画出)结果b粒子恰好能到达x轴,求所加电场的电场强度大小E以及b粒子到达x轴上的位置的横坐标(不考虑b粒子到达x轴后的运动)。
16.真空中有一匀强磁场,磁场边界为两个半径分别为a和的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图.己知电子质量为m,电荷量为e,忽略重力。()
(1)若电子以速率v,从实线圆外沿半径方向射入磁场,为使电子不能进入内部无磁场区域,求磁场的磁感应强度最小值;
(2)若电子以速率v,从圆心沿半径方向进入磁场,为使该电子的运动能被限制在图中实线圆围成的区域内,求磁场的磁感应强度最小;
(3)在上述(1)、(2)两问中,带电粒子第一次在磁场中运动的时间之比。
17.如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xOy平面并指向纸面外,磁感应强度为B,一带正电的粒子以速度v0沿y 轴负方向从O点射入磁场,入射方向在xOy平面内,再回到x轴的交点到O的距离为L,求:
(1)该粒子的比荷
(2)如果粒子的入射方向与x轴正向的夹角为θ。则在磁场运动过程中与x 轴的最远距离d和带电粒子在磁场中运动的时间t
18.如图,两足够长的平行竖直线MN、PQ间距为d,其间存在竖直向下、电场强度大小为E的匀强电场和垂直于纸面向里、磁感应强度大小为B的匀强磁场。MN上有一粒子源A,能向各个方向射出电荷量相同、质量均为M、速率均为v0的微粒,且微粒恰好能在MN、PQ间做匀速圆周运动。当微粒的入射方向与MN的夹角为时,微粒恰好沿垂直于PQ的方向射出,重力加速度为g,已知,≈1.414。求:
(1)微粒的电荷量及电性;
(2)微粒的速率v0;
(3)从PQ射出的微粒做匀速圆周运动的最短时间t。
试卷第1页,共3页
试卷第8页,共8页
参考答案:
1.C
【解析】
【详解】
A.粒子在磁场中做圆周运动的周期
代入氕核和氘核的比荷得氕核和氘核做圆周运动的周期之比为1:2,A错误;
B.粒子在磁场中做圆周运动的半径
,
氕核和氘核的角速度大小之比为2:1,与入射速率无关,B错误;
C.由
可知,若质量和速率的乘积相等,氕核和氘核的圆周半径相等,C正确;
D.入射速率与周期无关,所以增大入射速率,它们的周期也不变,D错误。
故选C。
2.D
【解析】
【详解】
A.由牛顿第二定律
得
解得:R=a,因此当θ=60°入射时,粒子恰好从A点飞出,见图1,故A错误;
B.当θ=60°飞入的粒子在磁场中运动时对应的弦长为a,对应的时间为,不管是从OA段射出,还是从AC段射出,这个弦长都是最大弦长,最大的弦长就对应着最大的弧长,而速度大小不变,所以弧长越大时间越长,即这个时间是最长时间,故B错误;
C.当θ=0°飞入的粒子在磁场中,粒子恰好从AC中点飞出,见图2,在磁场中运动时间也恰好是,所以:θ从0°到60°在磁场中运动时间先减小后增大,故C错误;
D.当θ=0°飞入的粒子在磁场中,粒子恰好从AC中点飞出,见图2,因此在AC边界上只有一半区域有粒子射出,故D正确。
故选D。
3.A
【解析】
【详解】
A.电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,有
整理得
两个过程电子的速度v相同,所以半径R相同,选项A正确;
BCD.由于它们进入圆形磁场和正方形磁场的速度、轨迹半径是相同的,我们把圆形磁场和正方形磁场放到同一位置如图所示:
由图可以看出若进入磁场区域的电子的轨迹为1,先出圆形磁场,再出正方形磁场;若进入磁场区域的电子的轨迹为2,同时从圆形与正方形边界出磁场,运动时间相同;若进入磁场区域的电子的轨迹为3,先出圈形磁场,再出正方形磁场。可知选项BCD错误。
故选A。
4.A
【解析】
【详解】
粒子在磁场中运动的半径
时间为
故选A。
5.A
【解析】
【详解】
由左手定则知,该粒子带负电, 由
解得
知减小粒子射入磁场的速率,带电粒子的运动半径减小,故粒子从ab间射出。
故选A。
6.B
【解析】
【详解】
作出粒子的运动轨迹如图
设正方形边长为L,粒子沿da方向射入磁场区域,粒子N从dc边的中点离开磁场,则粒子N的半径
粒子M从ab边的中点离开磁场,由图可知
由几何关系可知
解得
根据洛伦兹力提供向心力有
解得粒子的比荷
所以粒子M与粒子N的比荷之比为
故选B。
7.CD
【解析】
【详解】
A.根据左手定则,施加的磁场方向为垂直纸面向里,A错误;
BC.根据动能定理
根据牛顿第二定律
解得
在图乙基础上仅提高电子的加速电压,电子的轨道半径增大,不能得到图丙所示电子束径迹,B错误;在图乙基础上仅增大磁感应强度,电子的轨道半径减小,可得到图丙所示电子束径迹,C正确;
D.根据
图乙与图丙中的磁感应强度可能不相同,电子运动一周的时间可能不相等,D正确。
故选CD。
8.BC
【解析】
【详解】
A.由于粒子均向上偏转,由左手定则可知,磁场方向垂直于xOy平面向里,故A错误;
B.由于粒子均能从P点离开磁场,由几何关系可知粒子在磁场中做圆周运动的轨迹半径也为R,由
qv0B=m
可知粒子的速度大小
v0=
故B正确;
C.在磁场中运动时间最长的粒子与运动时间最短的粒子的运动轨迹如图所示,
设粒子在磁场中运动的最长时间为t1,则有
t1==
同理粒子在磁场中运动的最短时间为
t2==
所以最大时间差为
Δt=t1-t2=
故C正确;
D.由几何关系可知,粒子离开磁场时与x轴正方向的夹角的范围应为
≤θ≤
故D错误。
故选BC。
9.CD
【解析】
【详解】
A.根据左手定则可以判断粒子沿顺时针方向做圆周运动,设轨道半径为r,根据牛顿第二定律有
解得
故A错误;
BC.若,作出粒子运动轨迹如图1所示。根据几何关系可知
粒子运动轨迹到磁场内边界的最小距离为
所以粒子不可能进入磁场内边界。
粒子在磁场中运动的周期为
根据几何关系可知粒子转过的圆心角为120°,所以粒子在磁场中的运动时间为
故B错误,C正确;
图1
D.若,调节磁感应强度大小为时,粒子的运动半径为
如图2所示,当粒子入射速度方向与外边界相切时,粒子运动轨迹到内边界的最近距离为
此时粒子从A点以任何方向入射都不能进入磁场内边界,故D正确。
故选CD。
图2
10.BC
【解析】
【详解】
AB.设粒子在磁场中做匀速圆周运动的半径为R,根据牛顿第二定律有
解得
离P点最远的粒子出射点到P点的距离为轨迹的直径,长度为r,如图所示,根据几何关系可知圆形磁场区域边界的六分之一弧长有粒子经过,故A错误,B正确;
CD.当粒子的射入速度增大至kBr时,易知此时粒子的运动半径等于R,如图所示,对于以任意方向入射的粒子,其出射点为Q,轨迹圆心为O′,根据几何关系可推知此时四边形POQO′为菱形,则出射速度方向垂直于PO,由此可知粒子出射方向与入射方向无关,所以若增大粒子的射入速度,则有可能使所有粒子都以相同的方向射出磁场,故C正确,D错误。
故选BC。
11.BC
【解析】
【详解】
粒子可能在两磁场间做多次运动,画出可能的粒子,如图,所有圆弧的圆心角都是,根据几何关系可得粒子运动的半径为
(n=1,2,3…)
根据洛伦兹力提供向心力可得
带电粒子比荷为k的带正电粒子,联立解得
,n=1,2,3…
AD错误,BC正确。
故选BC。
12.
【解析】
【详解】
由题意知,带正电的粒子从cd边d点射出磁场,其在磁场中圆周运动的半径,故粒子在磁场中做圆周运动洛伦兹力提供向心力即,可得粒子做圆周运动的磁感应强度;
带正电的粒子从cd边c点射出磁场,由几何关系可知:,可得粒子圆周运动的最大半径,故粒子在磁场中做圆周运动洛伦兹力提供向心力即,可得粒子做圆周运动的磁感应强度;
故欲使粒子打在cd边上,磁感应强度B的取值范围是.
13. 2:1 1:2
【解析】
【分析】
电子垂直射入匀强磁场中,由洛伦兹力提供向心力,做匀速圆周运动.根据牛顿第二定律推导出电子圆周运动的速率与半径的关系.根据几何知识确定电子从c孔和b孔时半径关系,求解速率之比.根据时间与周期的关系,求解时间之比.
【详解】
设电子的质量为m,电量为q,磁感应强度为B,电子圆周运动的半径为r,速率为v,
由牛顿第二定律得:
evB=m
解得:
r与v成正比.由图看出,从c孔和d孔射出的电子半径之比rc:rd=2:1,则速率之比
vc:vd=rc:rd=2:1.
电子圆周运动的周期为:
所有电子的周期相等,从c孔和d孔射出的电子在盒内运动时间分别为:
tc=T
td=T
所以从c孔和d孔射出的电子在盒内运动时间之比:
tc:td=1:2;
【点睛】
本题属于带电粒子在磁场中的偏转中典型题目,此类题的关键在于确定圆心及由几何关系求出半径.知道半径和周期的表达式;
14. 1:2 1:2
【解析】
【分析】
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出粒子轨道半径,然后根据粒子轨道半径公式、周期公式.
【详解】
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:,解得:,则:;
粒子做圆周运动的周期:,周期之比:;
【点睛】
本题考查了带电粒子在磁场中的运动,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,应用牛顿第二定律求出粒子做圆周运动的轨迹半径,根据轨道半径公式与周期公式可以解题.
15.(1);(2);(3);
【解析】
【详解】
(1)当a粒子在磁场中的运动轨迹对应的圆心角为180°时,a粒子垂直y轴离开磁场,在此种情况下,当a粒子的运动轨迹与OC相切时,a粒子的初速度最大(设为),如图甲所示。
设此时a粒子在磁场中运动的轨迹半径为,有
根据几何关系有
解得
v应满足的条件为
(2)b粒子运动四分之一圆周后离开磁场,将垂直经过x轴,运动轨迹如图乙所示
设轨迹圆的半径为,有
根据几何关系有
解得
b点粒子在磁场中做圆周运动的周期
b粒子在磁场中运动的时间
解得
根据几何关系,b粒子经过虚线OC时到x轴的距离
设b粒子离开磁场后在第I象限内运动的时间为,有
又
解得
(3)b粒子沿y轴方向的加速度大小
根据匀变速直线运动的规律有
解得
b粒子沿x轴方向的加速度大小
设b粒子从虚线OC运动到x轴的时间为,有
b粒子从虚线OC运动到x轴的过程中沿x轴方向的位移大小
又
解得
16.(1);(2);(3)
【解析】
【详解】
(1)电子在磁场中作匀速圆周运动,由洛伦兹力提供向心力
①
则磁感应强度与圆周运动轨迹关系为
②
即运动轨迹半径越大,磁场的磁感应强度越小。
从实线圆外沿半径方向射入磁场,当磁感应强度为B1时电子恰好与内圆柱面相切而没有进入内部无磁场区域,则此时的B1即为题目要求的磁感应强度最小值。作图如下,设电子从A点沿半径方向射入磁场,从B点射出磁场,O’为轨迹圆的圆心。
对,由几何关系可得
③
解得
R1=4a
带入②式可得
(2)为了使电子的运动被限制在图中实线圆围成的区域内,其最大半径的运动轨迹与实线圆相切,此时的B2即为题目要求的磁感应强度最小值;令此半径为r,如图所示
A点为电子做圆周运动的圆心,电子从圆心沿半径方向进入磁场,由左手定则可得,,为直角三角形,则由几何关系可得
④
可得
带入②式可得
(3)上述(1)中,由几何关系可知电子在磁场中运动的圆弧对应的圆心角 ,在(2)中,电子在磁场中运动的圆弧对应的圆心角
由圆周运动周期公式 带入①式可得
⑤
电子在磁场中运动的时间与圆心角即周期的关系是
⑥
所以(1)、(2)两种情况电子在磁场中运动的时间之比为
带入数据可得
17.(1);(2),
【解析】
【详解】
(1)几何关系得
圆周运动
解得比荷
(2)根据几何关系可得
解得
运动时间
周期
解得
18.(1),负电;(2);(3)
【解析】
【详解】
(1)微粒在空间中受到三个力的作用:重力、电场力和洛伦兹力,由于微粒恰好能做匀速圆周运动,则
微粒带负电
解得
(2)当微粒的入射方向与MN的夹角为时,微粒的运动轨迹如图所示
由几何关系易得,微粒运动的半径
则由
解得
(3)当对应弦长为d时,做匀速圆周运动的时间最短,微粒的运动轨迹如图所示
由几何关系
解得
根据
最短时间
答案第1页,共2页
答案第20页,共1页
一、单选题
1.如图所示,氕核和氘核分别垂直进入同一匀强磁场中做匀速圆周运动,则( )
A.氕核和氘核做圆周运动的周期之比为2∶1
B.若入射速率相等,氕核和氘核做圆周运动的角速度相同
C.若质量和速率的乘积相等,氕核和氘核的圆周半径相等
D.增大入射速率,它们的周期也会增大
2.如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度大小为B,∠A=60°,AO=a。在O点放置一个粒子源,可以向各个方向发射某种带负电的粒子,粒子的比荷为,发射速度大小都为v0,且满足v0=,发射方向由图中的角度θ表示。对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
A.粒子不可能打到A点
B.以θ=60°飞入的粒子在磁场中运动时间最短
C.以θ<30°飞入的粒子在磁场中运动的时间都相等
D.在AC边界上只有一半区域有粒子射出
3.如图所示,两个横截面分别为圆和正方形,但磁感应强度均相同的匀强磁场,圆的直径D等于正方形的边长,两个电子以相同的速度分别飞入两个磁场区域,速度方向均与磁场方向垂直。进入圆形区域的电子速度方向对准了圆心,进入正方形区域的电子是沿一边的中心且垂直于边界线进入的,则( )
A.两个电子在磁场中运动的半径一定相同
B.两电子在磁场中运动的时间不可能相同
C.进入正方形区域的电子一定先飞离磁场
D.进入圆形区域的电子一定后飞离磁场
4.如图所示,半径为r圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入磁场,经过一段时间从C点射出磁场,OC与OB成60°角.则该粒子在磁场中运动的时间为( )
A. B. C. D.
5.如图所示,一重力不计的带电粒子以一定的速率从a点对准圆心射入一圆形匀强磁场,恰好从b点射出。减小粒子射入磁场的速率(速率不为0),下列判断正确的是( )
A.该粒子从ab间射出
B.该粒子从bc间射出
C.该粒子从ad间射出
D.该粒子从cd间射出
6.如图所示,正方形abcd区域(含边界)存在垂直于纸面向里的匀强磁场,M、N两个粒子以相同的速率均从d点沿da方向射入磁场区域,经磁场偏转后粒子M从ab边的中点离开磁场,粒子N从dc边的中点离开磁场,不计粒子重力以及粒子之间的相互作用,则粒子M与粒子N的比荷之比为( )
A.1:8 B.1:5
C.1:4 D.2:5
二、多选题
7.如图所示,用洛伦兹力演示仪研究带电粒子在匀强磁场中的运动,以虚线表示电极K释放出来的电子束的径迹,在施加磁场之前,电子经加速后沿直线运动,如图甲所示;施加磁场后电子束的径迹,如图乙所示;再调节演示仪可得到图丙所示的电子束径迹,下列说法正确的是( )
A.施加的磁场方向为垂直纸面向外
B.在图乙基础上仅提高电子的加速电压,可得到图丙所示电子束径迹
C.在图乙基础上仅增大磁感应强度,可得到图丙所示电子束径迹
D.图乙与图丙中电子运动一周的时间可能不相等
8.如图所示,在xOy平面内有一个半径为R、圆心位于坐标原点O的圆形磁场区域,磁感应强度大小为B,在圆形磁场区域的左边有一个宽度也为R且关于x轴对称的粒子源,它能连续不断地沿x轴正方向发射速度相同的带正电粒子,已知粒子的质量均为m、电荷量均为q,不计粒子重力和粒子间的相互作用。若粒子均能够从y轴上的P点离开磁场区域,则下列说法正确的是( )
A.磁场方向垂直xOy平面向外
B.粒子的速度大小为
C.粒子在磁场中运动的最长时间与最短时间的差值为
D.粒子从P点离开磁场时与x轴正方向的夹角的范围为
9.一磁感应强度大小为B、方向垂直纸面向外的有界匀强磁场分布在如图所示的圆环内,圆环内径R1
B.若,则粒子能进入磁场内边界
C.若,则粒子在磁场中的运动时间为
D.若,调节磁感应强度大小为时,粒子从A点以任何方向入射都不能进入磁场内边界
10.如图所示,半径为r的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B,磁场边界上P点有一粒子,源源不断地向磁场发射各种方向(均平行于纸面)且速度大小相等的带正电的粒子(重力不计)。已知粒子的比荷为k,当粒子速度的大小为时,关于粒子的运动,以下说法正确的是( )
A.圆形磁场区域边界的三分之一弧长有粒子经过
B.圆形磁场区域边界的六分之一弧长有粒子经过
C.若增大粒子的射入速度,则有可能使所有粒子都以相同的方向射出磁场
D.若减小粒子的射入速度,则有可能使所有粒子都以相同的方向射出磁场
11.如图所示,直线与水平面成角,的右上方存在垂直纸面向外的匀强磁场,左下方存在垂直纸面向里的匀强磁场,两磁场的磁感应强度大小均为B.一粒子源位于a点,能水平向右发射不同速率、比荷为k的带正电粒子.已知a、b两点间的距离为L,不计带电粒子受到的重力,若所有带电粒子均能通过b点,则粒子的速度可能为( )
A. B. C. D.
三、填空题
12.如图所示,正方形边长为L,内有垂直纸面向外的匀强磁场,磁感应强度为B,现有质量为m、带电荷量为+q的粒子以速度v从ad边中点的小孔垂直于ad边射入匀强磁场,欲使粒子能打到cd边上,则磁感应强度B的取值范围是________.
13.如图所示,将截面为正方形的真空腔abcd放置在一匀强磁场中,磁场方向垂直纸面向里.若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上被吸收,则由小孔c和d射出的电子的速率之比________;通过磁场的时间之比为________ .
14.带电粒子A(质量为m、电量为q)和带电粒子B(质量为4m、电量为2q).垂直磁感线射入同一匀强磁场中(不计重力),若以相同速度入射,则轨道半径之比Ra:Rb=______,周期之比Ta:Tb=______.
四、解答题
15.如图所示,在第I象限内的虚线OC(OC与y轴正方向的夹角)与y轴所夹区域内(包括虚线OC)有磁感应强度大小为B、方向垂直于xOy平面向外的匀强磁场,大量质量为m、电荷量为q的带正电粒子(视为质点)从y轴上坐标为(0,L)的A点平行于x轴正方向射入磁场。取,不计粒子所受重力。
(1)若a粒子垂直y轴离开磁场,求其初速度大小v应满足的条件;
(2)若b粒子离开磁场后垂直经过x轴,求b粒子在第I象限内运动的时间t;
(3)若在(2)中情况下,在xOy平面内x轴与虚线OC所夹区域加上方向平行OC的匀强电场(图中未画出)结果b粒子恰好能到达x轴,求所加电场的电场强度大小E以及b粒子到达x轴上的位置的横坐标(不考虑b粒子到达x轴后的运动)。
16.真空中有一匀强磁场,磁场边界为两个半径分别为a和的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图.己知电子质量为m,电荷量为e,忽略重力。()
(1)若电子以速率v,从实线圆外沿半径方向射入磁场,为使电子不能进入内部无磁场区域,求磁场的磁感应强度最小值;
(2)若电子以速率v,从圆心沿半径方向进入磁场,为使该电子的运动能被限制在图中实线圆围成的区域内,求磁场的磁感应强度最小;
(3)在上述(1)、(2)两问中,带电粒子第一次在磁场中运动的时间之比。
17.如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xOy平面并指向纸面外,磁感应强度为B,一带正电的粒子以速度v0沿y 轴负方向从O点射入磁场,入射方向在xOy平面内,再回到x轴的交点到O的距离为L,求:
(1)该粒子的比荷
(2)如果粒子的入射方向与x轴正向的夹角为θ。则在磁场运动过程中与x 轴的最远距离d和带电粒子在磁场中运动的时间t
18.如图,两足够长的平行竖直线MN、PQ间距为d,其间存在竖直向下、电场强度大小为E的匀强电场和垂直于纸面向里、磁感应强度大小为B的匀强磁场。MN上有一粒子源A,能向各个方向射出电荷量相同、质量均为M、速率均为v0的微粒,且微粒恰好能在MN、PQ间做匀速圆周运动。当微粒的入射方向与MN的夹角为时,微粒恰好沿垂直于PQ的方向射出,重力加速度为g,已知,≈1.414。求:
(1)微粒的电荷量及电性;
(2)微粒的速率v0;
(3)从PQ射出的微粒做匀速圆周运动的最短时间t。
试卷第1页,共3页
试卷第8页,共8页
参考答案:
1.C
【解析】
【详解】
A.粒子在磁场中做圆周运动的周期
代入氕核和氘核的比荷得氕核和氘核做圆周运动的周期之比为1:2,A错误;
B.粒子在磁场中做圆周运动的半径
,
氕核和氘核的角速度大小之比为2:1,与入射速率无关,B错误;
C.由
可知,若质量和速率的乘积相等,氕核和氘核的圆周半径相等,C正确;
D.入射速率与周期无关,所以增大入射速率,它们的周期也不变,D错误。
故选C。
2.D
【解析】
【详解】
A.由牛顿第二定律
得
解得:R=a,因此当θ=60°入射时,粒子恰好从A点飞出,见图1,故A错误;
B.当θ=60°飞入的粒子在磁场中运动时对应的弦长为a,对应的时间为,不管是从OA段射出,还是从AC段射出,这个弦长都是最大弦长,最大的弦长就对应着最大的弧长,而速度大小不变,所以弧长越大时间越长,即这个时间是最长时间,故B错误;
C.当θ=0°飞入的粒子在磁场中,粒子恰好从AC中点飞出,见图2,在磁场中运动时间也恰好是,所以:θ从0°到60°在磁场中运动时间先减小后增大,故C错误;
D.当θ=0°飞入的粒子在磁场中,粒子恰好从AC中点飞出,见图2,因此在AC边界上只有一半区域有粒子射出,故D正确。
故选D。
3.A
【解析】
【详解】
A.电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,有
整理得
两个过程电子的速度v相同,所以半径R相同,选项A正确;
BCD.由于它们进入圆形磁场和正方形磁场的速度、轨迹半径是相同的,我们把圆形磁场和正方形磁场放到同一位置如图所示:
由图可以看出若进入磁场区域的电子的轨迹为1,先出圆形磁场,再出正方形磁场;若进入磁场区域的电子的轨迹为2,同时从圆形与正方形边界出磁场,运动时间相同;若进入磁场区域的电子的轨迹为3,先出圈形磁场,再出正方形磁场。可知选项BCD错误。
故选A。
4.A
【解析】
【详解】
粒子在磁场中运动的半径
时间为
故选A。
5.A
【解析】
【详解】
由左手定则知,该粒子带负电, 由
解得
知减小粒子射入磁场的速率,带电粒子的运动半径减小,故粒子从ab间射出。
故选A。
6.B
【解析】
【详解】
作出粒子的运动轨迹如图
设正方形边长为L,粒子沿da方向射入磁场区域,粒子N从dc边的中点离开磁场,则粒子N的半径
粒子M从ab边的中点离开磁场,由图可知
由几何关系可知
解得
根据洛伦兹力提供向心力有
解得粒子的比荷
所以粒子M与粒子N的比荷之比为
故选B。
7.CD
【解析】
【详解】
A.根据左手定则,施加的磁场方向为垂直纸面向里,A错误;
BC.根据动能定理
根据牛顿第二定律
解得
在图乙基础上仅提高电子的加速电压,电子的轨道半径增大,不能得到图丙所示电子束径迹,B错误;在图乙基础上仅增大磁感应强度,电子的轨道半径减小,可得到图丙所示电子束径迹,C正确;
D.根据
图乙与图丙中的磁感应强度可能不相同,电子运动一周的时间可能不相等,D正确。
故选CD。
8.BC
【解析】
【详解】
A.由于粒子均向上偏转,由左手定则可知,磁场方向垂直于xOy平面向里,故A错误;
B.由于粒子均能从P点离开磁场,由几何关系可知粒子在磁场中做圆周运动的轨迹半径也为R,由
qv0B=m
可知粒子的速度大小
v0=
故B正确;
C.在磁场中运动时间最长的粒子与运动时间最短的粒子的运动轨迹如图所示,
设粒子在磁场中运动的最长时间为t1,则有
t1==
同理粒子在磁场中运动的最短时间为
t2==
所以最大时间差为
Δt=t1-t2=
故C正确;
D.由几何关系可知,粒子离开磁场时与x轴正方向的夹角的范围应为
≤θ≤
故D错误。
故选BC。
9.CD
【解析】
【详解】
A.根据左手定则可以判断粒子沿顺时针方向做圆周运动,设轨道半径为r,根据牛顿第二定律有
解得
故A错误;
BC.若,作出粒子运动轨迹如图1所示。根据几何关系可知
粒子运动轨迹到磁场内边界的最小距离为
所以粒子不可能进入磁场内边界。
粒子在磁场中运动的周期为
根据几何关系可知粒子转过的圆心角为120°,所以粒子在磁场中的运动时间为
故B错误,C正确;
图1
D.若,调节磁感应强度大小为时,粒子的运动半径为
如图2所示,当粒子入射速度方向与外边界相切时,粒子运动轨迹到内边界的最近距离为
此时粒子从A点以任何方向入射都不能进入磁场内边界,故D正确。
故选CD。
图2
10.BC
【解析】
【详解】
AB.设粒子在磁场中做匀速圆周运动的半径为R,根据牛顿第二定律有
解得
离P点最远的粒子出射点到P点的距离为轨迹的直径,长度为r,如图所示,根据几何关系可知圆形磁场区域边界的六分之一弧长有粒子经过,故A错误,B正确;
CD.当粒子的射入速度增大至kBr时,易知此时粒子的运动半径等于R,如图所示,对于以任意方向入射的粒子,其出射点为Q,轨迹圆心为O′,根据几何关系可推知此时四边形POQO′为菱形,则出射速度方向垂直于PO,由此可知粒子出射方向与入射方向无关,所以若增大粒子的射入速度,则有可能使所有粒子都以相同的方向射出磁场,故C正确,D错误。
故选BC。
11.BC
【解析】
【详解】
粒子可能在两磁场间做多次运动,画出可能的粒子,如图,所有圆弧的圆心角都是,根据几何关系可得粒子运动的半径为
(n=1,2,3…)
根据洛伦兹力提供向心力可得
带电粒子比荷为k的带正电粒子,联立解得
,n=1,2,3…
AD错误,BC正确。
故选BC。
12.
【解析】
【详解】
由题意知,带正电的粒子从cd边d点射出磁场,其在磁场中圆周运动的半径,故粒子在磁场中做圆周运动洛伦兹力提供向心力即,可得粒子做圆周运动的磁感应强度;
带正电的粒子从cd边c点射出磁场,由几何关系可知:,可得粒子圆周运动的最大半径,故粒子在磁场中做圆周运动洛伦兹力提供向心力即,可得粒子做圆周运动的磁感应强度;
故欲使粒子打在cd边上,磁感应强度B的取值范围是.
13. 2:1 1:2
【解析】
【分析】
电子垂直射入匀强磁场中,由洛伦兹力提供向心力,做匀速圆周运动.根据牛顿第二定律推导出电子圆周运动的速率与半径的关系.根据几何知识确定电子从c孔和b孔时半径关系,求解速率之比.根据时间与周期的关系,求解时间之比.
【详解】
设电子的质量为m,电量为q,磁感应强度为B,电子圆周运动的半径为r,速率为v,
由牛顿第二定律得:
evB=m
解得:
r与v成正比.由图看出,从c孔和d孔射出的电子半径之比rc:rd=2:1,则速率之比
vc:vd=rc:rd=2:1.
电子圆周运动的周期为:
所有电子的周期相等,从c孔和d孔射出的电子在盒内运动时间分别为:
tc=T
td=T
所以从c孔和d孔射出的电子在盒内运动时间之比:
tc:td=1:2;
【点睛】
本题属于带电粒子在磁场中的偏转中典型题目,此类题的关键在于确定圆心及由几何关系求出半径.知道半径和周期的表达式;
14. 1:2 1:2
【解析】
【分析】
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出粒子轨道半径,然后根据粒子轨道半径公式、周期公式.
【详解】
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:,解得:,则:;
粒子做圆周运动的周期:,周期之比:;
【点睛】
本题考查了带电粒子在磁场中的运动,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,应用牛顿第二定律求出粒子做圆周运动的轨迹半径,根据轨道半径公式与周期公式可以解题.
15.(1);(2);(3);
【解析】
【详解】
(1)当a粒子在磁场中的运动轨迹对应的圆心角为180°时,a粒子垂直y轴离开磁场,在此种情况下,当a粒子的运动轨迹与OC相切时,a粒子的初速度最大(设为),如图甲所示。
设此时a粒子在磁场中运动的轨迹半径为,有
根据几何关系有
解得
v应满足的条件为
(2)b粒子运动四分之一圆周后离开磁场,将垂直经过x轴,运动轨迹如图乙所示
设轨迹圆的半径为,有
根据几何关系有
解得
b点粒子在磁场中做圆周运动的周期
b粒子在磁场中运动的时间
解得
根据几何关系,b粒子经过虚线OC时到x轴的距离
设b粒子离开磁场后在第I象限内运动的时间为,有
又
解得
(3)b粒子沿y轴方向的加速度大小
根据匀变速直线运动的规律有
解得
b粒子沿x轴方向的加速度大小
设b粒子从虚线OC运动到x轴的时间为,有
b粒子从虚线OC运动到x轴的过程中沿x轴方向的位移大小
又
解得
16.(1);(2);(3)
【解析】
【详解】
(1)电子在磁场中作匀速圆周运动,由洛伦兹力提供向心力
①
则磁感应强度与圆周运动轨迹关系为
②
即运动轨迹半径越大,磁场的磁感应强度越小。
从实线圆外沿半径方向射入磁场,当磁感应强度为B1时电子恰好与内圆柱面相切而没有进入内部无磁场区域,则此时的B1即为题目要求的磁感应强度最小值。作图如下,设电子从A点沿半径方向射入磁场,从B点射出磁场,O’为轨迹圆的圆心。
对,由几何关系可得
③
解得
R1=4a
带入②式可得
(2)为了使电子的运动被限制在图中实线圆围成的区域内,其最大半径的运动轨迹与实线圆相切,此时的B2即为题目要求的磁感应强度最小值;令此半径为r,如图所示
A点为电子做圆周运动的圆心,电子从圆心沿半径方向进入磁场,由左手定则可得,,为直角三角形,则由几何关系可得
④
可得
带入②式可得
(3)上述(1)中,由几何关系可知电子在磁场中运动的圆弧对应的圆心角 ,在(2)中,电子在磁场中运动的圆弧对应的圆心角
由圆周运动周期公式 带入①式可得
⑤
电子在磁场中运动的时间与圆心角即周期的关系是
⑥
所以(1)、(2)两种情况电子在磁场中运动的时间之比为
带入数据可得
17.(1);(2),
【解析】
【详解】
(1)几何关系得
圆周运动
解得比荷
(2)根据几何关系可得
解得
运动时间
周期
解得
18.(1),负电;(2);(3)
【解析】
【详解】
(1)微粒在空间中受到三个力的作用:重力、电场力和洛伦兹力,由于微粒恰好能做匀速圆周运动,则
微粒带负电
解得
(2)当微粒的入射方向与MN的夹角为时,微粒的运动轨迹如图所示
由几何关系易得,微粒运动的半径
则由
解得
(3)当对应弦长为d时,做匀速圆周运动的时间最短,微粒的运动轨迹如图所示
由几何关系
解得
根据
最短时间
答案第1页,共2页
答案第20页,共1页
