椭圆及其标准方程(第一课时)1
文档属性
| 名称 | 椭圆及其标准方程(第一课时)1 |

|
|
| 格式 | zip | ||
| 文件大小 | 374.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-04 00:00:00 | ||
图片预览




文档简介
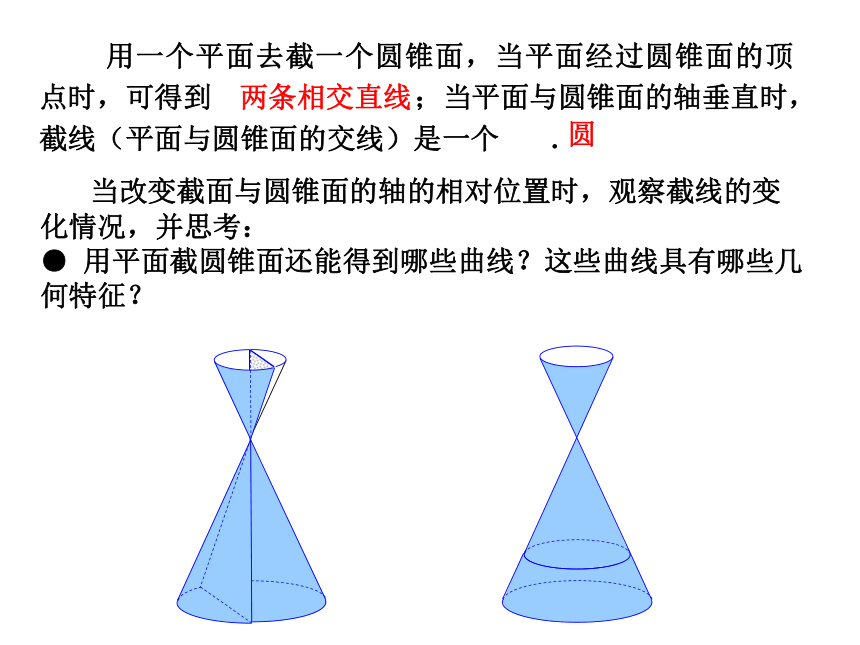
课件19张PPT。第二章 圆锥曲线与方程选修1-1(第1课时) 2.1 椭圆及其标准方程 用一个平面去截一个圆锥面,当平面经过圆锥面的顶点时,可得到 ;当平面与圆锥面的轴垂直时,截线(平面与圆锥面的交线)是一个 .
当改变截面与圆锥面的轴的相对位置时,观察截线的变化情况,并思考:
● 用平面截圆锥面还能得到哪些曲线?这些曲线具有哪些几何特征?
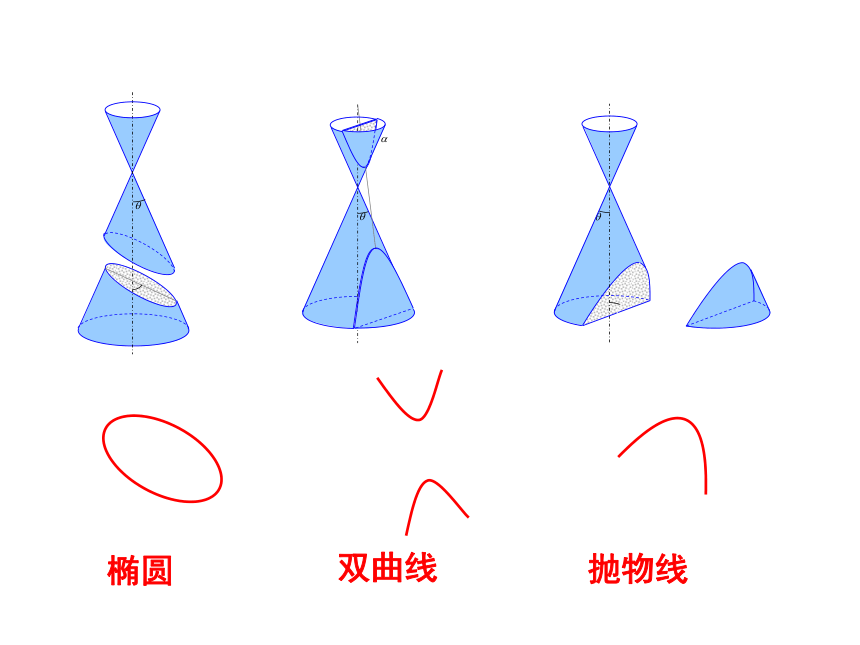
两条相交直线圆
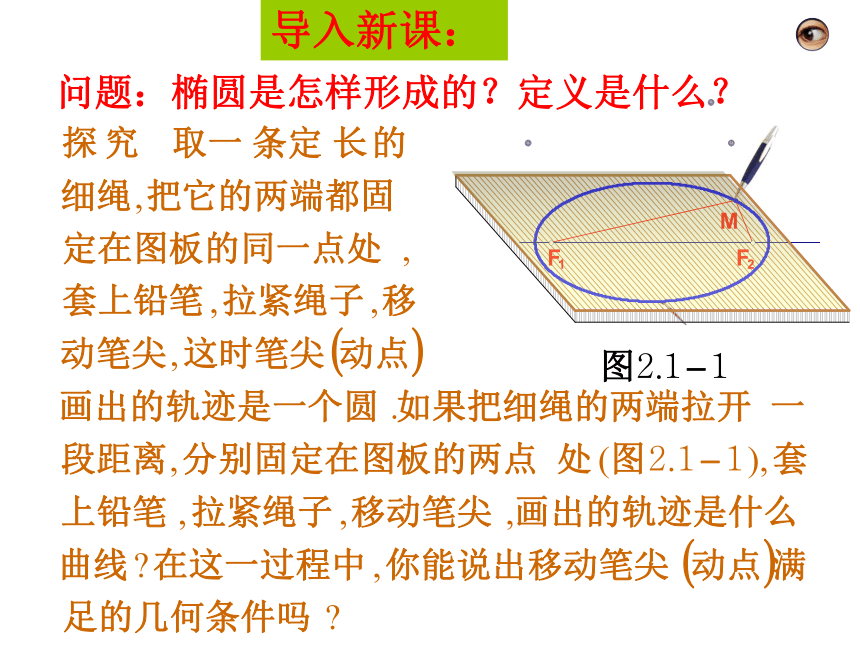
椭圆双曲线抛物线导入新课:问题:椭圆是怎样形成的?定义是什么?椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。几点说明:2、F1、F2是两个不同的定点;3、M是椭圆上任意一点,且|MF1| + |MF2| = 常数;4、通常这个常数记为2a,焦距记为2c,且2a>2c(?);5、如果2a = 2c,则M点的轨迹是线段F1F2.6、如果2a < 2c,则M点的轨迹不存在.(由三角形的性质知)若|F1F2| =0 则M点的轨迹是一个圆 1 、必须在同一平面内;练习.用定义判断下列动点M的轨迹是否为椭圆。(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。(4)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹。因|MF1|+|MF2|=6>|F1F2|=4,故点M的轨迹为椭圆。因|MF1|+|MF2|=4=|F1F2|=4,故点M的轨迹不是椭圆
(是线段F1F2)。(3)到F1(0,-2)、F2(0,2)的距离之和为3的点的轨迹。因|MF1|+|MF2|=4<|F1F2|=4,故点M的轨迹不存在。xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设|F1F2|=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足|PF1 | + | PF2 |
为定值,设为2a,则2a>2cO是椭圆的标准方程. 若以F1,F2所在的直线为y轴,
线段 F1F2的垂直平分线为x 轴建立
直角坐标系,推导出的方程又是怎
样的呢?也是椭圆的标准方程.注:椭圆的焦点在坐标轴上,且两焦
点的中点为坐标原点.椭圆标准方程的推导方
程
特
点(2)在椭圆两种标准方程中,总有a>b>0;(4)a、b、c都有特定的意义:a—椭圆上任意一点P到F1、F2距离和的一半;c—半焦距.有关系式 成立。椭圆的标准方程(3)焦点在大分母变量所对应的那个轴上(焦点跟着大的跑);(1)方程的左边是两项平方和的形式,等号的右边是1;(5) RtΔPOF2是特征三角形。分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹根据所学知识完成下表练习1:写出适合下列条件的椭圆标准方程:巩固应用练习2:ADD教材例1. 已知椭圆两焦点的坐标分别是答案:B课堂小结:1、椭圆的定义 2、椭圆的标准方程
当改变截面与圆锥面的轴的相对位置时,观察截线的变化情况,并思考:
● 用平面截圆锥面还能得到哪些曲线?这些曲线具有哪些几何特征?
两条相交直线圆
椭圆双曲线抛物线导入新课:问题:椭圆是怎样形成的?定义是什么?椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。几点说明:2、F1、F2是两个不同的定点;3、M是椭圆上任意一点,且|MF1| + |MF2| = 常数;4、通常这个常数记为2a,焦距记为2c,且2a>2c(?);5、如果2a = 2c,则M点的轨迹是线段F1F2.6、如果2a < 2c,则M点的轨迹不存在.(由三角形的性质知)若|F1F2| =0 则M点的轨迹是一个圆 1 、必须在同一平面内;练习.用定义判断下列动点M的轨迹是否为椭圆。(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。(4)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹。因|MF1|+|MF2|=6>|F1F2|=4,故点M的轨迹为椭圆。因|MF1|+|MF2|=4=|F1F2|=4,故点M的轨迹不是椭圆
(是线段F1F2)。(3)到F1(0,-2)、F2(0,2)的距离之和为3的点的轨迹。因|MF1|+|MF2|=4<|F1F2|=4,故点M的轨迹不存在。xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设|F1F2|=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足|PF1 | + | PF2 |
为定值,设为2a,则2a>2cO是椭圆的标准方程. 若以F1,F2所在的直线为y轴,
线段 F1F2的垂直平分线为x 轴建立
直角坐标系,推导出的方程又是怎
样的呢?也是椭圆的标准方程.注:椭圆的焦点在坐标轴上,且两焦
点的中点为坐标原点.椭圆标准方程的推导方
程
特
点(2)在椭圆两种标准方程中,总有a>b>0;(4)a、b、c都有特定的意义:a—椭圆上任意一点P到F1、F2距离和的一半;c—半焦距.有关系式 成立。椭圆的标准方程(3)焦点在大分母变量所对应的那个轴上(焦点跟着大的跑);(1)方程的左边是两项平方和的形式,等号的右边是1;(5) RtΔPOF2是特征三角形。分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹根据所学知识完成下表练习1:写出适合下列条件的椭圆标准方程:巩固应用练习2:ADD教材例1. 已知椭圆两焦点的坐标分别是答案:B课堂小结:1、椭圆的定义 2、椭圆的标准方程
