2-1,1椭圆及其标准方程(第二课时)
文档属性
| 名称 | 2-1,1椭圆及其标准方程(第二课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 443.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-04 00:00:00 | ||
图片预览





文档简介
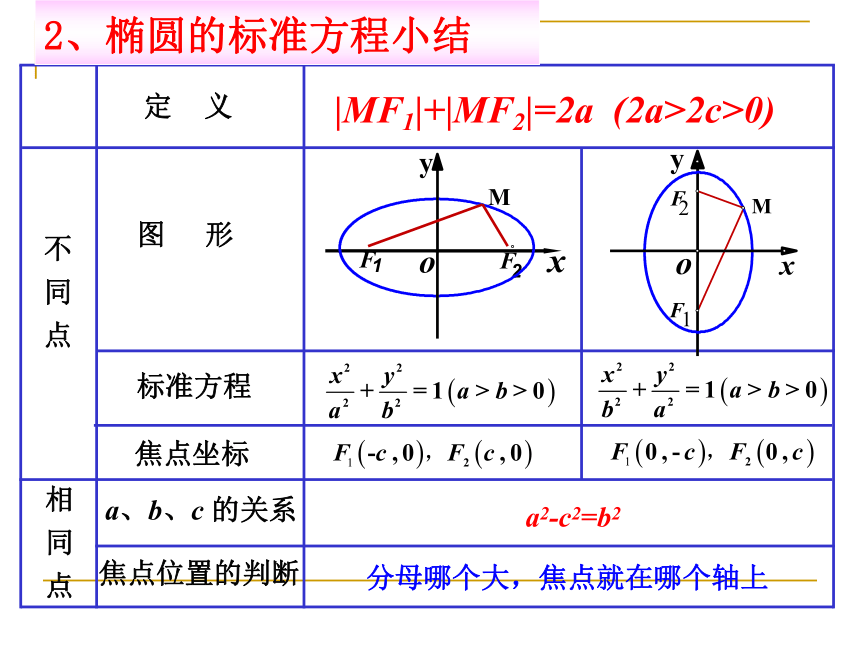
课件13张PPT。第二章 圆锥曲线与方程
§2.1.1 椭圆及其标准方程第 二 课 时1、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的动点M的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距|F1F2|=2c 。几点说明:1、椭圆定义式:|MF1| + |MF2| = 2a > |F1F2|=2c.则M点的轨迹是椭圆.2、若|MF1| + |MF2| = 2a = |F1F2|=2c ,则M点的轨迹是线段F1F2.3、若|MF1| + |MF2| = 2a < |F1F2|=2c ,则M点的轨迹不存在.复习回顾分母哪个大,焦点就在哪个轴上a2-c2=b22、椭圆的标准方程小结|MF1|+|MF2|=2a (2a>2c>0)例1.椭圆的两个焦点的坐标分别是(-4,0)
(4,0),椭圆上一点P到两焦点距离之和等于10,
求椭圆的标准方程。 解: ∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为
变式:求适合下列条件的椭圆的标准方程:
(1)焦点在y轴上,且经过两个点(0,2)和(1,0). [一点通] 用待定系数法求椭圆的标准方程,一般解题步骤可归纳为1、建系 2、设标 3、列式 4、化简 5、检验(可省略不写)例3、如图,设点A,B的坐标分别为(-5,0),(5,0)。
直线AM,BM相交于点M,且它们的斜率之积是
,求点M的轨迹方程。解:设点M的坐标为(x,y),因为点A的坐标是,所以直线
AM的斜率同理,直线BM的斜率由已知有化简,得点M的轨迹方程为课后练习: 1 化简方程:答案:B
§2.1.1 椭圆及其标准方程第 二 课 时1、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的动点M的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距|F1F2|=2c 。几点说明:1、椭圆定义式:|MF1| + |MF2| = 2a > |F1F2|=2c.则M点的轨迹是椭圆.2、若|MF1| + |MF2| = 2a = |F1F2|=2c ,则M点的轨迹是线段F1F2.3、若|MF1| + |MF2| = 2a < |F1F2|=2c ,则M点的轨迹不存在.复习回顾分母哪个大,焦点就在哪个轴上a2-c2=b22、椭圆的标准方程小结|MF1|+|MF2|=2a (2a>2c>0)例1.椭圆的两个焦点的坐标分别是(-4,0)
(4,0),椭圆上一点P到两焦点距离之和等于10,
求椭圆的标准方程。 解: ∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为
变式:求适合下列条件的椭圆的标准方程:
(1)焦点在y轴上,且经过两个点(0,2)和(1,0). [一点通] 用待定系数法求椭圆的标准方程,一般解题步骤可归纳为1、建系 2、设标 3、列式 4、化简 5、检验(可省略不写)例3、如图,设点A,B的坐标分别为(-5,0),(5,0)。
直线AM,BM相交于点M,且它们的斜率之积是
,求点M的轨迹方程。解:设点M的坐标为(x,y),因为点A的坐标是,所以直线
AM的斜率同理,直线BM的斜率由已知有化简,得点M的轨迹方程为课后练习: 1 化简方程:答案:B
