第1章1.1.2余弦定理 (第二课时)
文档属性
| 名称 | 第1章1.1.2余弦定理 (第二课时) |  | |
| 格式 | zip | ||
| 文件大小 | 594.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-04 21:49:38 | ||
图片预览





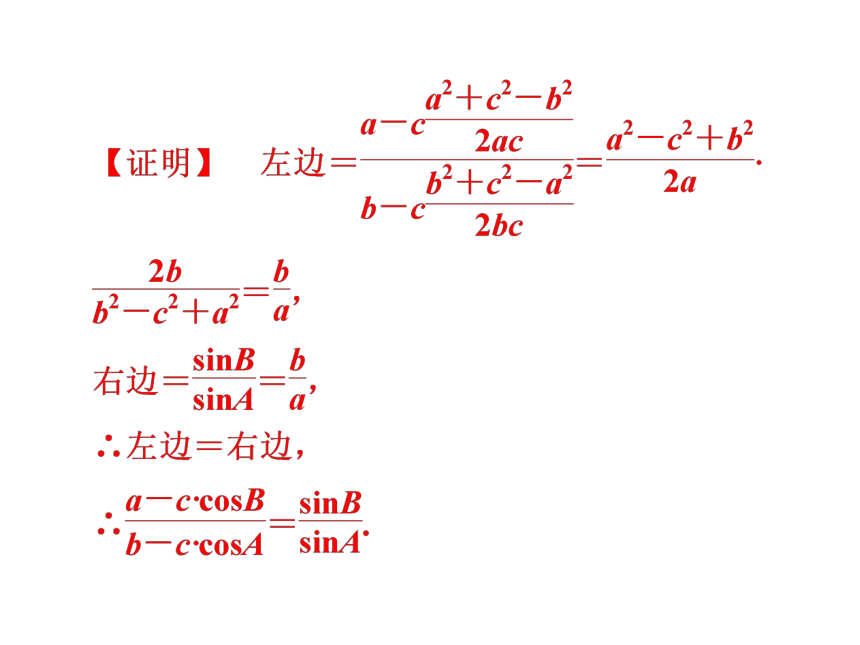

文档简介
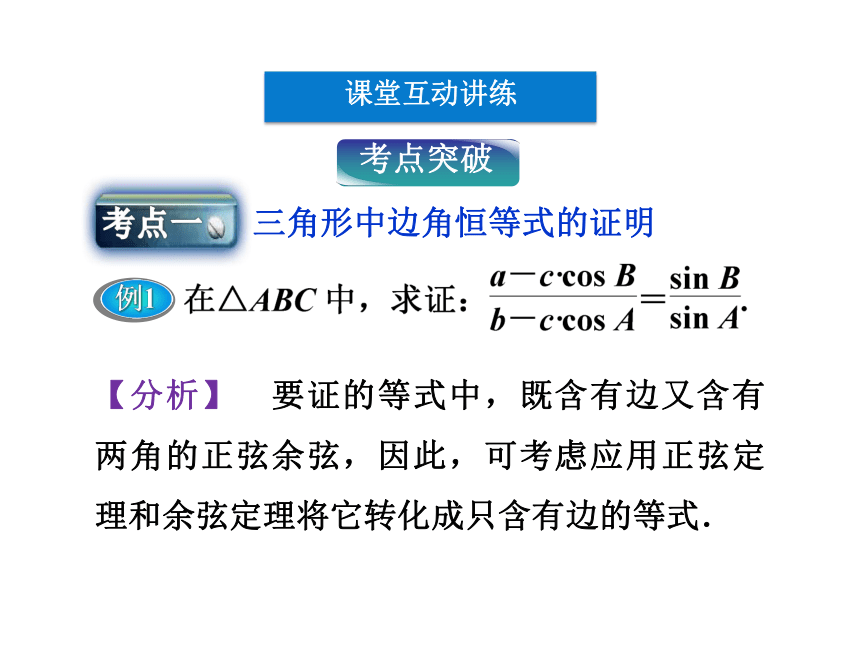
课件26张PPT。第二课时 课堂互动讲练知能优化训练第二课时课前自主学案课前自主学案1.余弦定理:__________________,_________
__________,__________________.
2.利用余弦定理可解决两类问题:
(1)已知三边,求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角.a2=b2+c2-2bccosAc2=a2+b2-2abcosC1.判断三角形的形状
(1)判断三角形的形状是看该三角形是否为某些特殊的三角形(如锐角、直角、钝角、等腰、等边三角形等);
(2)对于给出条件是边角关系混合在一起的问题,一般地,应运用正弦定理和余弦定理,要么把它统一为边的关系;要么统一为角的关系.再利用三角形的有关知识,三角恒等变形方法、代数恒等变形方法进行转化、化简,从而得出结论.a2+b2=c2a2+b2>c2a2+b2在△ABC中,a2+b2>c2,那么△ABC是锐角三角形吗?
提示:不一定,因为由a2+b2>c2只能说明C为锐角,不能说明A、B也为锐角.
2.余弦定理与三角函数的综合问题课堂互动讲练【分析】 要证的等式中,既含有边又含有两角的正弦余弦,因此,可考虑应用正弦定理和余弦定理将它转化成只含有边的等式.自我挑战1 在△ABC中,D为BC的中点,求证:2(AD2+BD2)=AB2+AC2.证明:如图,延长AD至E,使AD=DE,连结BE,CE,则四边形ABEC是平
行四边形.由余弦定理,得
BC2=AB2+AC2-2AB·AC·
cos∠BAC, ①AE2=BA2+BE2-2BA·BE·cos∠ABE, ②
①+②得:BC2+AE2=2AB2+AC2+BE2-2AB·AC·cos∠BAC-2BA·BE·cos∠ABE.又因为∠ABE+∠BAC=π,BC=2BD,AE=2AD. AC=BE,所以4(BD2+AD2)=2AB2+2AC2-2AB·AC·cos∠BAC+2BA·AC·cos∠BAC,即2(BD2+AD2)=AB2+AC2. 在△ABC中,若b2sin2C+c2sin2B=2bccosBcosC,试判断三角形的形状.
【分析】 判断三角形的形状通常从三角形内角的关系来确定,也可以从三边关系来确定.【点评】 利用正弦定理、余弦定理可以实现边角关系的互化.自我挑战2 △ABC中,已知a-b=c·(cosB-cosA),试判断△ABC的形状.所以0=(a-b)[(b+a)2-c2-2ab]=(a-b)(a2+b2-c2),所以a-b=0或a2+b2-c2=0,
所以△ABC是等腰三角形或直角三角形.
法二:(边化角)由正弦定理,得sinA-sinB=sinC(cosB-cosA)=sin(A+B)(cosB-cosA)=(sinAcosB+cosAsinB)·(cosB-cosA)=sinAcos2B-sinAcosAcosB+cosAsinBcosB-sinBcos2A,
所以sinA(1-cos2B)=-sinAcosAcosB+cosAsinBcosB+sinB(1-cos2A),
即sinAsin2B=-sinAcosAcosB+cosAsinBcosB+sinBsin2A,【分析】 利用二倍角公式及诱导公式求出C角,结合余弦定理可求出b值.【点评】 熟练应用三角公式化简求角,再结合面积公式及正余弦定理是解决此类综合题的关键,但要注意解关于边或角的方程时根的检验.1.正弦定理和余弦定理的每一个等式中都包含三角形的四个元素,如果其中三个元素是已知的(其中至少有一个元素是边),那么这个三角形一定可解.
2.正弦定理和余弦定理的特殊功能是边角互换,即利用它们可以把边的关系转化为角的关系,也可以把角的关系转化为边的关系,从而使许多问题得以解决.3.判断三角形的形状,一般考虑从两个方向进行变形,一个方向是边,走代数变形之路,通常正、余弦定理结合使用;另一个方向是角,走三角变形之路,通常是运用正弦定理,要注重边角转化桥梁——正、余弦定理.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
__________,__________________.
2.利用余弦定理可解决两类问题:
(1)已知三边,求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角.a2=b2+c2-2bccosAc2=a2+b2-2abcosC1.判断三角形的形状
(1)判断三角形的形状是看该三角形是否为某些特殊的三角形(如锐角、直角、钝角、等腰、等边三角形等);
(2)对于给出条件是边角关系混合在一起的问题,一般地,应运用正弦定理和余弦定理,要么把它统一为边的关系;要么统一为角的关系.再利用三角形的有关知识,三角恒等变形方法、代数恒等变形方法进行转化、化简,从而得出结论.a2+b2=c2a2+b2>c2a2+b2
提示:不一定,因为由a2+b2>c2只能说明C为锐角,不能说明A、B也为锐角.
2.余弦定理与三角函数的综合问题课堂互动讲练【分析】 要证的等式中,既含有边又含有两角的正弦余弦,因此,可考虑应用正弦定理和余弦定理将它转化成只含有边的等式.自我挑战1 在△ABC中,D为BC的中点,求证:2(AD2+BD2)=AB2+AC2.证明:如图,延长AD至E,使AD=DE,连结BE,CE,则四边形ABEC是平
行四边形.由余弦定理,得
BC2=AB2+AC2-2AB·AC·
cos∠BAC, ①AE2=BA2+BE2-2BA·BE·cos∠ABE, ②
①+②得:BC2+AE2=2AB2+AC2+BE2-2AB·AC·cos∠BAC-2BA·BE·cos∠ABE.又因为∠ABE+∠BAC=π,BC=2BD,AE=2AD. AC=BE,所以4(BD2+AD2)=2AB2+2AC2-2AB·AC·cos∠BAC+2BA·AC·cos∠BAC,即2(BD2+AD2)=AB2+AC2. 在△ABC中,若b2sin2C+c2sin2B=2bccosBcosC,试判断三角形的形状.
【分析】 判断三角形的形状通常从三角形内角的关系来确定,也可以从三边关系来确定.【点评】 利用正弦定理、余弦定理可以实现边角关系的互化.自我挑战2 △ABC中,已知a-b=c·(cosB-cosA),试判断△ABC的形状.所以0=(a-b)[(b+a)2-c2-2ab]=(a-b)(a2+b2-c2),所以a-b=0或a2+b2-c2=0,
所以△ABC是等腰三角形或直角三角形.
法二:(边化角)由正弦定理,得sinA-sinB=sinC(cosB-cosA)=sin(A+B)(cosB-cosA)=(sinAcosB+cosAsinB)·(cosB-cosA)=sinAcos2B-sinAcosAcosB+cosAsinBcosB-sinBcos2A,
所以sinA(1-cos2B)=-sinAcosAcosB+cosAsinBcosB+sinB(1-cos2A),
即sinAsin2B=-sinAcosAcosB+cosAsinBcosB+sinBsin2A,【分析】 利用二倍角公式及诱导公式求出C角,结合余弦定理可求出b值.【点评】 熟练应用三角公式化简求角,再结合面积公式及正余弦定理是解决此类综合题的关键,但要注意解关于边或角的方程时根的检验.1.正弦定理和余弦定理的每一个等式中都包含三角形的四个元素,如果其中三个元素是已知的(其中至少有一个元素是边),那么这个三角形一定可解.
2.正弦定理和余弦定理的特殊功能是边角互换,即利用它们可以把边的关系转化为角的关系,也可以把角的关系转化为边的关系,从而使许多问题得以解决.3.判断三角形的形状,一般考虑从两个方向进行变形,一个方向是边,走代数变形之路,通常正、余弦定理结合使用;另一个方向是角,走三角变形之路,通常是运用正弦定理,要注重边角转化桥梁——正、余弦定理.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
