1.2 正弦定理、余弦定理的应用举例
文档属性
| 名称 | 1.2 正弦定理、余弦定理的应用举例 |  | |
| 格式 | zip | ||
| 文件大小 | 842.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-04 21:50:52 | ||
图片预览








文档简介
课件36张PPT。1.2 应用举例学习目标
1.运用正弦定理、余弦定理等知识解决一些与测量和几何计算有关的实际问题.
2.通过对实际问题的探索,会利用数学建模思想把实际问题转化为数学问题,增强解决实际问题的能力,培养数学应用意识. 课堂互动讲练知能优化训练1.2
应
用
举
例课前自主学案课前自主学案a2=b2+c2-2bccosAb2=a2+c2-2accosBc2=a2+b2-2abcosC1.关于解斜三角形应用题的步骤
(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如坡度、仰角、俯角、视角、象限角、方位角、方向角等;
(2)概据题意画出图形;(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要算法简练,计算准确,最后作答.
2.解斜三角形的实际应用题的典型问题
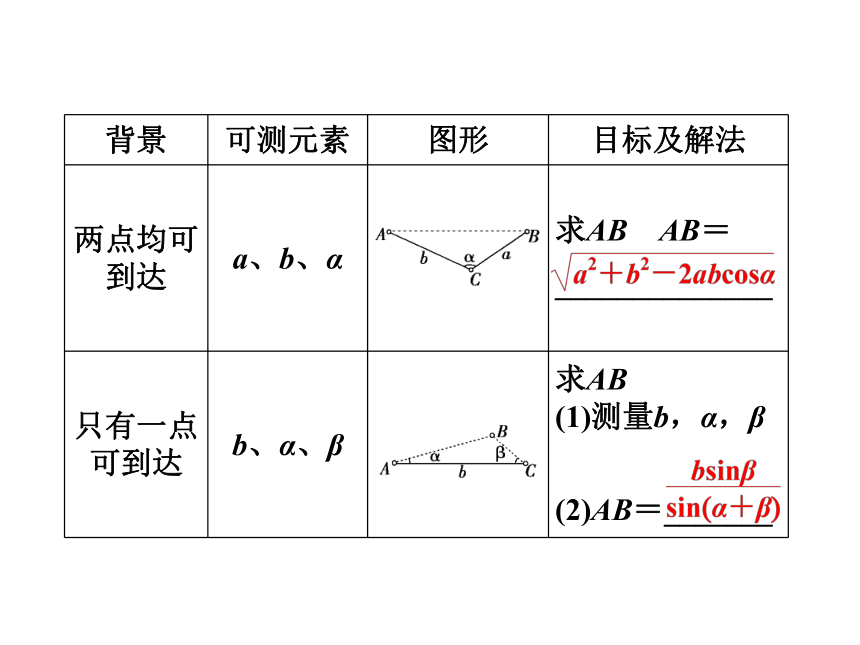
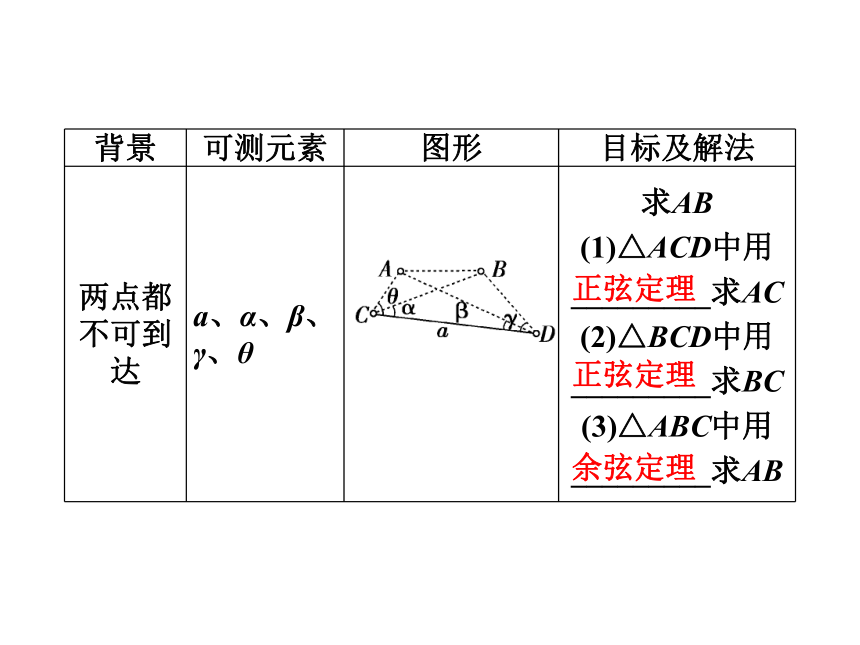
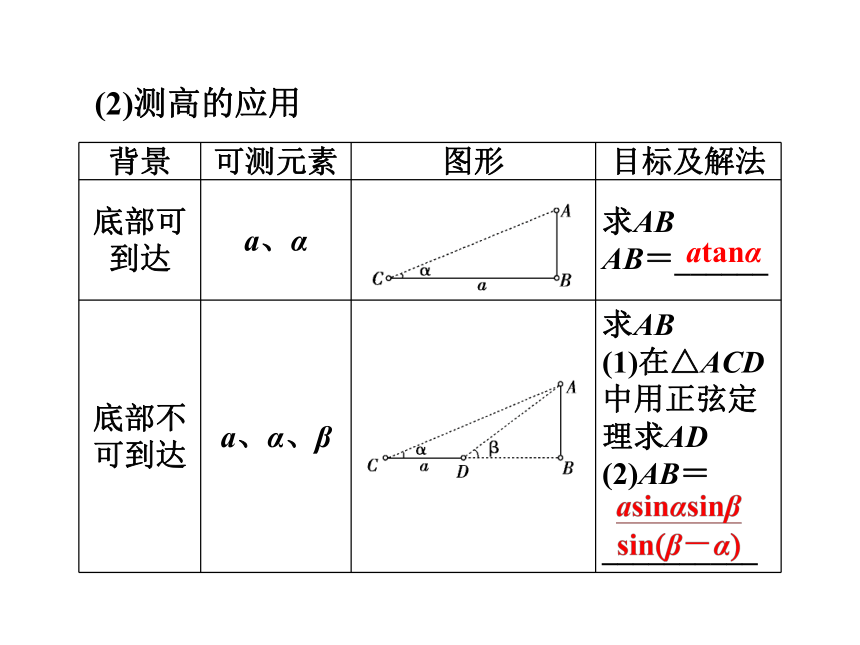
(1)测距离的应用正弦定理正弦定理余弦定理(2)测高的应用atanα(3)机械制造:自动装卸车、曲柄连杆
(4)角度问题:如航海问题课堂互动讲练测量不可到达的两点的距离时,若是其中一点可以到达,利用一个三角形即可解决,一般用正弦定理;若是两点均不可到达,则需要用两个三角形才能解决,一般正、余弦定理都要用到.(1)A与D间的距离;
(2)灯塔C与D间的距离.【点评】 测量两个不可到达的点之间的距离问题,一般是把求距离问题转化为求三角形的边长问题.首先是明确题意,根据条件和图形特点寻找可解的三角形,然后利用正弦定理或余弦定理求解(另外基线的选取要恰当).自我挑战1 一人见一建筑物A在正北方向,另一建筑物B在北偏西30°方向,此人向北偏西70°方向行走3 km后,则见A在其北偏东56°方向,B在其北偏东74°方向,试求这两个建筑物的距离.(精确到10 m) 如图,当甲船位于A处时获
悉,在其正东方向相距20海里
的B处有一艘船遇险等待营救,
甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援?(角度精确到1°)【分析】 △ABC中,利用正弦定理可求得BC,再利用余弦定理可求得∠ACB.【点评】 注意确定方位角的大小,关键是弄清正东、南偏西、北偏东这些方位角的概念. 如图所示,在地面上有一旗杆
OP,为测得它的高度h,在地面上
取一线段AB,AB=20 m,在A处
测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,又测得∠AOB=60°.求旗杆的高度.【分析】 设出旗杆的高度为h,△AOP与△BOP都为直角三角形,可用h表示出OA与OB,在△AOB中,用余弦定理列式即可求解.【点评】 题目中出现多个三角形,应注意根据已知条件找出角度的关系,通过已知量表示出未知量,化归到一个三角形中利用正、余弦定理解决.自我挑战3 为了测量建造中的某城市电视塔已达到的高度,小明在学校操场的某一条直线上选择A、B、C三点,且AB=BC=60 m,在A,B,C三点观察塔的最高点,测得的仰角分别为45°,54.2°,60°,小明的身高为1.5 m,试求建造中的电视塔现在已达到的高度.(结果保留1位小数)1.利用数学建模的思想结合三角形有关知识解应用题的步骤:
(1)根据题意作示意图;
(2)抽象概括出数学模型;
(3)用正、余弦定理解决数学模型;
(4)检验所得解,得到实际问题的解.2.在选择关系式时,一是要力求简便;二是尽可能使用题中原有的已知数据,尽量减少计算中误差的积累,实际应用题的结果若是近似值要按照题目的具体要求和常规要求计算与保留,并注明单位.
3.注意专业术语的含义,如:仰角、俯角、方位角、倾斜角、铅直平面等.
4.解应用题关键是将文字语言翻译成数学语言,进而抽象成数学问题,常用方法有列表、画图等技巧,并注意解完后的验证.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
1.运用正弦定理、余弦定理等知识解决一些与测量和几何计算有关的实际问题.
2.通过对实际问题的探索,会利用数学建模思想把实际问题转化为数学问题,增强解决实际问题的能力,培养数学应用意识. 课堂互动讲练知能优化训练1.2
应
用
举
例课前自主学案课前自主学案a2=b2+c2-2bccosAb2=a2+c2-2accosBc2=a2+b2-2abcosC1.关于解斜三角形应用题的步骤
(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如坡度、仰角、俯角、视角、象限角、方位角、方向角等;
(2)概据题意画出图形;(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要算法简练,计算准确,最后作答.
2.解斜三角形的实际应用题的典型问题
(1)测距离的应用正弦定理正弦定理余弦定理(2)测高的应用atanα(3)机械制造:自动装卸车、曲柄连杆
(4)角度问题:如航海问题课堂互动讲练测量不可到达的两点的距离时,若是其中一点可以到达,利用一个三角形即可解决,一般用正弦定理;若是两点均不可到达,则需要用两个三角形才能解决,一般正、余弦定理都要用到.(1)A与D间的距离;
(2)灯塔C与D间的距离.【点评】 测量两个不可到达的点之间的距离问题,一般是把求距离问题转化为求三角形的边长问题.首先是明确题意,根据条件和图形特点寻找可解的三角形,然后利用正弦定理或余弦定理求解(另外基线的选取要恰当).自我挑战1 一人见一建筑物A在正北方向,另一建筑物B在北偏西30°方向,此人向北偏西70°方向行走3 km后,则见A在其北偏东56°方向,B在其北偏东74°方向,试求这两个建筑物的距离.(精确到10 m) 如图,当甲船位于A处时获
悉,在其正东方向相距20海里
的B处有一艘船遇险等待营救,
甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援?(角度精确到1°)【分析】 △ABC中,利用正弦定理可求得BC,再利用余弦定理可求得∠ACB.【点评】 注意确定方位角的大小,关键是弄清正东、南偏西、北偏东这些方位角的概念. 如图所示,在地面上有一旗杆
OP,为测得它的高度h,在地面上
取一线段AB,AB=20 m,在A处
测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,又测得∠AOB=60°.求旗杆的高度.【分析】 设出旗杆的高度为h,△AOP与△BOP都为直角三角形,可用h表示出OA与OB,在△AOB中,用余弦定理列式即可求解.【点评】 题目中出现多个三角形,应注意根据已知条件找出角度的关系,通过已知量表示出未知量,化归到一个三角形中利用正、余弦定理解决.自我挑战3 为了测量建造中的某城市电视塔已达到的高度,小明在学校操场的某一条直线上选择A、B、C三点,且AB=BC=60 m,在A,B,C三点观察塔的最高点,测得的仰角分别为45°,54.2°,60°,小明的身高为1.5 m,试求建造中的电视塔现在已达到的高度.(结果保留1位小数)1.利用数学建模的思想结合三角形有关知识解应用题的步骤:
(1)根据题意作示意图;
(2)抽象概括出数学模型;
(3)用正、余弦定理解决数学模型;
(4)检验所得解,得到实际问题的解.2.在选择关系式时,一是要力求简便;二是尽可能使用题中原有的已知数据,尽量减少计算中误差的积累,实际应用题的结果若是近似值要按照题目的具体要求和常规要求计算与保留,并注明单位.
3.注意专业术语的含义,如:仰角、俯角、方位角、倾斜角、铅直平面等.
4.解应用题关键是将文字语言翻译成数学语言,进而抽象成数学问题,常用方法有列表、画图等技巧,并注意解完后的验证.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
