人教版八年级数学 下册 第十八章 18.2.2 菱形 第1课时 菱形的性质 课件(共33张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 第十八章 18.2.2 菱形 第1课时 菱形的性质 课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 508.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览








文档简介
(共33张PPT)
创设情境 引出课题
平行四边形的性质
矩形的性质
对边相等
对角相等
对角线互相平分
对角线把平行四边
形分成四个面积相
等的三角形。(中心
对称图形)
对边相等
四个角都是直角
对角线互相平分且相等
对角线把矩形分成四个
面积相等的等腰三角形
(中心对称图形,轴对
称图形)
特殊化
平行四边形的角特殊化得到特殊的平行四
边形——矩形;平行四边形的边特殊化,我们
得到的特 殊的平行四边形是什么,它有什么
特征?
创设情境 引出课题
18.2.2 菱 形
人教版八年级数学 下册
第1课时 菱形的性质
学习目标:
1.归纳、探究菱形的概念和性质。
2. 会用菱形的性质解决简单的实际问题。
学习重点:
菱形性质的探索、证明和应用.
思考 如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
菱形
邻边相等
目标导学一:菱形的性质
菱形的定义:有一组邻边相等的平行四边形是菱形
温馨提示:菱形的定义有两个要素:
①四边形是平行四边形
②有一组邻边相等,二者缺一不可。
菱形是特殊的平行四边形,因此它具有平行四边形的所有性质,但它也有自己独特的性质。
A
B
C
D
你能举出生活中的菱形的实际例子吗?
追问:你能画出一个菱形吗?
活动 在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:
猜想1 菱形的四条边都相等.
猜想2 菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
问题1 菱形是轴对称图形吗 如果是,指出它的对称轴.
是,两条对角线所在直线都是它的对称轴.
问题2 根据上面折叠过程,猜想菱形的四边在数量上
有什么关系 菱形的两对角线有什么关系
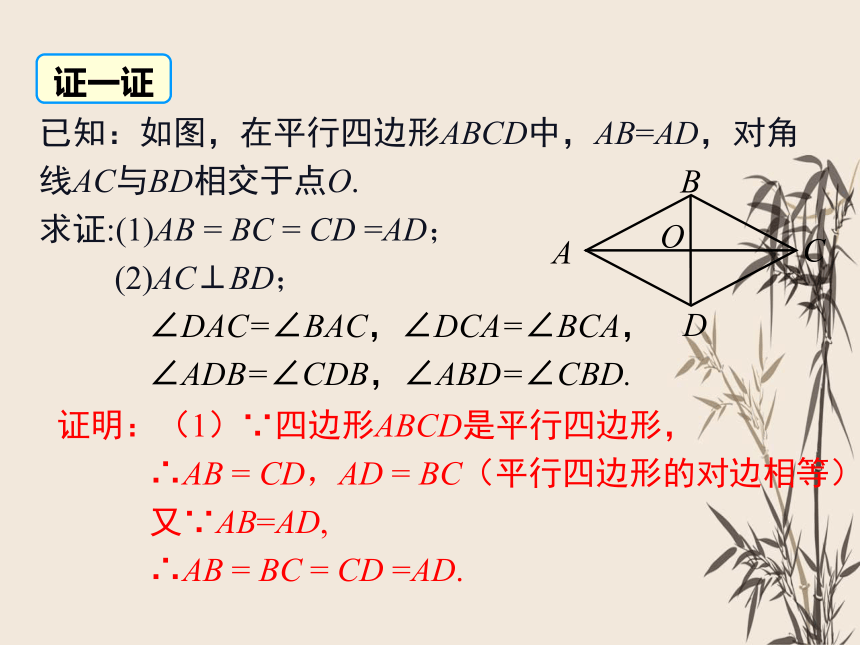
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
证明:(1)∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边相等).
又∵AB=AD,
∴AB = BC = CD =AD.
A
B
C
O
D
证一证
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是平行四边形,
∴OB = OD (平行四边形的对角线互相平分).
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
A
B
C
O
D
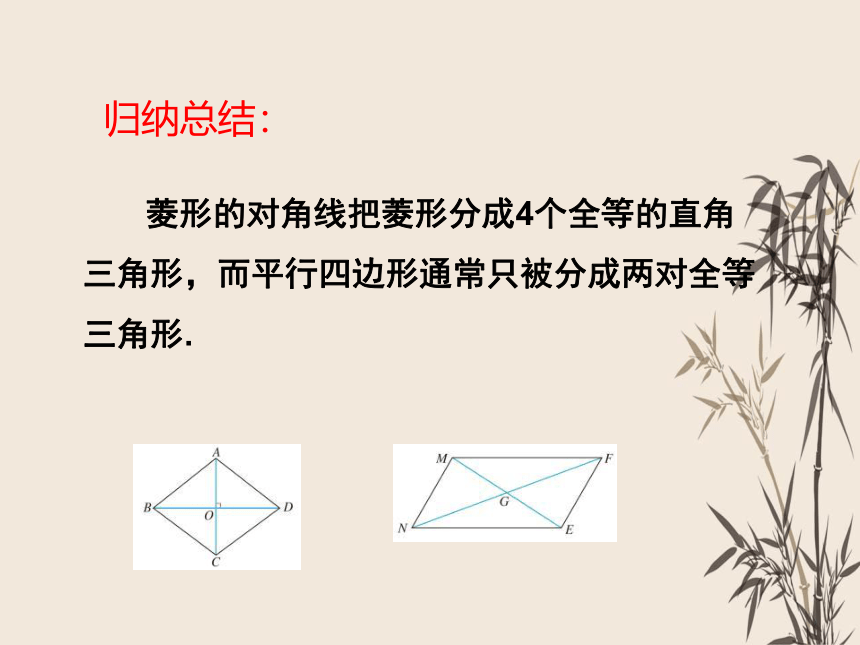
归纳总结:
菱形的对角线把菱形分成4个全等的直角三角形,而平行四边形通常只被分成两对全等三角形.
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂
直平分,并且每一
条对角线平分一组
对角
平行四边形的性质
矩形的性质
菱形的性质
对边相等
对角相等
对角线互相平分
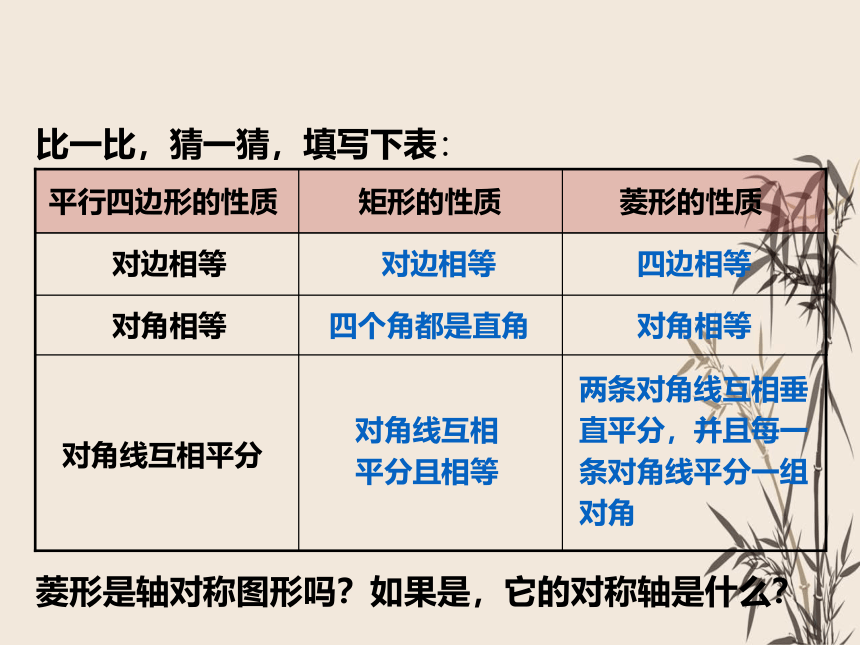
比一比,猜一猜,填写下表:
菱形是轴对称图形吗?如果是,它的对称轴是什么?
对称性:菱形既是轴对称图形,又是中心对称图形,有两条对称轴,其对称轴为两条对角线所在直线,对称中心为其对角线的交点。
例1 如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,
AO= AC,BO= BD.
∵AC=6cm,BD=12cm,
∴AO=3cm,BO=6cm.
在Rt△ABO中,由勾股定理得
∴菱形的周长=4AB=4×3 =12 (cm).
精典例题
例2 如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,
即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.
∴AE=AF.
菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
规律
例3 如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
A
B
C
D
O
E
证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA,
∠ABC=∠ADC=2∠ADB ,
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB,
∴∠ABC=∠DAE,
∵∠DAE=2∠BAE,∴∠BAE=∠ADB.
又∵AD=BA ,
∴△AOD≌△BEA ,
∴AO=BE .
1.如图,在菱形ABCD中,已知∠A=60°,AB=
5,则△ABD的周长是 ( )
A.10 B.12 C.15 D.20
C
2.如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
第1题图
第2题图
6cm
即学即练
思考:菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗
A
B
C
D
猜想:前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高
=BC·AE.
E
目标导学二:菱形的面积
如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
你有什么发现?
菱形的面积 = 底×高 = 对角线乘积的一半
合作探究
例4 如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h= .
菱形的面积:
(1)面积=底×高
(2)面积=两条对角线的长的乘积的一半
S菱形ABCD= AC · BD
方法归纳
例5 如图,菱形花坛ABCD的边长为20m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.
求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
精典例题
解:∵花坛ABCD是 ,
∴AC⊥ ,
∠ABO= = ∠ __ = × = .
在Rt△OAB中,AO= = × = ,
(菱形的两条对角线_______________)
BO= = = .
∴花坛的两条小路长 AC=2AO= ,
BD=2BO=____≈__ .
花坛的面积 =4× __
= ·____=_________≈ .
菱形
BD
∠CBO
ABC
60°
30°
AB
20
10
互相垂直平分
20(m)
BD
AC
34.64(m)
346.4(m2)
菱形的两条对角线的长的比为3∶4,面积为24cm2,求菱形的周长.
解:设一条对角线长为3x,则另一条对角线长为4x,
S= ×3x·4x=24,∴x=2.
边长= =5.
∴菱形的周长=4×5=20(cm).
拓展提升
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
比较探究
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结
1.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A. 1 B.2 C. 3 D. 4
B
检测目标
2.如图,已知菱形的两条对角线长分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm
C.5cm D.9.6cm
B
检测目标
3.菱形具有而平行四边形不具有的性质是( )
A 对角线互相平分
B 对角线相等
C 对角线互相垂直且相等
D 对角线互相垂直,每一条对角线平分一组对角
D
检测目标
4.四边形ABCD是菱形,对角线AC、BD相交于点O,且AB=5,AO=4.求AC和BD的长.
O
解:如图所示
由菱形的性质可得:
AC=2 AO=2×4=8
在Rt△OAB中,
即:BD=2BO=2×3=6
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
创设情境 引出课题
平行四边形的性质
矩形的性质
对边相等
对角相等
对角线互相平分
对角线把平行四边
形分成四个面积相
等的三角形。(中心
对称图形)
对边相等
四个角都是直角
对角线互相平分且相等
对角线把矩形分成四个
面积相等的等腰三角形
(中心对称图形,轴对
称图形)
特殊化
平行四边形的角特殊化得到特殊的平行四
边形——矩形;平行四边形的边特殊化,我们
得到的特 殊的平行四边形是什么,它有什么
特征?
创设情境 引出课题
18.2.2 菱 形
人教版八年级数学 下册
第1课时 菱形的性质
学习目标:
1.归纳、探究菱形的概念和性质。
2. 会用菱形的性质解决简单的实际问题。
学习重点:
菱形性质的探索、证明和应用.
思考 如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
菱形
邻边相等
目标导学一:菱形的性质
菱形的定义:有一组邻边相等的平行四边形是菱形
温馨提示:菱形的定义有两个要素:
①四边形是平行四边形
②有一组邻边相等,二者缺一不可。
菱形是特殊的平行四边形,因此它具有平行四边形的所有性质,但它也有自己独特的性质。
A
B
C
D
你能举出生活中的菱形的实际例子吗?
追问:你能画出一个菱形吗?
活动 在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:
猜想1 菱形的四条边都相等.
猜想2 菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
问题1 菱形是轴对称图形吗 如果是,指出它的对称轴.
是,两条对角线所在直线都是它的对称轴.
问题2 根据上面折叠过程,猜想菱形的四边在数量上
有什么关系 菱形的两对角线有什么关系
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
证明:(1)∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边相等).
又∵AB=AD,
∴AB = BC = CD =AD.
A
B
C
O
D
证一证
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是平行四边形,
∴OB = OD (平行四边形的对角线互相平分).
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
A
B
C
O
D
归纳总结:
菱形的对角线把菱形分成4个全等的直角三角形,而平行四边形通常只被分成两对全等三角形.
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂
直平分,并且每一
条对角线平分一组
对角
平行四边形的性质
矩形的性质
菱形的性质
对边相等
对角相等
对角线互相平分
比一比,猜一猜,填写下表:
菱形是轴对称图形吗?如果是,它的对称轴是什么?
对称性:菱形既是轴对称图形,又是中心对称图形,有两条对称轴,其对称轴为两条对角线所在直线,对称中心为其对角线的交点。
例1 如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,
AO= AC,BO= BD.
∵AC=6cm,BD=12cm,
∴AO=3cm,BO=6cm.
在Rt△ABO中,由勾股定理得
∴菱形的周长=4AB=4×3 =12 (cm).
精典例题
例2 如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,
即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.
∴AE=AF.
菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
规律
例3 如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
A
B
C
D
O
E
证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA,
∠ABC=∠ADC=2∠ADB ,
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB,
∴∠ABC=∠DAE,
∵∠DAE=2∠BAE,∴∠BAE=∠ADB.
又∵AD=BA ,
∴△AOD≌△BEA ,
∴AO=BE .
1.如图,在菱形ABCD中,已知∠A=60°,AB=
5,则△ABD的周长是 ( )
A.10 B.12 C.15 D.20
C
2.如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
第1题图
第2题图
6cm
即学即练
思考:菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗
A
B
C
D
猜想:前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高
=BC·AE.
E
目标导学二:菱形的面积
如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
你有什么发现?
菱形的面积 = 底×高 = 对角线乘积的一半
合作探究
例4 如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h= .
菱形的面积:
(1)面积=底×高
(2)面积=两条对角线的长的乘积的一半
S菱形ABCD= AC · BD
方法归纳
例5 如图,菱形花坛ABCD的边长为20m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.
求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
精典例题
解:∵花坛ABCD是 ,
∴AC⊥ ,
∠ABO= = ∠ __ = × = .
在Rt△OAB中,AO= = × = ,
(菱形的两条对角线_______________)
BO= = = .
∴花坛的两条小路长 AC=2AO= ,
BD=2BO=____≈__ .
花坛的面积 =4× __
= ·____=_________≈ .
菱形
BD
∠CBO
ABC
60°
30°
AB
20
10
互相垂直平分
20(m)
BD
AC
34.64(m)
346.4(m2)
菱形的两条对角线的长的比为3∶4,面积为24cm2,求菱形的周长.
解:设一条对角线长为3x,则另一条对角线长为4x,
S= ×3x·4x=24,∴x=2.
边长= =5.
∴菱形的周长=4×5=20(cm).
拓展提升
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
比较探究
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结
1.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A. 1 B.2 C. 3 D. 4
B
检测目标
2.如图,已知菱形的两条对角线长分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm
C.5cm D.9.6cm
B
检测目标
3.菱形具有而平行四边形不具有的性质是( )
A 对角线互相平分
B 对角线相等
C 对角线互相垂直且相等
D 对角线互相垂直,每一条对角线平分一组对角
D
检测目标
4.四边形ABCD是菱形,对角线AC、BD相交于点O,且AB=5,AO=4.求AC和BD的长.
O
解:如图所示
由菱形的性质可得:
AC=2 AO=2×4=8
在Rt△OAB中,
即:BD=2BO=2×3=6
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
