2021-2022学年鲁教版(五四制)八年级数学下册6.1菱形的性质与判定基础练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.1菱形的性质与判定基础练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 245.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 21:08:08 | ||
图片预览


文档简介
6.1菱形的性质与判定第一课时菱形的性质基础练
一.选择题(共10小题)
1.若菱形的两条对角线长分别为10和24,则菱形的面积为( )
A.13 B.26 C.120 D.240
2.若菱形的边长为2,则周长是( )
A.2 B.4 C.8 D.16
3.菱形的一个性质是( )
A.四个角相等 B.四条边相等 C.对角线相等 D.对角互补
4.已知菱形ABCD中,∠D=150°,连接AC,则∠BAC等于( )
A.10° B.15° C.20° D.25°
5.下列说法中不正确的是( )
A.平行四边形的对角相等
B.菱形的邻边相等
C.菱形的对角线互相垂直且相等
D.平行四边形的对角线互相平分
6.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
7.如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
8.菱形的面积为12cm2,一条对角线是6cm,那么菱形的另一条对角线长为( )
A.3cm B.4cm C.5cm D.6cm
9.如图,菱形ABCD中,AC=6,BD=8,AH⊥BC于点H,则AH=( )
A.24 B.10 C. D.
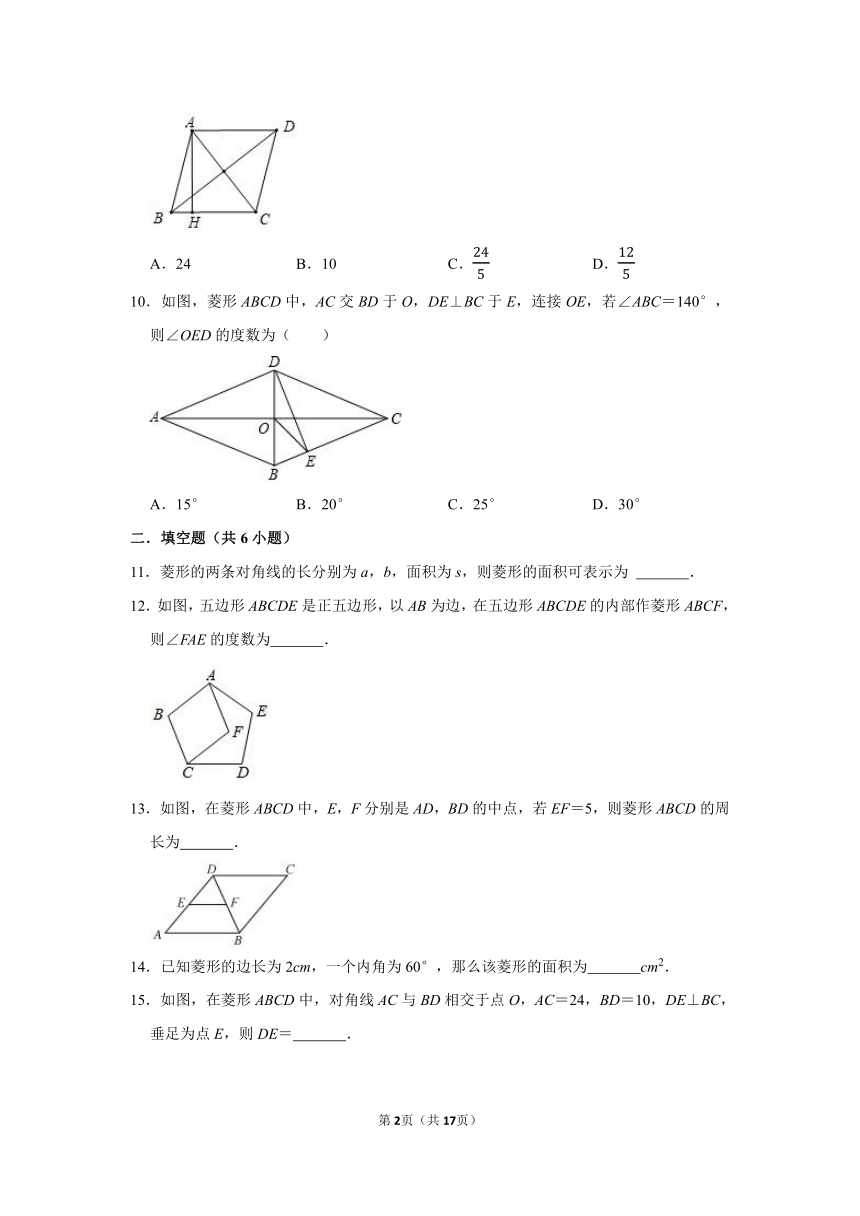
10.如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED的度数为( )
A.15° B.20° C.25° D.30°
二.填空题(共6小题)
11.菱形的两条对角线的长分别为a,b,面积为s,则菱形的面积可表示为 .
12.如图,五边形ABCDE是正五边形,以AB为边,在五边形ABCDE的内部作菱形ABCF,则∠FAE的度数为 .
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为 .
14.已知菱形的边长为2cm,一个内角为60°,那么该菱形的面积为 cm2.
15.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=24,BD=10,DE⊥BC,垂足为点E,则DE= .
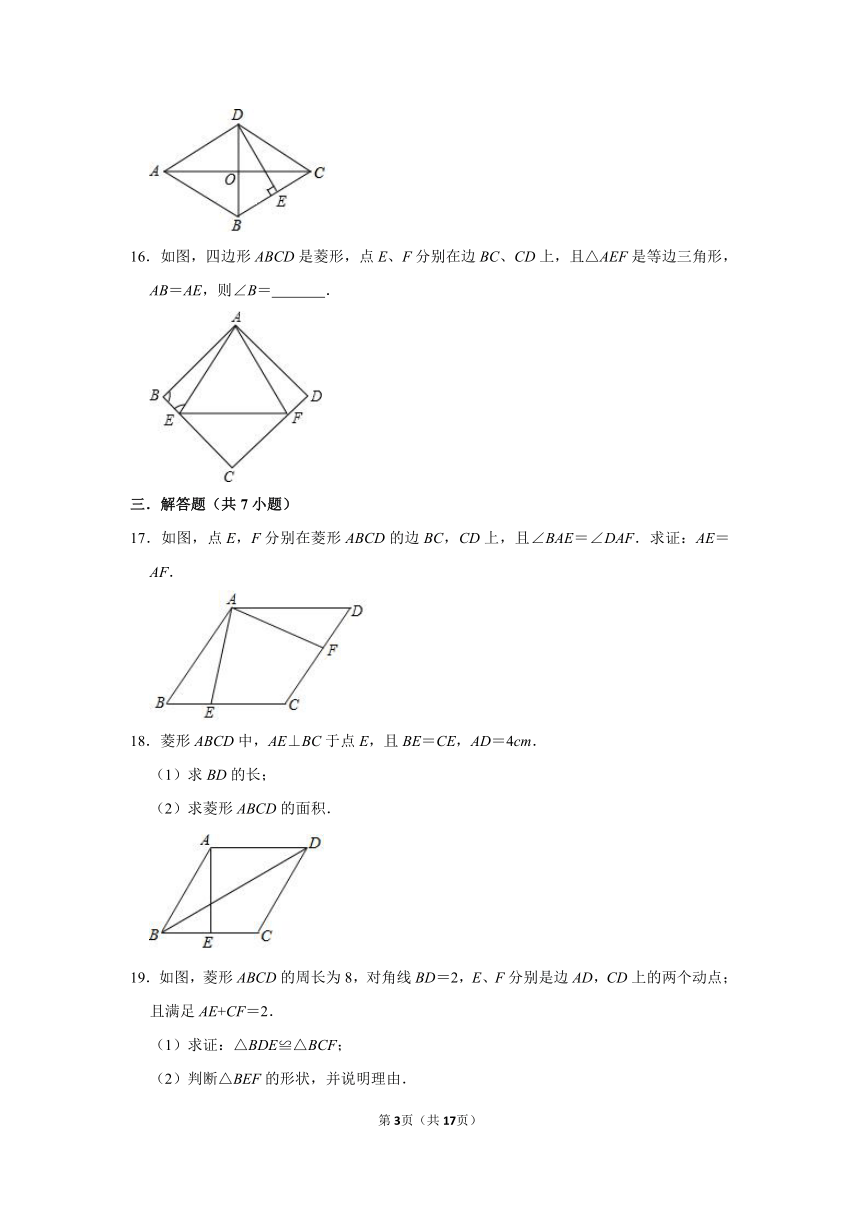
16.如图,四边形ABCD是菱形,点E、F分别在边BC、CD上,且△AEF是等边三角形,AB=AE,则∠B= .
三.解答题(共7小题)
17.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
18.菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=4cm.
(1)求BD的长;
(2)求菱形ABCD的面积.
19.如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
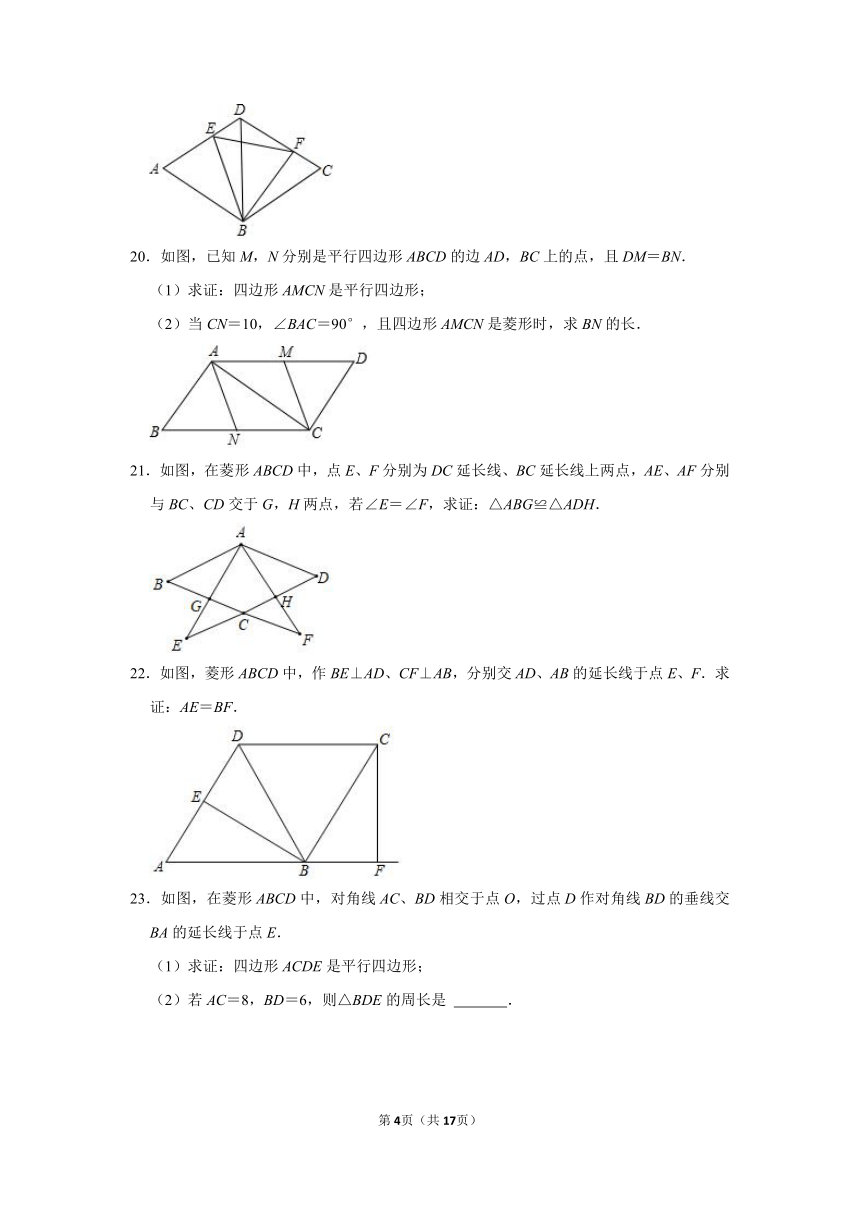
20.如图,已知M,N分别是平行四边形ABCD的边AD,BC上的点,且DM=BN.
(1)求证:四边形AMCN是平行四边形;
(2)当CN=10,∠BAC=90°,且四边形AMCN是菱形时,求BN的长.
21.如图,在菱形ABCD中,点E、F分别为DC延长线、BC延长线上两点,AE、AF分别与BC、CD交于G,H两点,若∠E=∠F,求证:△ABG≌△ADH.
22.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.求证:AE=BF.
23.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)求证:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,则△BDE的周长是 .
参考答案与试题解析
一.选择题(共10小题)
1.若菱形的两条对角线长分别为10和24,则菱形的面积为( )
A.13 B.26 C.120 D.240
【解析】∵菱形的两条对角线长分别为10和24,
∴菱形的面积为10×24=120,
故选:C.
2.若菱形的边长为2,则周长是( )
A.2 B.4 C.8 D.16
【解析】∵菱形的边长为2,
∴周长=2×4=8,
故选:C.
3.菱形的一个性质是( )
A.四个角相等 B.四条边相等 C.对角线相等 D.对角互补
【解析】菱形的一个性质是四条边相等,
故选项A、C、D错误,B 正确,
故选:B.
4.已知菱形ABCD中,∠D=150°,连接AC,则∠BAC等于( )
A.10° B.15° C.20° D.25°
【解析】∵菱形ABCD中,∠D=150°,
∴∠DAB=30°,∠BAC=∠DAC,
∴∠BAC=15°,
故选:B.
5.下列说法中不正确的是( )
A.平行四边形的对角相等
B.菱形的邻边相等
C.菱形的对角线互相垂直且相等
D.平行四边形的对角线互相平分
【解析】∵平行四边形的性质有对角相等,对角线互相平分,菱形的性质有四边相等,对角线互相垂直平分,
∴选项C符合题意,
故选:C.
6.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
【解析】A.菱形的四条边相等,正确,不符合题意,
B.菱形的对角线互相垂直且平分,对角线不一定相等,不正确,符合题意,
C.菱形的对角线互相垂直且平分,正确,不符合题意,
D.菱形是轴对称图形,正确,不符合题意,
故选:B.
7.如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
【解析】由四边形ABCD是菱形可得:AB=AD,∠B=∠D,
A、添加BE=DF,可用SAS证明△ABE≌△ADF,故不符合题意;
B、添加∠BAE=∠DAF,可用ASA证明△ABE≌△ADF,故不符合题意;
C、添加AE=AD,不能证明△ABE≌△ADF,故符合题意;
D、添加∠AEB=∠AFD,可用AAS证明△ABE≌△ADF,故不符合题意;
故选:C.
8.菱形的面积为12cm2,一条对角线是6cm,那么菱形的另一条对角线长为( )
A.3cm B.4cm C.5cm D.6cm
【解析】设另一条对角线长为xcm,
则6 x=12,
解得x=4.
故选:B.
9.如图,菱形ABCD中,AC=6,BD=8,AH⊥BC于点H,则AH=( )
A.24 B.10 C. D.
【解析】如图,对角线AC、BD交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,
∴BC5,
∵菱形ABCD的面积6×8=24,
∴AH,
故选:C.
10.如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED的度数为( )
A.15° B.20° C.25° D.30°
【解析】∵四边形ABCD是菱形,∠ABC=140°,
∴∠ABD=∠CBD∠ABC=70°,BO=DO,
∵DE⊥BC,
∴OE=OD=OB,∠BDE=20°,
∴∠ODE=∠OED=20°,
故选:B.
二.填空题(共6小题)
11.菱形的两条对角线的长分别为a,b,面积为s,则菱形的面积可表示为 ab .
【解析】如图.
∵四边形ABCD是菱形,AC=a,BD=b,
∴AC⊥BD,OA=OCACa,
∴菱形的面积S=S△ABD+S△CBDBD OABD OCb ab aab.
故答案为ab.
12.如图,五边形ABCDE是正五边形,以AB为边,在五边形ABCDE的内部作菱形ABCF,则∠FAE的度数为 36° .
【解析】∵五边形ABCDE是正五边形,
∴∠BAE=∠ABC=108°,
∵四边形ABCF是菱形,
∴∠ABC+∠BAF=180°,
∴∠BAF=180°﹣108°=72°,
∴∠FAE=∠BAE﹣∠BAF=108°﹣72°=36°.
故答案为:36°.
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为 40 .
【解析】∵E,F分别是AD,BD的中点,
∴EF是△ABD的中位线,
∴EFAB=5,
∴AB=10,
∵四边形ABD是菱形,
∴AB=BC=CD=AD=10,
∴菱形ABCD的周长=4AB=40;
故答案为:40.
14.已知菱形的边长为2cm,一个内角为60°,那么该菱形的面积为 2 cm2.
【解析】连接AC,过点A作AM⊥BC于点M,
∵菱形的边长为2cm,
∴AB=BC=2cm,
∵有一个内角是60°,
∴∠ABC=60°,
∴AM=ABsin60°,
∴此菱形的面积为:22(cm2).
故答案为:2.
15.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=24,BD=10,DE⊥BC,垂足为点E,则DE= .
【解析】∵四边形ABCD是菱形,
∴AD=BC,AC⊥BD,AO=OC,DO=BO,
∵AC=24,BD=10,
∴AO=12,OD=5,由勾股定理得:AD=13,
∴BC=13,
∴S菱形ABCDAC BD=BC×DE,
∴24×10=13×DE,
解得:DE,
故答案为:.
16.如图,四边形ABCD是菱形,点E、F分别在边BC、CD上,且△AEF是等边三角形,AB=AE,则∠B= 80° .
【解析】∵△AEF的边长与菱形ABCD的边长相等,
∴AB=AE,AF=AD,
设∠B=x,则∠BAD=180°﹣x,
∠BAE=∠DAF=180°﹣2x,
又∵∠BAE+∠EAF+∠FAD=∠BAD
即180°﹣2x+180°﹣2x+60°=180°﹣x
解得x=80°,
故答案为:80°
三.解答题(共7小题)
17.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
18.菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=4cm.
(1)求BD的长;
(2)求菱形ABCD的面积.
【解】(1)连接AC,交BD于点O,
∵AE⊥BC于点E,且BE=CE,
∴AB=AC,
∵在菱形ABCD中,
∴AB=BC,
∴△ABC是等边三角形,
∴∠ABO=30°,
∵AD=4,
∴AB=4,BO=2,
∴BD=4;
(2)菱形ABCD的面积为:AC BD4×48.
19.如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2﹣AE,
又∵DE=AD﹣AE=2﹣AE,
∴DE=CF,
在△BDE和△BCF中,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形.
20.如图,已知M,N分别是平行四边形ABCD的边AD,BC上的点,且DM=BN.
(1)求证:四边形AMCN是平行四边形;
(2)当CN=10,∠BAC=90°,且四边形AMCN是菱形时,求BN的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
又DM=BN,
∴AD﹣DM=CB﹣BN,
即AM=CN,
∵AM∥CN,
∴四边形AMCN是平行四边形;
(2)解:∵四边形AMCN是菱形,
∴AN=CN,
∴∠NAC=∠NCA,
又∠BAC=90°,即∠BAN+∠NAC=∠NCA+∠B=90°,
∴∠BAN=∠B,
∴AN=BN,
∴AN=BN=CN,
∴BN=10.
21.如图,在菱形ABCD中,点E、F分别为DC延长线、BC延长线上两点,AE、AF分别与BC、CD交于G,H两点,若∠E=∠F,求证:△ABG≌△ADH.
证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,AB∥CD,AD∥BC,
∴∠E=∠BAG,∠F=∠DAH,
∵∠E=∠F,
∴∠BAG=∠DAH,
在△ABG和△ADH中,
,
∴△ABG≌△ADH(ASA).
22.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.求证:AE=BF.
证明:四边形ABCD是菱形,
∴AB=BC,AD∥BC,
∴∠A=∠CBF,
∵BE⊥AD、CF⊥AB,
∴∠AEB=∠BFC=90°,
在△AEB和△BFC中,
,
∴△AEB≌△BFC(AAS),
∴AE=BF.
23.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)求证:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,则△BDE的周长是 24 .
(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∴AE∥CD,∠AOB=90°.
∵DE⊥BD,即∠EDB=90°,
∴∠AOB=∠EDB,
∴DE∥AC,
∴四边形ACDE是平行四边形;
(2)解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AD=CD5.
∵四边形ACDE是平行四边形,
∴AE=CD=5,DE=AC=8,
∴△BDE的周长=BD+BE+DE=6+10+8=24.
故答案为:24.第15页(共16页)
一.选择题(共10小题)
1.若菱形的两条对角线长分别为10和24,则菱形的面积为( )
A.13 B.26 C.120 D.240
2.若菱形的边长为2,则周长是( )
A.2 B.4 C.8 D.16
3.菱形的一个性质是( )
A.四个角相等 B.四条边相等 C.对角线相等 D.对角互补
4.已知菱形ABCD中,∠D=150°,连接AC,则∠BAC等于( )
A.10° B.15° C.20° D.25°
5.下列说法中不正确的是( )
A.平行四边形的对角相等
B.菱形的邻边相等
C.菱形的对角线互相垂直且相等
D.平行四边形的对角线互相平分
6.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
7.如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
8.菱形的面积为12cm2,一条对角线是6cm,那么菱形的另一条对角线长为( )
A.3cm B.4cm C.5cm D.6cm
9.如图,菱形ABCD中,AC=6,BD=8,AH⊥BC于点H,则AH=( )
A.24 B.10 C. D.
10.如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED的度数为( )
A.15° B.20° C.25° D.30°
二.填空题(共6小题)
11.菱形的两条对角线的长分别为a,b,面积为s,则菱形的面积可表示为 .
12.如图,五边形ABCDE是正五边形,以AB为边,在五边形ABCDE的内部作菱形ABCF,则∠FAE的度数为 .
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为 .
14.已知菱形的边长为2cm,一个内角为60°,那么该菱形的面积为 cm2.
15.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=24,BD=10,DE⊥BC,垂足为点E,则DE= .
16.如图,四边形ABCD是菱形,点E、F分别在边BC、CD上,且△AEF是等边三角形,AB=AE,则∠B= .
三.解答题(共7小题)
17.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
18.菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=4cm.
(1)求BD的长;
(2)求菱形ABCD的面积.
19.如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
20.如图,已知M,N分别是平行四边形ABCD的边AD,BC上的点,且DM=BN.
(1)求证:四边形AMCN是平行四边形;
(2)当CN=10,∠BAC=90°,且四边形AMCN是菱形时,求BN的长.
21.如图,在菱形ABCD中,点E、F分别为DC延长线、BC延长线上两点,AE、AF分别与BC、CD交于G,H两点,若∠E=∠F,求证:△ABG≌△ADH.
22.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.求证:AE=BF.
23.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)求证:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,则△BDE的周长是 .
参考答案与试题解析
一.选择题(共10小题)
1.若菱形的两条对角线长分别为10和24,则菱形的面积为( )
A.13 B.26 C.120 D.240
【解析】∵菱形的两条对角线长分别为10和24,
∴菱形的面积为10×24=120,
故选:C.
2.若菱形的边长为2,则周长是( )
A.2 B.4 C.8 D.16
【解析】∵菱形的边长为2,
∴周长=2×4=8,
故选:C.
3.菱形的一个性质是( )
A.四个角相等 B.四条边相等 C.对角线相等 D.对角互补
【解析】菱形的一个性质是四条边相等,
故选项A、C、D错误,B 正确,
故选:B.
4.已知菱形ABCD中,∠D=150°,连接AC,则∠BAC等于( )
A.10° B.15° C.20° D.25°
【解析】∵菱形ABCD中,∠D=150°,
∴∠DAB=30°,∠BAC=∠DAC,
∴∠BAC=15°,
故选:B.
5.下列说法中不正确的是( )
A.平行四边形的对角相等
B.菱形的邻边相等
C.菱形的对角线互相垂直且相等
D.平行四边形的对角线互相平分
【解析】∵平行四边形的性质有对角相等,对角线互相平分,菱形的性质有四边相等,对角线互相垂直平分,
∴选项C符合题意,
故选:C.
6.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
【解析】A.菱形的四条边相等,正确,不符合题意,
B.菱形的对角线互相垂直且平分,对角线不一定相等,不正确,符合题意,
C.菱形的对角线互相垂直且平分,正确,不符合题意,
D.菱形是轴对称图形,正确,不符合题意,
故选:B.
7.如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
【解析】由四边形ABCD是菱形可得:AB=AD,∠B=∠D,
A、添加BE=DF,可用SAS证明△ABE≌△ADF,故不符合题意;
B、添加∠BAE=∠DAF,可用ASA证明△ABE≌△ADF,故不符合题意;
C、添加AE=AD,不能证明△ABE≌△ADF,故符合题意;
D、添加∠AEB=∠AFD,可用AAS证明△ABE≌△ADF,故不符合题意;
故选:C.
8.菱形的面积为12cm2,一条对角线是6cm,那么菱形的另一条对角线长为( )
A.3cm B.4cm C.5cm D.6cm
【解析】设另一条对角线长为xcm,
则6 x=12,
解得x=4.
故选:B.
9.如图,菱形ABCD中,AC=6,BD=8,AH⊥BC于点H,则AH=( )
A.24 B.10 C. D.
【解析】如图,对角线AC、BD交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,
∴BC5,
∵菱形ABCD的面积6×8=24,
∴AH,
故选:C.
10.如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED的度数为( )
A.15° B.20° C.25° D.30°
【解析】∵四边形ABCD是菱形,∠ABC=140°,
∴∠ABD=∠CBD∠ABC=70°,BO=DO,
∵DE⊥BC,
∴OE=OD=OB,∠BDE=20°,
∴∠ODE=∠OED=20°,
故选:B.
二.填空题(共6小题)
11.菱形的两条对角线的长分别为a,b,面积为s,则菱形的面积可表示为 ab .
【解析】如图.
∵四边形ABCD是菱形,AC=a,BD=b,
∴AC⊥BD,OA=OCACa,
∴菱形的面积S=S△ABD+S△CBDBD OABD OCb ab aab.
故答案为ab.
12.如图,五边形ABCDE是正五边形,以AB为边,在五边形ABCDE的内部作菱形ABCF,则∠FAE的度数为 36° .
【解析】∵五边形ABCDE是正五边形,
∴∠BAE=∠ABC=108°,
∵四边形ABCF是菱形,
∴∠ABC+∠BAF=180°,
∴∠BAF=180°﹣108°=72°,
∴∠FAE=∠BAE﹣∠BAF=108°﹣72°=36°.
故答案为:36°.
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为 40 .
【解析】∵E,F分别是AD,BD的中点,
∴EF是△ABD的中位线,
∴EFAB=5,
∴AB=10,
∵四边形ABD是菱形,
∴AB=BC=CD=AD=10,
∴菱形ABCD的周长=4AB=40;
故答案为:40.
14.已知菱形的边长为2cm,一个内角为60°,那么该菱形的面积为 2 cm2.
【解析】连接AC,过点A作AM⊥BC于点M,
∵菱形的边长为2cm,
∴AB=BC=2cm,
∵有一个内角是60°,
∴∠ABC=60°,
∴AM=ABsin60°,
∴此菱形的面积为:22(cm2).
故答案为:2.
15.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=24,BD=10,DE⊥BC,垂足为点E,则DE= .
【解析】∵四边形ABCD是菱形,
∴AD=BC,AC⊥BD,AO=OC,DO=BO,
∵AC=24,BD=10,
∴AO=12,OD=5,由勾股定理得:AD=13,
∴BC=13,
∴S菱形ABCDAC BD=BC×DE,
∴24×10=13×DE,
解得:DE,
故答案为:.
16.如图,四边形ABCD是菱形,点E、F分别在边BC、CD上,且△AEF是等边三角形,AB=AE,则∠B= 80° .
【解析】∵△AEF的边长与菱形ABCD的边长相等,
∴AB=AE,AF=AD,
设∠B=x,则∠BAD=180°﹣x,
∠BAE=∠DAF=180°﹣2x,
又∵∠BAE+∠EAF+∠FAD=∠BAD
即180°﹣2x+180°﹣2x+60°=180°﹣x
解得x=80°,
故答案为:80°
三.解答题(共7小题)
17.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
18.菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=4cm.
(1)求BD的长;
(2)求菱形ABCD的面积.
【解】(1)连接AC,交BD于点O,
∵AE⊥BC于点E,且BE=CE,
∴AB=AC,
∵在菱形ABCD中,
∴AB=BC,
∴△ABC是等边三角形,
∴∠ABO=30°,
∵AD=4,
∴AB=4,BO=2,
∴BD=4;
(2)菱形ABCD的面积为:AC BD4×48.
19.如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2﹣AE,
又∵DE=AD﹣AE=2﹣AE,
∴DE=CF,
在△BDE和△BCF中,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形.
20.如图,已知M,N分别是平行四边形ABCD的边AD,BC上的点,且DM=BN.
(1)求证:四边形AMCN是平行四边形;
(2)当CN=10,∠BAC=90°,且四边形AMCN是菱形时,求BN的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
又DM=BN,
∴AD﹣DM=CB﹣BN,
即AM=CN,
∵AM∥CN,
∴四边形AMCN是平行四边形;
(2)解:∵四边形AMCN是菱形,
∴AN=CN,
∴∠NAC=∠NCA,
又∠BAC=90°,即∠BAN+∠NAC=∠NCA+∠B=90°,
∴∠BAN=∠B,
∴AN=BN,
∴AN=BN=CN,
∴BN=10.
21.如图,在菱形ABCD中,点E、F分别为DC延长线、BC延长线上两点,AE、AF分别与BC、CD交于G,H两点,若∠E=∠F,求证:△ABG≌△ADH.
证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,AB∥CD,AD∥BC,
∴∠E=∠BAG,∠F=∠DAH,
∵∠E=∠F,
∴∠BAG=∠DAH,
在△ABG和△ADH中,
,
∴△ABG≌△ADH(ASA).
22.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.求证:AE=BF.
证明:四边形ABCD是菱形,
∴AB=BC,AD∥BC,
∴∠A=∠CBF,
∵BE⊥AD、CF⊥AB,
∴∠AEB=∠BFC=90°,
在△AEB和△BFC中,
,
∴△AEB≌△BFC(AAS),
∴AE=BF.
23.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)求证:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,则△BDE的周长是 24 .
(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∴AE∥CD,∠AOB=90°.
∵DE⊥BD,即∠EDB=90°,
∴∠AOB=∠EDB,
∴DE∥AC,
∴四边形ACDE是平行四边形;
(2)解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AD=CD5.
∵四边形ACDE是平行四边形,
∴AE=CD=5,DE=AC=8,
∴△BDE的周长=BD+BE+DE=6+10+8=24.
故答案为:24.第15页(共16页)
