2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册 第五章一次函数的导数及其应用单元测试word版含答案
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册 第五章一次函数的导数及其应用单元测试word版含答案 | 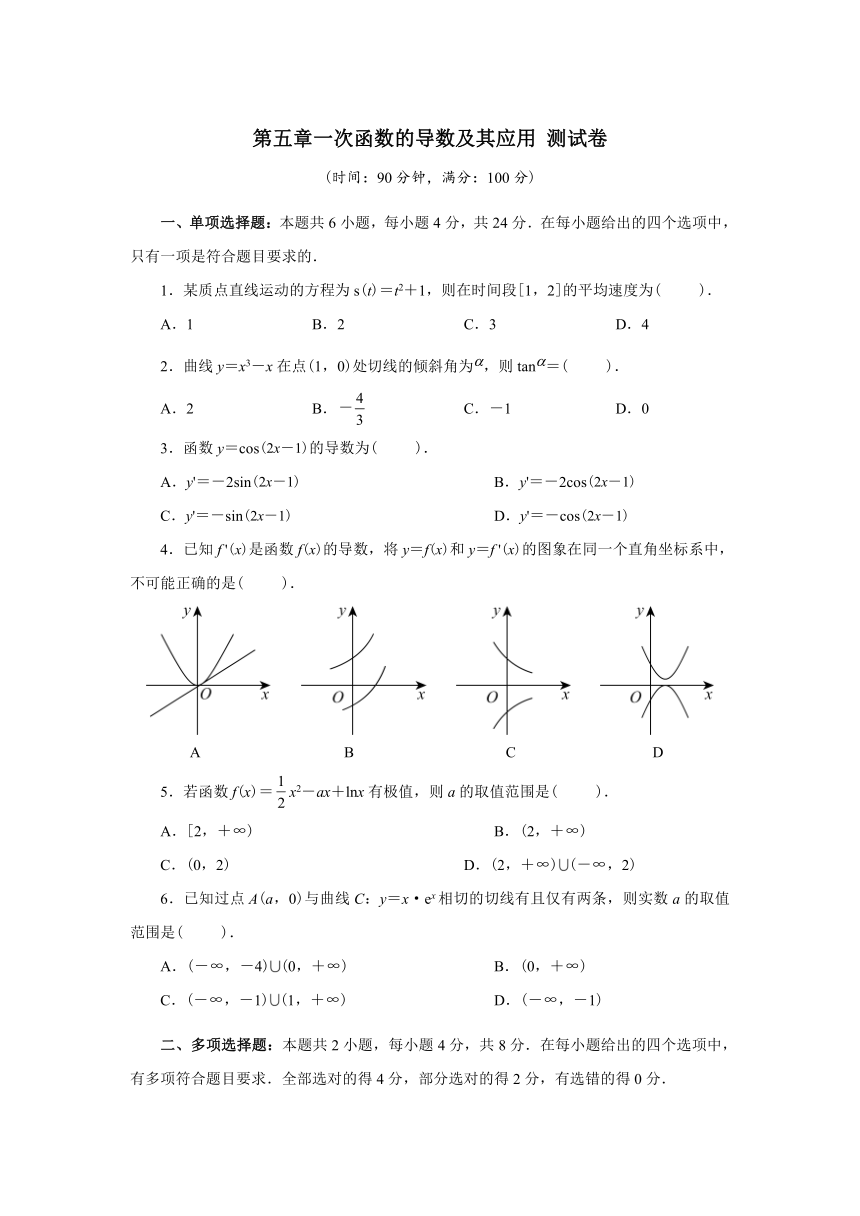 | |
| 格式 | docx | ||
| 文件大小 | 264.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 20:07:47 | ||
图片预览




文档简介
第五章一次函数的导数及其应用 测试卷
(时间:90分钟,满分:100分)
一、单项选择题:本题共6小题,每小题4分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某质点直线运动的方程为s(t)=t2+1,则在时间段[1,2]的平均速度为( ).
A.1 B.2 C.3 D.4
2.曲线y=x3-x在点(1,0)处切线的倾斜角为,则tan=( ).
A.2 B. C.-1 D.0
3.函数y=cos(2x-1)的导数为( ).
A.y'=-2sin(2x-1) B.y'=-2cos(2x-1)
C.y'=-sin(2x-1) D.y'=-cos(2x-1)
4.已知f '(x)是函数f(x)的导数,将y=f(x)和y=f '(x)的图象在同一个直角坐标系中,不可能正确的是( ).
A B C D
5.若函数f(x)=x2-ax+lnx有极值,则a的取值范围是( ).
A.[2,+∞) B.(2,+∞)
C.(0,2) D.(2,+∞)(-∞,2)
6.已知过点A(a,0)与曲线C:y=x·ex相切的切线有且仅有两条,则实数a的取值范围是( ).
A.(-∞,-4)(0,+∞) B.(0,+∞)
C.(-∞,-1)(1,+∞) D.(-∞,-1)
二、多项选择题:本题共2小题,每小题4分,共8分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得4分,部分选对的得2分,有选错的得0分.
7.已知函数f(x)=xln(1+x),则( ).
A.f(x)在(0,+∞)上单调递增
B.f(x)有两个零点
C.曲线y=f(x)在点处切线的斜率为-1-ln 2
D.f(x)是偶函数
8.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=e-x(x-1).则下列结论正确的是( ).
A.当x<0时,f(x)=ex(x+1)
B.函数f(x)有五个零点
C.若关于x的方程f(x)=m有解,则实数m的取值范围是f(-2)≤m≤f(2)
D.x1,x2R,|f(x2)-f(x1)|<2恒成立
三、填空题:本题共5小题,每小题4分,共20分.将答案填在题后的横线上.
9.若f '(x0)=2,则=____________.
10.已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f '(x)>0的解集为____________.
11.已知l1,l2是曲线C:y=的两条互相平行的切线,则l1与l2的距离的最大值为____________.
12.已知函数f(x)=sin2x+2cosx,则函数f(x)在[0,]上的最大值为____________.
13.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x3-3x2+a,则f(-2)=____________,曲线y=f(x)在点(-2,f(-2))处的切线方程为____________.
四、解答题:本题共5小题,共48分.解答应写出文字说明、证明过程或演算步骤.
14.(8分)已知函数f(x)=x3-ax+b,在点M(1,f(1))处的切线方程为9x+3y-10=0,求实数a,b的值.
15.(10分)已知aR,函数f(x)=x3+ax2+2ax(aR).
(1)当a=1时,求函数f(x)的单调递增区间;
(2)若不等式f '(x)≤0在R上恒成立,求a的取值范围.
16.(10分)已知曲线y=与y=(x-1)2恰好存在两条公切线,求实数a的取值范围.
17.(10分)已知函数f(x)=(a+1)lnx+ax2+1.
(1)讨论函数f(x)的单调性.
(2)设a≤2,求证:对任意x1,x2(0,+∞),都有|f(x1)-f(x2)|≥4|x1-x2|.
18.(10分)一个仓库由上下两部分组成:上部分形状是正四棱锥P- A1B1C1D1,下部分形状是正四棱柱ABCD-A1B1C1D1(如图所示),并且正四棱柱的高O1O是正四棱锥的高PO1的4倍.
(1)若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为6 m,当PO1为多少时,仓库的容积最大?
参考答案
一、单项选择题.
1.C.
2.A.
3.A.
4.D.
5.B.
6.A.
二、多项选择题.
7.AC.提示:容易得到,A,C都正确;因为函数f(x)的定义域为(-1,+∞),所以f(x)不是偶函数,故D错误;由f(x)=x ln(l+x)=0,解得x=0,所以f(x)恰有一个零点,故B错误.故选AC.
8.AD.提示:设x<0,则-x>0,所以f(-x)=ex(-x-1),
又函数f(x)是定义在R上的奇函数,所以f(-x)=-f(x),
所以-f(x)=ex(-x-1),即f(x)=ex(x+1),故A正确.
当x>0时,f(x)=,所以,
令f '(x)=0,解得x=2.当0<x<2时,f '(x)>0;当x>2时,f '(x)<0,
所以函数f(x)在(0,2)内单调递增,在(2,+∞)内单调递减,
故当x=2时,函数f(x)取得极大值e-2>0.
当0<x<2时,f(0)·f(2)<0,又f(1)=0,故函数f(x)在(0,2)内仅有一个零点1.
当x>2时,f(x)=>0,所以函数f(x)在(2,+∞)上没有零点,
所以函数f(x)在(0,+∞)上仅有一个零点.
又因为函数f(x)是定义在R上的奇函数,
所以函数f(x)在(-∞,0)上仅有一个零点-1.
又f(0)=0,故函数f(x)是定义在R上有3个零点.故B错误.
作出函数f(x)的大致图象,由图可知,
若关于x的方程f(x)=m有解,则实数m的取值范围是-1<m<1.故C错误.
由图可知,对x1,x2R,|f(x2)-f(x1)|<|1-(-1)|=2,故D正确.故选AD.
三、填空题.
9.1.
10.(-∞,-1)(-1,1)(3,+∞).
11..
12..
13.-4,12x-y+20=0.
提示:f(x)是定义在R上的奇函数,则f(0)=a=0,故a=0,f(-2)=-f(2)=-(16-12)=-4,
当x<0时,-x>0,故f(-x)=-2x3-3x2,f(x)=-f(-x)=2x3+3x2,
f '(x)=6x2+6x,f '(-2)=12,故切线方程为y=12(x+2)-4,
即12x-y+20=0.故答案为-4,12x-y+20=0.
四、解答题.
14.解:因为在点M(1,f(1))处的切线方程为9x+3y-10=0,所以切线斜率是=-3,
且9×1+3f(1)-10=0,求得f(1)=,即点M(1,).
又函数f(x)=x3-ax+b,则f '(x)=x2-a,
所以依题意得 解得
15.解:(1)当a=1时,f(x)=x3+x2+2x,所以f '(x)=-x2+x+2.
令f '(x)>0,则-x2+x+2>0,即x2-x-2<0,解得-1<x<2,所以函数f(x)的单调递增区间是(-1,2).
(2)已知f '(x)≤0对xR都成立,即-x2+ax+2a≤0对xR都成立.
即x2-ax-2a≥0对xR都成立,所以=a2+8a≤0,解得-8≤a≤0.
16.解:y=(x-1)2的导数为y'=2(x-1),y=的导数为y'=.设与曲线y=相切的切点为(m,n),与曲线y=(x-1)2相切的切点为(s,t),则有公切线的斜率为
2(s-1)=.又t=(s-1)2,n=,有
2(s-1)=,即为,即有(s>1).
又=2(s-1),所以(s>1).
令f(s)=(s>1),则f '(s)=.
当s>3时,f '(s)<0,f(s)单调递减;当1<s<3时,f '(s)>0,f(s)单调递增,
即当s=3时,f(s)取得极大值,也为最大值,且为2ln2-3.
由恰好存在两条公切线,即s有两解,可得a的取值范围是a<2ln2-3.
17.解:(1)由题意,知f(x)的定义域为(0,+∞),f '(x)=.
当a≥0时,f '(x)>0,故f(x)在(0,+∞)上单调递增;
当a≤-1时,f '(x)<0,故f(x)在(0,+∞)上单调递减;
当-1<a<0时,令f '(x)=0,解得x=.
当x(0,)时,f '(x)>0;当x(,+∞)时,f '(x)<0.
故f(x)在(0,)上单调递增,在(,+∞)上单调递减.
(2)不妨假设x1≥x2,由(1)可知,当a≤-2时,f(x)在(0,+∞)上单调递减,所以
|f(x1)-f(x2)|≥4|x1-x2|f(x2)-f(x1)≥4x1-4x2,即f(x2)+4x2≥f(x1)+4x1.
令g(x)=f(x)+4x,则g'(x)=.
于是g'(x)≤.
从而g(x)在(0,+∞)上单调递减,故g(x1)≤g(x2),即f(x1)+4x1≤f(x2)+4x2.
故对任意x1,x2(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|.
18.解:(1)由PO1=2,得OO1=4PO1=8.因为A1B1=AB=6,
所以正四棱锥P-A1B1C1D1的体积V锥=·A1B12·PO1=×62×2=24(m3).
正四棱柱ABCD-A1B1C1D1的体积V柱=AB2·OO1=62×8=288(m3).
所以仓库的容积V=V锥+V柱=24+288=312(m3).
(2)设A1B1=a(m),PO1=h(m),则0<<6,OO1=4h.连结O1B1.
因为在Rt△PO1B1中,O1B12+PO12=PB12,所以()2+h2=36,
即a2=2(36-h2).于是仓库的容积
V=V柱+V锥=a2·4h+a2·h=a2h=(36h-h3)(0<h<6),
从而V'=(36-3h2)=26(12-h2).
令V'=0,得h=或h=(舍).
(i)当0<h<时,V'>0,V是单调增函数;
(ii)当<h<6时,V'<0,V是单调减函数.
故h=时,V取得极大值,也是最大值.
因此,当PO1=m时,仓库的容积最大.
(时间:90分钟,满分:100分)
一、单项选择题:本题共6小题,每小题4分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某质点直线运动的方程为s(t)=t2+1,则在时间段[1,2]的平均速度为( ).
A.1 B.2 C.3 D.4
2.曲线y=x3-x在点(1,0)处切线的倾斜角为,则tan=( ).
A.2 B. C.-1 D.0
3.函数y=cos(2x-1)的导数为( ).
A.y'=-2sin(2x-1) B.y'=-2cos(2x-1)
C.y'=-sin(2x-1) D.y'=-cos(2x-1)
4.已知f '(x)是函数f(x)的导数,将y=f(x)和y=f '(x)的图象在同一个直角坐标系中,不可能正确的是( ).
A B C D
5.若函数f(x)=x2-ax+lnx有极值,则a的取值范围是( ).
A.[2,+∞) B.(2,+∞)
C.(0,2) D.(2,+∞)(-∞,2)
6.已知过点A(a,0)与曲线C:y=x·ex相切的切线有且仅有两条,则实数a的取值范围是( ).
A.(-∞,-4)(0,+∞) B.(0,+∞)
C.(-∞,-1)(1,+∞) D.(-∞,-1)
二、多项选择题:本题共2小题,每小题4分,共8分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得4分,部分选对的得2分,有选错的得0分.
7.已知函数f(x)=xln(1+x),则( ).
A.f(x)在(0,+∞)上单调递增
B.f(x)有两个零点
C.曲线y=f(x)在点处切线的斜率为-1-ln 2
D.f(x)是偶函数
8.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=e-x(x-1).则下列结论正确的是( ).
A.当x<0时,f(x)=ex(x+1)
B.函数f(x)有五个零点
C.若关于x的方程f(x)=m有解,则实数m的取值范围是f(-2)≤m≤f(2)
D.x1,x2R,|f(x2)-f(x1)|<2恒成立
三、填空题:本题共5小题,每小题4分,共20分.将答案填在题后的横线上.
9.若f '(x0)=2,则=____________.
10.已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f '(x)>0的解集为____________.
11.已知l1,l2是曲线C:y=的两条互相平行的切线,则l1与l2的距离的最大值为____________.
12.已知函数f(x)=sin2x+2cosx,则函数f(x)在[0,]上的最大值为____________.
13.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x3-3x2+a,则f(-2)=____________,曲线y=f(x)在点(-2,f(-2))处的切线方程为____________.
四、解答题:本题共5小题,共48分.解答应写出文字说明、证明过程或演算步骤.
14.(8分)已知函数f(x)=x3-ax+b,在点M(1,f(1))处的切线方程为9x+3y-10=0,求实数a,b的值.
15.(10分)已知aR,函数f(x)=x3+ax2+2ax(aR).
(1)当a=1时,求函数f(x)的单调递增区间;
(2)若不等式f '(x)≤0在R上恒成立,求a的取值范围.
16.(10分)已知曲线y=与y=(x-1)2恰好存在两条公切线,求实数a的取值范围.
17.(10分)已知函数f(x)=(a+1)lnx+ax2+1.
(1)讨论函数f(x)的单调性.
(2)设a≤2,求证:对任意x1,x2(0,+∞),都有|f(x1)-f(x2)|≥4|x1-x2|.
18.(10分)一个仓库由上下两部分组成:上部分形状是正四棱锥P- A1B1C1D1,下部分形状是正四棱柱ABCD-A1B1C1D1(如图所示),并且正四棱柱的高O1O是正四棱锥的高PO1的4倍.
(1)若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为6 m,当PO1为多少时,仓库的容积最大?
参考答案
一、单项选择题.
1.C.
2.A.
3.A.
4.D.
5.B.
6.A.
二、多项选择题.
7.AC.提示:容易得到,A,C都正确;因为函数f(x)的定义域为(-1,+∞),所以f(x)不是偶函数,故D错误;由f(x)=x ln(l+x)=0,解得x=0,所以f(x)恰有一个零点,故B错误.故选AC.
8.AD.提示:设x<0,则-x>0,所以f(-x)=ex(-x-1),
又函数f(x)是定义在R上的奇函数,所以f(-x)=-f(x),
所以-f(x)=ex(-x-1),即f(x)=ex(x+1),故A正确.
当x>0时,f(x)=,所以,
令f '(x)=0,解得x=2.当0<x<2时,f '(x)>0;当x>2时,f '(x)<0,
所以函数f(x)在(0,2)内单调递增,在(2,+∞)内单调递减,
故当x=2时,函数f(x)取得极大值e-2>0.
当0<x<2时,f(0)·f(2)<0,又f(1)=0,故函数f(x)在(0,2)内仅有一个零点1.
当x>2时,f(x)=>0,所以函数f(x)在(2,+∞)上没有零点,
所以函数f(x)在(0,+∞)上仅有一个零点.
又因为函数f(x)是定义在R上的奇函数,
所以函数f(x)在(-∞,0)上仅有一个零点-1.
又f(0)=0,故函数f(x)是定义在R上有3个零点.故B错误.
作出函数f(x)的大致图象,由图可知,
若关于x的方程f(x)=m有解,则实数m的取值范围是-1<m<1.故C错误.
由图可知,对x1,x2R,|f(x2)-f(x1)|<|1-(-1)|=2,故D正确.故选AD.
三、填空题.
9.1.
10.(-∞,-1)(-1,1)(3,+∞).
11..
12..
13.-4,12x-y+20=0.
提示:f(x)是定义在R上的奇函数,则f(0)=a=0,故a=0,f(-2)=-f(2)=-(16-12)=-4,
当x<0时,-x>0,故f(-x)=-2x3-3x2,f(x)=-f(-x)=2x3+3x2,
f '(x)=6x2+6x,f '(-2)=12,故切线方程为y=12(x+2)-4,
即12x-y+20=0.故答案为-4,12x-y+20=0.
四、解答题.
14.解:因为在点M(1,f(1))处的切线方程为9x+3y-10=0,所以切线斜率是=-3,
且9×1+3f(1)-10=0,求得f(1)=,即点M(1,).
又函数f(x)=x3-ax+b,则f '(x)=x2-a,
所以依题意得 解得
15.解:(1)当a=1时,f(x)=x3+x2+2x,所以f '(x)=-x2+x+2.
令f '(x)>0,则-x2+x+2>0,即x2-x-2<0,解得-1<x<2,所以函数f(x)的单调递增区间是(-1,2).
(2)已知f '(x)≤0对xR都成立,即-x2+ax+2a≤0对xR都成立.
即x2-ax-2a≥0对xR都成立,所以=a2+8a≤0,解得-8≤a≤0.
16.解:y=(x-1)2的导数为y'=2(x-1),y=的导数为y'=.设与曲线y=相切的切点为(m,n),与曲线y=(x-1)2相切的切点为(s,t),则有公切线的斜率为
2(s-1)=.又t=(s-1)2,n=,有
2(s-1)=,即为,即有(s>1).
又=2(s-1),所以(s>1).
令f(s)=(s>1),则f '(s)=.
当s>3时,f '(s)<0,f(s)单调递减;当1<s<3时,f '(s)>0,f(s)单调递增,
即当s=3时,f(s)取得极大值,也为最大值,且为2ln2-3.
由恰好存在两条公切线,即s有两解,可得a的取值范围是a<2ln2-3.
17.解:(1)由题意,知f(x)的定义域为(0,+∞),f '(x)=.
当a≥0时,f '(x)>0,故f(x)在(0,+∞)上单调递增;
当a≤-1时,f '(x)<0,故f(x)在(0,+∞)上单调递减;
当-1<a<0时,令f '(x)=0,解得x=.
当x(0,)时,f '(x)>0;当x(,+∞)时,f '(x)<0.
故f(x)在(0,)上单调递增,在(,+∞)上单调递减.
(2)不妨假设x1≥x2,由(1)可知,当a≤-2时,f(x)在(0,+∞)上单调递减,所以
|f(x1)-f(x2)|≥4|x1-x2|f(x2)-f(x1)≥4x1-4x2,即f(x2)+4x2≥f(x1)+4x1.
令g(x)=f(x)+4x,则g'(x)=.
于是g'(x)≤.
从而g(x)在(0,+∞)上单调递减,故g(x1)≤g(x2),即f(x1)+4x1≤f(x2)+4x2.
故对任意x1,x2(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|.
18.解:(1)由PO1=2,得OO1=4PO1=8.因为A1B1=AB=6,
所以正四棱锥P-A1B1C1D1的体积V锥=·A1B12·PO1=×62×2=24(m3).
正四棱柱ABCD-A1B1C1D1的体积V柱=AB2·OO1=62×8=288(m3).
所以仓库的容积V=V锥+V柱=24+288=312(m3).
(2)设A1B1=a(m),PO1=h(m),则0<<6,OO1=4h.连结O1B1.
因为在Rt△PO1B1中,O1B12+PO12=PB12,所以()2+h2=36,
即a2=2(36-h2).于是仓库的容积
V=V柱+V锥=a2·4h+a2·h=a2h=(36h-h3)(0<h<6),
从而V'=(36-3h2)=26(12-h2).
令V'=0,得h=或h=(舍).
(i)当0<h<时,V'>0,V是单调增函数;
(ii)当<h<6时,V'<0,V是单调减函数.
故h=时,V取得极大值,也是最大值.
因此,当PO1=m时,仓库的容积最大.
