2021-2022学年高一下学期数学人教B版(2019)必修第三册 7.3.4正切函数的性质与图像教案 word版
文档属性
| 名称 | 2021-2022学年高一下学期数学人教B版(2019)必修第三册 7.3.4正切函数的性质与图像教案 word版 |

|
|
| 格式 | docx | ||
| 文件大小 | 81.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览




文档简介
7.3.4正切函数的性质与图像
【教学目标】
1.了解正切函数图像的画法,理解掌握正切函数的性质.
2.能利用正切函数的图像及性质解决有关问题.
【教学重点】
正切函数的图像及其主要性质(包括周期性、单调性、奇偶性、最值或值域).
【教学难点】
对正切函数周期性的理解.
【教学过程】
一、课前预习
预习课本,思考并完成以下问题
(1)正切函数有哪些性质?
(2)正切函数在定义域内是不是单调函数?
二、课前小测
1.在下列函数中同时满足:①在上递增;②以2π为周期;③是奇函数的是( )
A.y=tan x B.y=cos x
C.y=tan D.y=-tan x
答案:C
解析:A,D的周期为π,B中函数在上递减,故选C.
2.函数y=tan的定义域为________.
答案:
解析:因为2x-≠kπ+,k∈Z,
所以x≠+,k∈Z
所以函数y=tan的定义域为
.
3.函数y=tan 3x的最小正周期是________.
答案:
解析:函数y=tan 3x的最小正周期是.
4.函数y=tan的单调增区间是________.
答案:,k∈Z
解析:令kπ-<x-<kπ+,k∈Z
得kπ-<x<kπ+,k∈Z
即函数y=tan的单调增区间是,k∈Z.
三、新知探究
正切函数的图像与性质
解析式 y=tan x
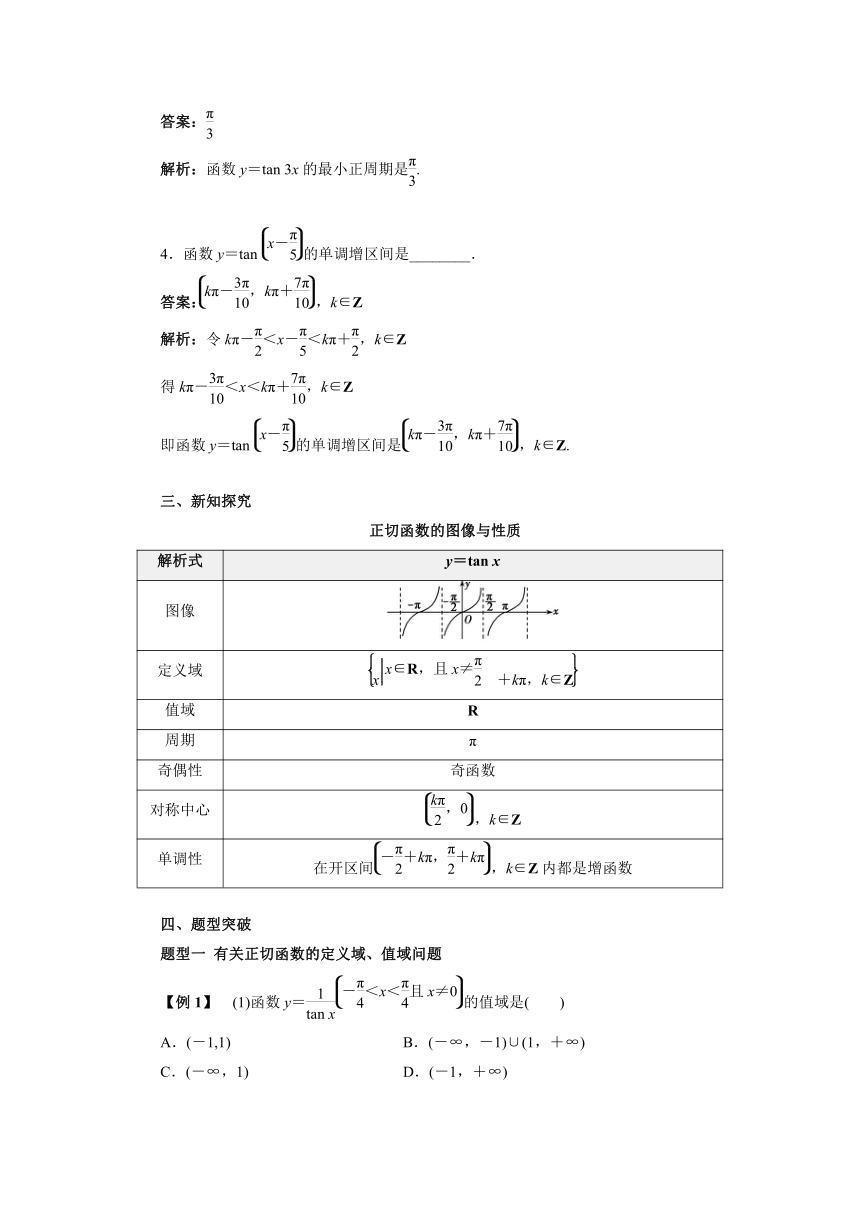
图像
定义域
值域 R
周期 π
奇偶性 奇函数
对称中心 ,k∈Z
单调性 在开区间,k∈Z内都是增函数
四、题型突破
题型一 有关正切函数的定义域、值域问题
【例1】 (1)函数y=的值域是( )
A.(-1,1) B.(-∞,-1)∪(1,+∞)
C.(-∞,1) D.(-1,+∞)
(2)函数y=3tan的定义域为________.
(3)函数y=+lg(1-tan x)的定义域为________.
[思路点拨] 求定义域时,要注意正切函数自身的限制条件,另外解不等式时要充分利用三角函数的图像或三角函数线.
答案:(1)B (2) (3)
解析:(1)当-<x<0时,-1<tan x<0,∴≤-1;
当0<x<时,0<tan x<1,∴≥1.
即当x∈∪时,函数y=的值域是(-∞,-1)∪(1,+∞).
(2)要使函数有意义应满足-≠kπ+,k∈Z,得x≠-4kπ-,k∈Z,
所以函数的定义域为.
(3)要使函数y=+lg(1-tan x)有意义,则
即-1≤tan x<1.
在上满足上述不等式的x的取值范围是.
又因为y=tan x的周期为π,所以所求x的定义域为.
【反思感悟】
1.求正切函数定义域的方法
(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义即x≠+kπ,k∈Z.
(2)求正切型函数y=Atan(ωx+φ)(A≠0,ω>0)的定义域时,要将“ωx+φ”视为一个“整体”.令ωx+φ≠kπ+,k∈Z,解得x.
2.解形如tan x>a的不等式的步骤
提醒:求定义域时,要注意正切函数自身的限制条件.
【跟踪训练】
1.函数y=tan的定义域是( )
A.
B.
C.
D.
答案:B
解析:由题意tan>0,
即tan<0,
∴kπ-<x-<kπ,
∴kπ-<x<kπ+,k∈Z,故选B.
2.求函数y=tan2+tan+1的定义域和值域.
解:由3x+≠kπ+,k∈Z,得x≠+(k∈Z),
所以函数的定义域为.
设t=tan,
则t∈R,y=t2+t+1=2+≥,
所以原函数的值域是.
题型二 正切函数奇偶性、周期性和图像的对称性
【例2】 (1)函数f(x)=tan的周期为________.
(2)已知函数y=tan,则该函数图像的对称中心坐标为________.
(3)判断下列函数的奇偶性:
①y=3xtan 2x-2x4;②y=cos+tan x.
[思路点拨] (1)形如y=Atan(ωx+φ)(Aω≠0)的周期T=,也可以用定义法求周期.
(2)形如y=Atan(ωx+φ)(Aω≠0)的对称中心横坐标可由ωx+φ=,k∈Z求出.
(3)先求定义域看是否关于原点对称,若对称再判断f(-x)与f(x)的关系.
答案:(1) (2),k∈Z
解析:(1)法一:(定义法)
∵tan=tan,
即tan=tan,
∴f(x)=tan的周期是.
法二:(公式法)
f(x)=tan的周期T=.
(2)由x-=(k∈Z)得x=+(k∈Z),所以图像的对称中心坐标为,k∈Z.]
(3)①定义域为,关于原点对称,
又f(-x)=3(-x)tan 2(-x)-2(-x)4=3xtan 2x-2x4=f(x),所以它是偶函数.
②定义域为,关于原点对称,
y=cos+tan x=sin x+tan x,
又f(-x)=sin(-x)+tan(-x)=-sin x-tan x=-f(x),所以它是奇函数.
【反思感悟】
1.函数f(x)=Atan(ωx+φ)周期的求解方法:
(1)定义法.
(2)公式法:对于函数f(x)=Atan(ωx+φ)的最小正周期T=.
(3)观察法(或图像法):观察函数的图像,看自变量间隔多少,函数值重复出现.
2.判定与正切函数有关的函数奇偶性的方法:
先求函数的定义域,看其定义域是否关于原点对称,若其不关于原点对称,则该函数为非奇非偶函数;若其关于原点对称,再看f(-x)与f(x)的关系.
提醒:y=tan x,x≠kπ+,k∈Z的对称中心坐标为,k∈Z.
【跟踪训练】
3.判断下列函数的奇偶性
(1)f(x)=;
(2)f(x)=tan+tan.
解:(1)由得
f(x)的定义域为,
不关于原点对称,
所以函数f(x)既不是偶函数,也不是奇函数.
(2) 函数定义域为,
关于原点对称,
又f(-x)=tan+tan
=-tan-tan
=-f(x),
所以函数f(x)是奇函数.
题型三 正切函数单调性的应用
[探究问题]
1.正切函数y=tan x在其定义域内是否为增函数?
提示:不是.正切函数的图像被直线x=kπ+(k∈Z)隔开,所以它的单调区间只在(k∈Z)内,而不能说它在定义域内是增函数.假设x1=,x2=π,x12.如果让你比较tan与tan的大小,你应该怎样做?
提示:先根据正切函数的周期性把两角化到同一单调区间内,再由正切函数的单调性进行比较.
【例3】 (1)tan 1,tan 2,tan 3,tan 4从小到大的排列顺序为________.
(2)求函数y=3tan的单调区间.
[思路点拨] (1)利用y=tan x在上为增函数比较大小,注意tan 1=tan(π+1).
(2)先将原函数化为y=-3tan,再由-+kπ<2x-<+kπ,k∈Z,求出单调减区间.
(1) 答案:tan 2<tan 3<tan 4<tan 1
解析:y=tan x在区间上是单调增函数,且tan 1=tan(π+1),
又<2<3<4<π+1<,
所以tan 2<tan 3<tan 4<tan 1.
(2)解:y=3tan=-3tan,
由-+kπ<2x-<+kπ,k∈Z得,
-+π<x<+π,k∈Z,
所以y=3tan的减区间为(-+π,+π),k∈Z.
【多维探究】
1.将本例(2)中的函数改为“y=3tan”,结果又如何?
解:由kπ-∴函数y=3tan的单调递增区间是(2kπ-,2kπ+π) (k∈Z).
2.将本例(2)中的函数改为“y=lgtan x”结果又如何?
解:因为函数y=lg x在(0,+∞)上为增函数.
所以函数y=lgtan x的单调递增区间
就是函数y=tan x(tan x>0)的递增区间,
即,k∈Z.
【反思感悟】
1.求函数y=Atan(ωx+φ)(A>0,ω≠0,且A,ω,φ都是常数)的单调区间的方法
(1)若ω>0,由于y=tan x在每一个单调区间上都是增函数,故可用“整体代换”的思想,令kπ-<ωx+φ<kπ+,k∈Z,解得x的范围即可.
(2)若ω<0,可利用诱导公式先把y=Atan(ωx+φ)转化为y=Atan[-(-ωx-φ)]=-Atan(-ωx-φ),即把x的系数化为正值,再利用“整体代换”的思想,求得x的范围即可.
2.运用正切函数单调性比较大小的步骤
(1)运用函数的周期性或诱导公式将角化到同一单调区间内.
(2)运用单调性比较大小关系.
提醒:y=Atan(ωx+φ)(A>0,ω>0)只有增区间;y=Atan(ωx+φ)(A<0,ω>0)只有减区间.
五、达标检测
1.思考辨析
(1)正切函数的定义域和值域都是R.( )
(2)正切函数图像是中心对称图形,有无数个对称中心.( )
(3)正切函数图像有无数条对称轴,其对称轴是x=kπ±,k∈Z.( )
(4)正切函数是增函数.( )
答案:(1)× (2)√ (3)× (4)×
2.若tan x≥1,则( )
A.2kπ-<x<2kπ(k∈Z)
B.x≤(2k+1)π(k∈Z)
C.kπ-<x≤kπ(k∈Z)
D.kπ+≤x<kπ+(k∈Z)
答案:D
解析:因为tan x≥1=tan.
所以+kπ≤x<+kπ,k∈Z.
3.求函数y=tan(π-x),x∈的值域为________.
答案:(-,1)
解析:y=tan(π-x)=-tan x,
在上为减函数,
所以值域为(-,1).
4.求函数y=tan的定义域、最小正周期、单调区间及其图像的对称中心.
解:①由-≠kπ+,k∈Z,得x≠2kπ+,k∈Z,
∴函数的定义域为.
②T==2π,
∴函数的最小正周期为2π.
③由kπ-<-<kπ+,k∈Z,得2kπ-<x<2kπ+,k∈Z,
∴函数的单调递增区间为, k∈Z.
④由-=,k∈Z,得x=kπ+,k∈Z,
∴函数图像的对称中心是,k∈Z.
六、本课小结
1.利用单位圆中的正切线作正切函数的图像,作图较为准确,但画图时较繁,我们常用“三点两线”法作正切曲线的简图.
2.正切函数与正弦函数、余弦函数的性质比较.
性质 正切函数 正弦函数、余弦函数
定义域 R
值域 R [-1,1]
最值 无 最大值为1
最小值为-1
单调性 仅有单调递增区间,不存在单调递减区间 单调递增区间、单调递减区间均存在
奇偶性 奇函数 正弦函数是奇函数
余弦函数是偶函数
周期性 T=π T=2π
对称性 有无数个对称中心,不存在对称轴 对称中心和对称轴均有无数个
七、课后作业
1.复习回顾本节内容.
2.完成本节配套课后练习《高一必修三 7.3.4正切函数的性质与图像课时精练(配套)》.
【教学目标】
1.了解正切函数图像的画法,理解掌握正切函数的性质.
2.能利用正切函数的图像及性质解决有关问题.
【教学重点】
正切函数的图像及其主要性质(包括周期性、单调性、奇偶性、最值或值域).
【教学难点】
对正切函数周期性的理解.
【教学过程】
一、课前预习
预习课本,思考并完成以下问题
(1)正切函数有哪些性质?
(2)正切函数在定义域内是不是单调函数?
二、课前小测
1.在下列函数中同时满足:①在上递增;②以2π为周期;③是奇函数的是( )
A.y=tan x B.y=cos x
C.y=tan D.y=-tan x
答案:C
解析:A,D的周期为π,B中函数在上递减,故选C.
2.函数y=tan的定义域为________.
答案:
解析:因为2x-≠kπ+,k∈Z,
所以x≠+,k∈Z
所以函数y=tan的定义域为
.
3.函数y=tan 3x的最小正周期是________.
答案:
解析:函数y=tan 3x的最小正周期是.
4.函数y=tan的单调增区间是________.
答案:,k∈Z
解析:令kπ-<x-<kπ+,k∈Z
得kπ-<x<kπ+,k∈Z
即函数y=tan的单调增区间是,k∈Z.
三、新知探究
正切函数的图像与性质
解析式 y=tan x
图像
定义域
值域 R
周期 π
奇偶性 奇函数
对称中心 ,k∈Z
单调性 在开区间,k∈Z内都是增函数
四、题型突破
题型一 有关正切函数的定义域、值域问题
【例1】 (1)函数y=的值域是( )
A.(-1,1) B.(-∞,-1)∪(1,+∞)
C.(-∞,1) D.(-1,+∞)
(2)函数y=3tan的定义域为________.
(3)函数y=+lg(1-tan x)的定义域为________.
[思路点拨] 求定义域时,要注意正切函数自身的限制条件,另外解不等式时要充分利用三角函数的图像或三角函数线.
答案:(1)B (2) (3)
解析:(1)当-<x<0时,-1<tan x<0,∴≤-1;
当0<x<时,0<tan x<1,∴≥1.
即当x∈∪时,函数y=的值域是(-∞,-1)∪(1,+∞).
(2)要使函数有意义应满足-≠kπ+,k∈Z,得x≠-4kπ-,k∈Z,
所以函数的定义域为.
(3)要使函数y=+lg(1-tan x)有意义,则
即-1≤tan x<1.
在上满足上述不等式的x的取值范围是.
又因为y=tan x的周期为π,所以所求x的定义域为.
【反思感悟】
1.求正切函数定义域的方法
(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义即x≠+kπ,k∈Z.
(2)求正切型函数y=Atan(ωx+φ)(A≠0,ω>0)的定义域时,要将“ωx+φ”视为一个“整体”.令ωx+φ≠kπ+,k∈Z,解得x.
2.解形如tan x>a的不等式的步骤
提醒:求定义域时,要注意正切函数自身的限制条件.
【跟踪训练】
1.函数y=tan的定义域是( )
A.
B.
C.
D.
答案:B
解析:由题意tan>0,
即tan<0,
∴kπ-<x-<kπ,
∴kπ-<x<kπ+,k∈Z,故选B.
2.求函数y=tan2+tan+1的定义域和值域.
解:由3x+≠kπ+,k∈Z,得x≠+(k∈Z),
所以函数的定义域为.
设t=tan,
则t∈R,y=t2+t+1=2+≥,
所以原函数的值域是.
题型二 正切函数奇偶性、周期性和图像的对称性
【例2】 (1)函数f(x)=tan的周期为________.
(2)已知函数y=tan,则该函数图像的对称中心坐标为________.
(3)判断下列函数的奇偶性:
①y=3xtan 2x-2x4;②y=cos+tan x.
[思路点拨] (1)形如y=Atan(ωx+φ)(Aω≠0)的周期T=,也可以用定义法求周期.
(2)形如y=Atan(ωx+φ)(Aω≠0)的对称中心横坐标可由ωx+φ=,k∈Z求出.
(3)先求定义域看是否关于原点对称,若对称再判断f(-x)与f(x)的关系.
答案:(1) (2),k∈Z
解析:(1)法一:(定义法)
∵tan=tan,
即tan=tan,
∴f(x)=tan的周期是.
法二:(公式法)
f(x)=tan的周期T=.
(2)由x-=(k∈Z)得x=+(k∈Z),所以图像的对称中心坐标为,k∈Z.]
(3)①定义域为,关于原点对称,
又f(-x)=3(-x)tan 2(-x)-2(-x)4=3xtan 2x-2x4=f(x),所以它是偶函数.
②定义域为,关于原点对称,
y=cos+tan x=sin x+tan x,
又f(-x)=sin(-x)+tan(-x)=-sin x-tan x=-f(x),所以它是奇函数.
【反思感悟】
1.函数f(x)=Atan(ωx+φ)周期的求解方法:
(1)定义法.
(2)公式法:对于函数f(x)=Atan(ωx+φ)的最小正周期T=.
(3)观察法(或图像法):观察函数的图像,看自变量间隔多少,函数值重复出现.
2.判定与正切函数有关的函数奇偶性的方法:
先求函数的定义域,看其定义域是否关于原点对称,若其不关于原点对称,则该函数为非奇非偶函数;若其关于原点对称,再看f(-x)与f(x)的关系.
提醒:y=tan x,x≠kπ+,k∈Z的对称中心坐标为,k∈Z.
【跟踪训练】
3.判断下列函数的奇偶性
(1)f(x)=;
(2)f(x)=tan+tan.
解:(1)由得
f(x)的定义域为,
不关于原点对称,
所以函数f(x)既不是偶函数,也不是奇函数.
(2) 函数定义域为,
关于原点对称,
又f(-x)=tan+tan
=-tan-tan
=-f(x),
所以函数f(x)是奇函数.
题型三 正切函数单调性的应用
[探究问题]
1.正切函数y=tan x在其定义域内是否为增函数?
提示:不是.正切函数的图像被直线x=kπ+(k∈Z)隔开,所以它的单调区间只在(k∈Z)内,而不能说它在定义域内是增函数.假设x1=,x2=π,x1
提示:先根据正切函数的周期性把两角化到同一单调区间内,再由正切函数的单调性进行比较.
【例3】 (1)tan 1,tan 2,tan 3,tan 4从小到大的排列顺序为________.
(2)求函数y=3tan的单调区间.
[思路点拨] (1)利用y=tan x在上为增函数比较大小,注意tan 1=tan(π+1).
(2)先将原函数化为y=-3tan,再由-+kπ<2x-<+kπ,k∈Z,求出单调减区间.
(1) 答案:tan 2<tan 3<tan 4<tan 1
解析:y=tan x在区间上是单调增函数,且tan 1=tan(π+1),
又<2<3<4<π+1<,
所以tan 2<tan 3<tan 4<tan 1.
(2)解:y=3tan=-3tan,
由-+kπ<2x-<+kπ,k∈Z得,
-+π<x<+π,k∈Z,
所以y=3tan的减区间为(-+π,+π),k∈Z.
【多维探究】
1.将本例(2)中的函数改为“y=3tan”,结果又如何?
解:由kπ-
2.将本例(2)中的函数改为“y=lgtan x”结果又如何?
解:因为函数y=lg x在(0,+∞)上为增函数.
所以函数y=lgtan x的单调递增区间
就是函数y=tan x(tan x>0)的递增区间,
即,k∈Z.
【反思感悟】
1.求函数y=Atan(ωx+φ)(A>0,ω≠0,且A,ω,φ都是常数)的单调区间的方法
(1)若ω>0,由于y=tan x在每一个单调区间上都是增函数,故可用“整体代换”的思想,令kπ-<ωx+φ<kπ+,k∈Z,解得x的范围即可.
(2)若ω<0,可利用诱导公式先把y=Atan(ωx+φ)转化为y=Atan[-(-ωx-φ)]=-Atan(-ωx-φ),即把x的系数化为正值,再利用“整体代换”的思想,求得x的范围即可.
2.运用正切函数单调性比较大小的步骤
(1)运用函数的周期性或诱导公式将角化到同一单调区间内.
(2)运用单调性比较大小关系.
提醒:y=Atan(ωx+φ)(A>0,ω>0)只有增区间;y=Atan(ωx+φ)(A<0,ω>0)只有减区间.
五、达标检测
1.思考辨析
(1)正切函数的定义域和值域都是R.( )
(2)正切函数图像是中心对称图形,有无数个对称中心.( )
(3)正切函数图像有无数条对称轴,其对称轴是x=kπ±,k∈Z.( )
(4)正切函数是增函数.( )
答案:(1)× (2)√ (3)× (4)×
2.若tan x≥1,则( )
A.2kπ-<x<2kπ(k∈Z)
B.x≤(2k+1)π(k∈Z)
C.kπ-<x≤kπ(k∈Z)
D.kπ+≤x<kπ+(k∈Z)
答案:D
解析:因为tan x≥1=tan.
所以+kπ≤x<+kπ,k∈Z.
3.求函数y=tan(π-x),x∈的值域为________.
答案:(-,1)
解析:y=tan(π-x)=-tan x,
在上为减函数,
所以值域为(-,1).
4.求函数y=tan的定义域、最小正周期、单调区间及其图像的对称中心.
解:①由-≠kπ+,k∈Z,得x≠2kπ+,k∈Z,
∴函数的定义域为.
②T==2π,
∴函数的最小正周期为2π.
③由kπ-<-<kπ+,k∈Z,得2kπ-<x<2kπ+,k∈Z,
∴函数的单调递增区间为, k∈Z.
④由-=,k∈Z,得x=kπ+,k∈Z,
∴函数图像的对称中心是,k∈Z.
六、本课小结
1.利用单位圆中的正切线作正切函数的图像,作图较为准确,但画图时较繁,我们常用“三点两线”法作正切曲线的简图.
2.正切函数与正弦函数、余弦函数的性质比较.
性质 正切函数 正弦函数、余弦函数
定义域 R
值域 R [-1,1]
最值 无 最大值为1
最小值为-1
单调性 仅有单调递增区间,不存在单调递减区间 单调递增区间、单调递减区间均存在
奇偶性 奇函数 正弦函数是奇函数
余弦函数是偶函数
周期性 T=π T=2π
对称性 有无数个对称中心,不存在对称轴 对称中心和对称轴均有无数个
七、课后作业
1.复习回顾本节内容.
2.完成本节配套课后练习《高一必修三 7.3.4正切函数的性质与图像课时精练(配套)》.
