2021-2022学年北师大版数学八年级下册6.2平行四边形的判定(3)课件(21张)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级下册6.2平行四边形的判定(3)课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 998.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 21:13:55 | ||
图片预览







文档简介
(共21张PPT)
课题:平行四边形判定(3)
学习目标
1.探索并证明平行四边形其他相关的结论,发展演绎能力;
2.利用平行四边形的判定研究“夹在平行线之间的平行线段相等”,并理解平行线之间的距离;
3.能够综合运用平行四边形的判定定理和性质进行计算和证明.
从边来判定
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
从角来判定
两组对角分别相等的四边形是平行四边形.
从对角线来
判定
两条对角线互相平分的四边形是平行四边形.
平行四边形的判定方法
复习导入
在笔直的铁轨上,夹在两根铁轨之间的平行枕木是否一样长?你能说明理由吗?与同伴交流.
思考:
导入新知
如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺度量出平行线之间的垂线段的长度.
经过度量,我们发现这些垂线段的长度都相等 (从图中也可以看到这一点).
猜想:平行线间距离处处相等.
平行线之间的距离
探索新知
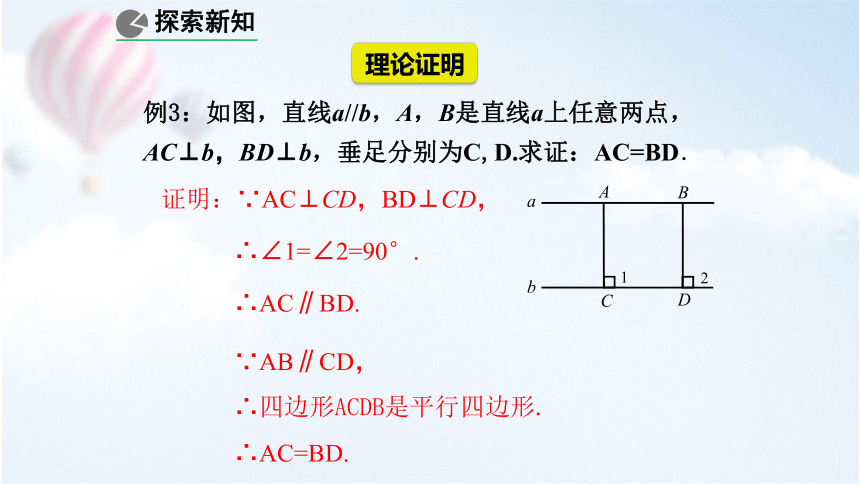
例3:如图,直线a//b,A,B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.求证:AC=BD.
证明:∵AC⊥CD,BD⊥CD,
理论证明
∴∠1=∠2=90°.
∴AC∥BD.
∵AB∥CD,
∴四边形ACDB是平行四边形.
∴AC=BD.
a
b
A
B
C
D
1
2
探索新知
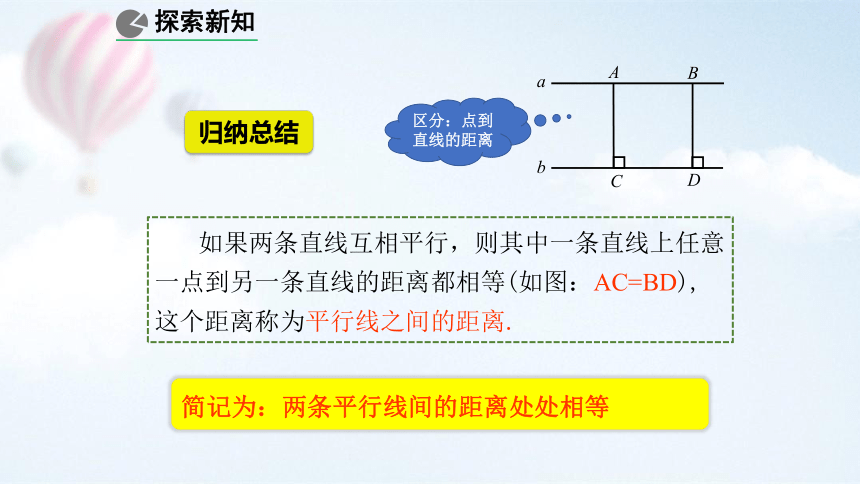
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等(如图:AC=BD),这个距离称为平行线之间的距离.
归纳总结
简记为:两条平行线间的距离处处相等
探索新知
区分:点到直线的距离
a
b
A
B
C
D
1.如图,已知l1∥l2,AB∥CD,HE⊥l2,FG⊥l2,垂足分别为E,G,则下列说法错误的是( )
A.AB的长就是l1与l2之间的距离
B.AB=CD
C.HE的长就是l1与l2之间的距离
D.HE=FG
A
跟踪练习
牛刀小试
2.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( )
A.变大
B.变小
C.不变
D.变大变小要看点P向左
还是向右移动
跟踪练习
牛刀小试
3.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
分析:根据平行线之间的距离处处相等
10
解析:设高为h,则S△ABD= ·BD·h=16,所以h=4,
所以S△ACE= ·AE·h= ×5 ×4=10.
巩固练习
变式训练
讲授新课
例4:已知,如图,在平行四边形ABCD中,BN=DM,BE=DF.求证:四边形MENF是平行四边形.
证明:在平行四边形ABCD中,AD∥BC,
∴∠MDF=∠NBE.
∵DM=BN,DF=BE,
∴△MDF≌△NBE(SAS).
∴MF=NE,∠MFD=∠NEB.
∴四边形MENF是平行四边形.
∴∠MFE=∠NEF ∴FM∥EN.
平行四边形性质与判定的综合运用
二
如图:平行四边形ABCD中,∠ABC=700,∠ABC的平分线交AD于点E,过D作BE的平行线交BC于点F,求∠CDF的度数.
35°
35°
35°
110°
110°
35°
方法1:
平行线的性质
方法2:
巩固练习
2.如图,在平行四边形ABCD中,E,F分别是边CD和AB上的点,AE//CF,BE交CF于点H,DF交AE于点G.求证:EG=FH
变式训练
巩固练习
□AFCE
□BEDF
□FHEG
BF∥DE,BF=DE
DF∥BE,AE=FC
EG=FH
1.(1)在□ABCD中,∠A =150,AB=8cm,BC=10cm,
则S□ABCD = .
提示:过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.
40cm2
(2)若点P是□ABCD上AD上任意一点,那么△PBC的面积是 .
20cm2
提示:△PBC与□ABCD是同底等高.
课堂检测
基础巩固题
能力提升题
课堂检测
2.如图,在平行四边形ABCD中,E,F分别是边CD和AB上的点,AE=CF,
M,N分别是DE和BF的中点.求证:四边形ENFM是平行四边形
平行四边形
五种判定方法
对边平行,对边相等,对角相等
判定
性质
夹在两条平行线间的平行线段处处相等
课堂小结
谈谈你的收获与思考
如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向点D以1 cm/s的速度运动,到点D即停止,点Q自点C向点B以2cm/s的速度运动,到点B即停止,直线PQ截梯形成两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?
拓广探索题
课堂检测
谢谢!
2.如图,已知l1∥l2∥l3,相邻两条平行直线间的距离都等于1.若等腰直角三角形ABC的三个顶点分别在这三条平行直线上,求斜边AB的长.
能力提升题
课堂检测
分析:利用平行线间的距离相等构造全等三角形,然后利用勾股定理求AB的长.
解:如图,过点A作AD⊥l1于点D,过点B作BE⊥l1于点E.
∵∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE.
在△ACD和△CBE中,∠CAD=∠BCE,
∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS).
∴CD=BE=1.
解:设点P,Q同时出发t s后四边形PDCQ或四边形APQB是平行四边形,根据已知得到AP=t,PD=24-t,CQ=2t,BQ=30-2t.
①若四边形PDCQ是平行四边形,则PD=CQ,∴24-t=2t,∴t=8,∴8 s后四边形PDCQ是平行四边形;
②若四边形APQB是平行四边形,则AP=BQ,∴t=30-2t,∴t=10,∴10 s后四边形APQB是平行四边形
课题:平行四边形判定(3)
学习目标
1.探索并证明平行四边形其他相关的结论,发展演绎能力;
2.利用平行四边形的判定研究“夹在平行线之间的平行线段相等”,并理解平行线之间的距离;
3.能够综合运用平行四边形的判定定理和性质进行计算和证明.
从边来判定
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
从角来判定
两组对角分别相等的四边形是平行四边形.
从对角线来
判定
两条对角线互相平分的四边形是平行四边形.
平行四边形的判定方法
复习导入
在笔直的铁轨上,夹在两根铁轨之间的平行枕木是否一样长?你能说明理由吗?与同伴交流.
思考:
导入新知
如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺度量出平行线之间的垂线段的长度.
经过度量,我们发现这些垂线段的长度都相等 (从图中也可以看到这一点).
猜想:平行线间距离处处相等.
平行线之间的距离
探索新知
例3:如图,直线a//b,A,B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.求证:AC=BD.
证明:∵AC⊥CD,BD⊥CD,
理论证明
∴∠1=∠2=90°.
∴AC∥BD.
∵AB∥CD,
∴四边形ACDB是平行四边形.
∴AC=BD.
a
b
A
B
C
D
1
2
探索新知
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等(如图:AC=BD),这个距离称为平行线之间的距离.
归纳总结
简记为:两条平行线间的距离处处相等
探索新知
区分:点到直线的距离
a
b
A
B
C
D
1.如图,已知l1∥l2,AB∥CD,HE⊥l2,FG⊥l2,垂足分别为E,G,则下列说法错误的是( )
A.AB的长就是l1与l2之间的距离
B.AB=CD
C.HE的长就是l1与l2之间的距离
D.HE=FG
A
跟踪练习
牛刀小试
2.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( )
A.变大
B.变小
C.不变
D.变大变小要看点P向左
还是向右移动
跟踪练习
牛刀小试
3.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
分析:根据平行线之间的距离处处相等
10
解析:设高为h,则S△ABD= ·BD·h=16,所以h=4,
所以S△ACE= ·AE·h= ×5 ×4=10.
巩固练习
变式训练
讲授新课
例4:已知,如图,在平行四边形ABCD中,BN=DM,BE=DF.求证:四边形MENF是平行四边形.
证明:在平行四边形ABCD中,AD∥BC,
∴∠MDF=∠NBE.
∵DM=BN,DF=BE,
∴△MDF≌△NBE(SAS).
∴MF=NE,∠MFD=∠NEB.
∴四边形MENF是平行四边形.
∴∠MFE=∠NEF ∴FM∥EN.
平行四边形性质与判定的综合运用
二
如图:平行四边形ABCD中,∠ABC=700,∠ABC的平分线交AD于点E,过D作BE的平行线交BC于点F,求∠CDF的度数.
35°
35°
35°
110°
110°
35°
方法1:
平行线的性质
方法2:
巩固练习
2.如图,在平行四边形ABCD中,E,F分别是边CD和AB上的点,AE//CF,BE交CF于点H,DF交AE于点G.求证:EG=FH
变式训练
巩固练习
□AFCE
□BEDF
□FHEG
BF∥DE,BF=DE
DF∥BE,AE=FC
EG=FH
1.(1)在□ABCD中,∠A =150,AB=8cm,BC=10cm,
则S□ABCD = .
提示:过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.
40cm2
(2)若点P是□ABCD上AD上任意一点,那么△PBC的面积是 .
20cm2
提示:△PBC与□ABCD是同底等高.
课堂检测
基础巩固题
能力提升题
课堂检测
2.如图,在平行四边形ABCD中,E,F分别是边CD和AB上的点,AE=CF,
M,N分别是DE和BF的中点.求证:四边形ENFM是平行四边形
平行四边形
五种判定方法
对边平行,对边相等,对角相等
判定
性质
夹在两条平行线间的平行线段处处相等
课堂小结
谈谈你的收获与思考
如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向点D以1 cm/s的速度运动,到点D即停止,点Q自点C向点B以2cm/s的速度运动,到点B即停止,直线PQ截梯形成两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?
拓广探索题
课堂检测
谢谢!
2.如图,已知l1∥l2∥l3,相邻两条平行直线间的距离都等于1.若等腰直角三角形ABC的三个顶点分别在这三条平行直线上,求斜边AB的长.
能力提升题
课堂检测
分析:利用平行线间的距离相等构造全等三角形,然后利用勾股定理求AB的长.
解:如图,过点A作AD⊥l1于点D,过点B作BE⊥l1于点E.
∵∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE.
在△ACD和△CBE中,∠CAD=∠BCE,
∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS).
∴CD=BE=1.
解:设点P,Q同时出发t s后四边形PDCQ或四边形APQB是平行四边形,根据已知得到AP=t,PD=24-t,CQ=2t,BQ=30-2t.
①若四边形PDCQ是平行四边形,则PD=CQ,∴24-t=2t,∴t=8,∴8 s后四边形PDCQ是平行四边形;
②若四边形APQB是平行四边形,则AP=BQ,∴t=30-2t,∴t=10,∴10 s后四边形APQB是平行四边形
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
