2021-2022学年北师大版数学八年级下册6.3三角形中位线课件(18张)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级下册6.3三角形中位线课件(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 825.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 21:17:09 | ||
图片预览


文档简介
(共18张PPT)
课题:三角形的中位线
B
C
A
回顾旧知
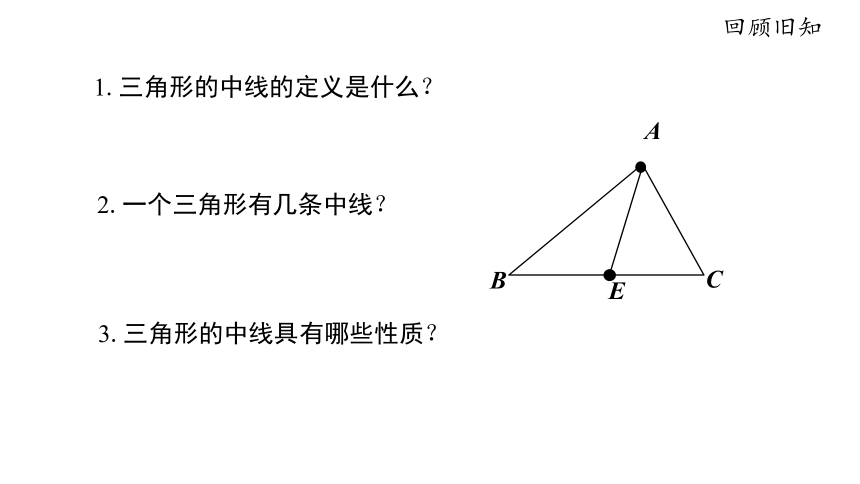
1.三角形的中线的定义是什么?
2.一个三角形有几条中线?
3.三角形的中线具有哪些性质?
E
引入新知
A
B
C
D
E
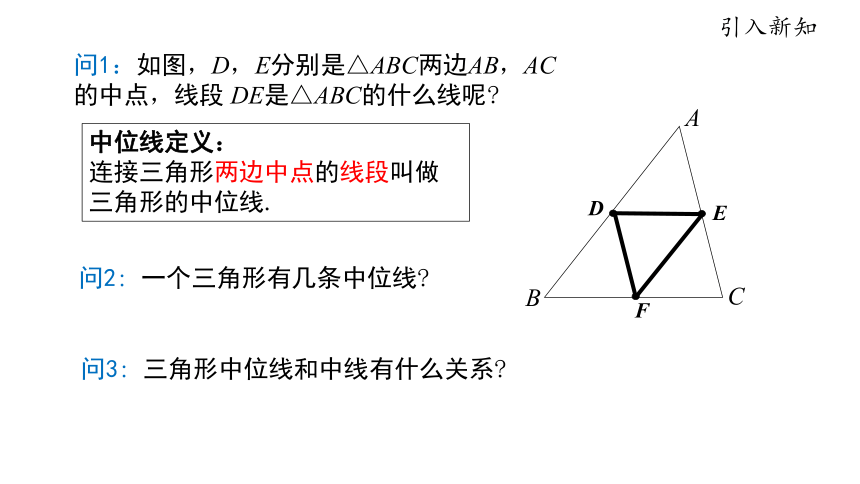
中位线定义:
连接三角形两边中点的线段叫做三角形的中位线.
问2: 一个三角形有几条中位线
问1:如图,D,E分别是△ABC两边AB,AC 的中点,线段 DE是△ABC的什么线呢
问3: 三角形中位线和中线有什么关系
F
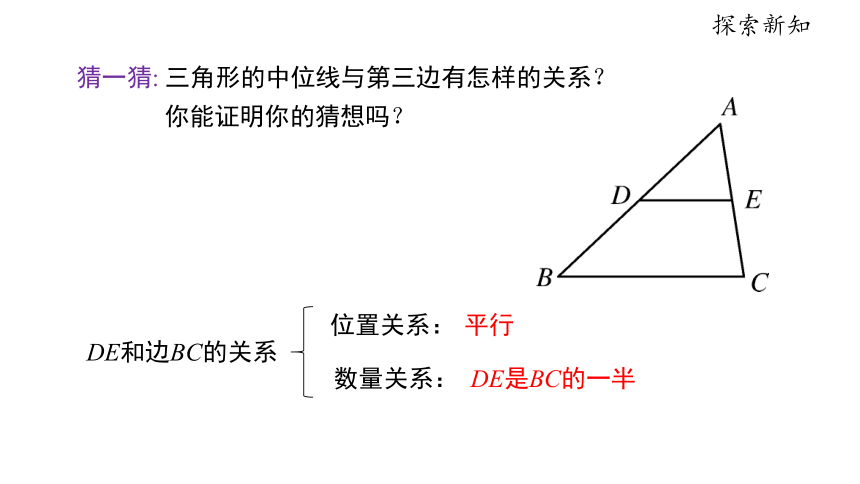
猜一猜: 三角形的中位线与第三边有怎样的关系?
你能证明你的猜想吗?
探索新知
DE和边BC的关系
数量关系:
位置关系:
平行
DE是BC的一半
方法一:测量法
探索新知
测量:
⑴∠ADE,∠ABC度数.
⑵ DE,BC 长度.
测量结果:∠ADE=∠ABC, DE= BC.
结论:DE∥BC, DE=BC.
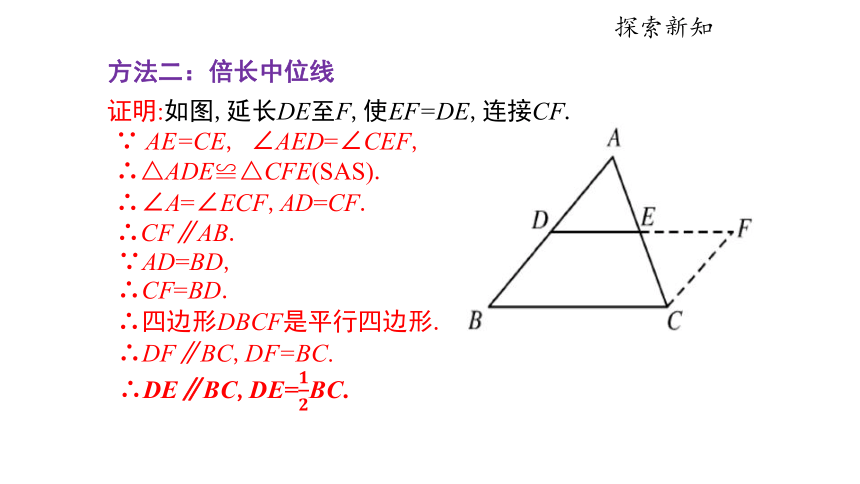
方法二:倍长中位线
探索新知
证明:如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE, ∠AED=∠CEF,
∴△ADE≌△CFE(SAS).
∴∠A=∠ECF,AD=CF.
∴CF∥AB.
∵AD=BD,
∴四边形DBCF是平行四边形.
∴CF=BD.
∴DE∥BC,DE=BC.
∴DF∥BC,DF=BC.
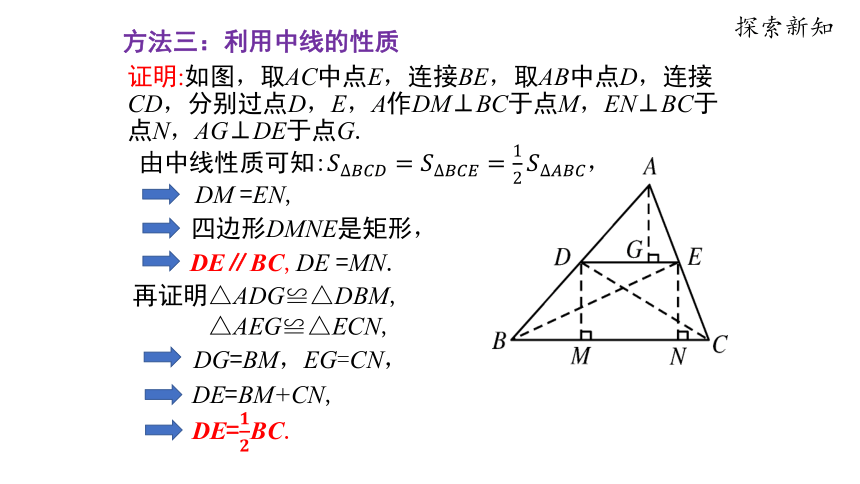
方法三:利用中线的性质
探索新知
证明:如图,取AC中点E,连接BE,取AB中点D,连接CD,分别过点D,E,A作DM⊥BC于点M,EN⊥BC于点N,AG⊥DE于点G.
由中线性质可知:,
DM =EN,
四边形DMNE是矩形,
DE∥BC,DE =MN.
再证明△ADG≌△DBM,
△AEG≌△ECN,
DG=BM,EG=CN,
DE=BM+CN,
DE=BC.
探索新知
证明: 如图,以点B为坐标原点、BC所在的直线为x轴建立平面直角坐标系.
方法四:利用坐标系进行证明
设A( m,n) ,C( x,0),
根据中点公式可知,
D( ,) ,E( ,),
DE∥BC,
DE= ,
DE = BC.
探索新知
方法五:割补法
如图,在我国古代数学名著《九章算术》中,刘徽通过割补的方法推导三角形面积公式,从三角形面积公式的推导过程中也能得到三角形中位线定理.
三角形中位线定理:
三角形的中位线平行于第三边,且等于第三边的一半.
用符号语言表示:
∵DE是△ABC的中位线,
∴DE∥BC,
探索新知
探索新知
如图,已知D,E,F分别是AB,AC,BC的中点,连接DE,DF,EF.
问:(1)图中有几个平行四边形
(2)△ABC的中位线分成的四个三角形形状、大小有什么关系
它们的周长和面积与原三角形的周长和面积又有什么关系
思考:
三角形的一条中位线与第三边上中线互相平分.
解:
(1)图中有3个平行四边形.它们分别是
□ADFE, □DBFE, □DFCE.
(2)由平行四边形的性质可知,
△ADE≌△FED,
△DBF≌△FED,
△EFC≌△FED.
△ADE≌△FED≌△EFC≌△DBF.
(2),,分别是,,的中点,,,分别是,,的中点,依此类推,若△ABC的周长为a,面积为S,则△的周长多少?面积多少?
例题精讲
例1 如图,在△ABC中,,,分别是边BC,AC,AB的中点.
(1)若△ABC的周长为24,面积为20,则△的周长多少?面积多少?
周长为12,面积为5.
,
.
……
.
,
,
,
……
例2 如图,在平面内任意画一个四边形ABCD,以四边的中点为顶点组成一个新四边形EFGH,这个新四边形是什么四边形 请证明你的结论.
例题精讲
做法一:连一条对角线.
解:四边形EFGH是平行四边形.理由如下:
连接BD,
∴EF∥HG, EF = HG.
∴四边形EFGH是平行四边形.
在△DBC中,
∵H,G分别是DC,BC的中点,
∴HG是△DBC的中位线.
∴HG∥BD, HG = BD.
在△ABD中,
∵E,F分别是AD,AB的中点,
∴EF是△ABD的中位线.
∴EF∥BD, EF = BD.
例题精讲
做法二:连两条对角线.
四边形EFGH是平行四边形.
EF∥BD,
HG∥BD.
HG∥EF.
EH∥AC,
FG∥AC.
EH∥FG.
①位置关系
②数量关系
EF = BD,
HG = BD.
HG =EF.
EH =,
FG = .
EH =FG.
四边形EFGH是平行四边形.
例题精讲
变式训练1
如图,在四边形ABCD中,E,F,G,H分别是AB,CD,AC,BD的中点,四边形GEHF是平行四边形吗 请证明你的结论.
例题精讲
变式训练2
如图,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,延长BA,CD分别交直线EF于M,N.猜想∠AMF与∠DNF的关系,并证明你的结论.
G
GF∥CD,
∠EFG=∠DNF.
EG∥AB,
∠FEG=∠AMF.
GF = CD,
EG = ,
GF=EG.
∠EFG=∠FEG.
∠AMF=∠DNF.
∠AMF=∠DNF.
课堂小结
三角形的中位线
定 义
连结三角形两边中点的线段叫做三角形的中位线.
性质
三角形的中位线平行于第三边,且等于第三边的一半.
应用
①周长;
②面积;
③综合应用.
可持续发展
如图,在△ABC中,AB=AC,延长AB到点D,使BD=AB,E为AB中点,连接CE,CD.
求证:CD=2EC.
课题:三角形的中位线
B
C
A
回顾旧知
1.三角形的中线的定义是什么?
2.一个三角形有几条中线?
3.三角形的中线具有哪些性质?
E
引入新知
A
B
C
D
E
中位线定义:
连接三角形两边中点的线段叫做三角形的中位线.
问2: 一个三角形有几条中位线
问1:如图,D,E分别是△ABC两边AB,AC 的中点,线段 DE是△ABC的什么线呢
问3: 三角形中位线和中线有什么关系
F
猜一猜: 三角形的中位线与第三边有怎样的关系?
你能证明你的猜想吗?
探索新知
DE和边BC的关系
数量关系:
位置关系:
平行
DE是BC的一半
方法一:测量法
探索新知
测量:
⑴∠ADE,∠ABC度数.
⑵ DE,BC 长度.
测量结果:∠ADE=∠ABC, DE= BC.
结论:DE∥BC, DE=BC.
方法二:倍长中位线
探索新知
证明:如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE, ∠AED=∠CEF,
∴△ADE≌△CFE(SAS).
∴∠A=∠ECF,AD=CF.
∴CF∥AB.
∵AD=BD,
∴四边形DBCF是平行四边形.
∴CF=BD.
∴DE∥BC,DE=BC.
∴DF∥BC,DF=BC.
方法三:利用中线的性质
探索新知
证明:如图,取AC中点E,连接BE,取AB中点D,连接CD,分别过点D,E,A作DM⊥BC于点M,EN⊥BC于点N,AG⊥DE于点G.
由中线性质可知:,
DM =EN,
四边形DMNE是矩形,
DE∥BC,DE =MN.
再证明△ADG≌△DBM,
△AEG≌△ECN,
DG=BM,EG=CN,
DE=BM+CN,
DE=BC.
探索新知
证明: 如图,以点B为坐标原点、BC所在的直线为x轴建立平面直角坐标系.
方法四:利用坐标系进行证明
设A( m,n) ,C( x,0),
根据中点公式可知,
D( ,) ,E( ,),
DE∥BC,
DE= ,
DE = BC.
探索新知
方法五:割补法
如图,在我国古代数学名著《九章算术》中,刘徽通过割补的方法推导三角形面积公式,从三角形面积公式的推导过程中也能得到三角形中位线定理.
三角形中位线定理:
三角形的中位线平行于第三边,且等于第三边的一半.
用符号语言表示:
∵DE是△ABC的中位线,
∴DE∥BC,
探索新知
探索新知
如图,已知D,E,F分别是AB,AC,BC的中点,连接DE,DF,EF.
问:(1)图中有几个平行四边形
(2)△ABC的中位线分成的四个三角形形状、大小有什么关系
它们的周长和面积与原三角形的周长和面积又有什么关系
思考:
三角形的一条中位线与第三边上中线互相平分.
解:
(1)图中有3个平行四边形.它们分别是
□ADFE, □DBFE, □DFCE.
(2)由平行四边形的性质可知,
△ADE≌△FED,
△DBF≌△FED,
△EFC≌△FED.
△ADE≌△FED≌△EFC≌△DBF.
(2),,分别是,,的中点,,,分别是,,的中点,依此类推,若△ABC的周长为a,面积为S,则△的周长多少?面积多少?
例题精讲
例1 如图,在△ABC中,,,分别是边BC,AC,AB的中点.
(1)若△ABC的周长为24,面积为20,则△的周长多少?面积多少?
周长为12,面积为5.
,
.
……
.
,
,
,
……
例2 如图,在平面内任意画一个四边形ABCD,以四边的中点为顶点组成一个新四边形EFGH,这个新四边形是什么四边形 请证明你的结论.
例题精讲
做法一:连一条对角线.
解:四边形EFGH是平行四边形.理由如下:
连接BD,
∴EF∥HG, EF = HG.
∴四边形EFGH是平行四边形.
在△DBC中,
∵H,G分别是DC,BC的中点,
∴HG是△DBC的中位线.
∴HG∥BD, HG = BD.
在△ABD中,
∵E,F分别是AD,AB的中点,
∴EF是△ABD的中位线.
∴EF∥BD, EF = BD.
例题精讲
做法二:连两条对角线.
四边形EFGH是平行四边形.
EF∥BD,
HG∥BD.
HG∥EF.
EH∥AC,
FG∥AC.
EH∥FG.
①位置关系
②数量关系
EF = BD,
HG = BD.
HG =EF.
EH =,
FG = .
EH =FG.
四边形EFGH是平行四边形.
例题精讲
变式训练1
如图,在四边形ABCD中,E,F,G,H分别是AB,CD,AC,BD的中点,四边形GEHF是平行四边形吗 请证明你的结论.
例题精讲
变式训练2
如图,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,延长BA,CD分别交直线EF于M,N.猜想∠AMF与∠DNF的关系,并证明你的结论.
G
GF∥CD,
∠EFG=∠DNF.
EG∥AB,
∠FEG=∠AMF.
GF = CD,
EG = ,
GF=EG.
∠EFG=∠FEG.
∠AMF=∠DNF.
∠AMF=∠DNF.
课堂小结
三角形的中位线
定 义
连结三角形两边中点的线段叫做三角形的中位线.
性质
三角形的中位线平行于第三边,且等于第三边的一半.
应用
①周长;
②面积;
③综合应用.
可持续发展
如图,在△ABC中,AB=AC,延长AB到点D,使BD=AB,E为AB中点,连接CE,CD.
求证:CD=2EC.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
