猜想与反驳

课件40张PPT。 猜想与反驳数学思维方法2012.8 猜想与反驳
数学问题的提出和解决是推动数学发展的重要力量。猜想与反驳是解决数学问题的一个重要思想方法。猜想是人们根据一定的经验材料和已知事实对数学问题作出的推测性判断，可能为真，也可能为假。对于猜想得到的命题，或者经过演绎证明确认为真命题，或者举出反例判断其为假命题。用一个反例作为论据否定猜想的方法称为反例反驳。归纳猜想和类比猜想是数学猜想的两种主要类型。在数学教学中，加强猜想能力培养对于提高学生的思维能力和创造能力具有重要意义。 第一节 归纳猜想
一、归纳
归纳法是通过一些个别的、特殊的情况加以观察、分析，进而导出一个一般性结论的推理方法。归纳法是一种从特殊到一般的推理方法，它与演绎法被认为是理性思维中两种最重要的推理方法。 二、归纳的类型
1、不完全归纳法
所谓不完全归纳法，是根据对某类事物中的部分对象的分析，作出关于该类事物的一般性结论的推理方法。
不完全归纳法的一般推理形式是： 例3 用1到8这8个数字分别组成两个四位数，使他们相乘的积最大。请写出这两个数。例2 求凸n边形的内角和公式。 分析：由已知的八个数字组成两个四位数，可以有很多种不同的方法，欲通过逐一列举的方法进行比较积的大小，显然相当复杂。不妨先解决一个比较简单而又不改变原命题性质的问题：用5，6，7，8这四个数字组成两个两位数，使其乘积最大。易知，十位数字应取较大的两个数8和7，这样得到的两位数只有 85，76和 86，75两种情况。显然 85 *76＞86 * 75。进一步分析上述不等式的真正含义，可以揭示出数字组合与其乘积之间的联系。无论85，76还是86，75，它们的和都相等，只是前一对数比后一对数更为接近。 由此可以归纳出两条组数的原则：
①较大的数字尽量靠左；
②要加上的两个数字，其中较大的应附在较小的
后面，使得所组成的两数之差较小。
根据上述原则就可逐步写出所求的四位数：
85 853 8531
7 76 764 7642
故所求的四位数是8531，7642。 值得指出的是，不完全归纳法具有一定的局限性。从不完全归纳法的含义中可以看到，不完全归纳法的结果是在仅仅观察、分析了某类事物的部分对象之后，对该类事物的属性所提出的猜想。因此，其前提与结论之间不具有必然的联系，其结果具有或然性。不完全归纳法只是一种合情推理，而不是严格的逻辑论证方法，所得结论的正确性，尚需经过严格的逻辑推理和实践检验后才能确认。 2、完全归纳法
完全归纳法是根据对某类事物中的每一对象的情况分析，进而作出关于该类事物的一般性结论的推理方法。
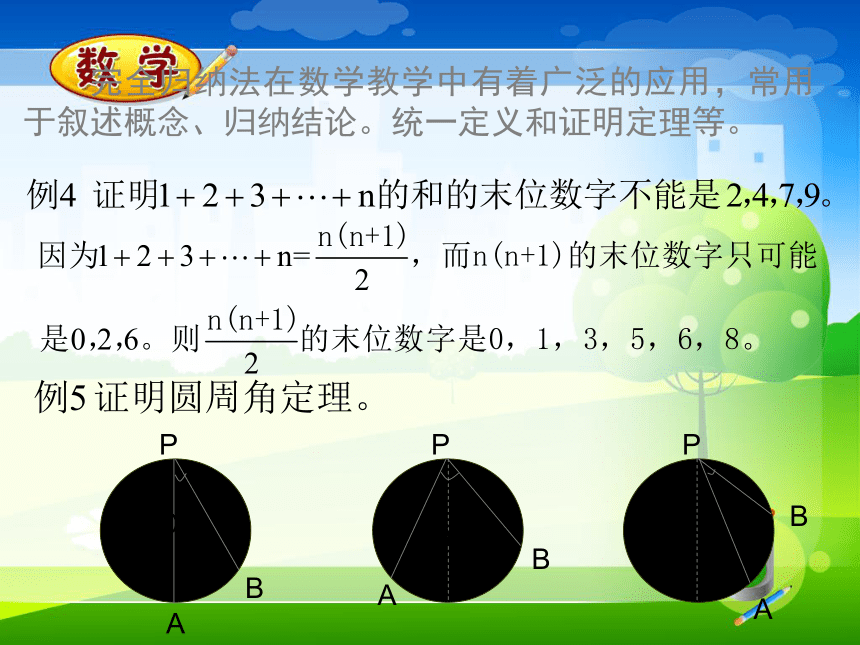
完全归纳法的一般推理形式是： 完全归纳法在数学教学中有着广泛的应用，常用于叙述概念、归纳结论。统一定义和证明定理等。 三、归纳猜想
1、数学猜想
综观数学发展的历史，数学问题的产生主要来自三个方面：
（1）人们的社会实践
（2）自然科学的刺激
（3）数学内部的需要
2、归纳猜想
人们运用归纳法，得出对一类现象的某种一般性认识的一种推测性的判断，即猜想，这种思想方法称为归纳猜想。 将完全归纳法与不完全归纳法进行比较，我们可以知道：由完全归纳法得出的结论是可靠的，具有确定性。因此，完全归纳法可以作为一种严格的论证方法。这是因为完全归纳法考察了某类事物的全体对象，因此，当它的前提为真时，其结论必然为真。而演绎推理是前提与结论之间有必然联系的推理，即当前提为真时，结论必为真。所以，完全归纳法实质上属于演绎推理的范畴。 分析：10阶方阵一共有100个数，举出一个实例比较繁，不妨先研究一个2X2的方阵，
显然，用后一种方法选出来的数大。因为四个数中某些数可以相同，所以有理由猜想，在 10 X 10的方阵中，用前一种方法选省来的数不大于用后一种方法选出来的数。这个猜想的数学表示是： 归纳猜想的思维步骤为：特例---归纳---猜想。面对一个数学猜想，我们可以从两个方向进行思考：
通过演绎推理证由此猜想为真;
或者找出反例说由此猜想为假，从而否定或修正此猜想。 第二节 类比猜想
一、类比
所谓类比，是指由一类事物所具有的某种属性，可以推测与其类似的事物也具有这种属性的一种推理方法。常称这种方法为类比法，也称类比推理。波利亚认为“类比就是一种相似”。类比法是一种从特殊到特殊的推理方法，其结论具有或然性，是否正确需要经过严格的证明或者实践检验。开普勒说：“我珍视类比胜过任何别的东西。它是我最信赖的老师，它能揭示自然界的秘密，在几何学中它是最不容易忽视的。”拉普拉斯指出：“甚至在数学里，发现真理的主要工具也是归纳和类比。” 二、类比的类型
1、表层类比（形式或结构上的简单类比）
表层类比是根据两个被比较对象的表面形式或结构上的相似所进行的类比。这种类比可靠性较差，结论具有很大的或然性。
如a(b+c)=ab+ac类比出sin(A+B)=sinA+sinB是错误的；而类比到数列的和的极限（分别存在时）是正确的。
又如，由三角形内角平分线性质，类比得到三角形外角平分线性质，就是一种结构上的类比。 2、深层类比（方法或模式上的纵向类比）
深层类比又称实质性类比。它是通过对被比较对象的处于相互依存的各种相似属性之间的多种因果关系的分析而得到的类比。这种纵向类比，是在数学的同一分支内的一种类比。一般表现为空间问题用平面问题来类比，即降维类比；多元问题用一元问题来类比，即减元类比等。
例如，平面上的一个三角形可与空间的一个四面体作类比。从平面勾股定理可类比出空间勾股定理。即 3、沟通类比（各分科之间的类比）
这种类比与深层类比的主要区别是。深层类化所类比的方法或模式是比较简单的模仿，不如沟通类比深刻；沟通类比所涉及的对象之间的类比往往不是一眼就能发现的，要经过适当的联想才能进行。
类比推理在小学数学学习中亦有着广泛的应用，它是学生获取新的数学知识的主要方法之一。例如，由加法对乘法的分配律，通过类比可以得到减法对乘法的分配律；由整数、小数乘法的算法，运用类比可推出分数乘法的算法。又如，在求解问题时，可以运用波利亚提出的“选一个类似的、较易的问题，去解决它，改造它的解法，以便把他作为一个模式。然后，利用刚刚建立的模式，以达到原来问题的解法。” 三、类比猜想
人们运用类比法，根据一类事物所具有的某种属性，得出与其类似的事物也具有这种属性的一种推测性的判断，即猜想，这种思想方法称为类比猜想。
例如，分式与分数非常相似，只不过是用字母替代数而已＿因此，我们可以猜想，分式与分数在定义、基本性质、约分、通分。四则运算等方面都是对应相似的。事实也确是如此。 尽管类比法有着广泛的应用，但是它毕竟是一种合情推理，由类比得出的正确结论虽然很多，可是由类比导出的错误结论也不少见。因此，类比得到的结论正确与否，还必须经过严格的证明。
例如，在立体几何中，常常会遇到一些与平面几何中“形式”相同的命题：
①不相交的两直线一定平行；
②垂直于同一直线的两直线一定平行；
③过已知点作已知直线的垂线，有且只有一条。
这些在平面几何中的真命题，在立体几何中却都是假命题。 例3正方形ABCD中，E、F分别为AB、BC的中点，CE与DF交于P点，求证：AP=AD。分析：即证角ADP=角APD，而角ADF=DEA，故只需证明A、E、P、D四点共圆。思考：已知C点在圆O直径BE的延长线上，CA切圆O于A点，DC是角ACB的平分线交AE于F，交AB于D点。
（1）求角ADF的度数：
（2）若AB=AC，求AC：BC。 第三节 反例反驳
一、反例反驳
提出一个问题的猜想是解决这个问题过程中的一个重要步骤，但并不是解决问题的终结。人们提出的猜想总是有两种可能：命题为真或者命题为假。因此：或者给出证明；或者加以反驳。在数学中，反驳通常都是寻找一个符合猜想条件的特例。这个特例称为此猜想的反例。这种用一个反例作为论据否定猜想的方法就叫做反例反驳。它是用特殊否定一般的一种思维形式。 反例反驳在逻辑上的依据是：如果命题成立，则命题应该对一切特例都成立；既然现在这个作为反例的特例与命题矛盾，因此这个命题不成立。由此可知，否定一个猜想的反例应该具备如下两个条件：
①反例满足构成猜想的所有条件；
②反例与构成猜想的结论矛盾。 二、反例在数学发展中的应用
如果在已有的数学理论体系中发现了反例，而这个反例既不能被已有的理论所解释，又无法从已有的理论框架中排除，这就形成了悻论。虽然数学悻论不会经常出现，但是一旦出现，就能深刻揭示出数学体系内部隐藏的矛盾，引发出一系列的重大问题，从而促进数学理论的完善、更新和发展。
第三次数学危机，是由于在康托尔的一般集合论的边缘发现的悻论所造成的。因为众多数学分支都是建立在集合论的基础上，所以集合论中发现停论自然会引起数学的整个基本结构的有效性的怀疑。 第三次数学危机从整体看来至今尚未解决到令人满意的程度。可是，数学仍然在大踏步地向前发展，数学对人类正在作出越来越大的贡献。正如著名数学哲学家拉卡托斯在《证明与反驳》一书中提出的：数学知识是如何增长的？是靠一成不变地增加千真万确的定理数目，还是按证明与反驳的逻辑不断改进？拉卡托斯的回答是后者。数学发展绝不是一往无前的和平建设，矛盾和冲突充斥了数学发展的历史，今日暂时的大统一源于昨日的大混战。人们在实践中，揭示矛盾，提出猜想，以证明与反驳互为印证协同作用于数学知识的革新与发展。 三、反例在数学中的应用
反例不但在数学的发展史上占有重要的地位，而且在数学教学中也有着极为重要的意义。由于反例在否定一个命题时具有特殊的威力，如能在教学中恰当地加以运用，常常可以收到事半功倍的效果。反倒在数学教学中的应用大致有以下几个方面。
1．在评判学生对提问的回答或批改作业时，可用举反例的方法指出其中的错误。 2．在概念教学中，对某些重要概念，有时单从正面给出定义并举例说明是不够的，为了加深学生对概念本质属性的理解，可以针对学生错误理解的例子，举出反倒让学生辨析。 3．在定理、法则学习中，初学者往往因为死记结论或者错误类比，不注意定理、法则的条件，而常常出错。运用反例可以有效地纠正这类错误。 针对这类错误，可以启发学生对x,y赋值计算，并比较两边的数是否相等。这种具体的反例不仅能使学生认识到错误，而且往往会留下比较深刻的印象。第四节 猜想能力的培养 面对一个问题，经过认真的观察和思考，通过归纳或者类比提出猜想，然后从两个方面入手：演绎证明此猜想为真；或者寻找反例说明此猜想为假，并且进一步修正或者否定此猜想。这两个方向上的工作是相反相成、相互启发、相互制约的。演绎证明即使未能确认猜想为真，所获得的部分结果也能使寻找反例的范围更加明确；举反例则能揭示猜想的不合理部分，有助于对猜想的修正和继续证明。这种从演绎证明和举反例两个方向上去逐步解决问题的方法是科学研究的常用方法之一。数学教学中应当引导学生学习和运用这种方法，这对激发学生的创新精神、培养学生的创造能力会有很大帮助。正是基于这种认识，著名数学教育家波利亚早在1953年就发出呼吁：让我们教猜想吧！ 一、用猜想学习新的知识 学生在学习“能被3整除的数的特征”时，很容易受能被2，5整除的数的特征影响，作出“个位是3的倍数的数能被3整除”的猜想。对此，老师不必急于否定学生的猜想，可出示一列数引导学生进行观察、验证：116，43，253，146，89，259；学生能够发现这6个数的个位数都是3的倍数，但是它们都不能被3整除，从而意识到原先的猜想是错误的，心中充满疑惑，探求新知的强烈欲望会油然而生。 这时老师宜抓住契机写出第二列数：12，21，36，63，234，423，135，531 ；引导学生进行仔细观察，并思考问题：第二列数能否被3整除？这8个数的个位数有什么特点？接着指出：判断一个数能否被3整除不能只看个位，也与数的排列顺序无关。那么，究竟与什么有关，具有什么样的特征呢？在教师的启发下，学生会重新作出下列猜想：①可能与各位数的乘积有关；②可能与各位数的和有关；③可能与各位数的差（大数减小数）有关等。对这些猜想，教师可放手让学生自己进行验证，从而逐步得出能被3整除的数的特征是：一个数的各位上的数字之和能被3整除，这个数就能被3整除。 学生观察后可得出：
小正方形面积的2倍＜圆面积＜小正方形面积的4倍；
即 半径*半径*2＜圆面积＜半径*半径*4。
从而大胆猜想：圆面积大约是半径平方的3倍。教师可在此基础上进一步启发学生结合圆周长计算公式得出猜想：圆的面积是半径平方的ス倍。最后再组织学生通过实验进行验证，由此确认清猜想得到的圆面积公式。 二、用猜想探究数学规律 本题是古埃及数学中一个未经确认真假的命题。因此，我们应做好两种准备：或者证明它正确而加以接受；或者举出反例加以否定，并进一步研究如何修改该命题使之成为正确的命题。
为了研究如何对原来的命题进行修正，需要考虑该命题可能成立的范围。根据分类思想，可将四边形按边、角的特殊性依次分为正方形、矩形、平行四边形、梯形、一般四边形。然后依次对前四种特殊情况进行尝试（因为对一般四边形命题已被否定）。根据举例验证，发现在正方形和矩形中，这个命题是正确的；在平行四边形和梯形中，这个命题不成立。因此猜测这个命题成立的范围是矩形，而且仅仅是矩形。（证略 ）将正三角形与正四面体进行类比，可得到如下猜想：
正四面体内任一点到四个面的距离之和为一定值。 如何证明这个猜想呢？对维维阿尼定理的证明。可通过计算原三角形ABC的面积以及面PAB，面PBC，面PCA三个小三角形的面积而取得成功，其定值恰好为正三角形的高。如右图所示。这种证法称为“面积法”。根据类比推理，我们有理由猜想，使用“体积法”也能证明上述猜想。思考：你站在教室里的任一点到四面的距离之和总为定值？三、用猜想帮助解题 首先用归纳法进行试验：2＋10＝12，2＋14＝16，质数 2不合要求；3＋10＝13，3＋14＝17，质数 3符合要求；5＋10＝15，5＋14＝19，质数 5不合要求；7＋10＝17，7＋14＝21，质数 7不合要求；11＋10＝21，11＋14二25，质数11不合要求；17＋10＝27，17＋14=31，质数 17不合要求；53＋10＝63，53＋14二 67，质数 53不合要求。归纳上述试验，可以建立猜想：符合要求的质数只有3。即除3以外的其他质数分别加上10和14不能都是质数。 因为质数的变化规律相当复杂，不可能用解析式把它表示出来。倘若能够证明除3以外所有自然数分别加上10和14不能都是质数，也就证明了除3以外的所有质数分别加上10和14不能都是质数。为此，可把自然数分成三类：3n，3n＋l，3n十2（n为正整数）。
因为
（3 n＋l）＋14 = 3 n＋15=3（n＋5）是合数，
（3n＋2）＋10=3n＋12=3（n＋4）是合数，
因此，在 3n＋l和 3n＋2这两类自然数中的质数都不符合要求。所以，符合要求的质数只有3。