2021-2022学年北师大版九年级数学下册3.8圆内接正多边形同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.8圆内接正多边形同步练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 357.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 22:53:16 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3-8圆内接正多边形》同步练习题(附答案)
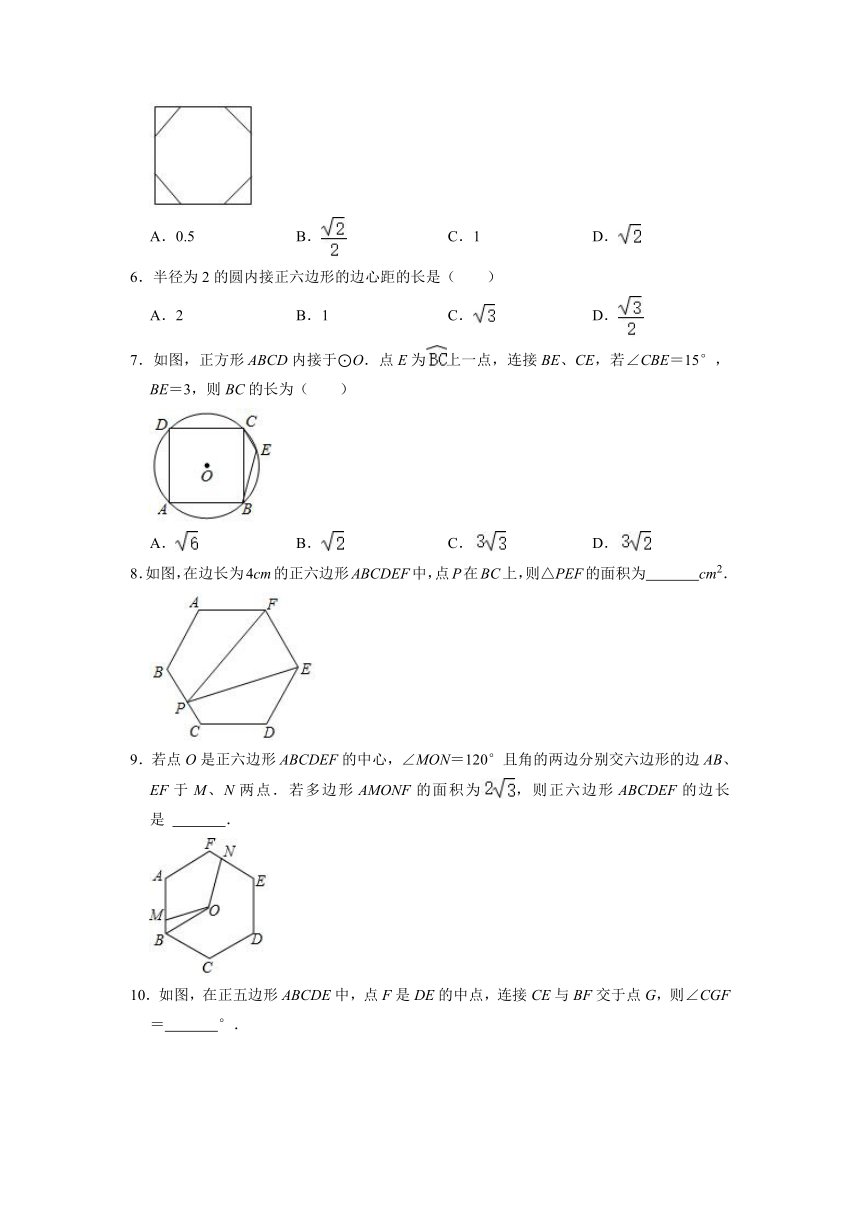
1.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于( )
A.72° B.54° C.36° D.64°
2.如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A.30°或150° B.60°或120° C.30° D.60°
3.如图,正方形ABCD内接于⊙O,AB=4,则图中阴影部分的面积是( )
A.2π﹣4 B.4π﹣4 C.8π﹣4 D.16π﹣4
4.已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C、D外任意一点,则∠CPD的度数为( )
A.30° B.30°或150° C.60° D.60°或120°
5.如图,边长为2+的正方形,剪去四个角后成为一个正八边形,则这个正八边形的边长为( )
A.0.5 B. C.1 D.
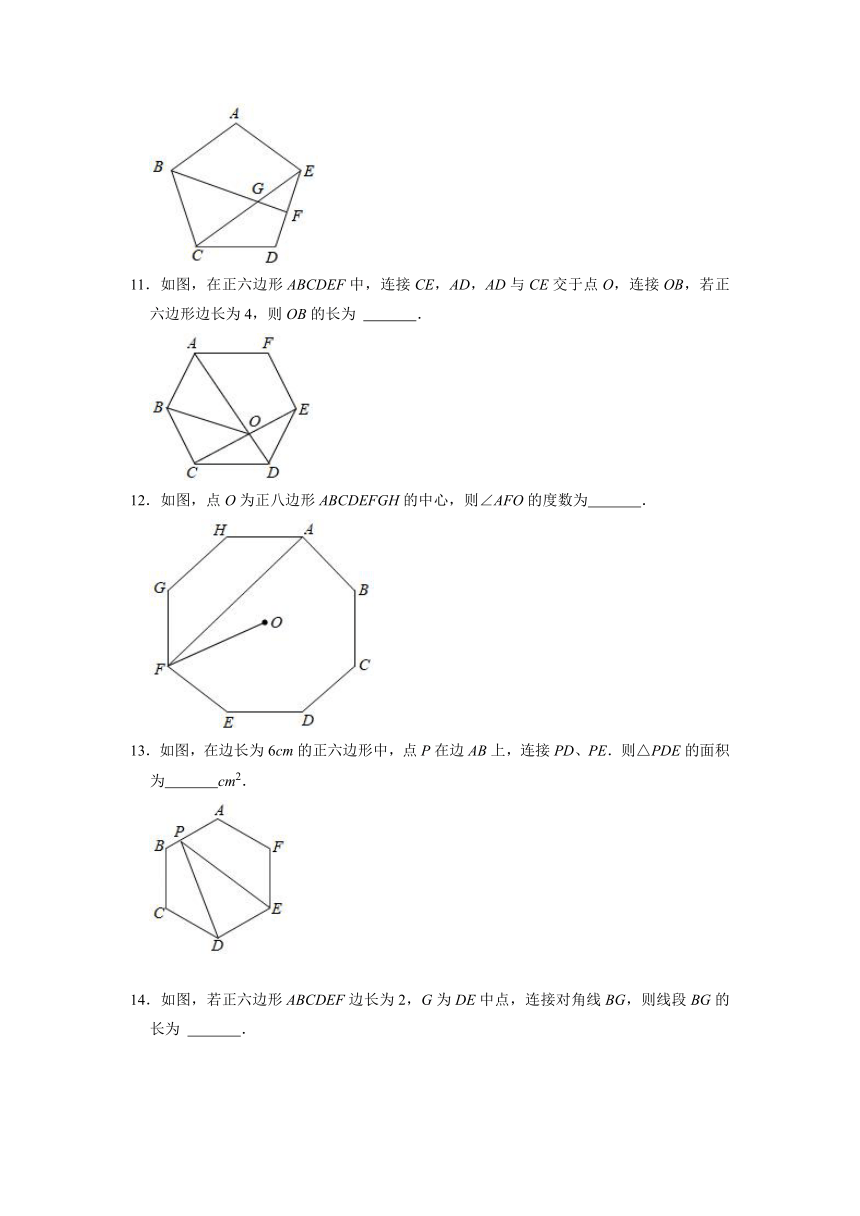
6.半径为2的圆内接正六边形的边心距的长是( )
A.2 B.1 C. D.
7.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
8.如图,在边长为4cm的正六边形ABCDEF中,点P在BC上,则△PEF的面积为 cm2.
9.若点O是正六边形ABCDEF的中心,∠MON=120°且角的两边分别交六边形的边AB、EF于M、N两点.若多边形AMONF的面积为,则正六边形ABCDEF的边长是 .
10.如图,在正五边形ABCDE中,点F是DE的中点,连接CE与BF交于点G,则∠CGF= °.
11.如图,在正六边形ABCDEF中,连接CE,AD,AD与CE交于点O,连接OB,若正六边形边长为4,则OB的长为 .
12.如图,点O为正八边形ABCDEFGH的中心,则∠AFO的度数为 .
13.如图,在边长为6cm的正六边形中,点P在边AB上,连接PD、PE.则△PDE的面积为 cm2.
14.如图,若正六边形ABCDEF边长为2,G为DE中点,连接对角线BG,则线段BG的长为 .
15.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和矩形ABFG,则∠EAG= .
16.如图,正六边形ABCDEF中,AB=1,连接AD,则AD的长为 .
17.中心为O的正六边形ABCDEF的半径为6cm,点P,Q同时分别从A,D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间为t(s).
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.
18.如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
19.如图,在正六边形ABCDEF中,以AD为对角线作正方形APDQ,AP、DP与BC分别交于M、N.
(1)∠BAM= °;
(2)若AB=4,求MN的长.(参考数据:≈1.73,结果精确到0.1,可以直接利用(1)的结论)
20.如图,在正五边形ABCDE中,DF⊥AB.
(1)求∠CDF的度数;
(2)求证:AF=BF.
参考答案
1.解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣36°=54°,
故选:B.
2.解:连接OA,OB,如图所示:
∵六边形ABCDEF是正六边形,
∴∠AOB==60°,
当点P不在上时,
∠APB=∠AOB=30°,
当点P在上时,
∠APB=180°﹣∠AOB=180°﹣30°=150°,
故选:A.
3.解:连接OC、OB,
∵四边形ABCD是正方形,
∴∠COB=90°,∠OCB=45°,
∴OC=CBcos45°=4×=2.
所以阴影部分的面积=(S⊙O﹣S正方形ABCD)÷4=π×(2)2﹣4×4]÷4=2π﹣4.
故选:A.
4.解:连接OC、OD,如图,
∵⊙O是正六边形ABCDEF的外接圆,
∴∠COD=60°,
当P点在弧CAD上时,∠CPD=∠COD=30°,
当P点在弧CD上时,∠CPD=180°﹣30°=150°,
综上所述,∠CPD的度数为30°或150°.
故选:B.
5.解:设正八边形的边长为x,则剪掉的等腰直角三角形的直角边为x,
∵正方形的边长为2+,
∴x+x+x=2+,
解得x==,
∴正八边形的边长为,
故选:D.
6.解:边长为2的正六边形可以分成六个边长为2的正三角形,
而正多边形的边心距即为每个边长为2的正三角形的高,
∴正六多边形的边心距等于2×sin60°=,
故选:C.
7.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
8.解:连接BF,BE,过点A作AT⊥BF于T
∵ABCDEF是正六边形,
∴CB∥EF,AB=AF,∠BAF=120°,
∴S△PEF=S△BEF,
∵AT⊥BF,AB=AF,
∴BT=FT,∠BAT=∠FAT=60°,
∴BT=FT=AB sin60°=2(cm),
∴BF=2BT=4(cm),
∵∠AFE=120°,∠AFB=∠ABF=30°,
∴∠BFE=90°,
∴S△PEF=S△BEF= EF BF=×4×4=8(cm2),
故答案为8.
9.解:连接OF、OA,作OG⊥AF于点G,如图
正六边形中心角∠AOB==60°,
∴∠BOF=60°×2=120°,∠OFE=∠OBA=60°,OF=AF=OA,
∴∠MON﹣∠MOF=∠BOF﹣∠MOF,
即∠FON=∠BOM,
在△FON和△BOM中
,
∴△FON≌△BOM(AAS),
∴S△FON=S△BOM,
∴S多边形AMONF=S四边形ABOF=2S△OAF,
在Rt△OFG中,∠OFG=60°,
sin60°=,
∴OG=OF=AF,
∴S△OAF=AF OG=AF2,
即2×AF2=2,
解得AF=2,
故答案为2.
10.解:连接BE,BD,
∵五边形ABCDE是正五边形,
∴BE=BD,DE=DC,∠CDE=108°,
∴∠DCE=∠DEC=36°,
∵BE=BD,DF=EF,
∴BF⊥DE,
∴∠BFE=90°,
∴∠CGF=∠GFE+∠GEF=90°+36°=126°,
故答案为:126.
11.解:在正六边形ABCDEF中,BC=CD=DE=4,∠BCD=∠CDE=120°,
∴∠DCE=∠DEC=30°,
∵AD⊥CE,
∴OC=OE=CD cos30°=2,
∵∠BCO=∠BCD﹣∠DCO=90°,
∴OB===2,
故答案为:2.
12.解:作正八边形ABCDEFGH的外接圆O.连接OA、OB,
∵八边形ABCDEFGH是OO内接正八边形,
∴∠AOB==45°,
由圆周角定理得,
∠AFO=∠AOB==22.5°,
故选答案为22.5°.
13.解:如图所示,连接OD、OE,
此正六边形中DE=6,
则∠DOE=60°;
∵OD=OE,
∴△ODE是等边三角形,
∵OG⊥DE,
∴∠DOG=30°,
∴OG=OD cos30°=6×=3(cm),
∴△PDE边DE上的高为2OG=6(cm),
∴S△PDE=×6×6=18(cm2),
故答案为18.
14.解:连接BE,过A作AM⊥BE于M,过F作FN⊥BE于N,过G作GH⊥BE于H,
则AF∥BE,
∴四边形AMNF是矩形,
∴MN=AF=2,∠FAM=90°,
∵∠BAF==120°,
∴∠BAM=30°,
∴BM=AB=1,
同理:EN=1,
∴BE=4,EH=,GH=,
∴BH=BE﹣EH=4﹣=,
∴BG===,
方法二:连接BD,
∵正六边形ABCDEF边长为2,G为DE中点,
∴BC=CD=2,DG=DE=1,∠C=∠CDG=120°,
∴∠CDB=30°,
∴∠BDG=90°,
过C作CH⊥BD于H,
∴∠CHD=90°,
∴DH=CD=,
∴BD=2,
∴BG==,
故答案为:.
15.解:∵五边形ABCDE是正五边形,
∴∠EAB=108°,
∵四边形ABFG是矩形,
∴∠BAG=90°,
∴∠EAG=∠EAB﹣∠GAB=108°﹣90°=18°,
故答案为:18°.
16.解:连接AC,
∵在正六边形ABCDEF中,AB=BC=CD,∠B=∠BCD=∠BAF=120°,
∴∠ACB=∠BAC=30°,
∴∠ACD=90°,
∵∠BAD=∠FAD=60°,
∴∠CAD=30°,
∴AD=2CD=2AB=2,
故答案为:2.
17.(1)证明:∵六边形ABCDEF是正六边形,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,
∴AP=DQ=t,PF=QC=6﹣t,
在△ABP和△DEQ中,
,
∴△ABP≌△DEQ(SAS),
∴BP=EQ,
同理可证PE=QB,
∴四边形PEQB为平行四边形.
(2)解:连接BE、OA,则∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=6,BE=2OB=12,
当t=0时,点P与A重合,Q与D重合,四边形PBQE即为四边形ABDE,如图1所示:
则∠EAF=∠AEF=30°,
∴∠BAE=∠BAF﹣∠FAE=120°﹣30°=90°,
∴此时四边形ABDE是矩形,即四边形PBQE是矩形.
当t=6时,点P与F重合,Q与C重合,四边形PBQE即为四边形FBCE,如图2所示:
同法可知∠BFE=90°,此时四边形PBQE是矩形.
综上所述,t=0s或6s时,四边形PBQE是矩形,
∴AE==6,
∴矩形PBQE的面积=矩形ABDE的面积=AB×AE=6×6=36;
∵正六边形ABCDEF的面积=6△AOB的面积=6×矩形ABDE的面积=6××36=54,
∴矩形PBQE的面积与正六边形ABCDEF的面积之比=.
18.解:(1)连接OD,OC,
∵正方形ABCD内接于⊙O,
∴∠DOC=90°.
∴;
(2)连接PO,OB,
∵正方形ABCD内接于⊙O,
∴∠COB=90°,
∵点P为BC的中点,
∴=,
∴,
∴n=360÷45=8.
19.解:(1)在正六边形ABCDEF中,∠DAB=60°,
在正方形AQDP中,∠DAP=45°,
∴∠BAM=∠DAB﹣∠DAP=60°﹣45°=15°,
故答案为:15.
(2)连接BE交AD于点O,连接OP交BC于H.
在正六边形ABCDEF 中,CD=BC=AB=4,∠BAF=∠ABC=∠C=∠CDE=120°,
AO、BO 平分∠BAF、∠ABC,OA=OB,
∴∠BAO=∠ABO=∠CBO=×120°=60°,
∴△ABO 是等边三角形,
∴BC∥AD,AO=BO=AB=4,
∴AD=2AO=8,
在正方形APDQ 中,AP=DP,∠APD=90°,
∵AO=DO,
∴PO=AD=4,PO⊥AD,∠APO=∠DPO=∠APD=45°,
∵AD∥BC,
∴∠MHP=∠AOP=90°,
∴∠BHO=90°,
∴sin∠OBH=,
∵∠OBH=60°,BO=4,
∴OH=4×sin60°=2,
∵PH=MH=OP﹣OH=4﹣2,
∴MN=2MH=8﹣4≈1.1.
20.(1)解:在正五边形中,∠ABC=∠C=540°÷5=108°,
∵DF⊥AB,
∴∠DFB=90°,
在四边形BCDF中,
∵∠ABC+∠C+∠DFB+∠CDF=360°,
∴∠CDF=360°﹣∠ABC﹣∠C﹣∠DFB=360°﹣108°﹣108°﹣90°=54°;
(2)证明:如图,连接DB、AD,
∵ABCDE是正五边形,
∴∠E=∠C,DE=AE=DC=BC,
在△AED和△BCD中,
,
∴△AED≌△BCD(SAS),
∴AD=BD,
∵DF⊥AB,
∴∠DFA=∠DFB=90°,
Rt△DAF和Rt△DFB,
,
∴Rt△DAF≌Rt△DFB(HL),
∴AF=BF.
1.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于( )
A.72° B.54° C.36° D.64°
2.如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A.30°或150° B.60°或120° C.30° D.60°
3.如图,正方形ABCD内接于⊙O,AB=4,则图中阴影部分的面积是( )
A.2π﹣4 B.4π﹣4 C.8π﹣4 D.16π﹣4
4.已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C、D外任意一点,则∠CPD的度数为( )
A.30° B.30°或150° C.60° D.60°或120°
5.如图,边长为2+的正方形,剪去四个角后成为一个正八边形,则这个正八边形的边长为( )
A.0.5 B. C.1 D.
6.半径为2的圆内接正六边形的边心距的长是( )
A.2 B.1 C. D.
7.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
8.如图,在边长为4cm的正六边形ABCDEF中,点P在BC上,则△PEF的面积为 cm2.
9.若点O是正六边形ABCDEF的中心,∠MON=120°且角的两边分别交六边形的边AB、EF于M、N两点.若多边形AMONF的面积为,则正六边形ABCDEF的边长是 .
10.如图,在正五边形ABCDE中,点F是DE的中点,连接CE与BF交于点G,则∠CGF= °.
11.如图,在正六边形ABCDEF中,连接CE,AD,AD与CE交于点O,连接OB,若正六边形边长为4,则OB的长为 .
12.如图,点O为正八边形ABCDEFGH的中心,则∠AFO的度数为 .
13.如图,在边长为6cm的正六边形中,点P在边AB上,连接PD、PE.则△PDE的面积为 cm2.
14.如图,若正六边形ABCDEF边长为2,G为DE中点,连接对角线BG,则线段BG的长为 .
15.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和矩形ABFG,则∠EAG= .
16.如图,正六边形ABCDEF中,AB=1,连接AD,则AD的长为 .
17.中心为O的正六边形ABCDEF的半径为6cm,点P,Q同时分别从A,D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间为t(s).
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.
18.如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
19.如图,在正六边形ABCDEF中,以AD为对角线作正方形APDQ,AP、DP与BC分别交于M、N.
(1)∠BAM= °;
(2)若AB=4,求MN的长.(参考数据:≈1.73,结果精确到0.1,可以直接利用(1)的结论)
20.如图,在正五边形ABCDE中,DF⊥AB.
(1)求∠CDF的度数;
(2)求证:AF=BF.
参考答案
1.解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣36°=54°,
故选:B.
2.解:连接OA,OB,如图所示:
∵六边形ABCDEF是正六边形,
∴∠AOB==60°,
当点P不在上时,
∠APB=∠AOB=30°,
当点P在上时,
∠APB=180°﹣∠AOB=180°﹣30°=150°,
故选:A.
3.解:连接OC、OB,
∵四边形ABCD是正方形,
∴∠COB=90°,∠OCB=45°,
∴OC=CBcos45°=4×=2.
所以阴影部分的面积=(S⊙O﹣S正方形ABCD)÷4=π×(2)2﹣4×4]÷4=2π﹣4.
故选:A.
4.解:连接OC、OD,如图,
∵⊙O是正六边形ABCDEF的外接圆,
∴∠COD=60°,
当P点在弧CAD上时,∠CPD=∠COD=30°,
当P点在弧CD上时,∠CPD=180°﹣30°=150°,
综上所述,∠CPD的度数为30°或150°.
故选:B.
5.解:设正八边形的边长为x,则剪掉的等腰直角三角形的直角边为x,
∵正方形的边长为2+,
∴x+x+x=2+,
解得x==,
∴正八边形的边长为,
故选:D.
6.解:边长为2的正六边形可以分成六个边长为2的正三角形,
而正多边形的边心距即为每个边长为2的正三角形的高,
∴正六多边形的边心距等于2×sin60°=,
故选:C.
7.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
8.解:连接BF,BE,过点A作AT⊥BF于T
∵ABCDEF是正六边形,
∴CB∥EF,AB=AF,∠BAF=120°,
∴S△PEF=S△BEF,
∵AT⊥BF,AB=AF,
∴BT=FT,∠BAT=∠FAT=60°,
∴BT=FT=AB sin60°=2(cm),
∴BF=2BT=4(cm),
∵∠AFE=120°,∠AFB=∠ABF=30°,
∴∠BFE=90°,
∴S△PEF=S△BEF= EF BF=×4×4=8(cm2),
故答案为8.
9.解:连接OF、OA,作OG⊥AF于点G,如图
正六边形中心角∠AOB==60°,
∴∠BOF=60°×2=120°,∠OFE=∠OBA=60°,OF=AF=OA,
∴∠MON﹣∠MOF=∠BOF﹣∠MOF,
即∠FON=∠BOM,
在△FON和△BOM中
,
∴△FON≌△BOM(AAS),
∴S△FON=S△BOM,
∴S多边形AMONF=S四边形ABOF=2S△OAF,
在Rt△OFG中,∠OFG=60°,
sin60°=,
∴OG=OF=AF,
∴S△OAF=AF OG=AF2,
即2×AF2=2,
解得AF=2,
故答案为2.
10.解:连接BE,BD,
∵五边形ABCDE是正五边形,
∴BE=BD,DE=DC,∠CDE=108°,
∴∠DCE=∠DEC=36°,
∵BE=BD,DF=EF,
∴BF⊥DE,
∴∠BFE=90°,
∴∠CGF=∠GFE+∠GEF=90°+36°=126°,
故答案为:126.
11.解:在正六边形ABCDEF中,BC=CD=DE=4,∠BCD=∠CDE=120°,
∴∠DCE=∠DEC=30°,
∵AD⊥CE,
∴OC=OE=CD cos30°=2,
∵∠BCO=∠BCD﹣∠DCO=90°,
∴OB===2,
故答案为:2.
12.解:作正八边形ABCDEFGH的外接圆O.连接OA、OB,
∵八边形ABCDEFGH是OO内接正八边形,
∴∠AOB==45°,
由圆周角定理得,
∠AFO=∠AOB==22.5°,
故选答案为22.5°.
13.解:如图所示,连接OD、OE,
此正六边形中DE=6,
则∠DOE=60°;
∵OD=OE,
∴△ODE是等边三角形,
∵OG⊥DE,
∴∠DOG=30°,
∴OG=OD cos30°=6×=3(cm),
∴△PDE边DE上的高为2OG=6(cm),
∴S△PDE=×6×6=18(cm2),
故答案为18.
14.解:连接BE,过A作AM⊥BE于M,过F作FN⊥BE于N,过G作GH⊥BE于H,
则AF∥BE,
∴四边形AMNF是矩形,
∴MN=AF=2,∠FAM=90°,
∵∠BAF==120°,
∴∠BAM=30°,
∴BM=AB=1,
同理:EN=1,
∴BE=4,EH=,GH=,
∴BH=BE﹣EH=4﹣=,
∴BG===,
方法二:连接BD,
∵正六边形ABCDEF边长为2,G为DE中点,
∴BC=CD=2,DG=DE=1,∠C=∠CDG=120°,
∴∠CDB=30°,
∴∠BDG=90°,
过C作CH⊥BD于H,
∴∠CHD=90°,
∴DH=CD=,
∴BD=2,
∴BG==,
故答案为:.
15.解:∵五边形ABCDE是正五边形,
∴∠EAB=108°,
∵四边形ABFG是矩形,
∴∠BAG=90°,
∴∠EAG=∠EAB﹣∠GAB=108°﹣90°=18°,
故答案为:18°.
16.解:连接AC,
∵在正六边形ABCDEF中,AB=BC=CD,∠B=∠BCD=∠BAF=120°,
∴∠ACB=∠BAC=30°,
∴∠ACD=90°,
∵∠BAD=∠FAD=60°,
∴∠CAD=30°,
∴AD=2CD=2AB=2,
故答案为:2.
17.(1)证明:∵六边形ABCDEF是正六边形,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,
∴AP=DQ=t,PF=QC=6﹣t,
在△ABP和△DEQ中,
,
∴△ABP≌△DEQ(SAS),
∴BP=EQ,
同理可证PE=QB,
∴四边形PEQB为平行四边形.
(2)解:连接BE、OA,则∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=6,BE=2OB=12,
当t=0时,点P与A重合,Q与D重合,四边形PBQE即为四边形ABDE,如图1所示:
则∠EAF=∠AEF=30°,
∴∠BAE=∠BAF﹣∠FAE=120°﹣30°=90°,
∴此时四边形ABDE是矩形,即四边形PBQE是矩形.
当t=6时,点P与F重合,Q与C重合,四边形PBQE即为四边形FBCE,如图2所示:
同法可知∠BFE=90°,此时四边形PBQE是矩形.
综上所述,t=0s或6s时,四边形PBQE是矩形,
∴AE==6,
∴矩形PBQE的面积=矩形ABDE的面积=AB×AE=6×6=36;
∵正六边形ABCDEF的面积=6△AOB的面积=6×矩形ABDE的面积=6××36=54,
∴矩形PBQE的面积与正六边形ABCDEF的面积之比=.
18.解:(1)连接OD,OC,
∵正方形ABCD内接于⊙O,
∴∠DOC=90°.
∴;
(2)连接PO,OB,
∵正方形ABCD内接于⊙O,
∴∠COB=90°,
∵点P为BC的中点,
∴=,
∴,
∴n=360÷45=8.
19.解:(1)在正六边形ABCDEF中,∠DAB=60°,
在正方形AQDP中,∠DAP=45°,
∴∠BAM=∠DAB﹣∠DAP=60°﹣45°=15°,
故答案为:15.
(2)连接BE交AD于点O,连接OP交BC于H.
在正六边形ABCDEF 中,CD=BC=AB=4,∠BAF=∠ABC=∠C=∠CDE=120°,
AO、BO 平分∠BAF、∠ABC,OA=OB,
∴∠BAO=∠ABO=∠CBO=×120°=60°,
∴△ABO 是等边三角形,
∴BC∥AD,AO=BO=AB=4,
∴AD=2AO=8,
在正方形APDQ 中,AP=DP,∠APD=90°,
∵AO=DO,
∴PO=AD=4,PO⊥AD,∠APO=∠DPO=∠APD=45°,
∵AD∥BC,
∴∠MHP=∠AOP=90°,
∴∠BHO=90°,
∴sin∠OBH=,
∵∠OBH=60°,BO=4,
∴OH=4×sin60°=2,
∵PH=MH=OP﹣OH=4﹣2,
∴MN=2MH=8﹣4≈1.1.
20.(1)解:在正五边形中,∠ABC=∠C=540°÷5=108°,
∵DF⊥AB,
∴∠DFB=90°,
在四边形BCDF中,
∵∠ABC+∠C+∠DFB+∠CDF=360°,
∴∠CDF=360°﹣∠ABC﹣∠C﹣∠DFB=360°﹣108°﹣108°﹣90°=54°;
(2)证明:如图,连接DB、AD,
∵ABCDE是正五边形,
∴∠E=∠C,DE=AE=DC=BC,
在△AED和△BCD中,
,
∴△AED≌△BCD(SAS),
∴AD=BD,
∵DF⊥AB,
∴∠DFA=∠DFB=90°,
Rt△DAF和Rt△DFB,
,
∴Rt△DAF≌Rt△DFB(HL),
∴AF=BF.
