人教版数学 七年级下册 5.1.2 垂线 课件(共39张PPT)
文档属性
| 名称 | 人教版数学 七年级下册 5.1.2 垂线 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览







文档简介
(共39张PPT)
5.1.2垂线
1.能说出垂线的意义、会用三角尺或量角器过一点画已知直线的垂线.
2.记住垂线的性质并会利用所学知识进行简单的推理. (重点、难点)
学习目标
取两根木条a、b,将它们钉在一起,固定木条a,转动木条b.
1)当a与b所成锐角α为35°时,其余的角分别为多少?
2)当a与b所成锐角α为70°时,其余的角分别为多少?
按照顺时针方式,其余角分别为:145°、35°、145°
知识回顾
按照顺时针方式,其余角分别为:130°、70°、130°
观察结果,你发现了什么?
a与b所成角随木条b的转动而变化
问题2:相交直线形成的四个角中,
按照两个角的位置关系分
类,有哪两种类型的角?
1
2
3
4
A
B
C
D
O
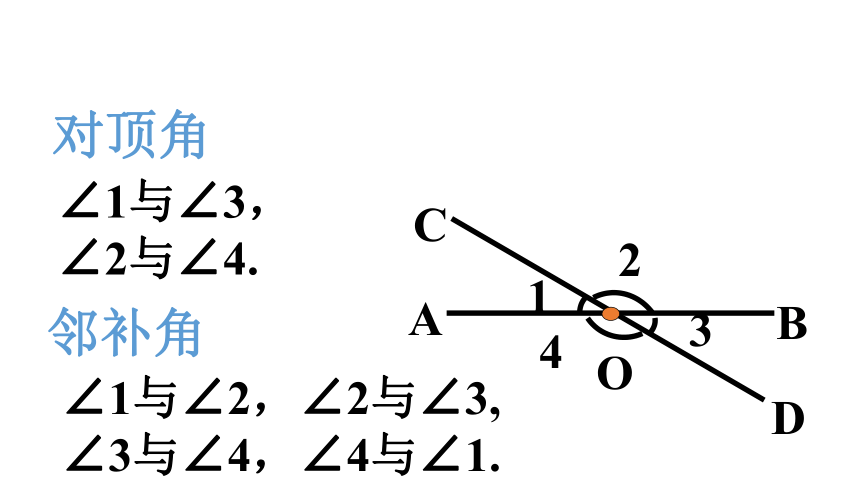
对顶角
邻补角
∠1与∠3,
∠2与∠4.
∠1与∠2,∠2与∠3,
∠3与∠4,∠4与∠1.
A
B
C
D
A
B
C
D
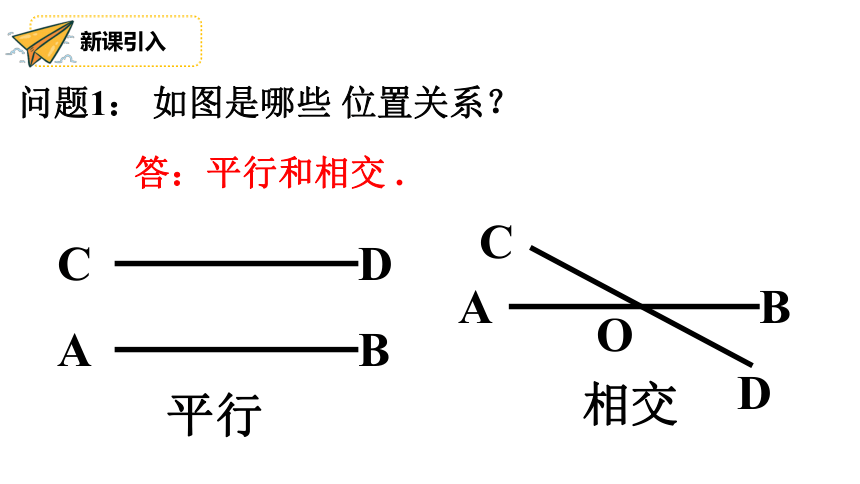
平行
相交
O
问题1:平面上的两条直线有
问题1: 如图是哪些 位置关系?
答:平行和相交 .
新课引入
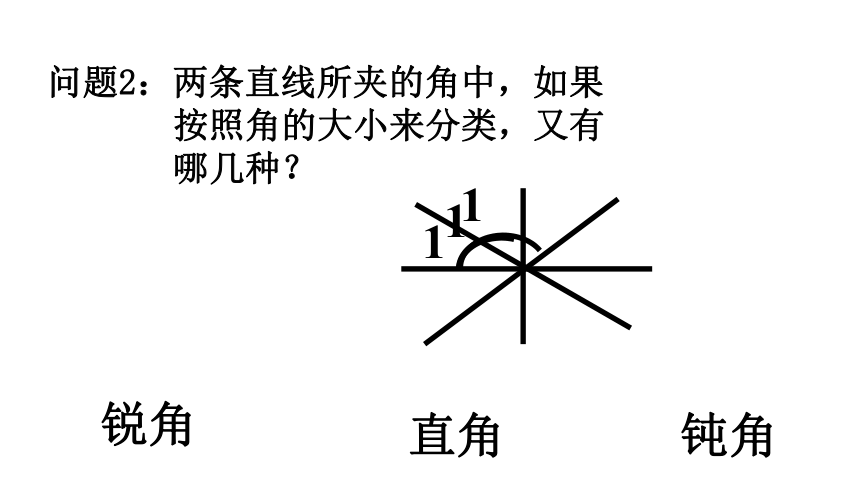
问题2:两条直线所夹的角中,如果
按照角的大小来分类,又有
哪几种?
1
锐角
直角
钝角
1
1
过一点有且只有一条直线与已知直线垂直.
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
垂线的性质(1):
新课讲解
如图所示, 村庄A要从河流 l 引水入庄, 需修筑一
水渠, 如何修水渠最短呢?
同学们,请回忆一下曾经学过什么最短的知识?
两点之间,线段最短。
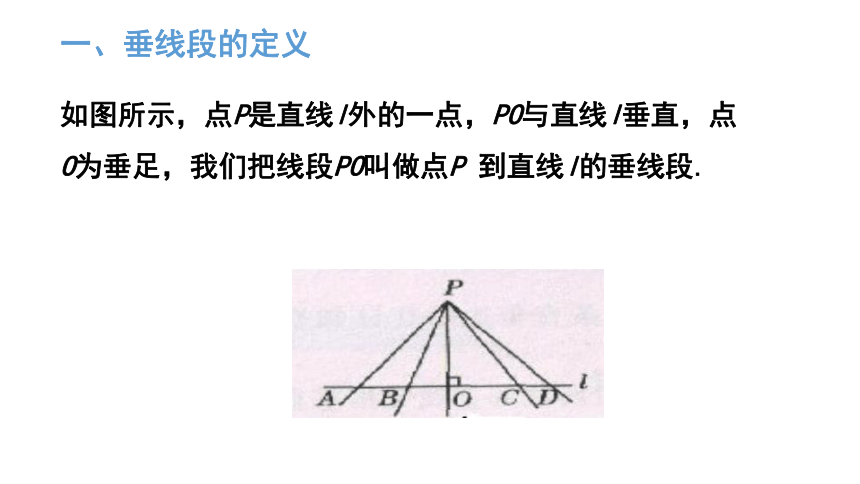
一、垂线段的定义
如图所示,点P是直线l外的一点,PO与直线l垂直,点O为垂足,我们把线段PO叫做点P 到直线l的垂线段.
小 结
过直线外一点画已知直线的垂线,连接这点与垂足之间的线段,叫做这点到已知直线的垂线段.
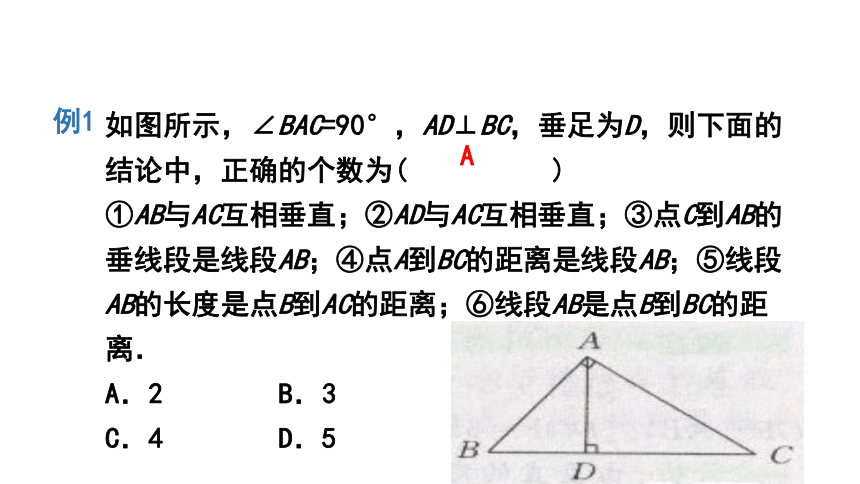
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AB;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到BC的距离.
A.2 B.3
C.4 D.5
例1
A
根据垂直定义,可知①正确,②错误;点C 到AB
的垂线段应是线段AC,故③错误;点到直线的距
离是线段的长度而不是线段,故④⑥错误;⑤符
合定义,正确.
分析:
小 结
解答概念、性质辨析题,首先要熟记概念和性质,然后根据垂线的定义与性质、垂线段与点到直线距离的概念作出正确的判断即可.所以记忆与理解相结合是学好数学的前提.
二:垂线段的性质
连接直线外一点与直线上各点的所有线段中,垂线段最短。
P
A
B
C
m
D
简单说成:垂线段最短.
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.
A
B
P
D
特别强调:
如图所示,AB是一条河流,要铺设管道将河水引
到C、D两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D作AB的垂线,垂足分别为点E,F,沿CE,DF铺设管道;
方案二:连接CD交AB于点P,
沿PC,PD铺设管道.
这两种铺设管道的方案哪一种
更节省材料?为什么?
(忽略河流的宽度)
例2
要尽可能节省材料,也就是让管道的总长度最
短.方案一中CE,DF是垂线段,而方案二中PC,
PD不是垂线段,所以CE<PC,DF<PD,所以
CE+DF<PC+PD,所以方案一更节省材料.
解:
导引:
按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,CD不垂直于AB,
根据“垂线段最短”可知,CE<PC,DF<DP,
所以CE+DF<PC+DP.
所以沿CE,DF铺设管道更节省材料.
小 结
本题主要利用“垂线段最短”来解决实际问题,解这类求最短距离问题时,要注意“垂线段最短”与“两点之间,线段最短”的区别,辨明这两条性质的应用条件:点到直线的距离,两点间的距离;正确运用解题方法.
三:点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
l
A
例如:如图,PA⊥l于点A ,垂线段PA的长度叫做点P到直线l的距离.
例:如图,是一个同学跳远的位置跳远成绩怎么表示
l
P
A
解:过P点作PA⊥l于点A ,垂线段PA的长度就是该同学的跳远成绩.
例3 如图,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为______cm,点B到直线AC的距离为______cm,点C 到直线AB的距离为______cm.
4
3
2.4
导引:根据点到直线的距离的定义可知,点A到直线BC
的距离是线段AC的长,点B到直线AC的距离是线段BC的长,点C到直线AB的距离是线段CD的长.
因为三角形ABC的面积S=
所以AC·BC=AB·CD,进而可得CD=2.4 cm.
小 结
正确理解点到直线的距离及两点间的距离是解决此类问题的关键.解决此类问题应注意:
(1)点到直线的距离是点到直线的垂线段的长度,而不是垂线,也不是垂线段;
(2)距离表示线段的长度,是一个数量,与线段不能等同;
(3)用垂线段的长度表示点到直线的距离,其实质是点与垂足两点间的距离,体现了数形结合思想.
思考
(1)用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
(2)经过一点画已知直线l的垂线,这样的垂线能画出几条?
性质1
垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直。
P
l
l
P
练一练
过点P画出射线AB或线段AB 的垂线。
性质2
(1)在直线上有无数个点,试着取几个点与点P相连,比较一下它们的大小关系.你有什么发现?
(2)你能猜想一下最短的位置会在哪儿?它唯一吗?为什么?
(3)你能用一句话总结出观察得出的结论吗?
垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短.
性质
点到直线的距离:
直线外一点到这条直线的垂线段的长度,叫点到直线的距离.
1、在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
C
小试牛刀
2、如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为_________°.
45
3、如图,已知直线CD,EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=______________.
30°
1、如图,OA⊥OB,∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.70°
C
课堂练习
2、 过点 P 向线段 AB 所在直线引垂线,正确的是( ).
A B C D
C
3、若直线m、n相交于点O,∠1=90°,则直线m、n的位置关系是 ______。(用符号表示)
O
m
n
1
m⊥n
O
C
B
D
A
90°
4、若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD=___。
5、如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
6、如图所示,AB⊥AC,AD⊥BC,垂足分别为点A,D,AB=6 cm,AD=5 cm,则点B到直线AC的距离是________,点A到直线BC的距离是__________.
6 cm
5 cm
归纳总结
判断两直线(线段、射线所在直线)互相垂直,主要依据是垂直定义,只要说明两条相交直线所构成的四个角中有一个角是直角即可.
课堂总结
知识小结
以下几个方面由学生自己总结:
① 垂线的定义及垂直的符号表示;
② 垂线的有关性质;
③过一点作已知直线的垂线的方法.
课堂总结
5.1.2垂线
1.能说出垂线的意义、会用三角尺或量角器过一点画已知直线的垂线.
2.记住垂线的性质并会利用所学知识进行简单的推理. (重点、难点)
学习目标
取两根木条a、b,将它们钉在一起,固定木条a,转动木条b.
1)当a与b所成锐角α为35°时,其余的角分别为多少?
2)当a与b所成锐角α为70°时,其余的角分别为多少?
按照顺时针方式,其余角分别为:145°、35°、145°
知识回顾
按照顺时针方式,其余角分别为:130°、70°、130°
观察结果,你发现了什么?
a与b所成角随木条b的转动而变化
问题2:相交直线形成的四个角中,
按照两个角的位置关系分
类,有哪两种类型的角?
1
2
3
4
A
B
C
D
O
对顶角
邻补角
∠1与∠3,
∠2与∠4.
∠1与∠2,∠2与∠3,
∠3与∠4,∠4与∠1.
A
B
C
D
A
B
C
D
平行
相交
O
问题1:平面上的两条直线有
问题1: 如图是哪些 位置关系?
答:平行和相交 .
新课引入
问题2:两条直线所夹的角中,如果
按照角的大小来分类,又有
哪几种?
1
锐角
直角
钝角
1
1
过一点有且只有一条直线与已知直线垂直.
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
垂线的性质(1):
新课讲解
如图所示, 村庄A要从河流 l 引水入庄, 需修筑一
水渠, 如何修水渠最短呢?
同学们,请回忆一下曾经学过什么最短的知识?
两点之间,线段最短。
一、垂线段的定义
如图所示,点P是直线l外的一点,PO与直线l垂直,点O为垂足,我们把线段PO叫做点P 到直线l的垂线段.
小 结
过直线外一点画已知直线的垂线,连接这点与垂足之间的线段,叫做这点到已知直线的垂线段.
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AB;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到BC的距离.
A.2 B.3
C.4 D.5
例1
A
根据垂直定义,可知①正确,②错误;点C 到AB
的垂线段应是线段AC,故③错误;点到直线的距
离是线段的长度而不是线段,故④⑥错误;⑤符
合定义,正确.
分析:
小 结
解答概念、性质辨析题,首先要熟记概念和性质,然后根据垂线的定义与性质、垂线段与点到直线距离的概念作出正确的判断即可.所以记忆与理解相结合是学好数学的前提.
二:垂线段的性质
连接直线外一点与直线上各点的所有线段中,垂线段最短。
P
A
B
C
m
D
简单说成:垂线段最短.
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.
A
B
P
D
特别强调:
如图所示,AB是一条河流,要铺设管道将河水引
到C、D两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D作AB的垂线,垂足分别为点E,F,沿CE,DF铺设管道;
方案二:连接CD交AB于点P,
沿PC,PD铺设管道.
这两种铺设管道的方案哪一种
更节省材料?为什么?
(忽略河流的宽度)
例2
要尽可能节省材料,也就是让管道的总长度最
短.方案一中CE,DF是垂线段,而方案二中PC,
PD不是垂线段,所以CE<PC,DF<PD,所以
CE+DF<PC+PD,所以方案一更节省材料.
解:
导引:
按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,CD不垂直于AB,
根据“垂线段最短”可知,CE<PC,DF<DP,
所以CE+DF<PC+DP.
所以沿CE,DF铺设管道更节省材料.
小 结
本题主要利用“垂线段最短”来解决实际问题,解这类求最短距离问题时,要注意“垂线段最短”与“两点之间,线段最短”的区别,辨明这两条性质的应用条件:点到直线的距离,两点间的距离;正确运用解题方法.
三:点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
l
A
例如:如图,PA⊥l于点A ,垂线段PA的长度叫做点P到直线l的距离.
例:如图,是一个同学跳远的位置跳远成绩怎么表示
l
P
A
解:过P点作PA⊥l于点A ,垂线段PA的长度就是该同学的跳远成绩.
例3 如图,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为______cm,点B到直线AC的距离为______cm,点C 到直线AB的距离为______cm.
4
3
2.4
导引:根据点到直线的距离的定义可知,点A到直线BC
的距离是线段AC的长,点B到直线AC的距离是线段BC的长,点C到直线AB的距离是线段CD的长.
因为三角形ABC的面积S=
所以AC·BC=AB·CD,进而可得CD=2.4 cm.
小 结
正确理解点到直线的距离及两点间的距离是解决此类问题的关键.解决此类问题应注意:
(1)点到直线的距离是点到直线的垂线段的长度,而不是垂线,也不是垂线段;
(2)距离表示线段的长度,是一个数量,与线段不能等同;
(3)用垂线段的长度表示点到直线的距离,其实质是点与垂足两点间的距离,体现了数形结合思想.
思考
(1)用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
(2)经过一点画已知直线l的垂线,这样的垂线能画出几条?
性质1
垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直。
P
l
l
P
练一练
过点P画出射线AB或线段AB 的垂线。
性质2
(1)在直线上有无数个点,试着取几个点与点P相连,比较一下它们的大小关系.你有什么发现?
(2)你能猜想一下最短的位置会在哪儿?它唯一吗?为什么?
(3)你能用一句话总结出观察得出的结论吗?
垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短.
性质
点到直线的距离:
直线外一点到这条直线的垂线段的长度,叫点到直线的距离.
1、在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
C
小试牛刀
2、如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为_________°.
45
3、如图,已知直线CD,EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=______________.
30°
1、如图,OA⊥OB,∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.70°
C
课堂练习
2、 过点 P 向线段 AB 所在直线引垂线,正确的是( ).
A B C D
C
3、若直线m、n相交于点O,∠1=90°,则直线m、n的位置关系是 ______。(用符号表示)
O
m
n
1
m⊥n
O
C
B
D
A
90°
4、若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD=___。
5、如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
6、如图所示,AB⊥AC,AD⊥BC,垂足分别为点A,D,AB=6 cm,AD=5 cm,则点B到直线AC的距离是________,点A到直线BC的距离是__________.
6 cm
5 cm
归纳总结
判断两直线(线段、射线所在直线)互相垂直,主要依据是垂直定义,只要说明两条相交直线所构成的四个角中有一个角是直角即可.
课堂总结
知识小结
以下几个方面由学生自己总结:
① 垂线的定义及垂直的符号表示;
② 垂线的有关性质;
③过一点作已知直线的垂线的方法.
课堂总结
