函数y=Asin(ωx+ψ)的图像
图片预览






文档简介
课件40张PPT。函 数
y=Asin(?x+?)的图象学习目标:
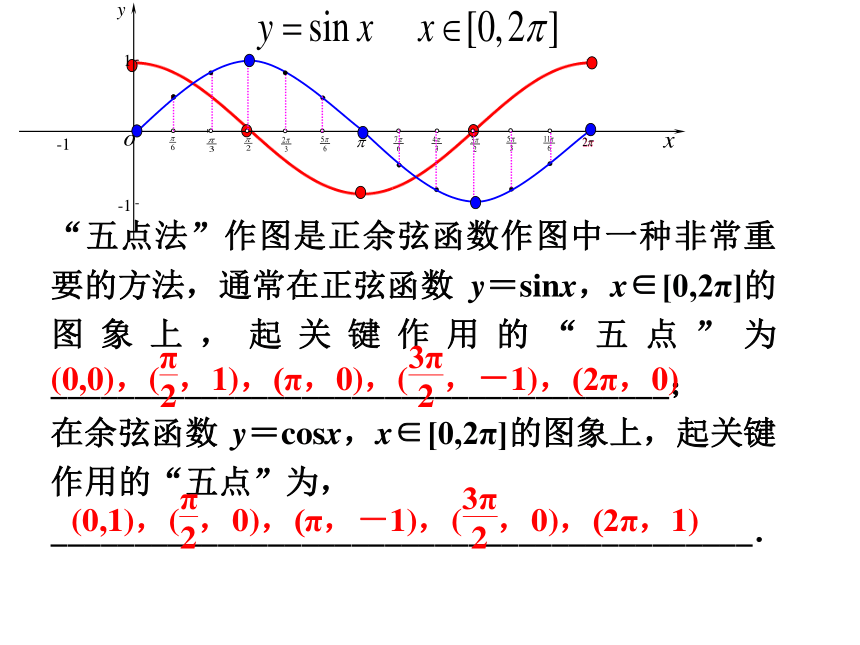
1、用五点法画函数的图象.
2、能由正弦曲线通过平移、伸缩变换得到的图象,并在这个过程中认识到函数与得联系
重点难点:
1、用五点法列表画函数图象;
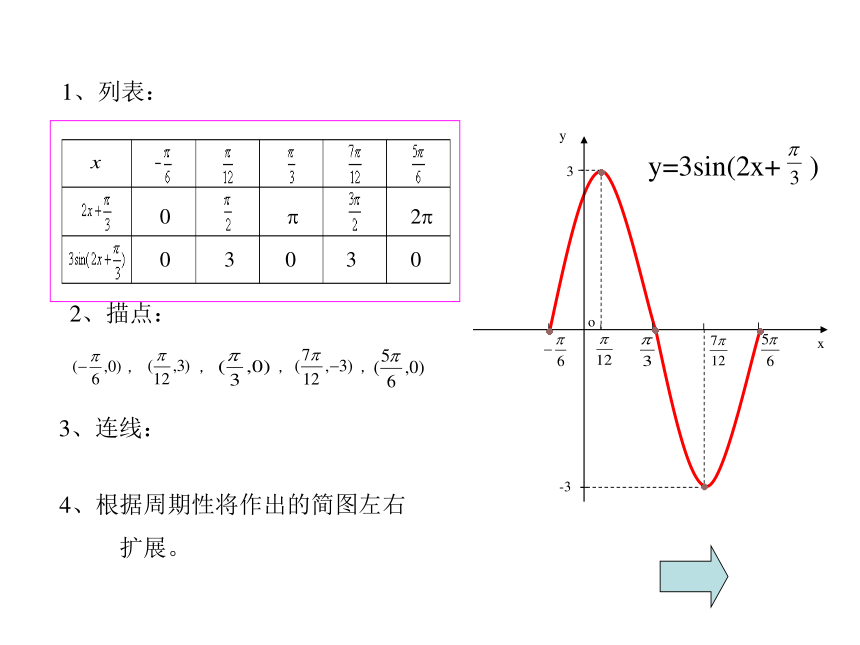
2、理解的图象与的图象之间的变换关系.函数y=Asin(ωx+ ?),其中(A>0, ω >0)的图像与函数y=sinx的图象有什么关系呢?例、 作函数 y = 3sin(2 + )的简图五点作图法3、连线:4、根据周期性将作出的简图左右
扩展。能不能通过变换y=sinx的图象作出函数y=Asin(ωx+ ?) 的图象?
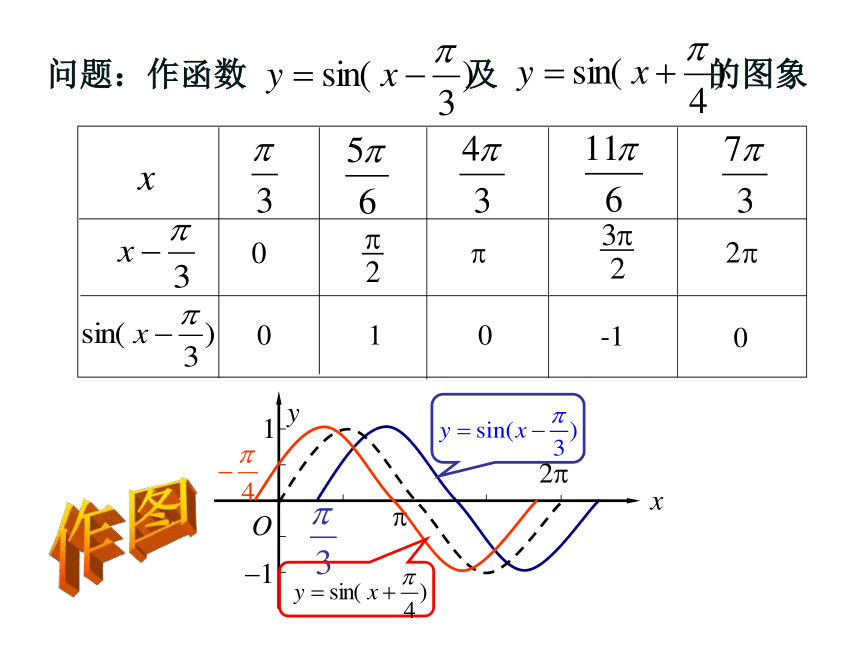
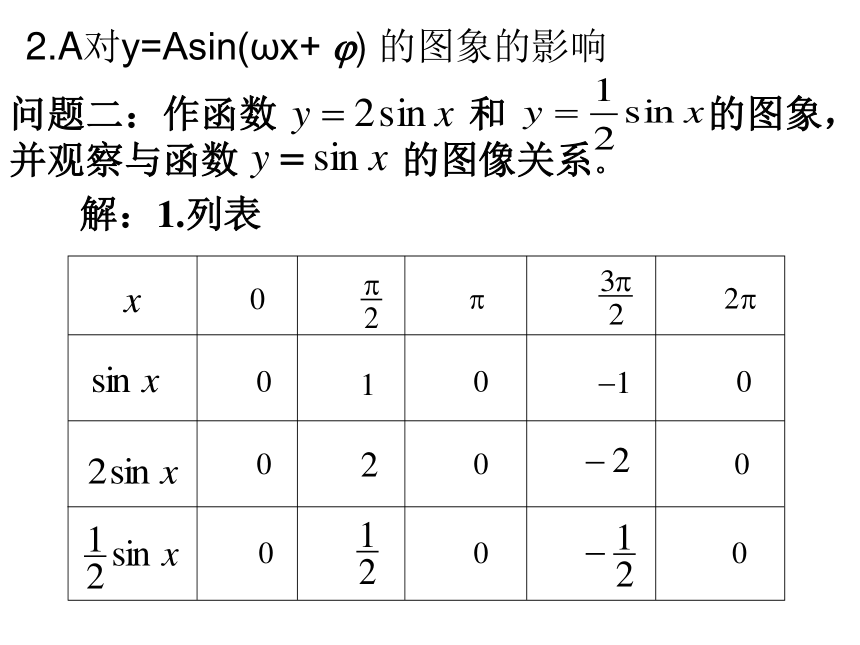
问题一:画函数 和 的图
象,并观察与 的图象关系.
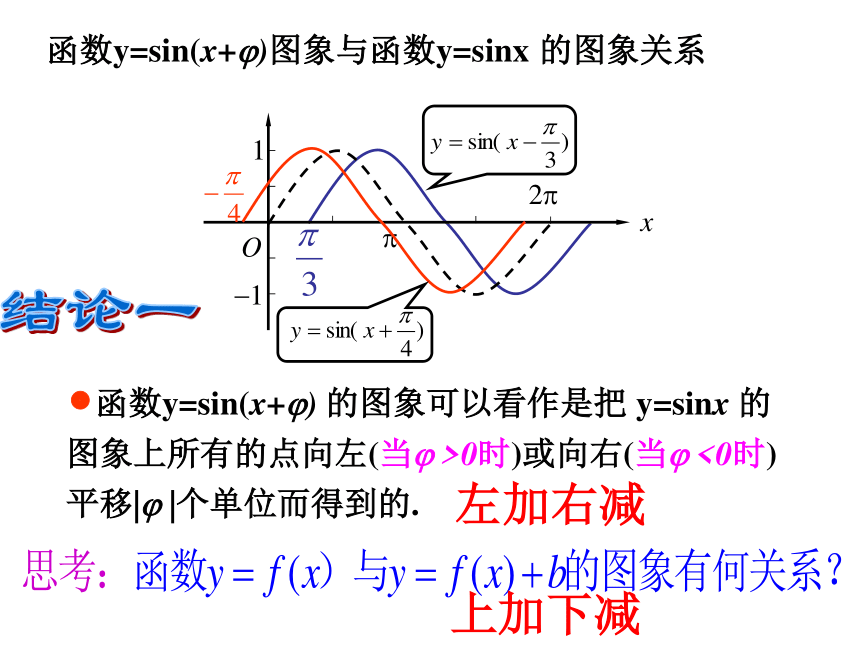
1. ?对y=Asin(ωx+ ?) 的图象的影响问题:作函数 及 的图象 作图函数y=sin(x+?)图象与函数y=sinx 的图象关系 ?函数y=sin(x+?) 的图象可以看作是把 y=sinx 的图象上所有的点向左(当? >0时)或向右(当? <0时)平移|? |个单位而得到的.结论一x解:1.列表问题二:作函数 和 的图象,
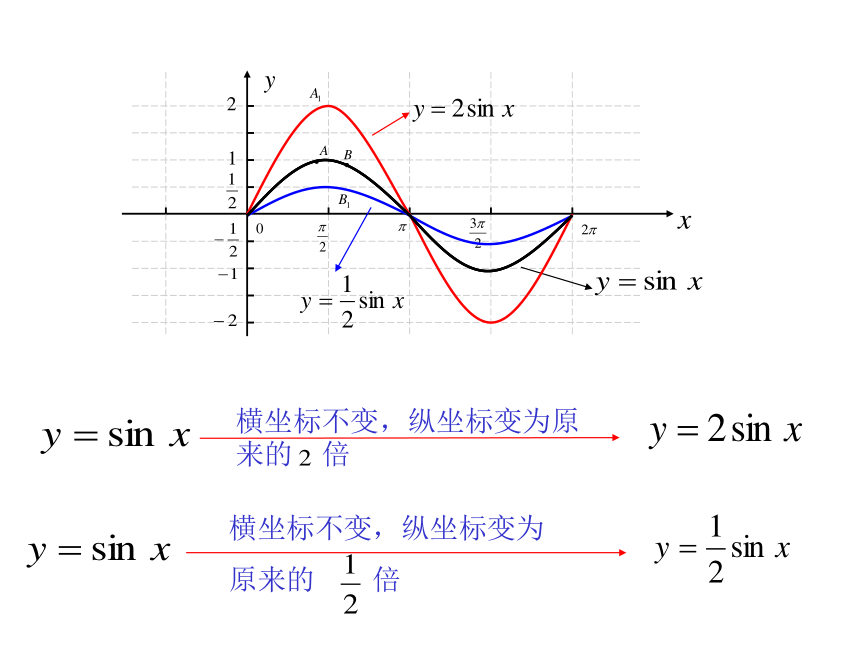
并观察与函数 的图像关系。 2.A对y=Asin(ωx+ ?) 的图象的影响横坐标不变,纵坐标变为
原来的 倍横坐标不变,纵坐标变为原来的 倍 ? 函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当00)的图象与函数y=sinx的图象关系?问题三:作函数 和 的图象,
并观察与函数 的图像关系 。 3. ω对y=Asin(ωx+ ?) 的图象的影响纵坐标不变,横坐标变为原来的 倍纵坐标不变,横坐标变为原来的 倍1-1 ?函数y=sin?x (? >0且?≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当00)的图像与函数y=sinx的图象关系练习:描述下列曲线 可以由正弦曲线如何变换得到变式 :如何由 的图像变换得到 的图像?纵坐标不变,横坐标变为原来的 倍纵坐标不变,横坐标变为原来的 倍一般地, ?函数y=sin(?x +φ) (? >0且?≠1)的图象可以
看作是把 y=sin(x +φ) 的图象上所有点的横坐标
缩短(当?>1时)或伸长(当0倍(纵坐标不变) 而得到的。结论四横坐标伸长为原来的 倍
倍
A
的
来
原
为
长
伸
标
坐
纵
向
右
( <0)
或
向
左
( >0)
平
移
| |函数y=sin(ωx+φ)与y=sinωx图象的关系问题:如何由 的图像变换得到
和 的图像?1-1所有的点向左平移 个单位问题:如何由 的图像变换得到 和 的图像?所有的点向右平移 个单位注意到:结论五函数y=sin(ωx+φ)与y=sinωx图象的关系? 函数y=sin(ωx+φ) 的图象可以看作是把 y=sinωx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移| |个单位而得到的。
巩固练习:1、怎样由函数 的图象得到函数
的图象?3、怎样由函数 的图象得到函数
的图象?2、怎样由函数 的图象得到函数
的图象?例、若函数 表示一个振动
量,求函数的振幅、周期、初相。例、作函数 的简图,并指出它与y=sinx图象的关系。解法一: 先平移后伸缩
2??方法1:先平移后伸缩演示
解法二:先伸缩后平移
2??y=sin2x① 方法2:先伸缩后平移演示12??y=3sinx①y=3sin2x②先伸缩后平移演示2横坐标不变,纵坐标伸长到原来的A倍变换一:从参数 入手向左平移变换二:从参数 入手纵坐标不变,横坐标变为原来的 倍 个单位纵坐标不变,横坐标变为原来的 倍向左平移 个 单 位 由函数 的图像变换得到函数 . 的图像。归纳问题向两边扩展变换三:从参数 入手(口述)巩固练习:
1.已知函数 的图象为C.
(1)为了得到 的图象,只需把C
上的所有点_________________________
1.已知函数 的图象为C.
(2)为了得到 的图象,只需把C
上的所有点______________
1.已知函数 的图象为C.
(3)为了得到 的图象,只需把C
上的所有点______________
2.把函数 的图象向右平移 个单
位,再把所有点的横坐标变为原来的4倍(纵坐标不
变),所得到的函数解析式为___________3.把函数 的图象向右平移 个单
位,再将所有点的横坐标变为原来的3倍(纵坐标不
变),然后又把所有点的纵坐标变为原来的2倍(横
坐标不变),得到了函数 图象,
则函数 解析式为_____________________ 4、若函数 图像上每一个点的纵坐标
不变,横坐标伸长到原来的3倍得到函数 的图
像,再将图像上所有的点向右平移 个单位得
到 的图像,最后将图像上每一点的横坐标不
变,纵坐标伸长到原来的3倍得到 的图像
则 的解析式为课堂小结(上下伸缩变换)(水平伸缩变换)(水平平移变换)1、变换法则:2、题型:函数变换前解析式,变换后解析式及变换法则三
者知其二能求第三。注意:两函数名相同,变换方向要明确。谢谢
y=Asin(?x+?)的图象学习目标:
1、用五点法画函数的图象.
2、能由正弦曲线通过平移、伸缩变换得到的图象,并在这个过程中认识到函数与得联系
重点难点:
1、用五点法列表画函数图象;
2、理解的图象与的图象之间的变换关系.函数y=Asin(ωx+ ?),其中(A>0, ω >0)的图像与函数y=sinx的图象有什么关系呢?例、 作函数 y = 3sin(2 + )的简图五点作图法3、连线:4、根据周期性将作出的简图左右
扩展。能不能通过变换y=sinx的图象作出函数y=Asin(ωx+ ?) 的图象?
问题一:画函数 和 的图
象,并观察与 的图象关系.
1. ?对y=Asin(ωx+ ?) 的图象的影响问题:作函数 及 的图象 作图函数y=sin(x+?)图象与函数y=sinx 的图象关系 ?函数y=sin(x+?) 的图象可以看作是把 y=sinx 的图象上所有的点向左(当? >0时)或向右(当? <0时)平移|? |个单位而得到的.结论一x解:1.列表问题二:作函数 和 的图象,
并观察与函数 的图像关系。 2.A对y=Asin(ωx+ ?) 的图象的影响横坐标不变,纵坐标变为
原来的 倍横坐标不变,纵坐标变为原来的 倍 ? 函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0
并观察与函数 的图像关系 。 3. ω对y=Asin(ωx+ ?) 的图象的影响纵坐标不变,横坐标变为原来的 倍纵坐标不变,横坐标变为原来的 倍1-1 ?函数y=sin?x (? >0且?≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当00)的图像与函数y=sinx的图象关系练习:描述下列曲线 可以由正弦曲线如何变换得到变式 :如何由 的图像变换得到 的图像?纵坐标不变,横坐标变为原来的 倍纵坐标不变,横坐标变为原来的 倍一般地, ?函数y=sin(?x +φ) (? >0且?≠1)的图象可以
看作是把 y=sin(x +φ) 的图象上所有点的横坐标
缩短(当?>1时)或伸长(当0倍(纵坐标不变) 而得到的。结论四横坐标伸长为原来的 倍
倍
A
的
来
原
为
长
伸
标
坐
纵
向
右
( <0)
或
向
左
( >0)
平
移
| |函数y=sin(ωx+φ)与y=sinωx图象的关系问题:如何由 的图像变换得到
和 的图像?1-1所有的点向左平移 个单位问题:如何由 的图像变换得到 和 的图像?所有的点向右平移 个单位注意到:结论五函数y=sin(ωx+φ)与y=sinωx图象的关系? 函数y=sin(ωx+φ) 的图象可以看作是把 y=sinωx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移| |个单位而得到的。
巩固练习:1、怎样由函数 的图象得到函数
的图象?3、怎样由函数 的图象得到函数
的图象?2、怎样由函数 的图象得到函数
的图象?例、若函数 表示一个振动
量,求函数的振幅、周期、初相。例、作函数 的简图,并指出它与y=sinx图象的关系。解法一: 先平移后伸缩
2??方法1:先平移后伸缩演示
解法二:先伸缩后平移
2??y=sin2x① 方法2:先伸缩后平移演示12??y=3sinx①y=3sin2x②先伸缩后平移演示2横坐标不变,纵坐标伸长到原来的A倍变换一:从参数 入手向左平移变换二:从参数 入手纵坐标不变,横坐标变为原来的 倍 个单位纵坐标不变,横坐标变为原来的 倍向左平移 个 单 位 由函数 的图像变换得到函数 . 的图像。归纳问题向两边扩展变换三:从参数 入手(口述)巩固练习:
1.已知函数 的图象为C.
(1)为了得到 的图象,只需把C
上的所有点_________________________
1.已知函数 的图象为C.
(2)为了得到 的图象,只需把C
上的所有点______________
1.已知函数 的图象为C.
(3)为了得到 的图象,只需把C
上的所有点______________
2.把函数 的图象向右平移 个单
位,再把所有点的横坐标变为原来的4倍(纵坐标不
变),所得到的函数解析式为___________3.把函数 的图象向右平移 个单
位,再将所有点的横坐标变为原来的3倍(纵坐标不
变),然后又把所有点的纵坐标变为原来的2倍(横
坐标不变),得到了函数 图象,
则函数 解析式为_____________________ 4、若函数 图像上每一个点的纵坐标
不变,横坐标伸长到原来的3倍得到函数 的图
像,再将图像上所有的点向右平移 个单位得
到 的图像,最后将图像上每一点的横坐标不
变,纵坐标伸长到原来的3倍得到 的图像
则 的解析式为课堂小结(上下伸缩变换)(水平伸缩变换)(水平平移变换)1、变换法则:2、题型:函数变换前解析式,变换后解析式及变换法则三
者知其二能求第三。注意:两函数名相同,变换方向要明确。谢谢
