8.2 一元线性回归模型及其应用 课时作业——2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(word版含答案)
文档属性
| 名称 | 8.2 一元线性回归模型及其应用 课时作业——2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览


文档简介
8.2 一元线性回归模型及其应用-2021-2022学年高二数学人教A版(2019)选择性必修三同步课时作业
1.某产品生产厂家的市场部在对4家商场进行调研时,获得该产品单价x(单位:元)和销售量y(单位:件)之间的四组数据如下表:
x 4 4.5 5.5 6
y 12 11 10 9
用最小二乘法求得y与x之间的线性回归方程为,则的值为( )
A.16.5 B.17 C.17.5 D.18
2.对具有线性相关关系的变量有一组观测数据(),其回归直线方程是,且,则实数的值是( )
A. B. C. D.
3.某商场为了解销售活动中某商品销售量y与活动时间x之间的关系,随机统计了某5次销售活动中的商品销售量与活动时间,并制作了下表:
活动时间x 2 4 5 6 8
销售量y 25 40 60 70 80
由表中数据,销售量y与活动时间x之间具有线性相关关系,算得线性回归方程为,则的值为( )
A.10.75 B.10.25 C.9.75 D.9.25
4.某校课题小组为了研究高一学生数学成绩和物理成绩的线性相关关系,在高一第二学期期中考试后随机抽取了5名同学(记为1,2,3,4,5)数学成绩和物理成绩(满分均为100分)如表所示:
学生代号 1 2 3 4 5
数学成绩x 74 76 76 76 78
物理成绩y 75 75 76 77 77
则y关于x的线性回归方程为( )
A. B. C. D.
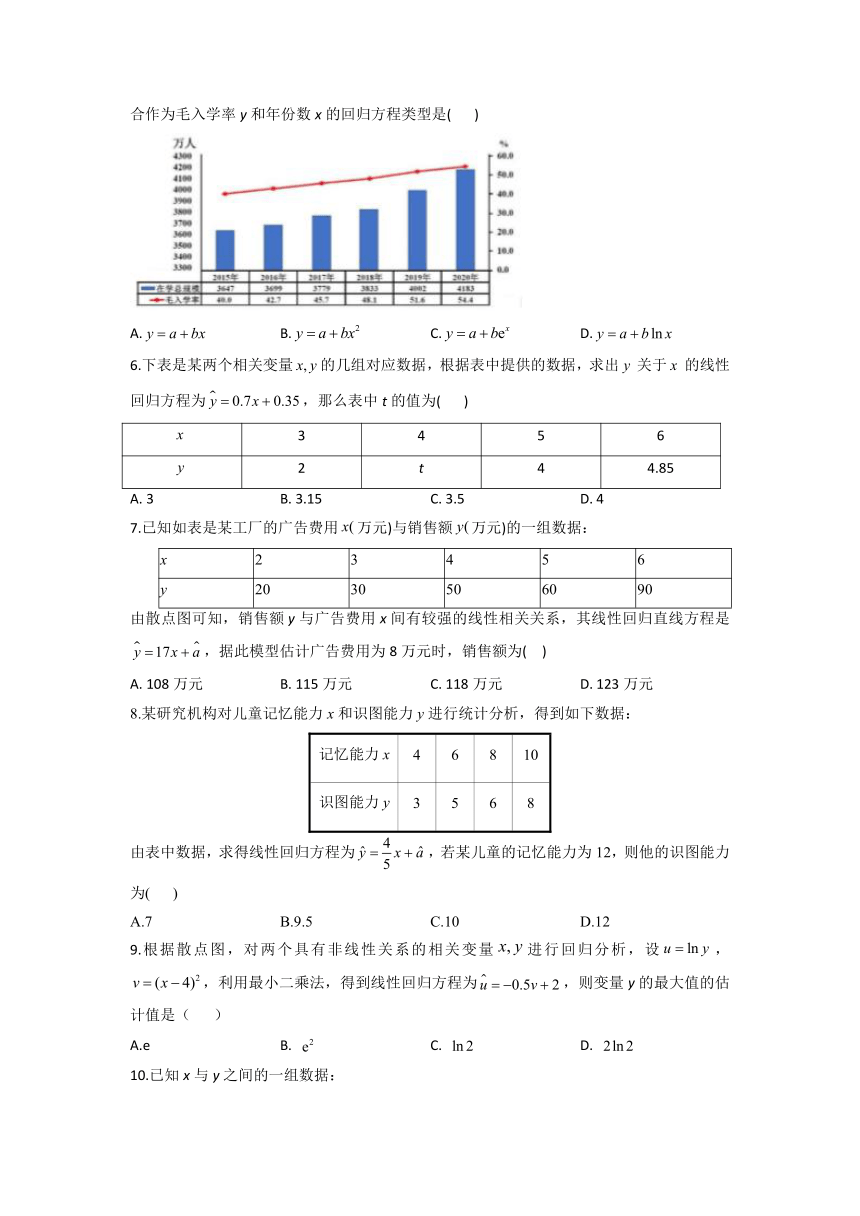
5.2021年8月27日教育部在其网站发布了2020年全国教育事业发展统计公报,其中“十三五”时期全国高等教育在学总规模和毛入学率如下图所示,则下列四个回归方程类型中最适合作为毛入学率y和年份数x的回归方程类型是( )
A. B. C. D.
6.下表是某两个相关变量的几组对应数据,根据表中提供的数据,求出关于的线性回归方程为,那么表中t的值为( )
3 4 5 6
2 t 4 4.85
A. 3 B. 3.15 C. 3.5 D. 4
7.已知如表是某工厂的广告费用万元)与销售额万元)的一组数据:
x 2 3 4 5 6
y 20 30 50 60 90
由散点图可知,销售额y与广告费用x间有较强的线性相关关系,其线性回归直线方程是,据此模型估计广告费用为8万元时,销售额为( )
A. 108万元 B. 115万元 C. 118万元 D. 123万元
8.某研究机构对儿童记忆能力x和识图能力y进行统计分析,得到如下数据:
记忆能力x 4 6 8 10
识图能力y 3 5 6 8
由表中数据,求得线性回归方程为,若某儿童的记忆能力为12,则他的识图能力为( )
A.7 B.9.5 C.10 D.12
9.根据散点图,对两个具有非线性关系的相关变量进行回归分析,设,,利用最小二乘法,得到线性回归方程为,则变量y的最大值的估计值是( )
A.e B. C. D.
10.已知x与y之间的一组数据:
x 0 1 2 3
y 1 3 5 7
则y与x的线性回归方程必过( )
A. B. C. D.
11.为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,得到5组数据根据收集到的数据可知,由最小二乘法求得回归直线方程为,则_____________.
12.高二某班数学学习小组成员最近研究的椭圆的问题数x与抛物线的问题数y之间有如下的对应数据:
1 2 3 4 5
2 4 5 5
若用最小二乘法求得线性回归方程是,则表中的m是___________.
13.若某地的财政收入与支出满足线性回归方程(单位:亿元),其中,,.若今年该地区财政收入为10亿元,则年支出预计不会超过________亿元.
14.共享单车以低碳、环保、节能、健康的理念,成为解决市民出行“最后一公里”的有力手段.某公司调研部门统计了最近5个季度本公司的共享单车使用次数(万次),结果如下:
季度序号x 1 2 3 4 5
使用次数y(万次) 1 1.2 1.5 1.8 2.2
(1)(i)根据上表,画岀散点图并根据所画散点图,判断能否用线性回归模型拟合使用次数y与季度序号x之间的关系,如果能,求出y关于x的线性回归方程;如果不能,请说明理由.
(ii)如果你是公司主管领导,你会在下一季度向市场增加投放共享单车吗?请说明理由.
(2)为进一步开拓市场做准备,公司目前接受报价的有两款车型:A型单车每辆500元,第一年收入500元,以后逐年递减80元;B型单车每辆300元,第一年收入500元,以后逐年递减100元.经市场调研,两款车型使用寿命频数统计如下表:
车型\使用寿命 1年 2年 3年 4年 总计
A 10 20 30 40 100
B 10 35 30 25 100
不考虑除釆购成本以外的其它成本,假设毎辆单车的使用寿命都是整数年,用频率估计概率,以1辆单车所产生的利润的数学期望为决策依据,如果你是公司负责人,会选择哪款车型?
参考数据:,.
参考公式:,.
答案以及解析
1.答案:C
解析:由题意,,
,
线性回归方程,
,
.
故选C.
2.答案:A
解析:因为,,
所以,所以样本中心点的坐标为,
代入回归直线方程得,解得,故选A.
3.答案:C
解析:线性回归方程过样本中心点,
,
,
.
故选:C.
4.答案:C
解析:由表格中的数据,可得,,
即数据的样本中心,
因为满足回归直线方程,结合选项可得,
即y关于x的线性回归方程为:,
故选:C.
5.答案:A
解析:根据图象可知,函数图象随着自变量的变大,函数值增长速度基本不变,再由图象的形状结合选项,可判定函数符合要求.故选:A.
6.答案:B
解析:,,中心点过,即,解得.故选B.
7.答案:C
解析:由表格的数据可得,,,
∵线性回归直线方程是,,,当时,,
故广告费为8万元时,销售额累计为118万元.
故选:C.
8.答案:B
解析:由表中数据得,,
由在直线上,得,即线性回归方程为
当时,即他的识图能力为9.5.
9.答案:B
解析:依题意,模拟函数为,所以最大值为
10.答案:D
解析:根据题意知,变量;
分别求出它们的平均值为;.
所以样本中心点为,即回归方程必过点.
故选D.
11.答案:100
解析:由于线性回归直线方程过样本中心点,设样本中心点为,
由题意,故,
代入计算可得:.
故.
12.答案:4
解析:,
,
回归直线经过样本中心,可得,解得.
故答案为:4.
13.答案:10
解析:由题意得财政收入与支出满足线性回归方程为,其中,
当时,,
因为 ,所以,
所以今年该地区财政收入为10亿元,则年支出预计不会超过10亿元,故答案为:10
14.答案: (1),具体见解析
(2) 1辆B型单车纯利润的数学期望大于1辆A型单车的,所以选择B型单车
解析: (1)(i)散点图如图所示:
根据散点图,可以用线性回归模型拟合使用次数y与次季度序号x之间的关系,
设回归方程为,
则,
由,,得,
所以y关于x的线性回归方程为.
(ii)参考一:下一季度可以向市场增加投放共享单车,理由:
①由(i)中散点图判断可预估下季度市场对本公司单车使用次数会持续上涨;
②由(i)中使用次数y关于季度序号x的线性回归方程可知,下季度市场对本公司单车下一季度的使用次数会持续上涨0.3万次左右,因此需要向市场增加投放共享单车.
参考二:下一季度可以先不向市场增加投放共享单车,理由:
题中只给岀了使用次数这一方面的数据,是否增加投放共享单车还要考察单车的使用率高低,单车的区域分布是否合理,单车使用后的回收与分配是否及时等等因素,这些都会影响投放单车的决策,因此要进行进一步调查过后才能决定.
(2)设1辆A型单车产生的毛利润为随机变量,则的所有可能取值为500,920,1260,1520,
用频率估计概率,则1辆A型单车产生毛利润的分布列为
毛利润 500 920 1260 1520
概率
则1辆A型单车毛利润的数学期望,故1辆A型单车纯利润的数字期望为
设1辆B型单车产生的毛利润为随机变量,则的所有可能取值为500,900,1200,1400,
用频率估计概率,则1辆B型单车产生毛利润的分布列为
毛利润 500 900 1200 1400
概率
则1辆B型单车毛利润的数学期望,故1辆B型单车纯利润的数学期望为,
因为1辆B型单车纯利润的数学期望大于1辆A型单车的,所以选择B型单车.
1.某产品生产厂家的市场部在对4家商场进行调研时,获得该产品单价x(单位:元)和销售量y(单位:件)之间的四组数据如下表:
x 4 4.5 5.5 6
y 12 11 10 9
用最小二乘法求得y与x之间的线性回归方程为,则的值为( )
A.16.5 B.17 C.17.5 D.18
2.对具有线性相关关系的变量有一组观测数据(),其回归直线方程是,且,则实数的值是( )
A. B. C. D.
3.某商场为了解销售活动中某商品销售量y与活动时间x之间的关系,随机统计了某5次销售活动中的商品销售量与活动时间,并制作了下表:
活动时间x 2 4 5 6 8
销售量y 25 40 60 70 80
由表中数据,销售量y与活动时间x之间具有线性相关关系,算得线性回归方程为,则的值为( )
A.10.75 B.10.25 C.9.75 D.9.25
4.某校课题小组为了研究高一学生数学成绩和物理成绩的线性相关关系,在高一第二学期期中考试后随机抽取了5名同学(记为1,2,3,4,5)数学成绩和物理成绩(满分均为100分)如表所示:
学生代号 1 2 3 4 5
数学成绩x 74 76 76 76 78
物理成绩y 75 75 76 77 77
则y关于x的线性回归方程为( )
A. B. C. D.
5.2021年8月27日教育部在其网站发布了2020年全国教育事业发展统计公报,其中“十三五”时期全国高等教育在学总规模和毛入学率如下图所示,则下列四个回归方程类型中最适合作为毛入学率y和年份数x的回归方程类型是( )
A. B. C. D.
6.下表是某两个相关变量的几组对应数据,根据表中提供的数据,求出关于的线性回归方程为,那么表中t的值为( )
3 4 5 6
2 t 4 4.85
A. 3 B. 3.15 C. 3.5 D. 4
7.已知如表是某工厂的广告费用万元)与销售额万元)的一组数据:
x 2 3 4 5 6
y 20 30 50 60 90
由散点图可知,销售额y与广告费用x间有较强的线性相关关系,其线性回归直线方程是,据此模型估计广告费用为8万元时,销售额为( )
A. 108万元 B. 115万元 C. 118万元 D. 123万元
8.某研究机构对儿童记忆能力x和识图能力y进行统计分析,得到如下数据:
记忆能力x 4 6 8 10
识图能力y 3 5 6 8
由表中数据,求得线性回归方程为,若某儿童的记忆能力为12,则他的识图能力为( )
A.7 B.9.5 C.10 D.12
9.根据散点图,对两个具有非线性关系的相关变量进行回归分析,设,,利用最小二乘法,得到线性回归方程为,则变量y的最大值的估计值是( )
A.e B. C. D.
10.已知x与y之间的一组数据:
x 0 1 2 3
y 1 3 5 7
则y与x的线性回归方程必过( )
A. B. C. D.
11.为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,得到5组数据根据收集到的数据可知,由最小二乘法求得回归直线方程为,则_____________.
12.高二某班数学学习小组成员最近研究的椭圆的问题数x与抛物线的问题数y之间有如下的对应数据:
1 2 3 4 5
2 4 5 5
若用最小二乘法求得线性回归方程是,则表中的m是___________.
13.若某地的财政收入与支出满足线性回归方程(单位:亿元),其中,,.若今年该地区财政收入为10亿元,则年支出预计不会超过________亿元.
14.共享单车以低碳、环保、节能、健康的理念,成为解决市民出行“最后一公里”的有力手段.某公司调研部门统计了最近5个季度本公司的共享单车使用次数(万次),结果如下:
季度序号x 1 2 3 4 5
使用次数y(万次) 1 1.2 1.5 1.8 2.2
(1)(i)根据上表,画岀散点图并根据所画散点图,判断能否用线性回归模型拟合使用次数y与季度序号x之间的关系,如果能,求出y关于x的线性回归方程;如果不能,请说明理由.
(ii)如果你是公司主管领导,你会在下一季度向市场增加投放共享单车吗?请说明理由.
(2)为进一步开拓市场做准备,公司目前接受报价的有两款车型:A型单车每辆500元,第一年收入500元,以后逐年递减80元;B型单车每辆300元,第一年收入500元,以后逐年递减100元.经市场调研,两款车型使用寿命频数统计如下表:
车型\使用寿命 1年 2年 3年 4年 总计
A 10 20 30 40 100
B 10 35 30 25 100
不考虑除釆购成本以外的其它成本,假设毎辆单车的使用寿命都是整数年,用频率估计概率,以1辆单车所产生的利润的数学期望为决策依据,如果你是公司负责人,会选择哪款车型?
参考数据:,.
参考公式:,.
答案以及解析
1.答案:C
解析:由题意,,
,
线性回归方程,
,
.
故选C.
2.答案:A
解析:因为,,
所以,所以样本中心点的坐标为,
代入回归直线方程得,解得,故选A.
3.答案:C
解析:线性回归方程过样本中心点,
,
,
.
故选:C.
4.答案:C
解析:由表格中的数据,可得,,
即数据的样本中心,
因为满足回归直线方程,结合选项可得,
即y关于x的线性回归方程为:,
故选:C.
5.答案:A
解析:根据图象可知,函数图象随着自变量的变大,函数值增长速度基本不变,再由图象的形状结合选项,可判定函数符合要求.故选:A.
6.答案:B
解析:,,中心点过,即,解得.故选B.
7.答案:C
解析:由表格的数据可得,,,
∵线性回归直线方程是,,,当时,,
故广告费为8万元时,销售额累计为118万元.
故选:C.
8.答案:B
解析:由表中数据得,,
由在直线上,得,即线性回归方程为
当时,即他的识图能力为9.5.
9.答案:B
解析:依题意,模拟函数为,所以最大值为
10.答案:D
解析:根据题意知,变量;
分别求出它们的平均值为;.
所以样本中心点为,即回归方程必过点.
故选D.
11.答案:100
解析:由于线性回归直线方程过样本中心点,设样本中心点为,
由题意,故,
代入计算可得:.
故.
12.答案:4
解析:,
,
回归直线经过样本中心,可得,解得.
故答案为:4.
13.答案:10
解析:由题意得财政收入与支出满足线性回归方程为,其中,
当时,,
因为 ,所以,
所以今年该地区财政收入为10亿元,则年支出预计不会超过10亿元,故答案为:10
14.答案: (1),具体见解析
(2) 1辆B型单车纯利润的数学期望大于1辆A型单车的,所以选择B型单车
解析: (1)(i)散点图如图所示:
根据散点图,可以用线性回归模型拟合使用次数y与次季度序号x之间的关系,
设回归方程为,
则,
由,,得,
所以y关于x的线性回归方程为.
(ii)参考一:下一季度可以向市场增加投放共享单车,理由:
①由(i)中散点图判断可预估下季度市场对本公司单车使用次数会持续上涨;
②由(i)中使用次数y关于季度序号x的线性回归方程可知,下季度市场对本公司单车下一季度的使用次数会持续上涨0.3万次左右,因此需要向市场增加投放共享单车.
参考二:下一季度可以先不向市场增加投放共享单车,理由:
题中只给岀了使用次数这一方面的数据,是否增加投放共享单车还要考察单车的使用率高低,单车的区域分布是否合理,单车使用后的回收与分配是否及时等等因素,这些都会影响投放单车的决策,因此要进行进一步调查过后才能决定.
(2)设1辆A型单车产生的毛利润为随机变量,则的所有可能取值为500,920,1260,1520,
用频率估计概率,则1辆A型单车产生毛利润的分布列为
毛利润 500 920 1260 1520
概率
则1辆A型单车毛利润的数学期望,故1辆A型单车纯利润的数字期望为
设1辆B型单车产生的毛利润为随机变量,则的所有可能取值为500,900,1200,1400,
用频率估计概率,则1辆B型单车产生毛利润的分布列为
毛利润 500 900 1200 1400
概率
则1辆B型单车毛利润的数学期望,故1辆B型单车纯利润的数学期望为,
因为1辆B型单车纯利润的数学期望大于1辆A型单车的,所以选择B型单车.
