6.3利用导数解决实际问题同步课时作业-2021-2022学年高二下学期数学人教B版(2019)选择性必修三册(word含解析)
文档属性
| 名称 | 6.3利用导数解决实际问题同步课时作业-2021-2022学年高二下学期数学人教B版(2019)选择性必修三册(word含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 407.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览




文档简介
6.3 利用导数解决实际问题-2021-2022学年高二数学人教B版(2019)选择性必修三同步课时作业
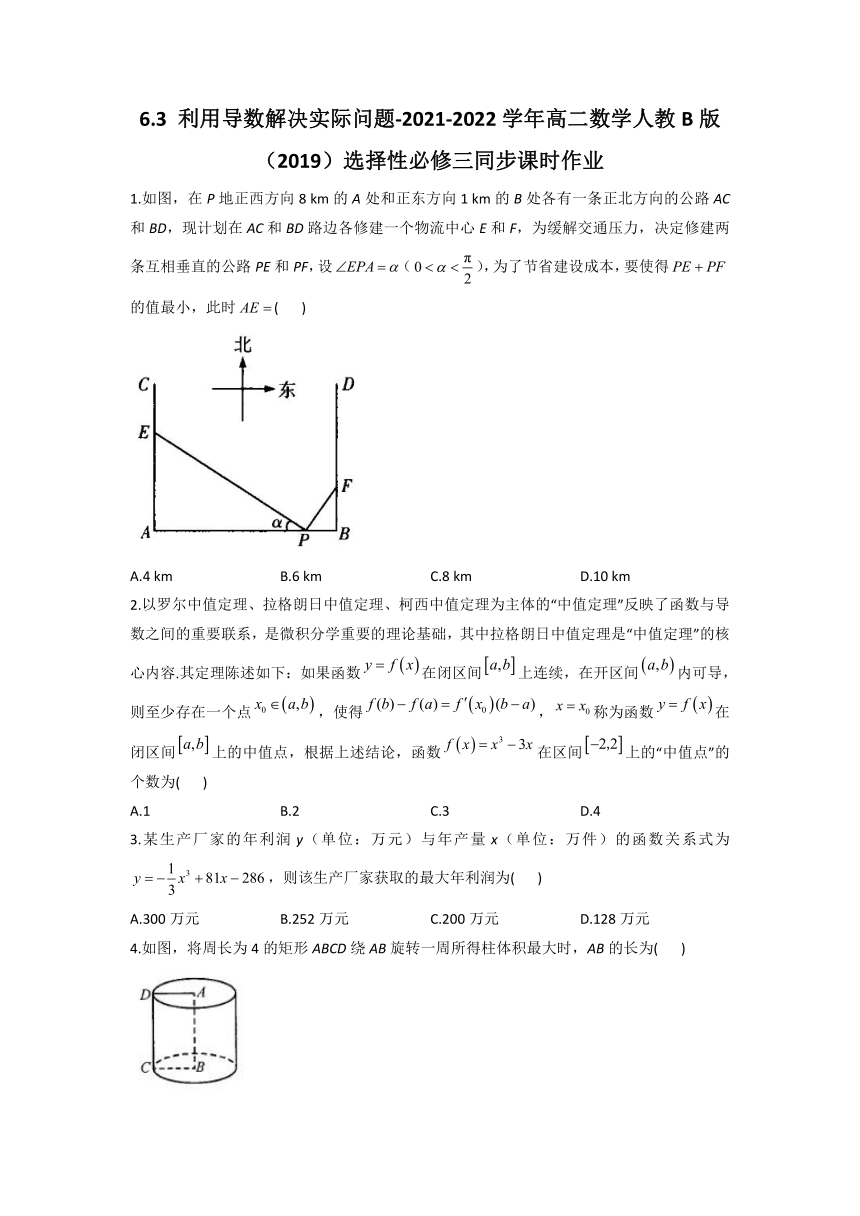
1.如图,在P地正西方向8 km的A处和正东方向1 km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设(),为了节省建设成本,要使得的值最小,此时( )
A.4 km B.6 km C.8 km D.10 km
2.以罗尔中值定理、拉格朗日中值定理、柯西中值定理为主体的“中值定理”反映了函数与导数之间的重要联系,是微积分学重要的理论基础,其中拉格朗日中值定理是“中值定理”的核心内容.其定理陈述如下:如果函数在闭区间上连续,在开区间内可导,则至少存在一个点,使得,称为函数在闭区间上的中值点,根据上述结论,函数在区间上的“中值点”的个数为( )
A.1 B.2 C.3 D.4
3.某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为,则该生产厂家获取的最大年利润为( )
A.300万元 B.252万元 C.200万元 D.128万元
4.如图,将周长为4的矩形ABCD绕AB旋转一周所得柱体积最大时,AB的长为( )
A. B. C. D.1
5.用长为30 cm的钢条围成一个长方体形状的框架(即12条棱长的总和为30 cm),要求长方体的长与宽之比为,则该长方体的最大体积是( )
A.24 B.15 C.12 D.6
6.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为,则使该生产厂家获得最大年利润的年产量为( )
A.13万件 B.11万件 C.9万件 D.7万件
7.某厂生产x万件某产品的总成本为C(x)万元,且.已知产品单价(单位:元)的平方与x成反比,且生产100万件这样的产品时,单价为50元,则为使总利润y(单位:万元)最大,产量应定为( )
A.23万件 B.25万件 C.50万件 D.75万件
8.给出定义:若函数在D上可导,即存在,且导函数在D上也可导,则称在D上存在二阶导函数,记,若在D上恒成立,则称在D上为凸函数.以下四个函数在上不是凸函数的是( )
A. B.
C. D.
9.定义方程的实数根为函数的“新驻点”,若函数,,的“新驻点”分别为a,b,c,则a,b,c的大小关系为( )
A. B. C. D.
10.用边长为18cm的正方形铁皮做一个无盖的铁盒,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒,当铁盒的容积最大时,截去的小正方形的边长为( )
A.1 cm B.2 cm C.3 cm D.4 cm
11.已知正四棱锥内接于半径为1的球,则当此正四棱锥的体积最大时,其高为________________.
12.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为,则使该生产厂家获取最大年利润的年产量为__________万件.
13.由曲线,直线所围成的封闭的图形面积为_________.
14.经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足(其中,a为正常数).已知生产该产品还需投入成本万元(不含促销费用),每一件产品的销售价格定为元,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.
答案以及解析
1.答案:A
解析:因为,,所以,在中,,在中,,则.设,,则,令,则,当时,,当时,,所以当时,取得最小值,此时,故选A.
2.答案:B
解析:由题意,函数,可得,,,
由,可得,即,
解得,所以在区间上的“中值点”的个数为2.
3.答案:C
解析:由题意,函数,所以,当时,;当时,,所以当时,y有最大值,此时最大年利润为200万元.
4.答案:B
解析:设,则,所以,,则,由,得,解得;由,得,解得,所以在区间上单调递增,在区间上单调递减,所以当,即,时,取得最大值.
5.答案:B
解析:设该长方体的宽是x m,则由题意知,其长是,高是,其中,则该长方体的体积,,由,得,且当时,;当时,,即体积函数在处取得极大值,也是函数在定义域上的最大值,所以该长方体体积的最大值是15.
6.答案:C
解析:令导数,解得;
令导数,解得,
所以函数在区间上是增函数,在区间上是减函数,
所以在处取得极大值,也是最大值,故选C.
7.答案:B
解析:设产品单价为a元,,则,,,即,总利润,,令,得,则当时,;当时,.当产量定为25万件时,总利润最大.
8.答案:B
解析:对于,,,当时,恒成立,故为凸函数,排除A;对于,,,当时,,故不为凸函数;对于,,,当时,恒成立,故为凸函数,排除C;对于,,,当时,恒成立,故为凸函数,排除D.故选B.
9.答案:B
解析:,,.解方程,即,得,即;解方程,即,在同一坐标系中画出函数,的图象(图略),可得,即;解方程,即,得,即,所以.
10.答案:C
解析:设截去的小正方形的边长为x cm,
则铁盒的底面边长为,高为x cm,
所以铁盒的容积,
所以,
所以V在上单调递增,在上单调递减,
所以当时,V取得最大值.
11.答案:
解析:由球的几何性质可设四棱锥的高为h,从而,令,则,当时,,单调递增;当时,,单调递减,所以当时,取得最大值,即体积最大.
12.答案:9
解析:由,得.令,得(舍去),,所以当时,,函数为增函数;当时,,函数为减函数,故当时,函数有最大值为(万元),即使该生产厂家获取最大年利润的年产量为9万件.
13.答案:
解析: 依题意,由解得,
∴封闭的图形面积为.
故答案为:.
14.答案:(1)().
(2)当时,促销费用投入1万元,厂家的利润最大为13万元;
当时,促销费用投入a万元,厂家的利润为.
解析:(1)由题意知,,
将代入化简得:().
(2),
(ⅰ)当时,
①当时,,所以函数在上单调递增,
②当时,,所以函数在上单调递减,
从而促销费用投入1万元时,厂家的利润最大;
(ⅱ)当时,因为函数在上单调递增,
所以在上单调递增,故当时,函数有最大值,
即促销费用投入a万元时,厂家的利润最大.
综上:当时,促销费用投入1万元,厂家的利润最大,为万元;
当时,促销费用投入a万元,厂家的利润最大,为万元.
1.如图,在P地正西方向8 km的A处和正东方向1 km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设(),为了节省建设成本,要使得的值最小,此时( )
A.4 km B.6 km C.8 km D.10 km
2.以罗尔中值定理、拉格朗日中值定理、柯西中值定理为主体的“中值定理”反映了函数与导数之间的重要联系,是微积分学重要的理论基础,其中拉格朗日中值定理是“中值定理”的核心内容.其定理陈述如下:如果函数在闭区间上连续,在开区间内可导,则至少存在一个点,使得,称为函数在闭区间上的中值点,根据上述结论,函数在区间上的“中值点”的个数为( )
A.1 B.2 C.3 D.4
3.某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为,则该生产厂家获取的最大年利润为( )
A.300万元 B.252万元 C.200万元 D.128万元
4.如图,将周长为4的矩形ABCD绕AB旋转一周所得柱体积最大时,AB的长为( )
A. B. C. D.1
5.用长为30 cm的钢条围成一个长方体形状的框架(即12条棱长的总和为30 cm),要求长方体的长与宽之比为,则该长方体的最大体积是( )
A.24 B.15 C.12 D.6
6.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为,则使该生产厂家获得最大年利润的年产量为( )
A.13万件 B.11万件 C.9万件 D.7万件
7.某厂生产x万件某产品的总成本为C(x)万元,且.已知产品单价(单位:元)的平方与x成反比,且生产100万件这样的产品时,单价为50元,则为使总利润y(单位:万元)最大,产量应定为( )
A.23万件 B.25万件 C.50万件 D.75万件
8.给出定义:若函数在D上可导,即存在,且导函数在D上也可导,则称在D上存在二阶导函数,记,若在D上恒成立,则称在D上为凸函数.以下四个函数在上不是凸函数的是( )
A. B.
C. D.
9.定义方程的实数根为函数的“新驻点”,若函数,,的“新驻点”分别为a,b,c,则a,b,c的大小关系为( )
A. B. C. D.
10.用边长为18cm的正方形铁皮做一个无盖的铁盒,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒,当铁盒的容积最大时,截去的小正方形的边长为( )
A.1 cm B.2 cm C.3 cm D.4 cm
11.已知正四棱锥内接于半径为1的球,则当此正四棱锥的体积最大时,其高为________________.
12.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为,则使该生产厂家获取最大年利润的年产量为__________万件.
13.由曲线,直线所围成的封闭的图形面积为_________.
14.经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足(其中,a为正常数).已知生产该产品还需投入成本万元(不含促销费用),每一件产品的销售价格定为元,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.
答案以及解析
1.答案:A
解析:因为,,所以,在中,,在中,,则.设,,则,令,则,当时,,当时,,所以当时,取得最小值,此时,故选A.
2.答案:B
解析:由题意,函数,可得,,,
由,可得,即,
解得,所以在区间上的“中值点”的个数为2.
3.答案:C
解析:由题意,函数,所以,当时,;当时,,所以当时,y有最大值,此时最大年利润为200万元.
4.答案:B
解析:设,则,所以,,则,由,得,解得;由,得,解得,所以在区间上单调递增,在区间上单调递减,所以当,即,时,取得最大值.
5.答案:B
解析:设该长方体的宽是x m,则由题意知,其长是,高是,其中,则该长方体的体积,,由,得,且当时,;当时,,即体积函数在处取得极大值,也是函数在定义域上的最大值,所以该长方体体积的最大值是15.
6.答案:C
解析:令导数,解得;
令导数,解得,
所以函数在区间上是增函数,在区间上是减函数,
所以在处取得极大值,也是最大值,故选C.
7.答案:B
解析:设产品单价为a元,,则,,,即,总利润,,令,得,则当时,;当时,.当产量定为25万件时,总利润最大.
8.答案:B
解析:对于,,,当时,恒成立,故为凸函数,排除A;对于,,,当时,,故不为凸函数;对于,,,当时,恒成立,故为凸函数,排除C;对于,,,当时,恒成立,故为凸函数,排除D.故选B.
9.答案:B
解析:,,.解方程,即,得,即;解方程,即,在同一坐标系中画出函数,的图象(图略),可得,即;解方程,即,得,即,所以.
10.答案:C
解析:设截去的小正方形的边长为x cm,
则铁盒的底面边长为,高为x cm,
所以铁盒的容积,
所以,
所以V在上单调递增,在上单调递减,
所以当时,V取得最大值.
11.答案:
解析:由球的几何性质可设四棱锥的高为h,从而,令,则,当时,,单调递增;当时,,单调递减,所以当时,取得最大值,即体积最大.
12.答案:9
解析:由,得.令,得(舍去),,所以当时,,函数为增函数;当时,,函数为减函数,故当时,函数有最大值为(万元),即使该生产厂家获取最大年利润的年产量为9万件.
13.答案:
解析: 依题意,由解得,
∴封闭的图形面积为.
故答案为:.
14.答案:(1)().
(2)当时,促销费用投入1万元,厂家的利润最大为13万元;
当时,促销费用投入a万元,厂家的利润为.
解析:(1)由题意知,,
将代入化简得:().
(2),
(ⅰ)当时,
①当时,,所以函数在上单调递增,
②当时,,所以函数在上单调递减,
从而促销费用投入1万元时,厂家的利润最大;
(ⅱ)当时,因为函数在上单调递增,
所以在上单调递增,故当时,函数有最大值,
即促销费用投入a万元时,厂家的利润最大.
综上:当时,促销费用投入1万元,厂家的利润最大,为万元;
当时,促销费用投入a万元,厂家的利润最大,为万元.
