5.1.2导数的概念及其意义分类练习-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(word含解析)
文档属性
| 名称 | 5.1.2导数的概念及其意义分类练习-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 502.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 15:05:59 | ||
图片预览



文档简介
人教版(2019)5.1导数的概念及其意义
平均变化率
1.(2021·江苏·高二课时练习)一物体的运动方程是,则t在内的平均速度为( )
A.0.41 B.4.1 C.0.3 D.3
2.(2021·辽宁·大连八中期中)函数,在[0,2]上的平均变化率分别记为,,则下列结论正确的是( )
A. B. C. D.,的大小无法确定
瞬时变化率(导数)
1.(2021·全国·高二同步练习)已知物体做自由落体的运动方程为,且无限趋近于0时,无限趋近于9.8m/s.那么关于9.8m/s正确的说法是( ).
A.物体在0~1s这一段时间内的速度
B.物体在这一段时间内的速度
C.物体在1s这一时刻的速度
D.物体从1s到这一段时间内的平均速度
2.(2020·全国·高二练习)某物体的运动路程s(单位:)与时间t(单位:)的关系可用函数s(t)=t3-2表示,则此物体在t0时的瞬时速度为27,则t0=________.
3.(2021·全国·高二课时练习)若函数在处可导,则的结果( ).
A.与,h均无关 B.仅与有关,而与h无关
C.仅与h有关,而与无关 D.与,h均有关
4.(原创)已知函数,求在处的导数.
5.(2021·河北·藁城新冀明中学高二阶段练习)已知,则___________.
导数的几何意义
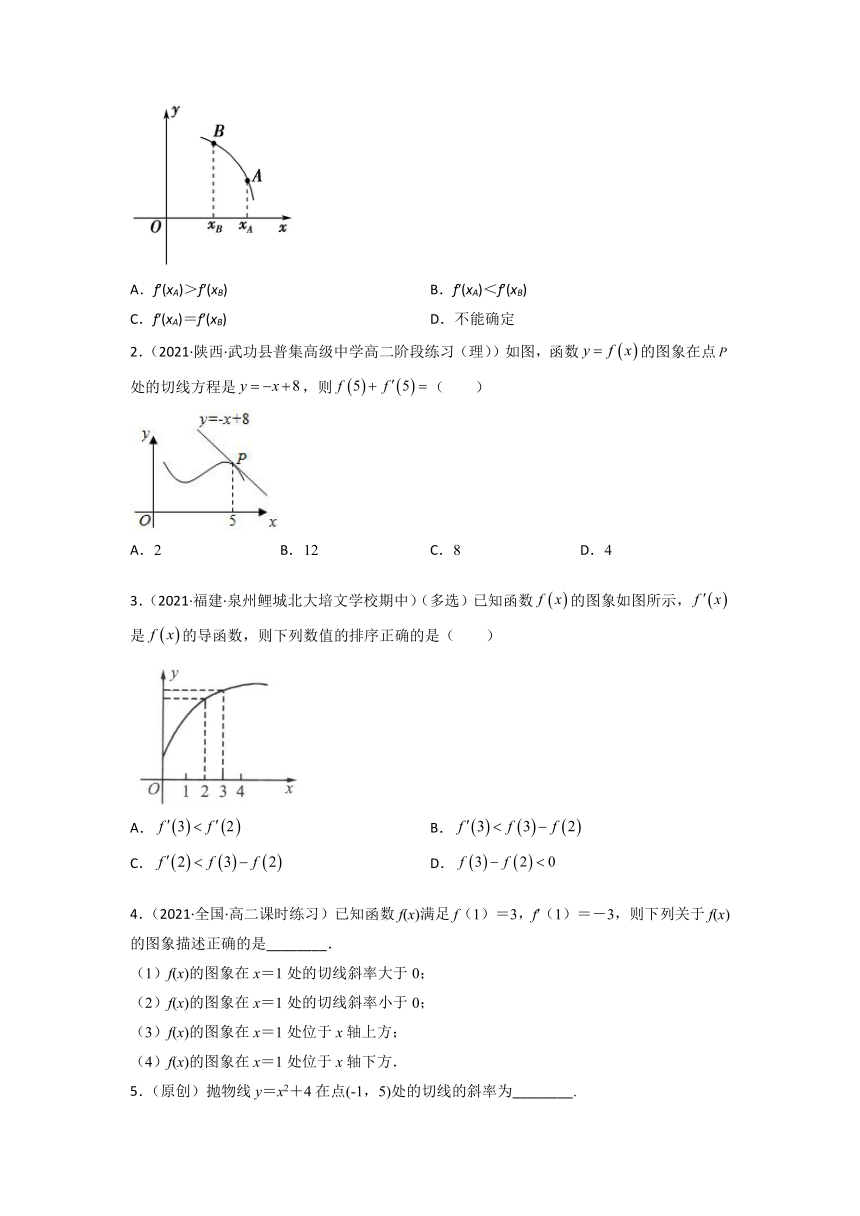
1.(2021·全国·高二课时练习)已知的图象如图所示,则与的大小关系是( )
A.f′(xA)>f′(xB) B.f′(xA)<f′(xB)
C.f′(xA)=f′(xB) D.不能确定
2.(2021·陕西·武功县普集高级中学高二阶段练习(理))如图,函数的图象在点处的切线方程是,则( )
A.2 B.12 C.8 D.4
3.(2021·福建·泉州鲤城北大培文学校期中)(多选)已知函数的图象如图所示,是的导函数,则下列数值的排序正确的是( )
A. B.
C. D.
4.(2021·全国·高二课时练习)已知函数f(x)满足f(1)=3,f′(1)=-3,则下列关于f(x)的图象描述正确的是________.
(1)f(x)的图象在x=1处的切线斜率大于0;
(2)f(x)的图象在x=1处的切线斜率小于0;
(3)f(x)的图象在x=1处位于x轴上方;
(4)f(x)的图象在x=1处位于x轴下方.
5.(原创)抛物线y=x2+4在点(-1,5)处的切线的斜率为________.
6.(2021·全国·高二课时练习)求抛物线f(x)=x2-x在点(2,2)处的切线方程.
巩固提升
一、单选题
1.设函数y=f(x)=x2-1,当自变量x由1变为1.1时,函数的平均变化率为( )
A.2.1 B.1.1 C.2 D.0
2.函数f(x)的图象如图所示,则( )
A.f′(1)>f′(2)>f′(3) B.f′(2)>f′(1)>f′(3)
C.f′(3)>f′(2)>f′(1) D.f′(3)>f′(1)>f′(2)
3.设为可导函数,且,则曲线在点处的切线斜率为( )
A.2 B.-1 C.1 D.
4.函数在点处的切线方程是,则( )
A.2 B.3 C.4 D.5
5.已知抛物线上一点P,则在点P处的切线的倾斜角为( )
A.30° B.45°
C.135° D.165°
6.曲线y=x+上任意一点P处的切线斜率为k,则k的取值范围是( )
A.(-∞,-1) B.(-1,1)
C.(-∞,1) D.(1,+∞)
二、多选题
7.已知函数的图象如下图,则函数在区间上的平均变化率情况是( )
A.在区间上的平均变化率最小
B.在区间上的平均变化率大于0
C.在区间上的平均变化率比上的大
D.在区间上的平均变化率最大
8.下列说法正确的是( )
A.若不存在,则曲线在点处也可能有切线
B.若曲线在点处有切线,则必存在
C.若不存在,则曲线在点处的切线斜率不存在
D.若曲线在点处没有切线,则有可能存在
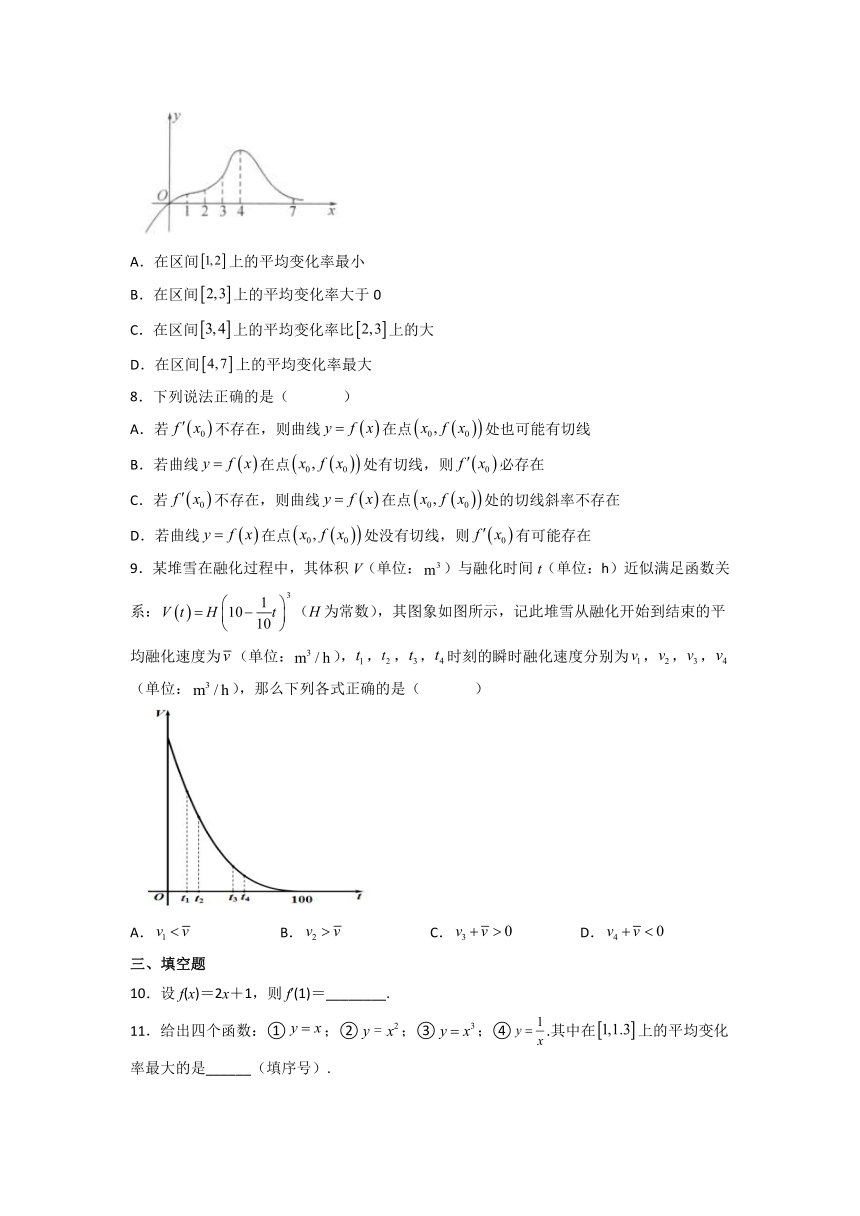
9.某堆雪在融化过程中,其体积V(单位:)与融化时间t(单位:h)近似满足函数关系:(H为常数),其图象如图所示,记此堆雪从融化开始到结束的平均融化速度为(单位:),,,,时刻的瞬时融化速度分别为,,,(单位:),那么下列各式正确的是( )
A. B. C. D.
三、填空题
10.设f(x)=2x+1,则f′(1)=________.
11.给出四个函数:①;②;③;④.其中在上的平均变化率最大的是______(填序号).
12.若函数在处的导数是8,则________.
13.为了评估某种治疗肺炎药物的疗效,现有关部门对该药物在人体血管中的药物浓度进行测量.设该药物在人体血管中药物浓度与时间的关系为,甲、乙两人服用该药物后,血管中药物浓度随时间变化的关系如下图所示.
给出下列四个结论:
① 在时刻,甲、乙两人血管中的药物浓度相同;
② 在时刻,甲、乙两人血管中药物浓度的瞬时变化率相同;
③ 在这个时间段内,甲、乙两人血管中药物浓度的平均变化率相同;
④ 在,两个时间段内,甲血管中药物浓度的平均变化率不相同.
其中所有正确结论的序号是_____.
四、解答题
14.已知某产品的总成本函数为,总成本函数在处导数称为在处的边际成本,用表示.求边际成本并说明它的实际意义.
15.在曲线E:上求出满足下列条件的点P的坐标.
(1)在点P处曲线E的切线平行于直线;
(2)在点P处曲线E的切线的倾斜角是135°.
16.若曲线在点A处的切线方程为,且点A在直线(其中,)上,求的最小值.
参考答案
平均变化率
1.B
,
故选:B
2.A
,,故.
故选:A.
瞬时变化率(导数)
1.C
由平均速度的概念,表示的是这一段时间内的平均速度,其极限值即,表示这一时刻的瞬时速度.
故选:C
2.3
解:由,得,
由题意得,解得.
因为,故.
故答案为:3
3.B
解:因为,
所以结果仅与有关,而与h无关,
故选:B.
4.6.
当自变量在处的改变量为时,平均变化率
.
化简,当无限接近于0时,无限接近于6,
因此
5.-8
解:令,
因为.
所以,
故答案为:.
导数的几何意义
1.B
由导数的几何意义可知,f′(xA),f′(xB)分别是切线在点A、B处切线的斜率,
由图象可知f′(xA)<f′(xB).
故选:B
2.A
解:根据题意,函数的图象在点处的切线方程是,
切点的横坐标为5,
则有(5),(5),
则(5)(5);
故选:A.
3.AB
由函数的图象可知函数是单调递增的,所以函数图象上任意一点处的导函数值都大于零,并且由图象可知,函数图象在处的切线斜率大于在处的切线斜率,所以;
记,,作直线AB,则直线AB的斜率,由函数图象,可知,
即.
故选:AB
4.(2)(3)
f′(1)=-3<0,则f(x)的图象在x=1处的切线斜率小于0;
又f(1)=3>0,所以f(x)的图象在x=1处位于x轴上方.
故答案为:(2)(3)
5.-2
根据导数的定义可得:
故答案为: 2
6.3x-y-4=0.
因为=3+Δx
所以切线的斜率k== (3+Δx)=3.
则切线方程为y-2=3(x-2),即3x-y-4=0.
巩固提升
1.A
故选:A.
2.C
由函数的图象可知,曲线在点A(1,f(1)),B(2,f(2)),C(3,f(3))处切线的斜率大小关系为kC>kB>kA,故f′(3)>f′(2)>f′(1).
3.D
由导数的几何意义,点处的切线斜率为,
因为时,,
所以,
所以在点处的切线斜率为,
故选:D.
4.B
因为在直线上,
所以,,
所以,
故选:B.
5.B
,
,
所以在点处切线的斜率为,
故切线的倾斜角为45°.
故选:B
6.C
上任意一点P(x0,y0)处的切线斜率为
=
= =<1,即k<1.
故选:C.
7.BC
函数在区间上的平均变化率为,由函数图象可得,在区间上,,即函数在区间上的平均变化率小于0;在区间,,上时,且相同,由图象可知函数在区间上的最大.
故选:BC
8.AC
,不存在只能说明曲线在该点处的切线斜率不存在;
当斜率不存在时,切线也可能存在,其切线方程为,故AC正确.
故选:AC.
9.AD
平均融化速度为,反映的是的图象与坐标轴交点连线的斜率,如图,观察可知,处瞬时速度(即切线的斜率)小于平均速度,,处瞬时速度及都小于0.
故选:AD
10.2
解析 f′(1)=
==2.
答案 2
11.③
①中函数在上的平均变化率为;
②中函数在上的平均变化率为;
③中函数在上的平均变化率为;
④中函数在上的平均变化率为.
观察可知,在上的平均变化率最大的是③.
故答案为:③
12.1
根据导数的定义知,
,
解得.
故答案为:1
13.①③④
①在时刻,为两图象的交点,即此时甲、乙两人血管中的药物浓度相同,故①正确;②甲、乙两人在时刻的切线的斜率不相等,即两人的不相同,所以甲、乙两人血管中药物浓度的瞬时变化率不相同,故②不正确;③根据平均变换率公式可知,甲、乙两人的平均变化率都是,故③正确;④在时间段,甲的平均变化率是,在时间段,甲的平均变化率是,显然不相等,故④正确.
故答案为:①③④
14.,其实际意义是:此时多生产1件产品,成本要增加1002.
设时,产量的改变量为,
,
则,即产量为500时的边际成本为1002,其实际意义是:此时多生产1件产品,成本要增加1002.
15.(1)
(2)
(1)
.
设为所求的点.
因为切线与直线平行,所以,
解得,所以,
即.
(2)
因为切线的倾斜角是135°,
所以其斜率为,即,解得.
所以,即.
16.
设,的导数为
由曲线在点A处的切线方程为,可得,,
解得,或,,
由点A在直线(其中,)上,
可得(,舍去),
则,
当且仅当即时,等号成立.
所以的最小值为.
平均变化率
1.(2021·江苏·高二课时练习)一物体的运动方程是,则t在内的平均速度为( )
A.0.41 B.4.1 C.0.3 D.3
2.(2021·辽宁·大连八中期中)函数,在[0,2]上的平均变化率分别记为,,则下列结论正确的是( )
A. B. C. D.,的大小无法确定
瞬时变化率(导数)
1.(2021·全国·高二同步练习)已知物体做自由落体的运动方程为,且无限趋近于0时,无限趋近于9.8m/s.那么关于9.8m/s正确的说法是( ).
A.物体在0~1s这一段时间内的速度
B.物体在这一段时间内的速度
C.物体在1s这一时刻的速度
D.物体从1s到这一段时间内的平均速度
2.(2020·全国·高二练习)某物体的运动路程s(单位:)与时间t(单位:)的关系可用函数s(t)=t3-2表示,则此物体在t0时的瞬时速度为27,则t0=________.
3.(2021·全国·高二课时练习)若函数在处可导,则的结果( ).
A.与,h均无关 B.仅与有关,而与h无关
C.仅与h有关,而与无关 D.与,h均有关
4.(原创)已知函数,求在处的导数.
5.(2021·河北·藁城新冀明中学高二阶段练习)已知,则___________.
导数的几何意义
1.(2021·全国·高二课时练习)已知的图象如图所示,则与的大小关系是( )
A.f′(xA)>f′(xB) B.f′(xA)<f′(xB)
C.f′(xA)=f′(xB) D.不能确定
2.(2021·陕西·武功县普集高级中学高二阶段练习(理))如图,函数的图象在点处的切线方程是,则( )
A.2 B.12 C.8 D.4
3.(2021·福建·泉州鲤城北大培文学校期中)(多选)已知函数的图象如图所示,是的导函数,则下列数值的排序正确的是( )
A. B.
C. D.
4.(2021·全国·高二课时练习)已知函数f(x)满足f(1)=3,f′(1)=-3,则下列关于f(x)的图象描述正确的是________.
(1)f(x)的图象在x=1处的切线斜率大于0;
(2)f(x)的图象在x=1处的切线斜率小于0;
(3)f(x)的图象在x=1处位于x轴上方;
(4)f(x)的图象在x=1处位于x轴下方.
5.(原创)抛物线y=x2+4在点(-1,5)处的切线的斜率为________.
6.(2021·全国·高二课时练习)求抛物线f(x)=x2-x在点(2,2)处的切线方程.
巩固提升
一、单选题
1.设函数y=f(x)=x2-1,当自变量x由1变为1.1时,函数的平均变化率为( )
A.2.1 B.1.1 C.2 D.0
2.函数f(x)的图象如图所示,则( )
A.f′(1)>f′(2)>f′(3) B.f′(2)>f′(1)>f′(3)
C.f′(3)>f′(2)>f′(1) D.f′(3)>f′(1)>f′(2)
3.设为可导函数,且,则曲线在点处的切线斜率为( )
A.2 B.-1 C.1 D.
4.函数在点处的切线方程是,则( )
A.2 B.3 C.4 D.5
5.已知抛物线上一点P,则在点P处的切线的倾斜角为( )
A.30° B.45°
C.135° D.165°
6.曲线y=x+上任意一点P处的切线斜率为k,则k的取值范围是( )
A.(-∞,-1) B.(-1,1)
C.(-∞,1) D.(1,+∞)
二、多选题
7.已知函数的图象如下图,则函数在区间上的平均变化率情况是( )
A.在区间上的平均变化率最小
B.在区间上的平均变化率大于0
C.在区间上的平均变化率比上的大
D.在区间上的平均变化率最大
8.下列说法正确的是( )
A.若不存在,则曲线在点处也可能有切线
B.若曲线在点处有切线,则必存在
C.若不存在,则曲线在点处的切线斜率不存在
D.若曲线在点处没有切线,则有可能存在
9.某堆雪在融化过程中,其体积V(单位:)与融化时间t(单位:h)近似满足函数关系:(H为常数),其图象如图所示,记此堆雪从融化开始到结束的平均融化速度为(单位:),,,,时刻的瞬时融化速度分别为,,,(单位:),那么下列各式正确的是( )
A. B. C. D.
三、填空题
10.设f(x)=2x+1,则f′(1)=________.
11.给出四个函数:①;②;③;④.其中在上的平均变化率最大的是______(填序号).
12.若函数在处的导数是8,则________.
13.为了评估某种治疗肺炎药物的疗效,现有关部门对该药物在人体血管中的药物浓度进行测量.设该药物在人体血管中药物浓度与时间的关系为,甲、乙两人服用该药物后,血管中药物浓度随时间变化的关系如下图所示.
给出下列四个结论:
① 在时刻,甲、乙两人血管中的药物浓度相同;
② 在时刻,甲、乙两人血管中药物浓度的瞬时变化率相同;
③ 在这个时间段内,甲、乙两人血管中药物浓度的平均变化率相同;
④ 在,两个时间段内,甲血管中药物浓度的平均变化率不相同.
其中所有正确结论的序号是_____.
四、解答题
14.已知某产品的总成本函数为,总成本函数在处导数称为在处的边际成本,用表示.求边际成本并说明它的实际意义.
15.在曲线E:上求出满足下列条件的点P的坐标.
(1)在点P处曲线E的切线平行于直线;
(2)在点P处曲线E的切线的倾斜角是135°.
16.若曲线在点A处的切线方程为,且点A在直线(其中,)上,求的最小值.
参考答案
平均变化率
1.B
,
故选:B
2.A
,,故.
故选:A.
瞬时变化率(导数)
1.C
由平均速度的概念,表示的是这一段时间内的平均速度,其极限值即,表示这一时刻的瞬时速度.
故选:C
2.3
解:由,得,
由题意得,解得.
因为,故.
故答案为:3
3.B
解:因为,
所以结果仅与有关,而与h无关,
故选:B.
4.6.
当自变量在处的改变量为时,平均变化率
.
化简,当无限接近于0时,无限接近于6,
因此
5.-8
解:令,
因为.
所以,
故答案为:.
导数的几何意义
1.B
由导数的几何意义可知,f′(xA),f′(xB)分别是切线在点A、B处切线的斜率,
由图象可知f′(xA)<f′(xB).
故选:B
2.A
解:根据题意,函数的图象在点处的切线方程是,
切点的横坐标为5,
则有(5),(5),
则(5)(5);
故选:A.
3.AB
由函数的图象可知函数是单调递增的,所以函数图象上任意一点处的导函数值都大于零,并且由图象可知,函数图象在处的切线斜率大于在处的切线斜率,所以;
记,,作直线AB,则直线AB的斜率,由函数图象,可知,
即.
故选:AB
4.(2)(3)
f′(1)=-3<0,则f(x)的图象在x=1处的切线斜率小于0;
又f(1)=3>0,所以f(x)的图象在x=1处位于x轴上方.
故答案为:(2)(3)
5.-2
根据导数的定义可得:
故答案为: 2
6.3x-y-4=0.
因为=3+Δx
所以切线的斜率k== (3+Δx)=3.
则切线方程为y-2=3(x-2),即3x-y-4=0.
巩固提升
1.A
故选:A.
2.C
由函数的图象可知,曲线在点A(1,f(1)),B(2,f(2)),C(3,f(3))处切线的斜率大小关系为kC>kB>kA,故f′(3)>f′(2)>f′(1).
3.D
由导数的几何意义,点处的切线斜率为,
因为时,,
所以,
所以在点处的切线斜率为,
故选:D.
4.B
因为在直线上,
所以,,
所以,
故选:B.
5.B
,
,
所以在点处切线的斜率为,
故切线的倾斜角为45°.
故选:B
6.C
上任意一点P(x0,y0)处的切线斜率为
=
= =<1,即k<1.
故选:C.
7.BC
函数在区间上的平均变化率为,由函数图象可得,在区间上,,即函数在区间上的平均变化率小于0;在区间,,上时,且相同,由图象可知函数在区间上的最大.
故选:BC
8.AC
,不存在只能说明曲线在该点处的切线斜率不存在;
当斜率不存在时,切线也可能存在,其切线方程为,故AC正确.
故选:AC.
9.AD
平均融化速度为,反映的是的图象与坐标轴交点连线的斜率,如图,观察可知,处瞬时速度(即切线的斜率)小于平均速度,,处瞬时速度及都小于0.
故选:AD
10.2
解析 f′(1)=
==2.
答案 2
11.③
①中函数在上的平均变化率为;
②中函数在上的平均变化率为;
③中函数在上的平均变化率为;
④中函数在上的平均变化率为.
观察可知,在上的平均变化率最大的是③.
故答案为:③
12.1
根据导数的定义知,
,
解得.
故答案为:1
13.①③④
①在时刻,为两图象的交点,即此时甲、乙两人血管中的药物浓度相同,故①正确;②甲、乙两人在时刻的切线的斜率不相等,即两人的不相同,所以甲、乙两人血管中药物浓度的瞬时变化率不相同,故②不正确;③根据平均变换率公式可知,甲、乙两人的平均变化率都是,故③正确;④在时间段,甲的平均变化率是,在时间段,甲的平均变化率是,显然不相等,故④正确.
故答案为:①③④
14.,其实际意义是:此时多生产1件产品,成本要增加1002.
设时,产量的改变量为,
,
则,即产量为500时的边际成本为1002,其实际意义是:此时多生产1件产品,成本要增加1002.
15.(1)
(2)
(1)
.
设为所求的点.
因为切线与直线平行,所以,
解得,所以,
即.
(2)
因为切线的倾斜角是135°,
所以其斜率为,即,解得.
所以,即.
16.
设,的导数为
由曲线在点A处的切线方程为,可得,,
解得,或,,
由点A在直线(其中,)上,
可得(,舍去),
则,
当且仅当即时,等号成立.
所以的最小值为.
