9.2.1-9.2.2总体取值规律的估计、总体百分位数的估计 同步练习 (含答案)
文档属性
| 名称 | 9.2.1-9.2.2总体取值规律的估计、总体百分位数的估计 同步练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览



文档简介
9.2 用样本估计总体
9.2.1 总体取值规律的估计
9.2.2 总体百分位数的估计
基础过关练
题组一 频率分布表
1.一个容量为100的样本,其数据的分组与各组的频数如下:
分组 [0,10) [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 12 13 24 15 16 13 7
则样本数据落在[10,40)上的频率为 ( )
A.0.13 B.0.39 C.0.52 D.0.64
2.一个容量为100的样本,将其数据按从小到大的顺序分为8组,如下表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
则第三组的频数和频率分别是 ( )
A.14和0.14 B.0.14和14 C.
题组二 频率分布直方图
3.(2021天津七校高三上期末联考)某学校组织部分学生参加体能测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18,则参加体能测试的学生人数是 ( )
A.45 B.48 C.50 D.60
4.将容量为n的样本中的数据分成6组,绘制频率分布直方图.若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n= .
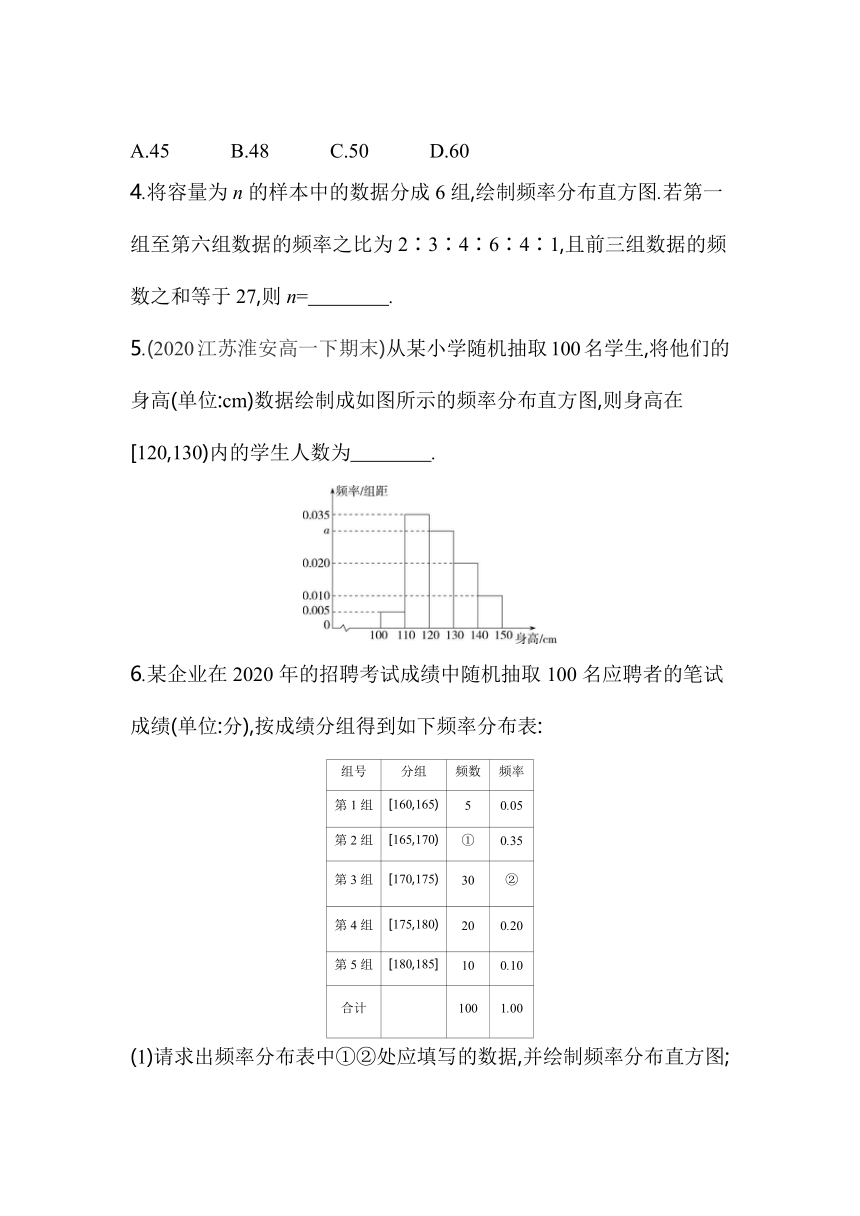
5.(2020江苏淮安高一下期末)从某小学随机抽取100名学生,将他们的身高(单位:cm)数据绘制成如图所示的频率分布直方图,则身高在[120,130)内的学生人数为 .
6.某企业在2020年的招聘考试成绩中随机抽取100名应聘者的笔试成绩(单位:分),按成绩分组得到如下频率分布表:
组号 分组 频数 频率
第1组 [160,165) 5 0.05
第2组 [165,170) ① 0.35
第3组 [170,175) 30 ②
第4组 [175,180) 20 0.20
第5组 [180,185] 10 0.10
合计 100 1.00
(1)请求出频率分布表中①②处应填写的数据,并绘制频率分布直方图;
(2)为了选拔出最优秀的应聘者,该企业决定在笔试成绩高的第3,4,5组中用比例分配的分层随机抽样方法抽取6名应聘者进入第二轮面试,求第3,4,5组每组各应抽取多少名应聘者进入第二轮面试.
题组三 条形图、扇形图、折线图
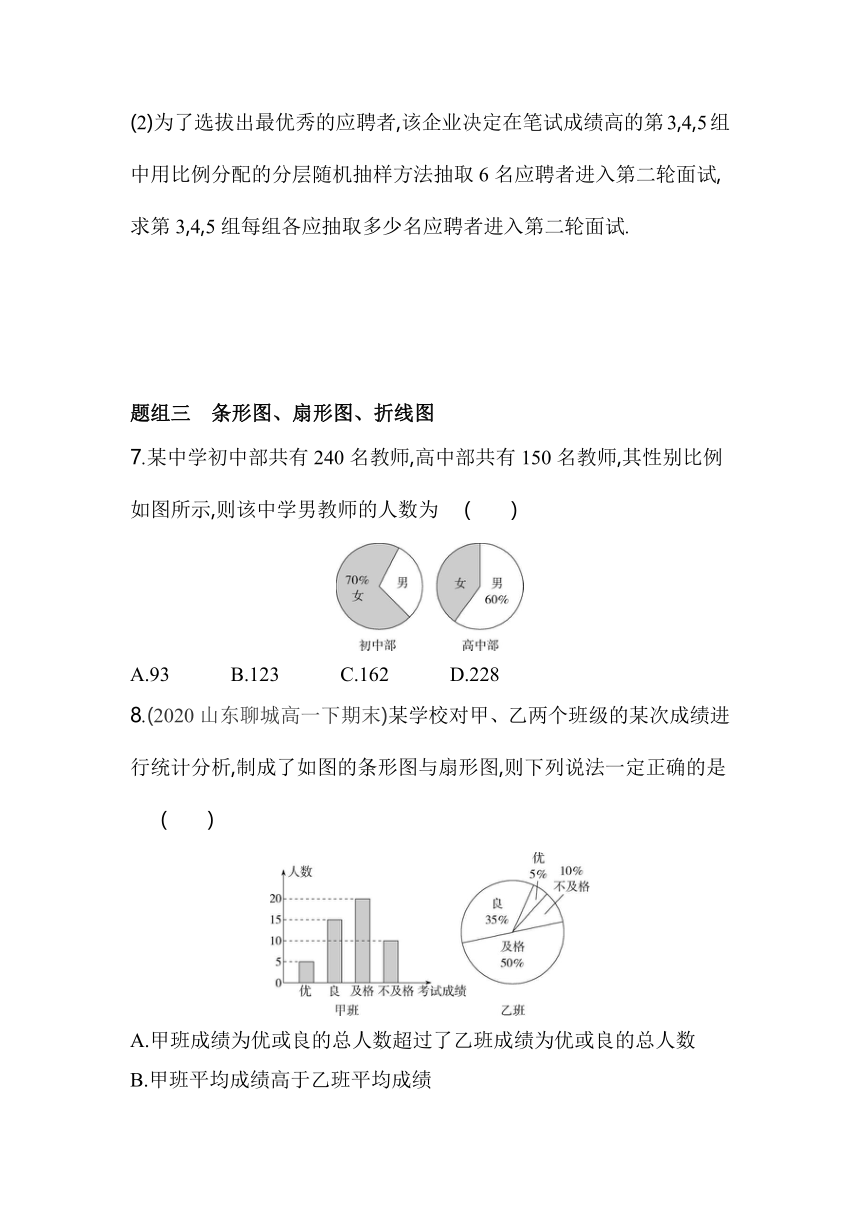
7.某中学初中部共有240名教师,高中部共有150名教师,其性别比例如图所示,则该中学男教师的人数为 ( )
A.93 B.123 C.162 D.228
8.(2020山东聊城高一下期末)某学校对甲、乙两个班级的某次成绩进行统计分析,制成了如图的条形图与扇形图,则下列说法一定正确的是 ( )
A.甲班成绩为优或良的总人数超过了乙班成绩为优或良的总人数
B.甲班平均成绩高于乙班平均成绩
C.甲班学生比乙班学生发挥稳定
D.甲班的不及格率高于乙班的不及格率
9.如图是根据某市3月1日至3月10日的最低气温(单位:℃)情况绘制的折线图,试根据折线图反映的信息完成下列问题.
(1)绘制该市3月1日到3月10日最低气温(单位:℃)的扇形图;
(2)绘制该市3月1日到3月10日最低气温(单位:℃)的条形图;
(3)比较以上折线图、扇形图、条形图的特点.
题组四 总体百分位数的估计
10.已知100个数据的第75百分位数是9.3,则下列说法正确的是 ( )
A.这100个数据中一定有75个数小于或等于9.3
B.把这100个数据按从小到大的顺序排列后,9.3是第75个数据
C.把这100个数据按从小到大的顺序排列后,9.3是第75个数据和第76个数据的平均数
D.把这100个数据按从小到大的顺序排列后,9.3是第74个数据和第75个数据的平均数
11.某棉纺厂为了了解一批棉花的质量,从中随机抽测了100根棉花的纤维长度(棉花的纤维长度是棉花质量的重要指标),所得数据都在区间[5,40](单位:mm)中,其频率分布直方图如图所示,由此估计棉花的纤维长度的样本数据的80%分位数是 ( )
A.28 B.28.5 C.29 D.29.5
12.从某珍珠公司生产的珍珠中任意抽取12颗,得到它们的质量(单位:g)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.
(1)分别求出这组数据的第25,75,95百分位数;
(2)请找出珍珠质量较小的前15%的珍珠质量;
(3)若用第25,50,95百分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品,依照这个样本的数据,给出该公司珍珠等级的划分标准.
能力提升练
题组一 统计图表的综合应用
1.()在抽查某产品尺寸的过程中,将其尺寸分成若干个小组,[a,b)是其中一组,抽查出的个体数在该组内的频率为m,在频率分布直方图中该组的高度为h,则|a-b|= ( )
A.hm B. D.h+m
2.(多选)(2020山东滨州高一下期末,)某市教育局和体育局对全市高三年级的学生身高进行抽样调查,随机抽取了100名学生身高,他们的身高都处在A,B,C,D,E五个层次内,根据抽样结果得到如下统计图,则下面叙述正确的是 ( )
A.样本中女生人数多于男生人数
B.样本中B层人数最多
C.样本中E层男生人数为6
D.样本中D层男生人数多于女生人数
3.()为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生的体重,将男生体重的数据整理后,画出了如图所示的频率分布直方图,已知图中从左到右前三个小组的频率之比为1∶2∶3,第二小组的频数为12,若全校男、女生比例为3∶2,则全校抽取的学生人数为 .
题组二 百分位数及其应用
4.(2020山东济南历城二中高一下5月学情检测,)已知甲、乙两组按顺序排列的数据:
甲组:27,28,37,m,40,50;
乙组:24,n,34,43,48,52.
若这两组数据的第30百分位数、第50百分位数分别对应相等,则等于 ( )
A.
5.()某班有n名学生,他们都参加了某次高三复习检测,第i个学生的某科成绩记为Xi(i=1,2,3,…,n),定义Pi=该科成绩不超过Xi的该班人数÷n为第i个学生的该科成绩的百分位.现对该班的甲、乙两名同学的该次检测成绩进行对比分析,若甲、乙两名同学的各科成绩的百分位如图所示,则以下分析不正确的是 ( )
A.甲同学的语文、数学、英语、综合的总分高于乙同学
B.甲同学的语文、数学、英语成绩都好于乙同学
C.甲同学的各科成绩都居该班上游(百分位大于66)
D.乙同学的语文分数不一定比数学分数高
6.()某大学艺术专业400名学生参加某次测评,根据男、女学生的人数比例,使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如图所示的频率分布直方图:
(1)估计400名学生中分数小于70的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学规定,把15%的学生划定为不及格,利用(2)中的数据,确定本次测试的及格分数线.
答案全解全析
基础过关练
1.C 样本数据落在[10,40)上的频数为13+24+15=52,故其频率为=0.52.
2.A 由题意知x=100-(10+13+14+15+13+12+9)=100-86=14,
故第三组的频数为14,
频率为=0.14.
3.D 根据题中频率分布直方图,得低于60分的频率是(0.005+0.01)×20=0.3,
所以参加体能测试的学生人数为=60.故选D.
4.答案 60
解析 设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x,x,则2x+3x+4x+6x+4x+x=1,解得x=0.05,所以前三组数据的频率分别是0.1,0.15,0.2,所以(0.1+0.15+0.2)×n=27,解得n=60.
5.答案 30
解析 由题图得(0.035+a+0.020+0.010+0.005)×10=1,解得a=0.03,
故身高在[120,130)内的学生人数为100×0.03×10=30.
6.解析 (1)由题意可知,第2组的频数为0.35×100=35,第3组的频率为=0.30,故①处应填35,②处应填0.30.
频率分布直方图如图所示.
(2)因为第3,4,5组共有60名应聘者,
所以利用比例分配的分层随机抽样的方法在60名应聘者中抽取6名应聘者的抽样比为,
故第3组应抽取30×=3名应聘者,
第4组应抽取20×=2名应聘者,第5组应抽取10×=1名应聘者,
所以第3,4,5组应抽取的应聘者人数分别为3,2,1.
7.C 由题意知初中部的男教师人数为240×(1-0.7)=72,
高中部的男教师人数为150×0.6=90.
因此该中学男教师的人数为72+90=162.故选C.
8.D 选项A中,因为乙班的总人数不确定,所以无法比较,故A不一定正确;选项B中,无法判断两个班平均成绩的高低,故B不一定正确;选项C中,一次成绩无法判断发挥是否稳定,故C不一定正确;选项D中,甲班的不及格率为×100%=20%,乙班的不及格率为10%,故甲班的不及格率高于乙班的不及格率,故D一定正确.故选D.
9.解析 该城市3月1日至3月10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气 温(℃) -3 -2 0 -1 1 2 0 -1 2 2
其中最低气温为-3 ℃的有1天,占10%;最低气温为-2 ℃的有1天,占10%;最低气温为-1 ℃的有2天,占20%;最低气温为0 ℃的有2天,占20%;最低气温为1 ℃的有1天,占10%;最低气温为2 ℃的有3天,占30%.
(1)绘制的扇形图如图所示.
(2)绘制的条形图如图所示.
(3)折线图能很好地描述数据随时间的变化趋势;扇形图更多用于描述各类数据占总体的比例;从条形图中可以更直观地看出事物的不同类型或分组数据的频数.
10.C 因为100×75%=75,为整数,所以第75个数据和第76个数据的平均数为第75百分位数.
11.C 棉花的纤维长度在25 mm(不含25 mm)以下的频率为(0.01+0.01+0.04+0.06)×5=0.6,在30 mm(不含30 mm)以下的频率为0.6+0.05×5=0.85,因此80%分位数一定位于[25,30)内,所以估计棉花的纤维长度的样本数据的80%分位数是25+5×=29.
12.解析 (1)将所有数据从小到大排列,得7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9,
因为12×25%=3,12×75%=9,12×95%=11.4,
所以第25百分位数是=8.15,
第75百分位数是=8.75,
第95百分位数是第12个数据9.9.
(2)因为12×15%=1.8,所以第15百分位数是第2个数据7.9,所以产品质量较小的前15%的珍珠有2个,它们的质量分别为7.8 g,7.9 g.
(3)由(1)可知,样本数据的第25百分位数是8.15,第50百分位数为8.5,第95百分位数是9.9,所以质量小于或等于8.15 g的珍珠为次品,质量大于8.15 g且小于或等于8.5 g的珍珠为合格品,质量大于8.5 g且小于或等于9.9 g的珍珠为优等品,质量大于9.9 g的珍珠为特优品.
能力提升练
1.B 根据频率分布直方图中小矩形的高为,可知=h,所以|a-b|=.故选B.
2.ABC 样本中女生人数为9+24+15+9+3=60,男生人数为100-60=40,故样本中女生人数多于男生人数,A正确;
样本中A层人数为9+40×10%=13,B层人数为24+40×30%=36,C层人数为15+40×25%=25,D层人数为9+40×20%=17,E层人数为3+40×(1-10%-30%-25%-20%)=9,故样本中B层人数最多,B正确;
样本中E层男生人数为40×(1-10%-30%-25%-20%)=6,C正确;
样本中D层男生人数为40×20%=8,女生人数为9,故样本中D层男生人数少于女生人数,D错误.
故选ABC.
3.答案 80
解析 由题图得,第四小组与第五小组的频率和为(0.037 5+0.012 5)×5=0.25.
因为从左到右前三个小组的频率之比为1∶2∶3,第二小组的频数为12,
所以前三个小组的频数和为36,所以抽取的男生人数为=48.
因为全校男、女生比例为3∶2,所以全校抽取的学生人数为48×=80.
4.B 因为30%×6=1.8,50%×6=3,所以甲组数据的第30百分位数为28,乙组数据的第30百分位数为n,甲组数据的第50百分位数为,乙组数据的第50百分位数为.
所以
所以.
5.A 由甲、乙两名同学的各科成绩的百分位图可知,在A中,甲同学的语文、数学、英语三科得分高于乙同学,综合得分低于乙同学,所以甲同学的语文、数学、英语、综合的总分不一定高于乙同学,故A错误;在B中,甲同学的语文、数学、英语成绩都好于乙同学,故B正确;在C中,甲同学的各科成绩百分位均超过66,所以甲同学的各科成绩都居该班的上游,故C正确;在D中,乙同学的语文分数不一定比数学分数高,故D正确.故选A.
6.解析 (1)根据题中频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.
所以估计400名学生中分数小于70的人数为400×0.4=160.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,分数在区间[40,50)内的人数为100-100×0.9-5=5.
所以估计总体中分数在区间[40,50)内的人数为400×=20.
(3)设样本中分数的第15百分位数为x,由(2)可知,分数小于50的频率为1-0.9=0.1,分数小于60的频率为0.1+0.1=0.2,所以x∈[50,60),则0.1+(x-50)×0.01=0.15,解得x=55,所以本次考试的及格分数线为55.
9.2.1 总体取值规律的估计
9.2.2 总体百分位数的估计
基础过关练
题组一 频率分布表
1.一个容量为100的样本,其数据的分组与各组的频数如下:
分组 [0,10) [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 12 13 24 15 16 13 7
则样本数据落在[10,40)上的频率为 ( )
A.0.13 B.0.39 C.0.52 D.0.64
2.一个容量为100的样本,将其数据按从小到大的顺序分为8组,如下表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
则第三组的频数和频率分别是 ( )
A.14和0.14 B.0.14和14 C.
题组二 频率分布直方图
3.(2021天津七校高三上期末联考)某学校组织部分学生参加体能测试,成绩的频率分布直方图如图,数据的分组依次是[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18,则参加体能测试的学生人数是 ( )
A.45 B.48 C.50 D.60
4.将容量为n的样本中的数据分成6组,绘制频率分布直方图.若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n= .
5.(2020江苏淮安高一下期末)从某小学随机抽取100名学生,将他们的身高(单位:cm)数据绘制成如图所示的频率分布直方图,则身高在[120,130)内的学生人数为 .
6.某企业在2020年的招聘考试成绩中随机抽取100名应聘者的笔试成绩(单位:分),按成绩分组得到如下频率分布表:
组号 分组 频数 频率
第1组 [160,165) 5 0.05
第2组 [165,170) ① 0.35
第3组 [170,175) 30 ②
第4组 [175,180) 20 0.20
第5组 [180,185] 10 0.10
合计 100 1.00
(1)请求出频率分布表中①②处应填写的数据,并绘制频率分布直方图;
(2)为了选拔出最优秀的应聘者,该企业决定在笔试成绩高的第3,4,5组中用比例分配的分层随机抽样方法抽取6名应聘者进入第二轮面试,求第3,4,5组每组各应抽取多少名应聘者进入第二轮面试.
题组三 条形图、扇形图、折线图
7.某中学初中部共有240名教师,高中部共有150名教师,其性别比例如图所示,则该中学男教师的人数为 ( )
A.93 B.123 C.162 D.228
8.(2020山东聊城高一下期末)某学校对甲、乙两个班级的某次成绩进行统计分析,制成了如图的条形图与扇形图,则下列说法一定正确的是 ( )
A.甲班成绩为优或良的总人数超过了乙班成绩为优或良的总人数
B.甲班平均成绩高于乙班平均成绩
C.甲班学生比乙班学生发挥稳定
D.甲班的不及格率高于乙班的不及格率
9.如图是根据某市3月1日至3月10日的最低气温(单位:℃)情况绘制的折线图,试根据折线图反映的信息完成下列问题.
(1)绘制该市3月1日到3月10日最低气温(单位:℃)的扇形图;
(2)绘制该市3月1日到3月10日最低气温(单位:℃)的条形图;
(3)比较以上折线图、扇形图、条形图的特点.
题组四 总体百分位数的估计
10.已知100个数据的第75百分位数是9.3,则下列说法正确的是 ( )
A.这100个数据中一定有75个数小于或等于9.3
B.把这100个数据按从小到大的顺序排列后,9.3是第75个数据
C.把这100个数据按从小到大的顺序排列后,9.3是第75个数据和第76个数据的平均数
D.把这100个数据按从小到大的顺序排列后,9.3是第74个数据和第75个数据的平均数
11.某棉纺厂为了了解一批棉花的质量,从中随机抽测了100根棉花的纤维长度(棉花的纤维长度是棉花质量的重要指标),所得数据都在区间[5,40](单位:mm)中,其频率分布直方图如图所示,由此估计棉花的纤维长度的样本数据的80%分位数是 ( )
A.28 B.28.5 C.29 D.29.5
12.从某珍珠公司生产的珍珠中任意抽取12颗,得到它们的质量(单位:g)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.
(1)分别求出这组数据的第25,75,95百分位数;
(2)请找出珍珠质量较小的前15%的珍珠质量;
(3)若用第25,50,95百分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品,依照这个样本的数据,给出该公司珍珠等级的划分标准.
能力提升练
题组一 统计图表的综合应用
1.()在抽查某产品尺寸的过程中,将其尺寸分成若干个小组,[a,b)是其中一组,抽查出的个体数在该组内的频率为m,在频率分布直方图中该组的高度为h,则|a-b|= ( )
A.hm B. D.h+m
2.(多选)(2020山东滨州高一下期末,)某市教育局和体育局对全市高三年级的学生身高进行抽样调查,随机抽取了100名学生身高,他们的身高都处在A,B,C,D,E五个层次内,根据抽样结果得到如下统计图,则下面叙述正确的是 ( )
A.样本中女生人数多于男生人数
B.样本中B层人数最多
C.样本中E层男生人数为6
D.样本中D层男生人数多于女生人数
3.()为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生的体重,将男生体重的数据整理后,画出了如图所示的频率分布直方图,已知图中从左到右前三个小组的频率之比为1∶2∶3,第二小组的频数为12,若全校男、女生比例为3∶2,则全校抽取的学生人数为 .
题组二 百分位数及其应用
4.(2020山东济南历城二中高一下5月学情检测,)已知甲、乙两组按顺序排列的数据:
甲组:27,28,37,m,40,50;
乙组:24,n,34,43,48,52.
若这两组数据的第30百分位数、第50百分位数分别对应相等,则等于 ( )
A.
5.()某班有n名学生,他们都参加了某次高三复习检测,第i个学生的某科成绩记为Xi(i=1,2,3,…,n),定义Pi=该科成绩不超过Xi的该班人数÷n为第i个学生的该科成绩的百分位.现对该班的甲、乙两名同学的该次检测成绩进行对比分析,若甲、乙两名同学的各科成绩的百分位如图所示,则以下分析不正确的是 ( )
A.甲同学的语文、数学、英语、综合的总分高于乙同学
B.甲同学的语文、数学、英语成绩都好于乙同学
C.甲同学的各科成绩都居该班上游(百分位大于66)
D.乙同学的语文分数不一定比数学分数高
6.()某大学艺术专业400名学生参加某次测评,根据男、女学生的人数比例,使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如图所示的频率分布直方图:
(1)估计400名学生中分数小于70的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学规定,把15%的学生划定为不及格,利用(2)中的数据,确定本次测试的及格分数线.
答案全解全析
基础过关练
1.C 样本数据落在[10,40)上的频数为13+24+15=52,故其频率为=0.52.
2.A 由题意知x=100-(10+13+14+15+13+12+9)=100-86=14,
故第三组的频数为14,
频率为=0.14.
3.D 根据题中频率分布直方图,得低于60分的频率是(0.005+0.01)×20=0.3,
所以参加体能测试的学生人数为=60.故选D.
4.答案 60
解析 设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x,x,则2x+3x+4x+6x+4x+x=1,解得x=0.05,所以前三组数据的频率分别是0.1,0.15,0.2,所以(0.1+0.15+0.2)×n=27,解得n=60.
5.答案 30
解析 由题图得(0.035+a+0.020+0.010+0.005)×10=1,解得a=0.03,
故身高在[120,130)内的学生人数为100×0.03×10=30.
6.解析 (1)由题意可知,第2组的频数为0.35×100=35,第3组的频率为=0.30,故①处应填35,②处应填0.30.
频率分布直方图如图所示.
(2)因为第3,4,5组共有60名应聘者,
所以利用比例分配的分层随机抽样的方法在60名应聘者中抽取6名应聘者的抽样比为,
故第3组应抽取30×=3名应聘者,
第4组应抽取20×=2名应聘者,第5组应抽取10×=1名应聘者,
所以第3,4,5组应抽取的应聘者人数分别为3,2,1.
7.C 由题意知初中部的男教师人数为240×(1-0.7)=72,
高中部的男教师人数为150×0.6=90.
因此该中学男教师的人数为72+90=162.故选C.
8.D 选项A中,因为乙班的总人数不确定,所以无法比较,故A不一定正确;选项B中,无法判断两个班平均成绩的高低,故B不一定正确;选项C中,一次成绩无法判断发挥是否稳定,故C不一定正确;选项D中,甲班的不及格率为×100%=20%,乙班的不及格率为10%,故甲班的不及格率高于乙班的不及格率,故D一定正确.故选D.
9.解析 该城市3月1日至3月10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气 温(℃) -3 -2 0 -1 1 2 0 -1 2 2
其中最低气温为-3 ℃的有1天,占10%;最低气温为-2 ℃的有1天,占10%;最低气温为-1 ℃的有2天,占20%;最低气温为0 ℃的有2天,占20%;最低气温为1 ℃的有1天,占10%;最低气温为2 ℃的有3天,占30%.
(1)绘制的扇形图如图所示.
(2)绘制的条形图如图所示.
(3)折线图能很好地描述数据随时间的变化趋势;扇形图更多用于描述各类数据占总体的比例;从条形图中可以更直观地看出事物的不同类型或分组数据的频数.
10.C 因为100×75%=75,为整数,所以第75个数据和第76个数据的平均数为第75百分位数.
11.C 棉花的纤维长度在25 mm(不含25 mm)以下的频率为(0.01+0.01+0.04+0.06)×5=0.6,在30 mm(不含30 mm)以下的频率为0.6+0.05×5=0.85,因此80%分位数一定位于[25,30)内,所以估计棉花的纤维长度的样本数据的80%分位数是25+5×=29.
12.解析 (1)将所有数据从小到大排列,得7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9,
因为12×25%=3,12×75%=9,12×95%=11.4,
所以第25百分位数是=8.15,
第75百分位数是=8.75,
第95百分位数是第12个数据9.9.
(2)因为12×15%=1.8,所以第15百分位数是第2个数据7.9,所以产品质量较小的前15%的珍珠有2个,它们的质量分别为7.8 g,7.9 g.
(3)由(1)可知,样本数据的第25百分位数是8.15,第50百分位数为8.5,第95百分位数是9.9,所以质量小于或等于8.15 g的珍珠为次品,质量大于8.15 g且小于或等于8.5 g的珍珠为合格品,质量大于8.5 g且小于或等于9.9 g的珍珠为优等品,质量大于9.9 g的珍珠为特优品.
能力提升练
1.B 根据频率分布直方图中小矩形的高为,可知=h,所以|a-b|=.故选B.
2.ABC 样本中女生人数为9+24+15+9+3=60,男生人数为100-60=40,故样本中女生人数多于男生人数,A正确;
样本中A层人数为9+40×10%=13,B层人数为24+40×30%=36,C层人数为15+40×25%=25,D层人数为9+40×20%=17,E层人数为3+40×(1-10%-30%-25%-20%)=9,故样本中B层人数最多,B正确;
样本中E层男生人数为40×(1-10%-30%-25%-20%)=6,C正确;
样本中D层男生人数为40×20%=8,女生人数为9,故样本中D层男生人数少于女生人数,D错误.
故选ABC.
3.答案 80
解析 由题图得,第四小组与第五小组的频率和为(0.037 5+0.012 5)×5=0.25.
因为从左到右前三个小组的频率之比为1∶2∶3,第二小组的频数为12,
所以前三个小组的频数和为36,所以抽取的男生人数为=48.
因为全校男、女生比例为3∶2,所以全校抽取的学生人数为48×=80.
4.B 因为30%×6=1.8,50%×6=3,所以甲组数据的第30百分位数为28,乙组数据的第30百分位数为n,甲组数据的第50百分位数为,乙组数据的第50百分位数为.
所以
所以.
5.A 由甲、乙两名同学的各科成绩的百分位图可知,在A中,甲同学的语文、数学、英语三科得分高于乙同学,综合得分低于乙同学,所以甲同学的语文、数学、英语、综合的总分不一定高于乙同学,故A错误;在B中,甲同学的语文、数学、英语成绩都好于乙同学,故B正确;在C中,甲同学的各科成绩百分位均超过66,所以甲同学的各科成绩都居该班的上游,故C正确;在D中,乙同学的语文分数不一定比数学分数高,故D正确.故选A.
6.解析 (1)根据题中频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.
所以估计400名学生中分数小于70的人数为400×0.4=160.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,分数在区间[40,50)内的人数为100-100×0.9-5=5.
所以估计总体中分数在区间[40,50)内的人数为400×=20.
(3)设样本中分数的第15百分位数为x,由(2)可知,分数小于50的频率为1-0.9=0.1,分数小于60的频率为0.1+0.1=0.2,所以x∈[50,60),则0.1+(x-50)×0.01=0.15,解得x=55,所以本次考试的及格分数线为55.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
