2021—2022学年北师大版九年级数学下册1.4解直角三角形同步测试(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版九年级数学下册1.4解直角三角形同步测试(Word版含答案) | 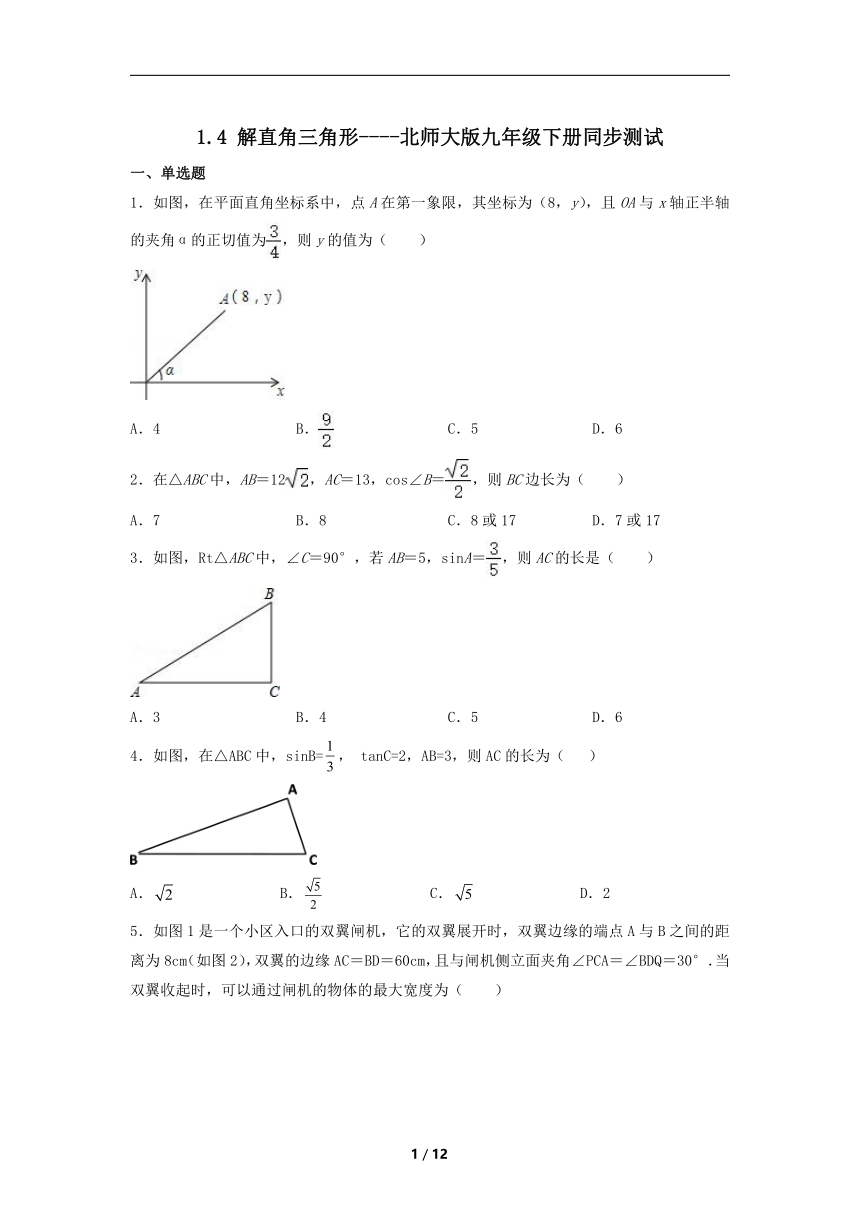 | |
| 格式 | docx | ||
| 文件大小 | 501.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 23:21:21 | ||
图片预览





文档简介
1.4 解直角三角形----北师大版九年级下册同步测试
一、单选题
1.如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为,则y的值为( )
A.4 B. C.5 D.6
2.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为( )
A.7 B.8 C.8或17 D.7或17
3.如图,Rt△ABC中,∠C=90°,若AB=5,sinA=,则AC的长是( )
A.3 B.4 C.5 D.6
4.如图,在△ABC中,sinB=, tanC=2,AB=3,则AC的长为( )
A. B. C. D.2
5.如图1是一个小区入口的双翼闸机,它的双翼展开时,双翼边缘的端点A与B之间的距离为8cm(如图2),双翼的边缘AC=BD=60cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.608 B.608 C.64 D.68
6.如图,两条宽度都为1的纸条,交叉重叠放在一起,它们的夹角为锐角,它们重叠部分(阴影部分)的面积是1.5,那么的值为()
A. B. C. D.
7.构造几何图形解决代数问题是“数形结合思想”的重要应用,小康在计算 时,构造出如图所示的图形:在Rt ACD中, , ,延长 到 , ,连接 ,得 .根据此图可求得 的结果( )
A. B. C. D.
二、填空题
8.如图,在边长为1的小正方形网格中,点A、B、C均在格点上,则tan∠B的值为 .
9.如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离为________海里.
10.下图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯次点B到点C上升的高度h是_____m.
11.如图,AC⊥BC,AD=a,BD=b,∠A=α,∠B=β,则AC等于 _______.
三、解答题
12.如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.
13.在中,,a,b,c分别为,,的对边,根据下列条件求出直角三角形的其他元素(边长精确到0.01):
(1);
(2);
(3);
(4).
14.在Rt中,,,,求,的度数.
15.如图,某防洪大坝的横截面是梯形,迎水坡的坡角为30°,坝顶宽度为2米,坝高为4米,背水坡的坡度.
(1)求该堤坝的横截面积(结果保留根号);
(2)为更好应对可能来临的汛情,防洪指挥部决定加固堤坝,要求坝高不变,坝顶宽度增加1米,背水坡的坡度改为,求加固后的堤坝的横截面积(结果保留根号).
四、综合题
16.如图1在平面直角坐标系中,O是坐标原点, ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2 ),点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线l与x轴交于点F,与射线DC交于点G.
(1)求∠DCB的度数;
(2)连接OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△OEF',记直线EF'与射线DC的交点为H.
①如图2,当点G在点H的左侧时,求证:△DEG∽△DHE;
②若△EHG的面积为3 ,求点F的坐标.
17.如图所示,已知△ABC中,AB=6,BC=5,sinB=,求△ABC的面积.
18.如图,平行四边形ABCD在平面直角坐标系中,AD=6.若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB;
(1)求sin∠ABC的值;
(2)若E为x轴上的点,且S△AOE=,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由.
19.已知:如图,在Rt△ABC中,∠C=90°,AC=.点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).
20.如图1,在平面内有射线Ox和一点A,连接OA,若OA=1.5,∠AOx=30°,则可用(1.5,30°)表示点A的位置,如图2,在平面内有一点B(2,60°),以O为坐标原点,以Ox为x轴建立平面直角坐标系,求点B在平面直角坐标系xOy内的坐标.
答案
1.B
2.A
3.C
4.C
5.B
6.A
7.C
8.
9.
10.(1,2)
11.
12.解:∵∠C=90°,∠ADC="45°,AC=5,
∴ AC=CD=5, AD=
∵ SinB= ,
∴ AB=AC/(SinB)=13,
∵∠C=90°, CD=5,
∴ BC=12,
∴ BD=7,
过B 作BE⊥AD交AD的延长线于E ,
∵∠BDE=∠ADC=45°,
∴ BE=DE=7÷ = ,
∴ AE=AD+DE= ,
∴tan = .
13.(1);(2);(3);(4).
【解析】解:(1)∵∠A=10°,
∴∠B=90° ∠A=80°,
∵sin∠A=,
∴c=≈46.07,
由勾股定理可求出:b≈45.37;
(2)∵∠B=33°,
∴∠A=90° ∠B=57°,
∵sin∠B=,
∴c=≈9.18,
∴由勾股定理可求出:a≈7.70;
(3)∵a=5,c=13,
∴由勾股定理可求出:b=12,
∵sin∠A==,
∴∠A≈,
∴∠B=90° =;
(4)∵c=,b=,
∴由勾股定理可知:a=8,
∵sin∠A==,
∴∠A≈,
∴∠B≈.
14.,
【解析】Rt △ABC 中, ∠C=90° ,
∵
∴
∴∠B=90゜ -∠A=60゜
15.(1);
(2)
【解析】(1)过点D作DF⊥BC于点F,如图,
则DF=AE=4,EF=AD=2
∵,且AE=4
∴BE=4
∵
∴
∴
∴
∴
(2)
如图,过点G作GQ⊥BC于点Q,则四边形GQEA是矩形,
∴GQ=AE=4,QE=AG=1
∵背水坡度为
∴
∴
∴ ,GD=GA+AD=1+2=3
∴
16.(1)解:在 中,
∵ ,
∴ ,
∵四边形ABCD是平行四边形,
∴ ;
(2)解:①证明:∵ , ,且E是AD的中点,
∴ , , ,
∴ 是等边三角形,则 ,
根据轴对称的性质知: ,故 ,即 ,
∴ ,
∵ ,
∴ ,
又∵ ,
∴ ;
②过点E作 直线CD于点M,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,即 ,
当点H在点G的右侧时,设 , ,
∴ ,
解得: , (舍),
∴点F的坐标为 ;
当点H在点G的左侧时,设 , ,
∴ ,
解得: , (舍),
∵ ,
∴ ,
∵ ,
∴点F的坐标为 ;
综上所述:点F的坐标有两个,分别是 , .
17.解:如图,作AD⊥BC的延长线于D;
由题意得:AB=6,sinB=,则AD=AB sinB=6×=2;
又BC=5,则S△ABC=×BC×AD=×5×2=5;
故△ABC的面积为5.
18.解:(1)解方程:x2﹣7x+12=0
解得x1=3,x2=4(1分)
∵OA>OB
∴OA=4,OB=3(2分)
由勾股定理得出:
∴AB=5(3分)
∴在Rt△OAB中,sin∠ABC==(4分)
(2)①∵S△AOE=
∴OA OE=
∴OE=(5分)
∴点E的坐标为(﹣,0)或(,0)(6分)
②△AOE与△DAO相似,理由如下:
∵=,
∴
∵∠AOE=∠DAO=90°(7分)
∴△AOE∽△DAO.(8分)
19.解:在Rt△ADC中,
∵sin∠ADC=,
∴AD===2.
∴BD=2AD=4,
∵tan∠ADC=,DC===1,
∴BC=BD+DC=5.
在Rt△ABC中,AB==2,
∴△ABC的周长=AB+BC+AC=2+5+.
20.解:作BC⊥OX于点C,
∵OB=2,∠BOX=60°,
∴OC=OB×cos60°=1,BC=OB×sin60°=,
∴点B在平面直角坐标系xOy内的坐标为:(1,).
1 / 3
一、单选题
1.如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为,则y的值为( )
A.4 B. C.5 D.6
2.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为( )
A.7 B.8 C.8或17 D.7或17
3.如图,Rt△ABC中,∠C=90°,若AB=5,sinA=,则AC的长是( )
A.3 B.4 C.5 D.6
4.如图,在△ABC中,sinB=, tanC=2,AB=3,则AC的长为( )
A. B. C. D.2
5.如图1是一个小区入口的双翼闸机,它的双翼展开时,双翼边缘的端点A与B之间的距离为8cm(如图2),双翼的边缘AC=BD=60cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.608 B.608 C.64 D.68
6.如图,两条宽度都为1的纸条,交叉重叠放在一起,它们的夹角为锐角,它们重叠部分(阴影部分)的面积是1.5,那么的值为()
A. B. C. D.
7.构造几何图形解决代数问题是“数形结合思想”的重要应用,小康在计算 时,构造出如图所示的图形:在Rt ACD中, , ,延长 到 , ,连接 ,得 .根据此图可求得 的结果( )
A. B. C. D.
二、填空题
8.如图,在边长为1的小正方形网格中,点A、B、C均在格点上,则tan∠B的值为 .
9.如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离为________海里.
10.下图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯次点B到点C上升的高度h是_____m.
11.如图,AC⊥BC,AD=a,BD=b,∠A=α,∠B=β,则AC等于 _______.
三、解答题
12.如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.
13.在中,,a,b,c分别为,,的对边,根据下列条件求出直角三角形的其他元素(边长精确到0.01):
(1);
(2);
(3);
(4).
14.在Rt中,,,,求,的度数.
15.如图,某防洪大坝的横截面是梯形,迎水坡的坡角为30°,坝顶宽度为2米,坝高为4米,背水坡的坡度.
(1)求该堤坝的横截面积(结果保留根号);
(2)为更好应对可能来临的汛情,防洪指挥部决定加固堤坝,要求坝高不变,坝顶宽度增加1米,背水坡的坡度改为,求加固后的堤坝的横截面积(结果保留根号).
四、综合题
16.如图1在平面直角坐标系中,O是坐标原点, ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2 ),点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线l与x轴交于点F,与射线DC交于点G.
(1)求∠DCB的度数;
(2)连接OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△OEF',记直线EF'与射线DC的交点为H.
①如图2,当点G在点H的左侧时,求证:△DEG∽△DHE;
②若△EHG的面积为3 ,求点F的坐标.
17.如图所示,已知△ABC中,AB=6,BC=5,sinB=,求△ABC的面积.
18.如图,平行四边形ABCD在平面直角坐标系中,AD=6.若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB;
(1)求sin∠ABC的值;
(2)若E为x轴上的点,且S△AOE=,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由.
19.已知:如图,在Rt△ABC中,∠C=90°,AC=.点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).
20.如图1,在平面内有射线Ox和一点A,连接OA,若OA=1.5,∠AOx=30°,则可用(1.5,30°)表示点A的位置,如图2,在平面内有一点B(2,60°),以O为坐标原点,以Ox为x轴建立平面直角坐标系,求点B在平面直角坐标系xOy内的坐标.
答案
1.B
2.A
3.C
4.C
5.B
6.A
7.C
8.
9.
10.(1,2)
11.
12.解:∵∠C=90°,∠ADC="45°,AC=5,
∴ AC=CD=5, AD=
∵ SinB= ,
∴ AB=AC/(SinB)=13,
∵∠C=90°, CD=5,
∴ BC=12,
∴ BD=7,
过B 作BE⊥AD交AD的延长线于E ,
∵∠BDE=∠ADC=45°,
∴ BE=DE=7÷ = ,
∴ AE=AD+DE= ,
∴tan = .
13.(1);(2);(3);(4).
【解析】解:(1)∵∠A=10°,
∴∠B=90° ∠A=80°,
∵sin∠A=,
∴c=≈46.07,
由勾股定理可求出:b≈45.37;
(2)∵∠B=33°,
∴∠A=90° ∠B=57°,
∵sin∠B=,
∴c=≈9.18,
∴由勾股定理可求出:a≈7.70;
(3)∵a=5,c=13,
∴由勾股定理可求出:b=12,
∵sin∠A==,
∴∠A≈,
∴∠B=90° =;
(4)∵c=,b=,
∴由勾股定理可知:a=8,
∵sin∠A==,
∴∠A≈,
∴∠B≈.
14.,
【解析】Rt △ABC 中, ∠C=90° ,
∵
∴
∴∠B=90゜ -∠A=60゜
15.(1);
(2)
【解析】(1)过点D作DF⊥BC于点F,如图,
则DF=AE=4,EF=AD=2
∵,且AE=4
∴BE=4
∵
∴
∴
∴
∴
(2)
如图,过点G作GQ⊥BC于点Q,则四边形GQEA是矩形,
∴GQ=AE=4,QE=AG=1
∵背水坡度为
∴
∴
∴ ,GD=GA+AD=1+2=3
∴
16.(1)解:在 中,
∵ ,
∴ ,
∵四边形ABCD是平行四边形,
∴ ;
(2)解:①证明:∵ , ,且E是AD的中点,
∴ , , ,
∴ 是等边三角形,则 ,
根据轴对称的性质知: ,故 ,即 ,
∴ ,
∵ ,
∴ ,
又∵ ,
∴ ;
②过点E作 直线CD于点M,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,即 ,
当点H在点G的右侧时,设 , ,
∴ ,
解得: , (舍),
∴点F的坐标为 ;
当点H在点G的左侧时,设 , ,
∴ ,
解得: , (舍),
∵ ,
∴ ,
∵ ,
∴点F的坐标为 ;
综上所述:点F的坐标有两个,分别是 , .
17.解:如图,作AD⊥BC的延长线于D;
由题意得:AB=6,sinB=,则AD=AB sinB=6×=2;
又BC=5,则S△ABC=×BC×AD=×5×2=5;
故△ABC的面积为5.
18.解:(1)解方程:x2﹣7x+12=0
解得x1=3,x2=4(1分)
∵OA>OB
∴OA=4,OB=3(2分)
由勾股定理得出:
∴AB=5(3分)
∴在Rt△OAB中,sin∠ABC==(4分)
(2)①∵S△AOE=
∴OA OE=
∴OE=(5分)
∴点E的坐标为(﹣,0)或(,0)(6分)
②△AOE与△DAO相似,理由如下:
∵=,
∴
∵∠AOE=∠DAO=90°(7分)
∴△AOE∽△DAO.(8分)
19.解:在Rt△ADC中,
∵sin∠ADC=,
∴AD===2.
∴BD=2AD=4,
∵tan∠ADC=,DC===1,
∴BC=BD+DC=5.
在Rt△ABC中,AB==2,
∴△ABC的周长=AB+BC+AC=2+5+.
20.解:作BC⊥OX于点C,
∵OB=2,∠BOX=60°,
∴OC=OB×cos60°=1,BC=OB×sin60°=,
∴点B在平面直角坐标系xOy内的坐标为:(1,).
1 / 3
