2021-2022学年北师大版八年级数学下册2.1不等关系 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册2.1不等关系 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 387.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 14:22:43 | ||
图片预览





文档简介
(共18张PPT)
课题:2.1不等关系
大小
高度
长度
速度
情景导入
在我们的生活中,既有相等关系又有不等关系.
前面我们用等式(包括方程)研究相等关系.
要研究不等关系也需要专门的数学工具——不等式.
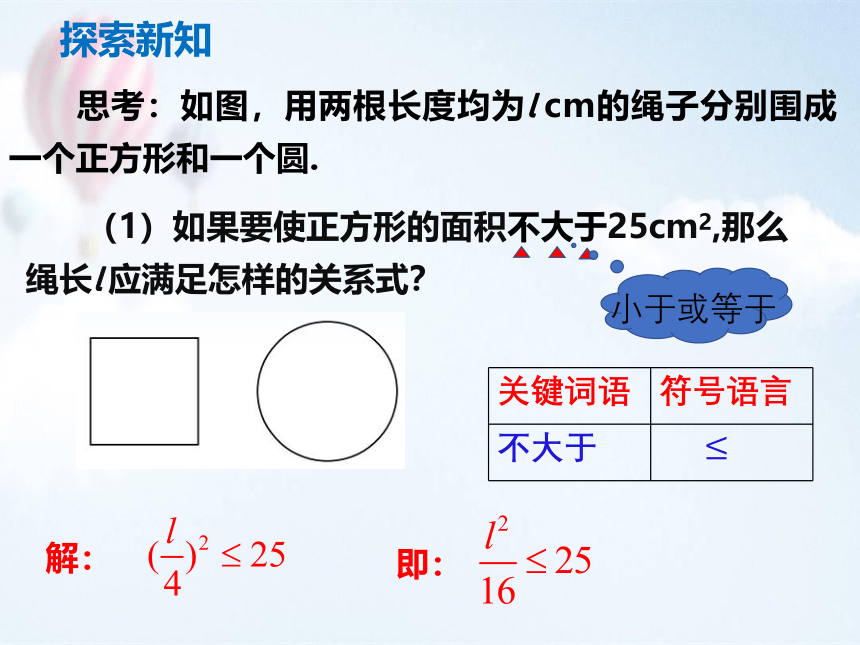
思考:如图,用两根长度均为l cm的绳子分别围成一个正方形和一个圆.
(1)如果要使正方形的面积不大于25cm2,那么绳长l 应满足怎样的关系式?
关键词语 符号语言
不大于
探索新知
解:
即:
小于或等于
(2)如果要使圆的面积不小于100cm2,那么绳长l 应满足怎样的关系式?
关键词语 符号语言
不小于
解:
即:
大于或等于
(3)当 l= 8 时,正方形和圆的面积哪个大? l = 12 呢?改变l的取值,你能得到什么猜想?
解:
当l= 8 时,
∵4< 5.1
∴当l = 8 时,圆的面积大.
当l = 12 时,
∵9< 11.5
∴当l = 12 时,还是圆的面积大.
做一做:
(1)铁路部门对旅客随身携带的行李有如下规定:每件行李的长、宽、高 三边之和不得超过160 cm.设行李的长、宽、高分别为a cm,b cm,c cm, 请你列出行李的长、宽、高满足的关系式.
关键词语 符号语言
不得超过
解:行李的长款
小于或等于
做一做:
(2)通过测量一棵树的树围(树干的周长)可以计算出它的树龄. 通常规定以树干离地面1.5 m的地方为测量部位. 某树栽种时的树围为6 cm,以后10年内每年增加约3 cm,设经过x年后这棵树的树围超过30 cm,请你列出x 满足的关系式.
解:x 满足的关系式为:
6+3x>30
关键词语 符号语言
超过
大于
议一议:观察由上述问题得到的关系式:
它们有什么共同特点?
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式.
特别地:a+2≠3也是不等式
归纳总结
练习1.下列各式是不等式的有______________.
(1)8<9; (2)a+b=0;
(3)a2+1>0; (4)3x-1≤x;
(5)x-y≠1; (6)3-x=0;
(7)4-2x; (8)x2+y2≥0.
初试牛刀
(1)(3)(4)(5)(8)
解题关键:判断式子中是否有不等号.
练习2:用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a,b都长;
(3)x与17的和比它的5倍小;
(4)两数的平方和不小于这两数积的2倍.
解:(1)a≥0;(2)c>a,c>b;(3)x+17<5x;(4)x2+y2≥2xy.
解题关键:先抓住不等关系的关键词,再选准不等号.
第一类----明显的不等关系
关键 词语 大于 超过比…大 小于 低于比…小 不大于不超过至多 不小于 不低于 至少 大于或
小于
不等号
归纳总结
特别要注意“不”
>0
<0
≥0
≤0
第二类----隐含的不等关系
关键 词语 正数 负数 非负数 非正数
不等号
练习1:用适当的符号表示下列关系:
(1)X的3倍与8的和比x的5倍大;
(2)是非负数;
(3)地球上海洋面积大于陆地面积;
(4)老师的年龄比你年龄的2倍还大;
(5)铅球的质量比篮球的质量大.
巩固练习
练习2.用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表所示:
(1)现配制这种饮料10Kg,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(Kg)应满足的不等式;
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(Kg)应满足的另一个不等式吗?
甲 乙
维生素C(单位/Kg) 600 100
原料价格(元/Kg) 8 4
原料
列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
归纳总结
练习3、设计不同的实际背景来表示下列不等式:
(1)
(2)
思维拓展
课堂小结
本节课你有哪些收获?
1、不等式的概念
2、列不等式的方法
3、建模思想
感谢聆听
课题:2.1不等关系
大小
高度
长度
速度
情景导入
在我们的生活中,既有相等关系又有不等关系.
前面我们用等式(包括方程)研究相等关系.
要研究不等关系也需要专门的数学工具——不等式.
思考:如图,用两根长度均为l cm的绳子分别围成一个正方形和一个圆.
(1)如果要使正方形的面积不大于25cm2,那么绳长l 应满足怎样的关系式?
关键词语 符号语言
不大于
探索新知
解:
即:
小于或等于
(2)如果要使圆的面积不小于100cm2,那么绳长l 应满足怎样的关系式?
关键词语 符号语言
不小于
解:
即:
大于或等于
(3)当 l= 8 时,正方形和圆的面积哪个大? l = 12 呢?改变l的取值,你能得到什么猜想?
解:
当l= 8 时,
∵4< 5.1
∴当l = 8 时,圆的面积大.
当l = 12 时,
∵9< 11.5
∴当l = 12 时,还是圆的面积大.
做一做:
(1)铁路部门对旅客随身携带的行李有如下规定:每件行李的长、宽、高 三边之和不得超过160 cm.设行李的长、宽、高分别为a cm,b cm,c cm, 请你列出行李的长、宽、高满足的关系式.
关键词语 符号语言
不得超过
解:行李的长款
小于或等于
做一做:
(2)通过测量一棵树的树围(树干的周长)可以计算出它的树龄. 通常规定以树干离地面1.5 m的地方为测量部位. 某树栽种时的树围为6 cm,以后10年内每年增加约3 cm,设经过x年后这棵树的树围超过30 cm,请你列出x 满足的关系式.
解:x 满足的关系式为:
6+3x>30
关键词语 符号语言
超过
大于
议一议:观察由上述问题得到的关系式:
它们有什么共同特点?
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式.
特别地:a+2≠3也是不等式
归纳总结
练习1.下列各式是不等式的有______________.
(1)8<9; (2)a+b=0;
(3)a2+1>0; (4)3x-1≤x;
(5)x-y≠1; (6)3-x=0;
(7)4-2x; (8)x2+y2≥0.
初试牛刀
(1)(3)(4)(5)(8)
解题关键:判断式子中是否有不等号.
练习2:用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a,b都长;
(3)x与17的和比它的5倍小;
(4)两数的平方和不小于这两数积的2倍.
解:(1)a≥0;(2)c>a,c>b;(3)x+17<5x;(4)x2+y2≥2xy.
解题关键:先抓住不等关系的关键词,再选准不等号.
第一类----明显的不等关系
关键 词语 大于 超过比…大 小于 低于比…小 不大于不超过至多 不小于 不低于 至少 大于或
小于
不等号
归纳总结
特别要注意“不”
>0
<0
≥0
≤0
第二类----隐含的不等关系
关键 词语 正数 负数 非负数 非正数
不等号
练习1:用适当的符号表示下列关系:
(1)X的3倍与8的和比x的5倍大;
(2)是非负数;
(3)地球上海洋面积大于陆地面积;
(4)老师的年龄比你年龄的2倍还大;
(5)铅球的质量比篮球的质量大.
巩固练习
练习2.用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表所示:
(1)现配制这种饮料10Kg,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(Kg)应满足的不等式;
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(Kg)应满足的另一个不等式吗?
甲 乙
维生素C(单位/Kg) 600 100
原料价格(元/Kg) 8 4
原料
列不等式的一般步骤:
(1)分析题意,找出问题中的各种量;
(2)弄清各种量之间的数量关系;
(3)用代数式表示各种量;
(4)用适当的不等号将具有不等关系的量连接起来.
归纳总结
练习3、设计不同的实际背景来表示下列不等式:
(1)
(2)
思维拓展
课堂小结
本节课你有哪些收获?
1、不等式的概念
2、列不等式的方法
3、建模思想
感谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
