2021-2022学年北师大版数学八年级下册3.2图形的旋转 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级下册3.2图形的旋转 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 14:34:00 | ||
图片预览





文档简介
(共17张PPT)
课题:图形的旋转(一)
情境引入
思考:观察下面生活中的现象,你能说出它们共同的特点吗?
风力发电
钟表
游乐场中的摩天轮
知识要点
旋转中心
这个定点称为旋转中心,
转动的角称为旋转角.
旋转方向
旋转角
注意:旋转不改变图形的形状和大小.
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
旋转的定义
转动的方向分为顺时针与逆时针.
典型例题
例1:下列运动属于旋转的是( )
A.温度计中,液柱的上升或下降
B.把一个图形沿某直线对折
C.直升机升空的过程
D.钟表钟摆的摆动
D
典型例题
例2:如图所示,△ABC是直角三角形,延长AB到D,
使BD=BC,在BC上取BE=AB,连接DE.△ABC
旋转后能与△EBD重合,那么:旋转中心是______;
旋转的方向是________;旋转的角度是________;
AC的对应边是________;
∠A的对应角是________;
点C的对应点是________.
点B
90°
ED
∠BED
点D
顺时针
归纳总结
旋转中心
旋转角
旋转方向
必须明确
确定图形的旋转时
温馨提示:①旋转的范围是“平面内”,其中“旋转中心,
旋转方向,旋转角度”称之为旋转的三要素;②旋转变换
同样属于全等变换.
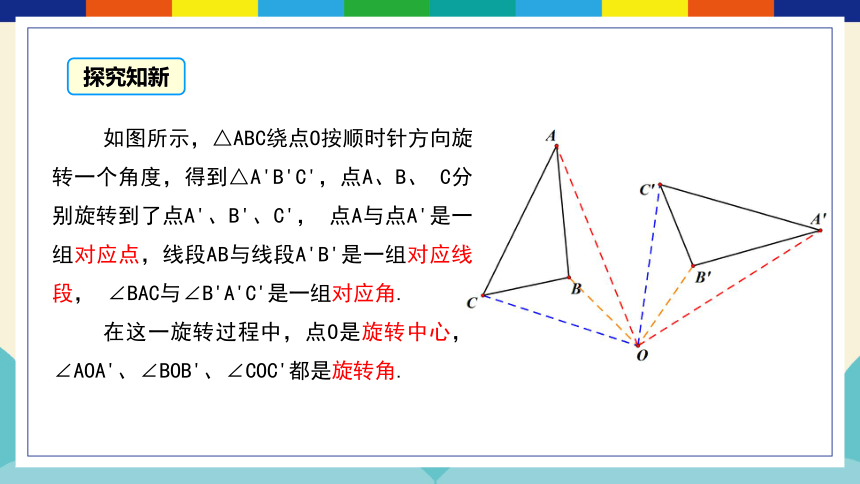
如图所示,△ABC绕点O按顺时针方向旋转一个角度,得到△A'B'C',点A、B、 C分别旋转到了点A'、B'、C', 点A与点A'是一组对应点,线段AB与线段A'B'是一组对应线段, ∠BAC与∠B'A'C'是一组对应角.
在这一旋转过程中,点O是旋转中心, ∠AOA'、∠BOB'、∠COC'都是旋转角.
探究知新
典型例题
例3:如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
C
A.30° B.45°
C.90° D.135°
解析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.
知识要点
旋转的性质
1、旋转不改变图形的大小和形状.
2、对应线段相等,对应角相等.
3、对应点到旋转中心的距离相等.
4、任意一组对应点与旋转中心的连线所成的角都等于旋转角.
①△ABC≌△A'B'C' ②AO=A'O,BO=B'O,CO=C'O
③∠AOA'=∠BOB'=∠COC'
典型例题
例4:如图所示,(1)~(4)的四个三角形中,哪个
不能由△ABC经过平移或旋转得到?
答:图(2)不能.
典型例题
例5:如图,你能绕点O旋转,使得线段AB与线段CD重合吗?为什么?
不重合,因为OA≠OC,OB≠OD
当堂练习
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
当堂练习
2. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
B
当堂练习
3. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将Rt△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30° B.60°
C.45° D.90°
B
60°
当堂练习
变式: 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,将Rt△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则线段B'B的长度为( )
A.3 B.
C.6 D.
D
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
课堂小结
同学们再见
课题:图形的旋转(一)
情境引入
思考:观察下面生活中的现象,你能说出它们共同的特点吗?
风力发电
钟表
游乐场中的摩天轮
知识要点
旋转中心
这个定点称为旋转中心,
转动的角称为旋转角.
旋转方向
旋转角
注意:旋转不改变图形的形状和大小.
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
旋转的定义
转动的方向分为顺时针与逆时针.
典型例题
例1:下列运动属于旋转的是( )
A.温度计中,液柱的上升或下降
B.把一个图形沿某直线对折
C.直升机升空的过程
D.钟表钟摆的摆动
D
典型例题
例2:如图所示,△ABC是直角三角形,延长AB到D,
使BD=BC,在BC上取BE=AB,连接DE.△ABC
旋转后能与△EBD重合,那么:旋转中心是______;
旋转的方向是________;旋转的角度是________;
AC的对应边是________;
∠A的对应角是________;
点C的对应点是________.
点B
90°
ED
∠BED
点D
顺时针
归纳总结
旋转中心
旋转角
旋转方向
必须明确
确定图形的旋转时
温馨提示:①旋转的范围是“平面内”,其中“旋转中心,
旋转方向,旋转角度”称之为旋转的三要素;②旋转变换
同样属于全等变换.
如图所示,△ABC绕点O按顺时针方向旋转一个角度,得到△A'B'C',点A、B、 C分别旋转到了点A'、B'、C', 点A与点A'是一组对应点,线段AB与线段A'B'是一组对应线段, ∠BAC与∠B'A'C'是一组对应角.
在这一旋转过程中,点O是旋转中心, ∠AOA'、∠BOB'、∠COC'都是旋转角.
探究知新
典型例题
例3:如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
C
A.30° B.45°
C.90° D.135°
解析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.
知识要点
旋转的性质
1、旋转不改变图形的大小和形状.
2、对应线段相等,对应角相等.
3、对应点到旋转中心的距离相等.
4、任意一组对应点与旋转中心的连线所成的角都等于旋转角.
①△ABC≌△A'B'C' ②AO=A'O,BO=B'O,CO=C'O
③∠AOA'=∠BOB'=∠COC'
典型例题
例4:如图所示,(1)~(4)的四个三角形中,哪个
不能由△ABC经过平移或旋转得到?
答:图(2)不能.
典型例题
例5:如图,你能绕点O旋转,使得线段AB与线段CD重合吗?为什么?
不重合,因为OA≠OC,OB≠OD
当堂练习
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
当堂练习
2. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
B
当堂练习
3. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将Rt△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30° B.60°
C.45° D.90°
B
60°
当堂练习
变式: 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,将Rt△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则线段B'B的长度为( )
A.3 B.
C.6 D.
D
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
课堂小结
同学们再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
