2021-2022学年湖南省株洲市茶陵县九年级(上)期末数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年湖南省株洲市茶陵县九年级(上)期末数学试卷(word解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 00:00:00 | ||
图片预览

文档简介
2021-2022学年湖南省株洲市茶陵县九年级第一学期期末数学试卷
一、选择题(每小题有且只有一个正确答案,本题共10小题,每小题4分,共40分)
1.化简的正确结果是( )
A.±2 B.﹣2 C.2 D.4
2.下面四个图形,是中心对称图形的是( )
A. B. C. D.
3.如图所示在△ABC中,AB边上的高线画法正确的是( )
A. B.
C. D.
4.下列运算正确的是( )
A.(3m2)2=6m4 B.m2 m3=m5
C.3m﹣m=2 D.(m+1)2=m2+1
5.在2021年3月8日当天,由贾玲导演并主演的电影《你好,李焕英》,收获约46120000元票房,将46120000用科学记数法表示是( )
A.4612×104 B.4.612×108 C.46.12×106 D.4.612×107
6.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,11,13,15.关于这组数据,冉冉得出如下结果,其中错误的是( )
A.众数是11 B.平均数是12 C.方差是 D.中位数是13
7.实数a在数轴上的对应点的位置如图所示.若实数b满足﹣a<b<a,则b的值可以是( )
A.﹣3 B.﹣2 C.﹣1 D.2
8.直线y=x+a不经过第二象限,则关于x的方程ax2+2x+1=0实数解的个数是( )
A.0个 B.1个 C.2个 D.1个或2个
9.如图,在△ABC中,∠C=90°,点D在斜边AB上,且AD=CD,则下列结论中错误的结论是( )
A.∠DCB=∠B B.BC=BD
C.AD=BD D.∠ACD=∠BDC
10.如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2021次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2021次移动中,跳棋停留的顶点是( )
A.A B.B C.E D.G
二、填空题(本题共8小题,每小题4分,共32分)
11.使有意义的x的取值范围是 .
12.因式分解:3y2﹣12= .
13.若方程x2+kx﹣2=0的一个根是﹣2,则k的值是 .
14.如图:将一副直角三角板(∠A=30°,∠E=45°)按如图所示的位置摆放,使AB∥EF,则∠DOC的度数是 .
15.抗击“新冠肺炎”线上学习期间,某校为了解学校1000名九年级学生一周体育锻炼时间的情况,随机调查了50名九年级学生,并绘制成如图所示的条形统计图.根据图中数据,估计该校1000名九年级学生一周的体育锻炼时间不少于7小时的人数是 人.
16.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为 .
17.如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上.过点P分别作x轴、y轴的垂线,垂足分别为A、B,取线段OB的中点C,连接PC并延长交x轴于点D.则△APD的面积为 .
18.抛物线y=ax2+3ax+b的一部分图象如图,设该抛物线与x轴的交点为A(﹣5,0)和B,与y轴的交点为C,若△ACO∽△CBO,则∠CAB的正切值为 .
三、解答题(本题共7小题,共78分)
19.计算:.
20.先化简,再求值:,其中x=.
21.在平行四边形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BC=5,求CD的长.
22.驾驶员在驾驶车辆行驶过程中都会产生视觉盲区,如图,△ABC、△FED区域分别为该驾驶员在驾车行驶过程中的左右盲区,铅直高度AC、FD分别为盲高,BC、ED分别为盲宽,驾驶员视线PB与地面所在水平线BE的夹角∠PBE=45°,视线PE与地面BE的夹角∠PEB=30°,点A,F为视线与车窗底端的交点,AF∥BE,AC⊥BE,FD⊥BE.若点A到点B的距离AB=2m.
(1)求盲高AC;
(2)求右盲区△FED面积.
23.据新浪网调查,2019年全国网民最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图1所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题.
(1)求出图1中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年的年平均增长率约为多少?(≈3.16)
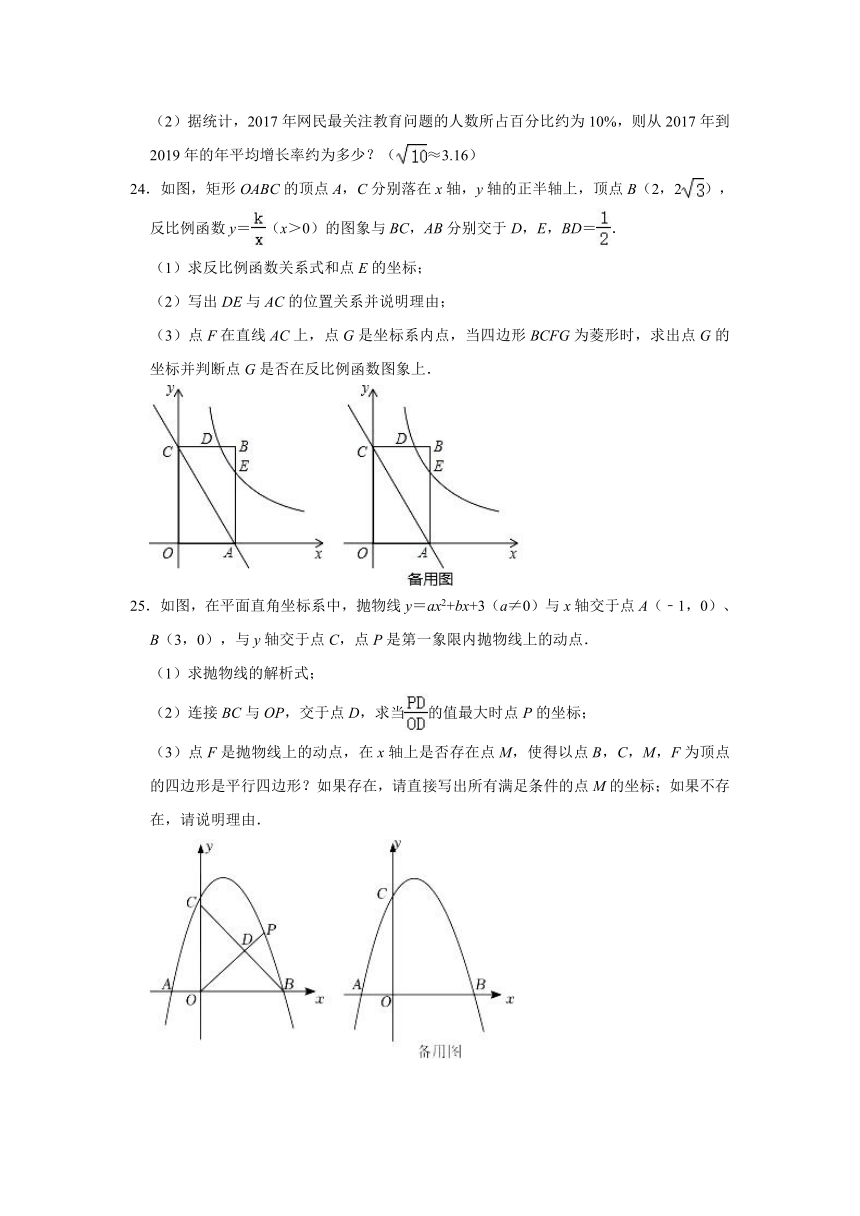
24.如图,矩形OABC的顶点A,C分别落在x轴,y轴的正半轴上,顶点B(2,2),反比例函数y=(x>0)的图象与BC,AB分别交于D,E,BD=.
(1)求反比例函数关系式和点E的坐标;
(2)写出DE与AC的位置关系并说明理由;
(3)点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点P是第一象限内抛物线上的动点.
(1)求抛物线的解析式;
(2)连接BC与OP,交于点D,求当的值最大时点P的坐标;
(3)点F是抛物线上的动点,在x轴上是否存在点M,使得以点B,C,M,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点M的坐标;如果不存在,请说明理由.
参考答案
一、选择题(每小题有且只有一个正确答案,本题共10小题,每小题4分,共40分)
1.化简的正确结果是( )
A.±2 B.﹣2 C.2 D.4
【分析】根据二次根式的基本性质进行化简求解即可.
解:=2.
故选:C.
2.下面四个图形,是中心对称图形的是( )
A. B. C. D.
【分析】根据中心对称图形的定义,结合选项所给图形进行判断即可.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
解:A.不是中心对称图形,故本选项不符合题意;
B.不是中心对称图形,故本选项不符合题意;
C.不是中心对称图形,故本选项不符合题意;
D.是中心对称图形,故本选项符合题意.
故选:D.
3.如图所示在△ABC中,AB边上的高线画法正确的是( )
A. B.
C. D.
【分析】直接利用高线的概念得出答案.
解:在△ABC中,AB边上的高线画法正确的是B,
故选:B.
4.下列运算正确的是( )
A.(3m2)2=6m4 B.m2 m3=m5
C.3m﹣m=2 D.(m+1)2=m2+1
【分析】根据完全平方公式、整式的乘法运算、乘方运算以及减法运算法则即可求出答案.
解:A、原式=9m4,故A不符合题意.
B、原式=m5,故B符合题意.
C、原式=2m,故C不符合题意.
D、原式=m2+2m+1,故D不符合题意.
故选:B.
5.在2021年3月8日当天,由贾玲导演并主演的电影《你好,李焕英》,收获约46120000元票房,将46120000用科学记数法表示是( )
A.4612×104 B.4.612×108 C.46.12×106 D.4.612×107
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,且n比原来的整数位数少1,据此判断即可.
解:46120000=4.612×107.
故选:D.
6.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,11,13,15.关于这组数据,冉冉得出如下结果,其中错误的是( )
A.众数是11 B.平均数是12 C.方差是 D.中位数是13
【分析】根据平均数、众数、中位数、方差的计算方法分别计算这组数据的平均数、众数、中位数、方差,最后做出选择.
解:数据11,10,11,13,11,13,15中,11出现的次数最多是3次,因此众数是11,于是A选项不符合题意;
将这7个数据从小到大排列后,处在中间位置的一个数是11,因此中位数是11,于是D符合题意;
=(11+10+11+13+11+13+15)÷7=12,即平均数是12,于是选项B不符合题意;
S2=[(10﹣12)2+(11﹣12)2×3+(13﹣12)2×2+(15﹣12)2]=,因此方差为,于是选项C不符合题意;
故选:D.
7.实数a在数轴上的对应点的位置如图所示.若实数b满足﹣a<b<a,则b的值可以是( )
A.﹣3 B.﹣2 C.﹣1 D.2
【分析】根据点b在数轴上的位置可求.
解:将﹣a,b在数轴上表示出来如下:
∵﹣a<b<a.
∴b在﹣a和a之间.
选项中只有﹣1符合条件.
故选:C.
8.直线y=x+a不经过第二象限,则关于x的方程ax2+2x+1=0实数解的个数是( )
A.0个 B.1个 C.2个 D.1个或2个
【分析】利用一次函数的性质得到a≤0,再判断Δ=22﹣4a>0,从而得到方程根的情况.
解:∵直线y=x+a不经过第二象限,
∴a≤0,
当a=0时,关于x的方程ax2+2x+1=0是一元一次方程,解为x=﹣,
当a<0时,关于x的方程ax2+2x+1=0是一元二次方程,
∵Δ=22﹣4a>0,
∴方程有两个不相等的实数根.
故选:D.
9.如图,在△ABC中,∠C=90°,点D在斜边AB上,且AD=CD,则下列结论中错误的结论是( )
A.∠DCB=∠B B.BC=BD
C.AD=BD D.∠ACD=∠BDC
【分析】根据等腰三角形的性质,可得∠A=∠ACD,再利用等角的余角相等得∠B=∠DCB,从而得DC=DB,然后可得AD=BD,然后逐一判断即可.
解:∵AD=CD,
∴∠A=∠ACD,
∵∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠BCD=90°,
∴∠B=∠BCD,
∴A正确,故A不符合题意;
∵∠BDC≠∠BCD,
∴BD≠BC,
∴B错误,故B符合题意;
∵∠B=∠BCD,
∴BD=DC,
∴AD=BD,
∴C正确,故C不符合题意;
∵∠BDC=∠A+∠ACD,∠A=∠ACD,
∴∠ACD=∠BDC,
∴D正确,故D不符合题意;
故选:B.
10.如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2021次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2021次移动中,跳棋停留的顶点是( )
A.A B.B C.E D.G
【分析】将棋子转圈的字母按顺序依次排成一列,然后找到循环的规律,即可解决.
解:根据题意可得,前7次移动后跳棋停留的顶点分别是B、D、G、D、B、A、A,
所以跳棋停留的顶点7次一个循环,
2021÷7=288……5,
故第2021次移动后停留的点是B,
故选:D.
二、填空题(本题共8小题,每小题4分,共32分)
11.使有意义的x的取值范围是 x≥1 .
【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.
解:∵有意义,
∴x﹣1≥0,解得x≥1.
故答案为:x≥1.
12.因式分解:3y2﹣12= 3(y+2)(y﹣2) .
【分析】先提取公因式3,再对余下的多项式利用平方差公式继续分解.
解:3y2﹣12,
=3(y2﹣4),
=3(y+2)(y﹣2).
13.若方程x2+kx﹣2=0的一个根是﹣2,则k的值是 1 .
【分析】将x=﹣2代入题目中的方程,即可求得k的值,本题得以解决.
解:∵一元二次方程x2+kx﹣2=0的一个根是﹣2,
∴(﹣2)2+k×(﹣2)﹣2=0,
解得,k=1,
故答案为:1.
14.如图:将一副直角三角板(∠A=30°,∠E=45°)按如图所示的位置摆放,使AB∥EF,则∠DOC的度数是 75° .
【分析】在Rt△DEF中由两角互余得∠F=45°,根据直线AB∥EF得∠A=∠ACF,再由三角形的内角和定理和邻补角的知识求出∠DOC=75°.
解:如图所示:
∵∠D=90°,
∴∠E+∠F=90°,
又∵∠E=45°,
∴∠F=45°,
又∵AB∥EF,
∴∠A=∠ACF,
又∵∠A=30°,
∴∠ACF=30°,
又∵∠ACF+∠F+∠1=180°,
∴∠1=105°,
又∵∠1+∠DOC=180°,
∴∠DOC=75°,
故答案为75°.
15.抗击“新冠肺炎”线上学习期间,某校为了解学校1000名九年级学生一周体育锻炼时间的情况,随机调查了50名九年级学生,并绘制成如图所示的条形统计图.根据图中数据,估计该校1000名九年级学生一周的体育锻炼时间不少于7小时的人数是 400 人.
【分析】用该校的总人数乘以一周的体育锻炼时间不少于7小时的人数所占的百分比即可.
解:根据题意得:1000×=400(人),
答:该校1000名九年级学生一周的体育锻炼时间不少于7小时的人数是400人;
故答案为:400.
16.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为 .
【分析】在△ABC中,由锐角三角函数求得AB,再由勾股定理求得BC,最后在△BCD中由锐角三角函数求得BD.
解:∵∠C=90°,AC=4,cosA=,
∴AB=5,
∴BC===3,
∵∠DBC=∠A.
∴cos∠DBC=cos∠A==,
∴BD=3×=,
故答案为:.
17.如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上.过点P分别作x轴、y轴的垂线,垂足分别为A、B,取线段OB的中点C,连接PC并延长交x轴于点D.则△APD的面积为 6 .
【分析】根据已知条件证得△PBC≌△DOC,再根据反比例函数系数k的几何意义即可得到结论.
解:∵PB⊥y轴,PA⊥x轴,
∴S矩形APBO=|k|=6,
在△PBC与△DOC中,
,
∴△PBC≌△DOC,
∴S△APD=S矩形APBO=6.
故答案为:6.
18.抛物线y=ax2+3ax+b的一部分图象如图,设该抛物线与x轴的交点为A(﹣5,0)和B,与y轴的交点为C,若△ACO∽△CBO,则∠CAB的正切值为 .
【分析】由对称轴可得点B的坐标,由于点C在y轴上,所以可写出点C的坐标,进而再由相似三角形对应边成比例求解点C的坐标,即可得出结论.
解:设B点的坐标为(x,0),
∵抛物线对称轴为直线x=﹣=﹣=﹣,
∴点B的横坐标为,
∴x=2,即B(2,0),
∴AO=5 BO=2.
∵△ACO∽△CBO,
∴,
∴,
∴OC=.
∴∠CAB的正切值=.
故答案为:.
三、解答题(本题共7小题,共78分)
19.计算:.
【分析】直接利用特殊角的三角函数值以及零指数幂的性质、绝对值的性质分别化简,进而计算得出答案.
解:原式=
=1﹣1+5
=5.
20.先化简,再求值:,其中x=.
【分析】根据分式的混合运算法则把原式化简,把x的值代入计算即可.
解:原式=(﹣)÷
=×
=,
当x=﹣1时,原式==.
21.在平行四边形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BC=5,求CD的长.
【分析】(1)由平行四边形的性质得到AB∥CD,AB=CD,推出四边形DFBE是平行四边形,根据矩形的判定定理即可得到结论;
(2)由矩形的性质得DE=BF,由角平分线的定义得到∠DCF=∠BCF,由平行线的性质得到∠DCF=∠CFB,证出BF=BC=5,进而得到结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形DFBE是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形DFBE是矩形;
(2)解:由(1)得:四边形DFBE是矩形,
∴DE=BF,
∵CF平分∠DCB,
∴∠DCF=∠BCF,
∵AB∥CD,
∴∠DCF=∠CFB,
∴∠BCF=∠CFB,
∴BF=BC=5,
∴DE=BF=5,
∴CD=DE+CE=5+3=8.
22.驾驶员在驾驶车辆行驶过程中都会产生视觉盲区,如图,△ABC、△FED区域分别为该驾驶员在驾车行驶过程中的左右盲区,铅直高度AC、FD分别为盲高,BC、ED分别为盲宽,驾驶员视线PB与地面所在水平线BE的夹角∠PBE=45°,视线PE与地面BE的夹角∠PEB=30°,点A,F为视线与车窗底端的交点,AF∥BE,AC⊥BE,FD⊥BE.若点A到点B的距离AB=2m.
(1)求盲高AC;
(2)求右盲区△FED面积.
【分析】(1)根据AC=AB sin45°求解即可;
(2)解直角三角形求出DE,DF,可得结论.
解:(1)∵FD⊥EB,AC⊥EB,
∴DF∥AC,
∵AF∥EB,
∴四边形ACDF是平行四边形,
∵∠ACD=90°,
∴四边形ACDF是矩形,
∴DF=AC,
在Rt△ACB中,∠ACB=90°,
∴AC=AB sin45°==(m),
(2)∵DF=AC=(m),
在Rt△DEF中,∠FDE=90°,
∴tan∠E=,
∴DE===(m).
所以右盲区△FED面积=××=(m2).
23.据新浪网调查,2019年全国网民最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图1所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题.
(1)求出图1中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年的年平均增长率约为多少?(≈3.16)
【分析】(1)求出反腐占的百分比,得到x的值;再由环保人数除以所占的百分比得到总人数,然后求出教育与反腐及其他的人数,补全条形统计图即可;
(2)设2017年到2019年的年平均增长率为x,则2018年网民最关注教育问题的人数所占百分比约为10%(1+x),2019年网民最关注教育问题的人数所占百分比约为10%(1+x)2,由2019年网民最关注教育问题的人数所占百分比约为25%,再由2019年网民最关注教育问题的人数所占百分比不变列出方程,解方程即可.
解:(1)关注“反腐”类问题的网民所占百分比为:1﹣15%﹣30%﹣25%﹣10%=20%,
∴x=20,
关注该五类热点问题网民的总人数为:140÷10%=1400(人),
则关注教育问题网民的人数为:1400×25%=350(人),
关注反腐问题网民的人数为:1400×20%=280(人),
关注其它问题网民的人数为:1400×15%=210(人),
补全条形统计图如下:
(2)设2017年到2019年的年平均增长率为x,
由题意得:10%(1+x)2=25%,
解得:x1≈0.58=58%,x2≈﹣2.58(不合题意,舍去).
答:从2017年到2019年的年平均增长率约为58%.
24.如图,矩形OABC的顶点A,C分别落在x轴,y轴的正半轴上,顶点B(2,2),反比例函数y=(x>0)的图象与BC,AB分别交于D,E,BD=.
(1)求反比例函数关系式和点E的坐标;
(2)写出DE与AC的位置关系并说明理由;
(3)点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.
【分析】(1)求出D(,2),再用待定系数法即可求解;
(2)证明=,即可求解;
(3)①当点F在点C的下方时,求出FH=1,CH=,求出点F(1,),则点G(3,),即可求解;②当点F在点C的上方时,同理可解.
解:(1)∵B(2,2),则BC=2,
而BD=,
∴CD=2﹣=,故点D(,2),
将点D的坐标代入反比例函数表达式得:2=,解得k=3,
故反比例函数表达式为y=,
当x=2时,y=,故点E(2,);
(2)由(1)知,D(,2),点E(2,),点B(2,2),
则BD=,BE=,
故==,===,
∴DE∥AC;
(3)①当点F在点C的下方时,
当点G在点F的右方时,如下图,
过点F作FH⊥y轴于点H,
∵四边形BCFG为菱形,则BC=CF=FG=BG=2,
在Rt△OAC中,OA=BC=2,OC=AB=2,
则tan∠OCA===,故∠OCA=30°,
则FH=FC=1,CH=CF cos∠OCA=2×=,
故点F(1,),则点G(3,),
当x=3时,y==,故点G在反比例函数图象上;
②当点F在点C的上方时,
同理可得,点G(1,3),
同理可得,点G在反比例函数图象上;
综上,点G的坐标为(3,)或(1,3)都在反比例函数图象上.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点P是第一象限内抛物线上的动点.
(1)求抛物线的解析式;
(2)连接BC与OP,交于点D,求当的值最大时点P的坐标;
(3)点F是抛物线上的动点,在x轴上是否存在点M,使得以点B,C,M,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点M的坐标;如果不存在,请说明理由.
【分析】(1)利用待定系数法可求解析式;
(2)过点P作PG⊥x轴,交BC与G,先求出直线BC的解析式,设点P(p,﹣p2+2p+3),则点G坐标为(p,﹣p+3),可求PG的长,由平行线分线段成比例可得=,利用二次函数的性质可求解;
(3)存在.由题意C(0,3),分图中三种情形,利用平行四边形的性质以及平移变换的性质求解即可.
解:(1)∵抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),
∴,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)如图1,过点P作PG⊥x轴,交BC于G,
∵抛物线的解析式为y=﹣x2+2x+3与y轴交于点C,
∴点C(0,3),
∴直线BC解析式为y=﹣x+3,
设点P(p,﹣p2+2p+3),则点G坐标为(p,﹣p+3),
∴PG=﹣p2+2p+3﹣(﹣p+3)=﹣p2+3p,
∵PG∥OC,
∴===﹣(p﹣)2+,
∴当p=时,的值有最大值,
∴点P(,);
(3)存在,满足条件的点M的坐标为(1,0)或(5,0)或(,0)或(﹣,0).理由如下:
设点M的坐标为(m,0),
当BC是平行四边形BCMF的边时,如图1,
点C(0,3)平移到点B(3,0),先向下平移3个单位,再向右平移3个单位,
则点M1(m,0),平移到F1(m+3,﹣3),
令﹣x2+2x+3=﹣3,可得m+3=1±;
∴m=﹣2±;
∴M1(﹣,0),M2(,0).
当BC是平行四边形BCFM的边时,如图2,
∴点B(3,0)平移到点C(0,3),先向上平移3个单位,再向左平移3个单位,
则点M1(m,0),平移到F1(m﹣3,3),
令﹣x2+2x+3=3,可得m﹣3=0或2;
∴m=3(舍)或m=5;
∴M3(5,0).
当BC是平行四边形BMCF的对角线时,BM∥CF,且BM=CF,
由上可知,点F4的坐标为(2,3),
∴M4的坐标为(1,0),
综上所述:满足条件的点M的坐标为(1,0)或(5,0)或(,0)或(﹣,0).
一、选择题(每小题有且只有一个正确答案,本题共10小题,每小题4分,共40分)
1.化简的正确结果是( )
A.±2 B.﹣2 C.2 D.4
2.下面四个图形,是中心对称图形的是( )
A. B. C. D.
3.如图所示在△ABC中,AB边上的高线画法正确的是( )
A. B.
C. D.
4.下列运算正确的是( )
A.(3m2)2=6m4 B.m2 m3=m5
C.3m﹣m=2 D.(m+1)2=m2+1
5.在2021年3月8日当天,由贾玲导演并主演的电影《你好,李焕英》,收获约46120000元票房,将46120000用科学记数法表示是( )
A.4612×104 B.4.612×108 C.46.12×106 D.4.612×107
6.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,11,13,15.关于这组数据,冉冉得出如下结果,其中错误的是( )
A.众数是11 B.平均数是12 C.方差是 D.中位数是13
7.实数a在数轴上的对应点的位置如图所示.若实数b满足﹣a<b<a,则b的值可以是( )
A.﹣3 B.﹣2 C.﹣1 D.2
8.直线y=x+a不经过第二象限,则关于x的方程ax2+2x+1=0实数解的个数是( )
A.0个 B.1个 C.2个 D.1个或2个
9.如图,在△ABC中,∠C=90°,点D在斜边AB上,且AD=CD,则下列结论中错误的结论是( )
A.∠DCB=∠B B.BC=BD
C.AD=BD D.∠ACD=∠BDC
10.如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2021次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2021次移动中,跳棋停留的顶点是( )
A.A B.B C.E D.G
二、填空题(本题共8小题,每小题4分,共32分)
11.使有意义的x的取值范围是 .
12.因式分解:3y2﹣12= .
13.若方程x2+kx﹣2=0的一个根是﹣2,则k的值是 .
14.如图:将一副直角三角板(∠A=30°,∠E=45°)按如图所示的位置摆放,使AB∥EF,则∠DOC的度数是 .
15.抗击“新冠肺炎”线上学习期间,某校为了解学校1000名九年级学生一周体育锻炼时间的情况,随机调查了50名九年级学生,并绘制成如图所示的条形统计图.根据图中数据,估计该校1000名九年级学生一周的体育锻炼时间不少于7小时的人数是 人.
16.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为 .
17.如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上.过点P分别作x轴、y轴的垂线,垂足分别为A、B,取线段OB的中点C,连接PC并延长交x轴于点D.则△APD的面积为 .
18.抛物线y=ax2+3ax+b的一部分图象如图,设该抛物线与x轴的交点为A(﹣5,0)和B,与y轴的交点为C,若△ACO∽△CBO,则∠CAB的正切值为 .
三、解答题(本题共7小题,共78分)
19.计算:.
20.先化简,再求值:,其中x=.
21.在平行四边形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BC=5,求CD的长.
22.驾驶员在驾驶车辆行驶过程中都会产生视觉盲区,如图,△ABC、△FED区域分别为该驾驶员在驾车行驶过程中的左右盲区,铅直高度AC、FD分别为盲高,BC、ED分别为盲宽,驾驶员视线PB与地面所在水平线BE的夹角∠PBE=45°,视线PE与地面BE的夹角∠PEB=30°,点A,F为视线与车窗底端的交点,AF∥BE,AC⊥BE,FD⊥BE.若点A到点B的距离AB=2m.
(1)求盲高AC;
(2)求右盲区△FED面积.
23.据新浪网调查,2019年全国网民最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图1所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题.
(1)求出图1中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年的年平均增长率约为多少?(≈3.16)
24.如图,矩形OABC的顶点A,C分别落在x轴,y轴的正半轴上,顶点B(2,2),反比例函数y=(x>0)的图象与BC,AB分别交于D,E,BD=.
(1)求反比例函数关系式和点E的坐标;
(2)写出DE与AC的位置关系并说明理由;
(3)点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点P是第一象限内抛物线上的动点.
(1)求抛物线的解析式;
(2)连接BC与OP,交于点D,求当的值最大时点P的坐标;
(3)点F是抛物线上的动点,在x轴上是否存在点M,使得以点B,C,M,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点M的坐标;如果不存在,请说明理由.
参考答案
一、选择题(每小题有且只有一个正确答案,本题共10小题,每小题4分,共40分)
1.化简的正确结果是( )
A.±2 B.﹣2 C.2 D.4
【分析】根据二次根式的基本性质进行化简求解即可.
解:=2.
故选:C.
2.下面四个图形,是中心对称图形的是( )
A. B. C. D.
【分析】根据中心对称图形的定义,结合选项所给图形进行判断即可.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
解:A.不是中心对称图形,故本选项不符合题意;
B.不是中心对称图形,故本选项不符合题意;
C.不是中心对称图形,故本选项不符合题意;
D.是中心对称图形,故本选项符合题意.
故选:D.
3.如图所示在△ABC中,AB边上的高线画法正确的是( )
A. B.
C. D.
【分析】直接利用高线的概念得出答案.
解:在△ABC中,AB边上的高线画法正确的是B,
故选:B.
4.下列运算正确的是( )
A.(3m2)2=6m4 B.m2 m3=m5
C.3m﹣m=2 D.(m+1)2=m2+1
【分析】根据完全平方公式、整式的乘法运算、乘方运算以及减法运算法则即可求出答案.
解:A、原式=9m4,故A不符合题意.
B、原式=m5,故B符合题意.
C、原式=2m,故C不符合题意.
D、原式=m2+2m+1,故D不符合题意.
故选:B.
5.在2021年3月8日当天,由贾玲导演并主演的电影《你好,李焕英》,收获约46120000元票房,将46120000用科学记数法表示是( )
A.4612×104 B.4.612×108 C.46.12×106 D.4.612×107
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,且n比原来的整数位数少1,据此判断即可.
解:46120000=4.612×107.
故选:D.
6.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,11,13,15.关于这组数据,冉冉得出如下结果,其中错误的是( )
A.众数是11 B.平均数是12 C.方差是 D.中位数是13
【分析】根据平均数、众数、中位数、方差的计算方法分别计算这组数据的平均数、众数、中位数、方差,最后做出选择.
解:数据11,10,11,13,11,13,15中,11出现的次数最多是3次,因此众数是11,于是A选项不符合题意;
将这7个数据从小到大排列后,处在中间位置的一个数是11,因此中位数是11,于是D符合题意;
=(11+10+11+13+11+13+15)÷7=12,即平均数是12,于是选项B不符合题意;
S2=[(10﹣12)2+(11﹣12)2×3+(13﹣12)2×2+(15﹣12)2]=,因此方差为,于是选项C不符合题意;
故选:D.
7.实数a在数轴上的对应点的位置如图所示.若实数b满足﹣a<b<a,则b的值可以是( )
A.﹣3 B.﹣2 C.﹣1 D.2
【分析】根据点b在数轴上的位置可求.
解:将﹣a,b在数轴上表示出来如下:
∵﹣a<b<a.
∴b在﹣a和a之间.
选项中只有﹣1符合条件.
故选:C.
8.直线y=x+a不经过第二象限,则关于x的方程ax2+2x+1=0实数解的个数是( )
A.0个 B.1个 C.2个 D.1个或2个
【分析】利用一次函数的性质得到a≤0,再判断Δ=22﹣4a>0,从而得到方程根的情况.
解:∵直线y=x+a不经过第二象限,
∴a≤0,
当a=0时,关于x的方程ax2+2x+1=0是一元一次方程,解为x=﹣,
当a<0时,关于x的方程ax2+2x+1=0是一元二次方程,
∵Δ=22﹣4a>0,
∴方程有两个不相等的实数根.
故选:D.
9.如图,在△ABC中,∠C=90°,点D在斜边AB上,且AD=CD,则下列结论中错误的结论是( )
A.∠DCB=∠B B.BC=BD
C.AD=BD D.∠ACD=∠BDC
【分析】根据等腰三角形的性质,可得∠A=∠ACD,再利用等角的余角相等得∠B=∠DCB,从而得DC=DB,然后可得AD=BD,然后逐一判断即可.
解:∵AD=CD,
∴∠A=∠ACD,
∵∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠BCD=90°,
∴∠B=∠BCD,
∴A正确,故A不符合题意;
∵∠BDC≠∠BCD,
∴BD≠BC,
∴B错误,故B符合题意;
∵∠B=∠BCD,
∴BD=DC,
∴AD=BD,
∴C正确,故C不符合题意;
∵∠BDC=∠A+∠ACD,∠A=∠ACD,
∴∠ACD=∠BDC,
∴D正确,故D不符合题意;
故选:B.
10.如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2021次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2021次移动中,跳棋停留的顶点是( )
A.A B.B C.E D.G
【分析】将棋子转圈的字母按顺序依次排成一列,然后找到循环的规律,即可解决.
解:根据题意可得,前7次移动后跳棋停留的顶点分别是B、D、G、D、B、A、A,
所以跳棋停留的顶点7次一个循环,
2021÷7=288……5,
故第2021次移动后停留的点是B,
故选:D.
二、填空题(本题共8小题,每小题4分,共32分)
11.使有意义的x的取值范围是 x≥1 .
【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.
解:∵有意义,
∴x﹣1≥0,解得x≥1.
故答案为:x≥1.
12.因式分解:3y2﹣12= 3(y+2)(y﹣2) .
【分析】先提取公因式3,再对余下的多项式利用平方差公式继续分解.
解:3y2﹣12,
=3(y2﹣4),
=3(y+2)(y﹣2).
13.若方程x2+kx﹣2=0的一个根是﹣2,则k的值是 1 .
【分析】将x=﹣2代入题目中的方程,即可求得k的值,本题得以解决.
解:∵一元二次方程x2+kx﹣2=0的一个根是﹣2,
∴(﹣2)2+k×(﹣2)﹣2=0,
解得,k=1,
故答案为:1.
14.如图:将一副直角三角板(∠A=30°,∠E=45°)按如图所示的位置摆放,使AB∥EF,则∠DOC的度数是 75° .
【分析】在Rt△DEF中由两角互余得∠F=45°,根据直线AB∥EF得∠A=∠ACF,再由三角形的内角和定理和邻补角的知识求出∠DOC=75°.
解:如图所示:
∵∠D=90°,
∴∠E+∠F=90°,
又∵∠E=45°,
∴∠F=45°,
又∵AB∥EF,
∴∠A=∠ACF,
又∵∠A=30°,
∴∠ACF=30°,
又∵∠ACF+∠F+∠1=180°,
∴∠1=105°,
又∵∠1+∠DOC=180°,
∴∠DOC=75°,
故答案为75°.
15.抗击“新冠肺炎”线上学习期间,某校为了解学校1000名九年级学生一周体育锻炼时间的情况,随机调查了50名九年级学生,并绘制成如图所示的条形统计图.根据图中数据,估计该校1000名九年级学生一周的体育锻炼时间不少于7小时的人数是 400 人.
【分析】用该校的总人数乘以一周的体育锻炼时间不少于7小时的人数所占的百分比即可.
解:根据题意得:1000×=400(人),
答:该校1000名九年级学生一周的体育锻炼时间不少于7小时的人数是400人;
故答案为:400.
16.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为 .
【分析】在△ABC中,由锐角三角函数求得AB,再由勾股定理求得BC,最后在△BCD中由锐角三角函数求得BD.
解:∵∠C=90°,AC=4,cosA=,
∴AB=5,
∴BC===3,
∵∠DBC=∠A.
∴cos∠DBC=cos∠A==,
∴BD=3×=,
故答案为:.
17.如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上.过点P分别作x轴、y轴的垂线,垂足分别为A、B,取线段OB的中点C,连接PC并延长交x轴于点D.则△APD的面积为 6 .
【分析】根据已知条件证得△PBC≌△DOC,再根据反比例函数系数k的几何意义即可得到结论.
解:∵PB⊥y轴,PA⊥x轴,
∴S矩形APBO=|k|=6,
在△PBC与△DOC中,
,
∴△PBC≌△DOC,
∴S△APD=S矩形APBO=6.
故答案为:6.
18.抛物线y=ax2+3ax+b的一部分图象如图,设该抛物线与x轴的交点为A(﹣5,0)和B,与y轴的交点为C,若△ACO∽△CBO,则∠CAB的正切值为 .
【分析】由对称轴可得点B的坐标,由于点C在y轴上,所以可写出点C的坐标,进而再由相似三角形对应边成比例求解点C的坐标,即可得出结论.
解:设B点的坐标为(x,0),
∵抛物线对称轴为直线x=﹣=﹣=﹣,
∴点B的横坐标为,
∴x=2,即B(2,0),
∴AO=5 BO=2.
∵△ACO∽△CBO,
∴,
∴,
∴OC=.
∴∠CAB的正切值=.
故答案为:.
三、解答题(本题共7小题,共78分)
19.计算:.
【分析】直接利用特殊角的三角函数值以及零指数幂的性质、绝对值的性质分别化简,进而计算得出答案.
解:原式=
=1﹣1+5
=5.
20.先化简,再求值:,其中x=.
【分析】根据分式的混合运算法则把原式化简,把x的值代入计算即可.
解:原式=(﹣)÷
=×
=,
当x=﹣1时,原式==.
21.在平行四边形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BC=5,求CD的长.
【分析】(1)由平行四边形的性质得到AB∥CD,AB=CD,推出四边形DFBE是平行四边形,根据矩形的判定定理即可得到结论;
(2)由矩形的性质得DE=BF,由角平分线的定义得到∠DCF=∠BCF,由平行线的性质得到∠DCF=∠CFB,证出BF=BC=5,进而得到结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形DFBE是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形DFBE是矩形;
(2)解:由(1)得:四边形DFBE是矩形,
∴DE=BF,
∵CF平分∠DCB,
∴∠DCF=∠BCF,
∵AB∥CD,
∴∠DCF=∠CFB,
∴∠BCF=∠CFB,
∴BF=BC=5,
∴DE=BF=5,
∴CD=DE+CE=5+3=8.
22.驾驶员在驾驶车辆行驶过程中都会产生视觉盲区,如图,△ABC、△FED区域分别为该驾驶员在驾车行驶过程中的左右盲区,铅直高度AC、FD分别为盲高,BC、ED分别为盲宽,驾驶员视线PB与地面所在水平线BE的夹角∠PBE=45°,视线PE与地面BE的夹角∠PEB=30°,点A,F为视线与车窗底端的交点,AF∥BE,AC⊥BE,FD⊥BE.若点A到点B的距离AB=2m.
(1)求盲高AC;
(2)求右盲区△FED面积.
【分析】(1)根据AC=AB sin45°求解即可;
(2)解直角三角形求出DE,DF,可得结论.
解:(1)∵FD⊥EB,AC⊥EB,
∴DF∥AC,
∵AF∥EB,
∴四边形ACDF是平行四边形,
∵∠ACD=90°,
∴四边形ACDF是矩形,
∴DF=AC,
在Rt△ACB中,∠ACB=90°,
∴AC=AB sin45°==(m),
(2)∵DF=AC=(m),
在Rt△DEF中,∠FDE=90°,
∴tan∠E=,
∴DE===(m).
所以右盲区△FED面积=××=(m2).
23.据新浪网调查,2019年全国网民最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图1所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题.
(1)求出图1中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年的年平均增长率约为多少?(≈3.16)
【分析】(1)求出反腐占的百分比,得到x的值;再由环保人数除以所占的百分比得到总人数,然后求出教育与反腐及其他的人数,补全条形统计图即可;
(2)设2017年到2019年的年平均增长率为x,则2018年网民最关注教育问题的人数所占百分比约为10%(1+x),2019年网民最关注教育问题的人数所占百分比约为10%(1+x)2,由2019年网民最关注教育问题的人数所占百分比约为25%,再由2019年网民最关注教育问题的人数所占百分比不变列出方程,解方程即可.
解:(1)关注“反腐”类问题的网民所占百分比为:1﹣15%﹣30%﹣25%﹣10%=20%,
∴x=20,
关注该五类热点问题网民的总人数为:140÷10%=1400(人),
则关注教育问题网民的人数为:1400×25%=350(人),
关注反腐问题网民的人数为:1400×20%=280(人),
关注其它问题网民的人数为:1400×15%=210(人),
补全条形统计图如下:
(2)设2017年到2019年的年平均增长率为x,
由题意得:10%(1+x)2=25%,
解得:x1≈0.58=58%,x2≈﹣2.58(不合题意,舍去).
答:从2017年到2019年的年平均增长率约为58%.
24.如图,矩形OABC的顶点A,C分别落在x轴,y轴的正半轴上,顶点B(2,2),反比例函数y=(x>0)的图象与BC,AB分别交于D,E,BD=.
(1)求反比例函数关系式和点E的坐标;
(2)写出DE与AC的位置关系并说明理由;
(3)点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.
【分析】(1)求出D(,2),再用待定系数法即可求解;
(2)证明=,即可求解;
(3)①当点F在点C的下方时,求出FH=1,CH=,求出点F(1,),则点G(3,),即可求解;②当点F在点C的上方时,同理可解.
解:(1)∵B(2,2),则BC=2,
而BD=,
∴CD=2﹣=,故点D(,2),
将点D的坐标代入反比例函数表达式得:2=,解得k=3,
故反比例函数表达式为y=,
当x=2时,y=,故点E(2,);
(2)由(1)知,D(,2),点E(2,),点B(2,2),
则BD=,BE=,
故==,===,
∴DE∥AC;
(3)①当点F在点C的下方时,
当点G在点F的右方时,如下图,
过点F作FH⊥y轴于点H,
∵四边形BCFG为菱形,则BC=CF=FG=BG=2,
在Rt△OAC中,OA=BC=2,OC=AB=2,
则tan∠OCA===,故∠OCA=30°,
则FH=FC=1,CH=CF cos∠OCA=2×=,
故点F(1,),则点G(3,),
当x=3时,y==,故点G在反比例函数图象上;
②当点F在点C的上方时,
同理可得,点G(1,3),
同理可得,点G在反比例函数图象上;
综上,点G的坐标为(3,)或(1,3)都在反比例函数图象上.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点P是第一象限内抛物线上的动点.
(1)求抛物线的解析式;
(2)连接BC与OP,交于点D,求当的值最大时点P的坐标;
(3)点F是抛物线上的动点,在x轴上是否存在点M,使得以点B,C,M,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点M的坐标;如果不存在,请说明理由.
【分析】(1)利用待定系数法可求解析式;
(2)过点P作PG⊥x轴,交BC与G,先求出直线BC的解析式,设点P(p,﹣p2+2p+3),则点G坐标为(p,﹣p+3),可求PG的长,由平行线分线段成比例可得=,利用二次函数的性质可求解;
(3)存在.由题意C(0,3),分图中三种情形,利用平行四边形的性质以及平移变换的性质求解即可.
解:(1)∵抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),
∴,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)如图1,过点P作PG⊥x轴,交BC于G,
∵抛物线的解析式为y=﹣x2+2x+3与y轴交于点C,
∴点C(0,3),
∴直线BC解析式为y=﹣x+3,
设点P(p,﹣p2+2p+3),则点G坐标为(p,﹣p+3),
∴PG=﹣p2+2p+3﹣(﹣p+3)=﹣p2+3p,
∵PG∥OC,
∴===﹣(p﹣)2+,
∴当p=时,的值有最大值,
∴点P(,);
(3)存在,满足条件的点M的坐标为(1,0)或(5,0)或(,0)或(﹣,0).理由如下:
设点M的坐标为(m,0),
当BC是平行四边形BCMF的边时,如图1,
点C(0,3)平移到点B(3,0),先向下平移3个单位,再向右平移3个单位,
则点M1(m,0),平移到F1(m+3,﹣3),
令﹣x2+2x+3=﹣3,可得m+3=1±;
∴m=﹣2±;
∴M1(﹣,0),M2(,0).
当BC是平行四边形BCFM的边时,如图2,
∴点B(3,0)平移到点C(0,3),先向上平移3个单位,再向左平移3个单位,
则点M1(m,0),平移到F1(m﹣3,3),
令﹣x2+2x+3=3,可得m﹣3=0或2;
∴m=3(舍)或m=5;
∴M3(5,0).
当BC是平行四边形BMCF的对角线时,BM∥CF,且BM=CF,
由上可知,点F4的坐标为(2,3),
∴M4的坐标为(1,0),
综上所述:满足条件的点M的坐标为(1,0)或(5,0)或(,0)或(﹣,0).
同课章节目录
