2021-2022学年山东省淄博市桓台县七年级(上)期末数学试卷(五四学制)(word解析版)
文档属性
| 名称 | 2021-2022学年山东省淄博市桓台县七年级(上)期末数学试卷(五四学制)(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 923.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 10:55:20 | ||
图片预览


文档简介
2021-2022学年山东省淄博市桓台县七年级第一学期期末数学试卷(五四学制)
一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分。在每小题所给出的四个选项中,只有一项是符合题目要求的)
1.已知三角形的两边长分别为2、10,则第三边长可能是( )
A.6 B.8 C.10 D.12
2.如图,已知△ABC中,AB=AC,点D、E分别在BC、AC上,AD=AE,∠BAD=∠CAD=20°,则∠EDC等于( )
A.30° B.20° C.10° D.5°
3.点A(m+1,3m﹣7)在第一、三象限的角平分线上,则m的值为( )
A.3 B.4 C.5 D.6
4.如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F.过点F作DE∥BC,交AB于点D,交AC于点E.若AB=4,AC=5,则△ADE的周长为( )
A.8 B.9 C.10 D.13
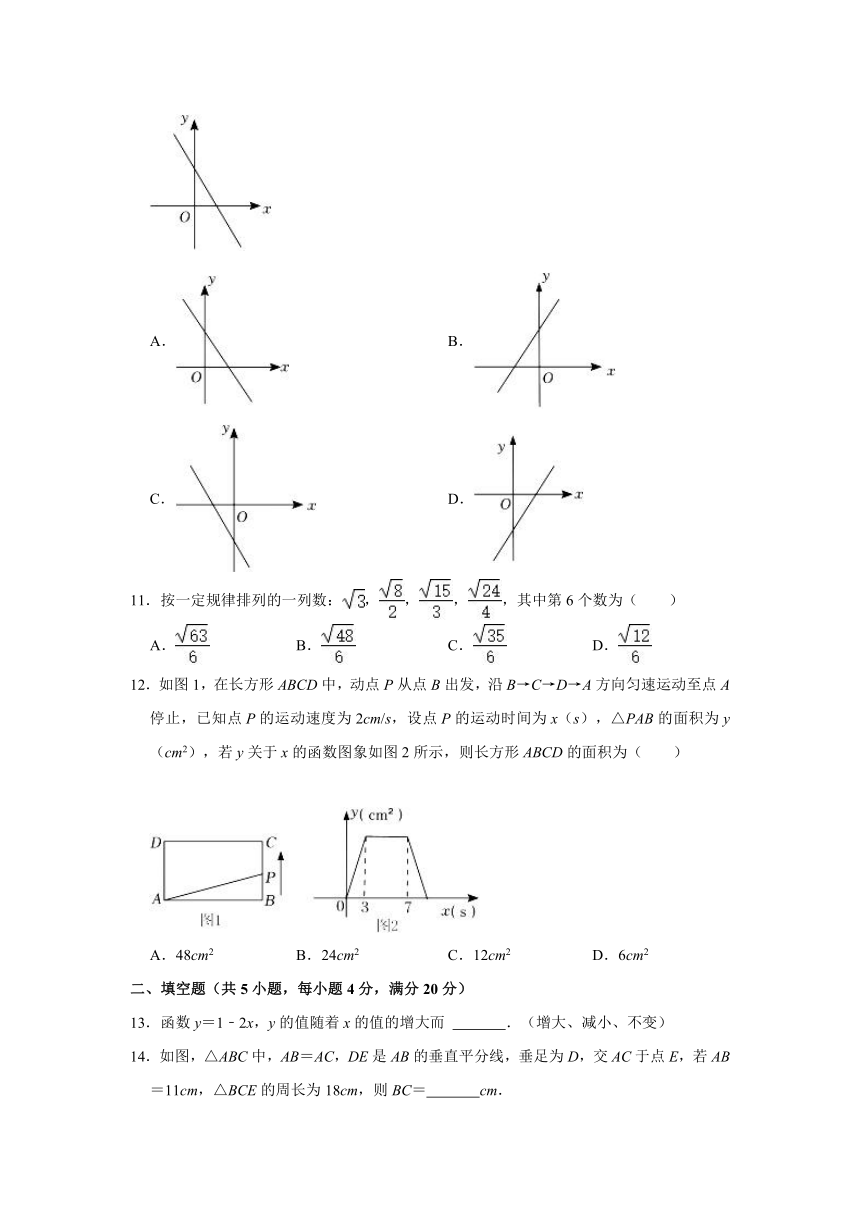
5.已知k<0,b<0,则一次函数y=kx+b的图象可能是( )
A. B.
C. D.
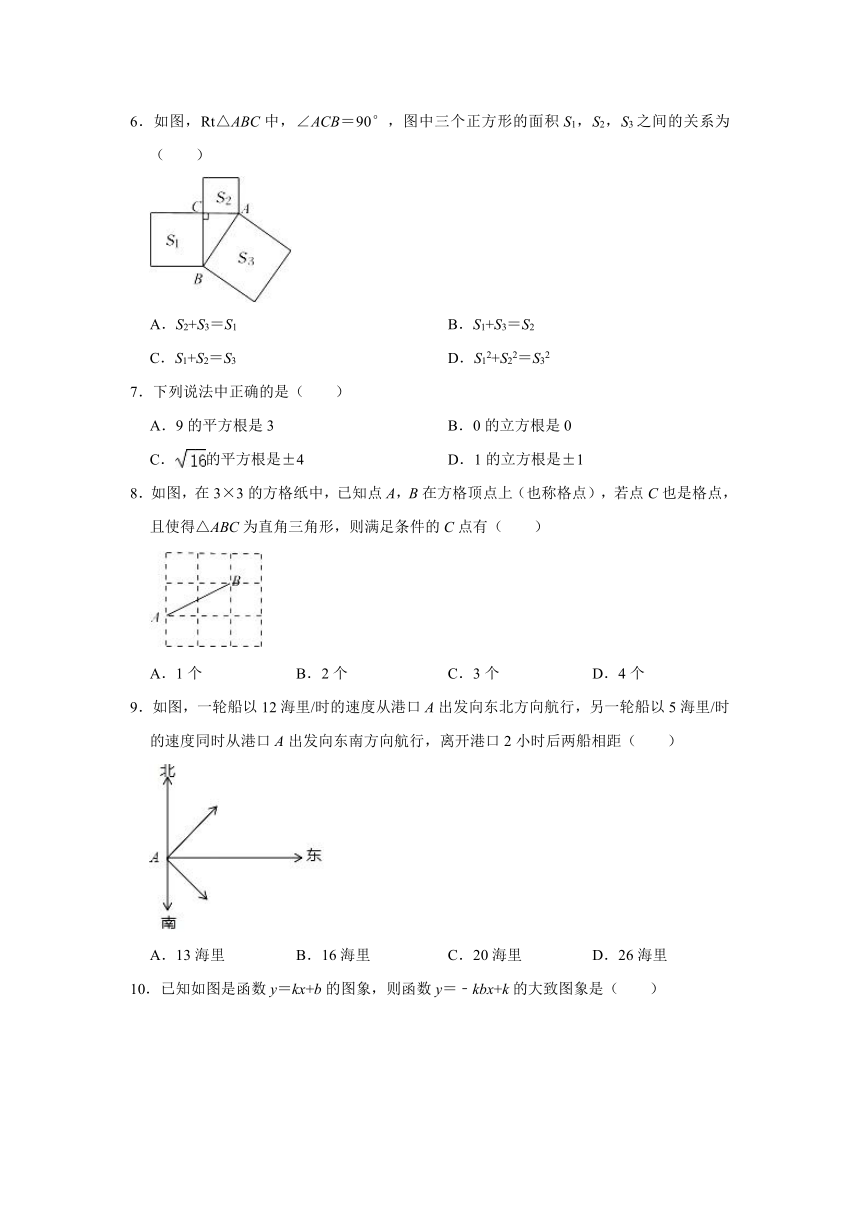
6.如图,Rt△ABC中,∠ACB=90°,图中三个正方形的面积S1,S2,S3之间的关系为( )
A.S2+S3=S1 B.S1+S3=S2
C.S1+S2=S3 D.S12+S22=S32
7.下列说法中正确的是( )
A.9的平方根是3 B.0的立方根是0
C.的平方根是±4 D.1的立方根是±1
8.如图,在3×3的方格纸中,已知点A,B在方格顶点上(也称格点),若点C也是格点,且使得△ABC为直角三角形,则满足条件的C点有( )
A.1个 B.2个 C.3个 D.4个
9.如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )
A.13海里 B.16海里 C.20海里 D.26海里
10.已知如图是函数y=kx+b的图象,则函数y=﹣kbx+k的大致图象是( )
A. B.
C. D.
11.按一定规律排列的一列数:,,,,其中第6个数为( )
A. B. C. D.
12.如图1,在长方形ABCD中,动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止,已知点P的运动速度为2cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),若y关于x的函数图象如图2所示,则长方形ABCD的面积为( )
A.48cm2 B.24cm2 C.12cm2 D.6cm2
二、填空题(共5小题,每小题4分,满分20分)
13.函数y=1﹣2x,y的值随着x的值的增大而 .(增大、减小、不变)
14.如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于点E,若AB=11cm,△BCE的周长为18cm,则BC= cm.
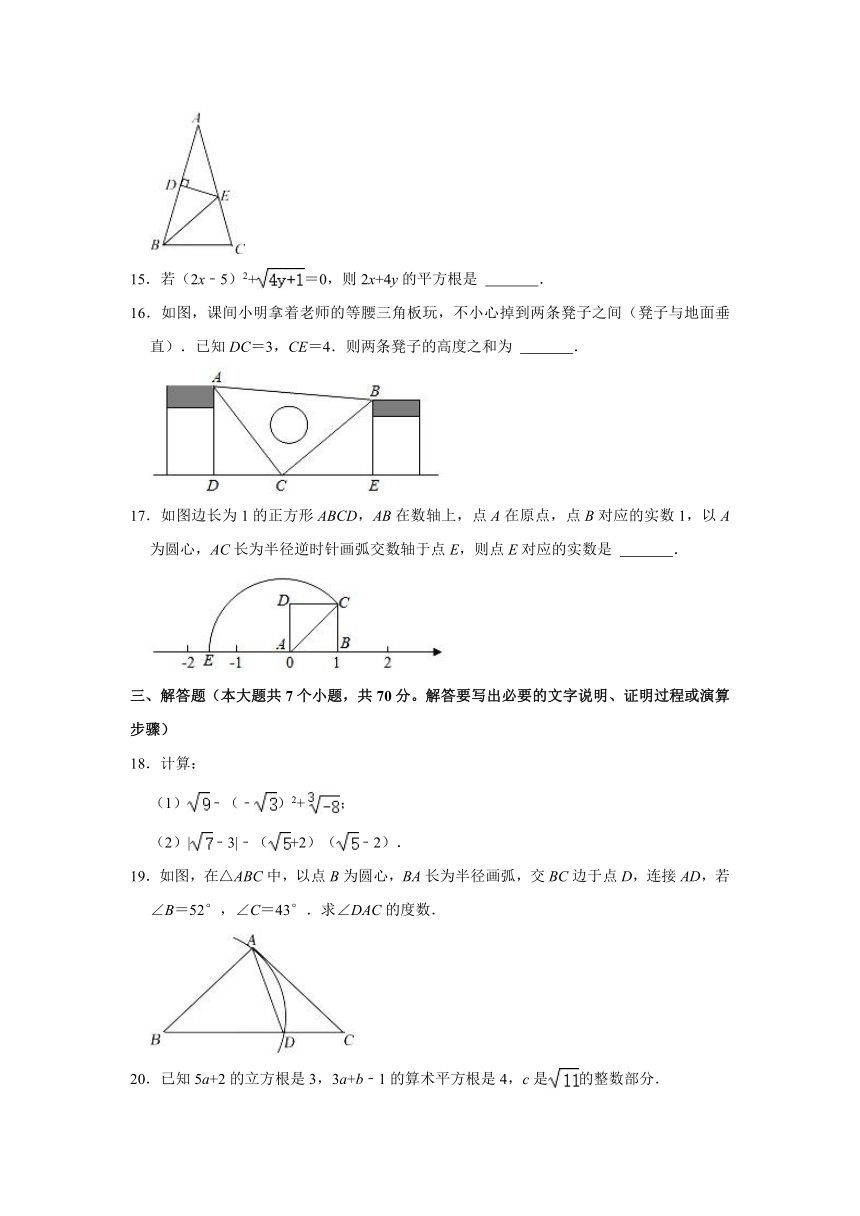
15.若(2x﹣5)2+=0,则2x+4y的平方根是 .
16.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4.则两条凳子的高度之和为 .
17.如图边长为1的正方形ABCD,AB在数轴上,点A在原点,点B对应的实数1,以A为圆心,AC长为半径逆时针画弧交数轴于点E,则点E对应的实数是 .
三、解答题(本大题共7个小题,共70分。解答要写出必要的文字说明、证明过程或演算步骤)
18.计算:
(1)﹣(﹣)2+;
(2)|﹣3|﹣(+2)(﹣2).
19.如图,在△ABC中,以点B为圆心,BA长为半径画弧,交BC边于点D,连接AD,若∠B=52°,∠C=43°.求∠DAC的度数.
20.已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
21.如图,△ABC的一个顶点A在△DEC的边DE上,AB交CD于点F,且AC=EC,∠1=∠2=∠3.试说明AB与DE的大小关系.
22.如图,在直角坐标系内,已知点A(﹣1,0).
(1)图中点B的坐标是 ;
(2)点B关于原点对称的点D的坐标是 ;点A关于y轴对称的点C的坐标是 ;
(3)四边形ABCD的面积是 ;
(4)在y轴上找一点F,使S△ADF=S△ABC.那么点F的坐标为 .
23.如图,平面直角坐标系中,直线l经过原点O和点A(6,4),经过点A的另一条直线交x轴于点B(12,0).
(1)求直线l的表达式;
(2)求△AOB的面积;
(3)在直线l上求点P,使S△ABP=S△AOB.
24.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求k1和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和k2的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.
参考答案
一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分。在每小题所给出的四个选项中,只有一项是符合题目要求的)
1.已知三角形的两边长分别为2、10,则第三边长可能是( )
A.6 B.8 C.10 D.12
【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解:设第三边长为xcm,根据三角形的三边关系可得:
10﹣2<x<10+2,
解得:8<x<12,
故选:C.
2.如图,已知△ABC中,AB=AC,点D、E分别在BC、AC上,AD=AE,∠BAD=∠CAD=20°,则∠EDC等于( )
A.30° B.20° C.10° D.5°
【分析】由题意易得△ABD≌△ACD,则有∠ADC=90°,再由AD=AE,从而可求∠ADE=80°,即可求∠EDC的度数.
解:在△ABD与△ACD中,
,
∴△ABD≌△ACD(SAS),
∴∠ADC=∠ADB=90°,
∵AD=AE,
∴∠ADE=∠AED,
∴∠ADE=(180°﹣∠CAD)=80°,
∴∠EDC=∠ADC﹣∠ADE=10°.
故选:C.
3.点A(m+1,3m﹣7)在第一、三象限的角平分线上,则m的值为( )
A.3 B.4 C.5 D.6
【分析】直接利用在第一、三象限的角平分线上,横纵坐标相等,进而得出答案.
解:∵点A(m+1,3m﹣7)在第一、三象限的角平分线上,
∴m+1=3m﹣7,
解得:m=4.
故选:B.
4.如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F.过点F作DE∥BC,交AB于点D,交AC于点E.若AB=4,AC=5,则△ADE的周长为( )
A.8 B.9 C.10 D.13
【分析】根据角平分线的定义得到∠ABF=∠FBC,∠ACF=∠FCB,平行线的性质得到∠BFD=∠FBC,∠CFE=∠FCB,等量代换得到∠ABF=∠BFD,∠ACF=∠CFE,根据等腰三角形的判定定理得到BD=FD,CE=FE,即可得到结论.
解:∵BF平分∠ABC,CF平分∠ACB,
∴∠ABF=∠FBC,∠ACF=∠FCB,
∵DE∥BC,
∴∠BFD=∠FBC,∠CFE=∠FCB,
∴∠ABF=∠BFD,∠ACF=∠CFE,
∴BD=FD,CE=FE,
∵AB=4,AC=5,
∴△ADE的周长为:AD+DE+AE=AD+OD+OE+AE=AD+BD+CE+AE=AB+AC=4+5=9.
故选:B.
5.已知k<0,b<0,则一次函数y=kx+b的图象可能是( )
A. B.
C. D.
【分析】根据一次函数的图象性质即可判断.
解:∵k<0,b<0,
∴一次函数的图象经过二、三、四象限,
故选:D.
6.如图,Rt△ABC中,∠ACB=90°,图中三个正方形的面积S1,S2,S3之间的关系为( )
A.S2+S3=S1 B.S1+S3=S2
C.S1+S2=S3 D.S12+S22=S32
【分析】根据题意和题目中的图形,可以发现S1=BC2,S3=AB2,S2=AC2,再根据勾股定理解答即可.
解:∵S1,S2,S3分别表示三个正方形的面积,
∴S1=BC2,S3=AB2,S2=AC2,
∵∠ACB=90°,
∴AC2+BC2=AB2,
∴S1+S2=S3,
故选:C.
7.下列说法中正确的是( )
A.9的平方根是3 B.0的立方根是0
C.的平方根是±4 D.1的立方根是±1
【分析】根据平方根、立方根的定义逐项进行判断即可.
解:9的平方根为±=±3,因此选项A不符合题意;
因为03=0,所以0的立方根为0,因此选项B符合题意;
=4,4的平方根为±2,因此选项C不符合题意;
因为13=1,所以1的立方根为1,因此选项D不符合题意;
故选:B.
8.如图,在3×3的方格纸中,已知点A,B在方格顶点上(也称格点),若点C也是格点,且使得△ABC为直角三角形,则满足条件的C点有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据题意,结合图形,分两种情况讨论:①AB为直角△ABC斜边;②AB为等腰直角△ABC其中的一条直角边.
解:如图,分情况讨论:
①AB为直角△ABC斜边时,符合条件的格点C点有2个;
②AB为直角△ABC其中的一条直角边时,符合条件的格点C点有1个.
故共有3个点,
故选:C.
9.如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )
A.13海里 B.16海里 C.20海里 D.26海里
【分析】根据方位角可知两船所走的方向正好构成了直角.然后根据路程=速度×时间,得两条船分别走了24,18.再根据勾股定理,即可求得两条船之间的距离.
解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
两小时后,两艘船分别行驶了12×2=24(海里),5×2=10(海里),
根据勾股定理得:=26(海里).
答:离开港口2小时后两船相距26海里,
故选:D.
10.已知如图是函数y=kx+b的图象,则函数y=﹣kbx+k的大致图象是( )
A. B.
C. D.
【分析】根据函数y=kx+b的图象确定k,b的取值范围,即可确定函数y=﹣kbx+k的大致图象.
解:由函数y=kx+b的图象可知k<0、b>0,
∴kb<0,
∴﹣kb>0,
∴函数y=﹣kbx+k的图象经过第一、三、四象限;
故选:D.
11.按一定规律排列的一列数:,,,,其中第6个数为( )
A. B. C. D.
【分析】观察这列数,得到分子和分母的规律,进而得到答案.
解:根据一列数:,,,可知,
第n个数分母是n,分子是(n+1)2﹣1的算术平方根,
据此可知:第6个数是=,
故选:B.
12.如图1,在长方形ABCD中,动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止,已知点P的运动速度为2cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),若y关于x的函数图象如图2所示,则长方形ABCD的面积为( )
A.48cm2 B.24cm2 C.12cm2 D.6cm2
【分析】根据△ABP的面积只与点P的位置有关,结合图2求出长方形的长和宽,再由矩形的面积公式计算即可.
【解答】解∵动点P从点B出发,沿BC、CD、DA运动至点A停止,
当点P在点B,C之间运动时,△ABP的面积随时间x的增大而增大,
由图2知,当x=3时,点P到达点C处,
∴BC=3×2=6(cm);
当点P运动到点C,D之间时,△ABP的面积不变,
由图2可知,点P从点C运动到点D所用时间为7﹣3=4(s),
∴CD=2×4=8(cm),
∴长方形ABCD的面积=8×6=48(cm2).
故选:A.
二、填空题(共5小题,每小题4分,满分20分)
13.函数y=1﹣2x,y的值随着x的值的增大而 减小 .(增大、减小、不变)
【分析】根据一次函数的性质进行解答即可.
解:∵k=﹣2<0,
∴y的值随着x的值的增大而减小,
故答案为:减小.
14.如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于点E,若AB=11cm,△BCE的周长为18cm,则BC= 7 cm.
【分析】先求出AC长,再根据线段垂直平分线的性质求出AE=BE,可得BE+CE=AE+CE=AC=AB,再根据△BCE的周长求出即可.
解:∵AB=11cm,
∴AC=AB=11cm,
∵DE是AB的垂直平分线,
∴AE=BE,
∴BE+CE=AE+CE=AC=AB=11cm,
∵△BCE的周长为18cm,
∴BC=18﹣11=7(cm).
故答案为:7.
15.若(2x﹣5)2+=0,则2x+4y的平方根是 ±2 .
【分析】根据非负数的性质可求出2x,4y的值,进而求出2x+4y的值,再求2x+4y的平方根即可.
解:∵(2x﹣5)2+=0,
∴2x﹣5=0,4y+1=0,
∴2x=5,4y=﹣1,
∴2x+4y=5﹣1=4,
∴2x+4y的平方根为±=±2,
故答案为:±2.
16.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4.则两条凳子的高度之和为 7 .
【分析】利用等腰三角形的性质结合全等三角形的判定方法得出即可.
解:由题意可得:∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
则∠DAC=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
故DC=BE=3,AD=CE=4,
则两条凳子的高度之和为:3+4=7.
故答案为:7.
17.如图边长为1的正方形ABCD,AB在数轴上,点A在原点,点B对应的实数1,以A为圆心,AC长为半径逆时针画弧交数轴于点E,则点E对应的实数是 ﹣ .
【分析】先利用勾股定理求出AC的长,即为AE的长,然后根据E在原点的左边求出数轴上的点E所对应的实数.
解:∵正方形ABCD的边长AD=1,
∴AC==,
∴AE=AC=,
∵点E在原点的左边,
∴点E所对应的实数为﹣,
故答案为:﹣.
三、解答题(本大题共7个小题,共70分。解答要写出必要的文字说明、证明过程或演算步骤)
18.计算:
(1)﹣(﹣)2+;
(2)|﹣3|﹣(+2)(﹣2).
【分析】(1)根据算术平方根,二次根式的性质,立方根的定义即可得出答案;
(2)根据绝对值,平方差公式化简即可得出答案.
解:(1)原式=3﹣3﹣2
=﹣2;
(2)原式=3﹣﹣[()2﹣22]
=3﹣﹣1
=2﹣.
19.如图,在△ABC中,以点B为圆心,BA长为半径画弧,交BC边于点D,连接AD,若∠B=52°,∠C=43°.求∠DAC的度数.
【分析】根据题意和等腰三角形的性质,可以求得∠BAD和∠BDA的度数,再根据三角形外角和内角的关系,即可求得∠DAC的度数.
解:∵∠B=52°,∠C=43°,
∴∠BAC=180°﹣∠B﹣∠C=85°,
由作图可知:BA=BD,
∴∠BAD=∠BDA=(180°﹣∠B)÷2=64°,
∴∠DAC=∠BAC﹣∠BAD=85°﹣64°=21°.
20.已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
【分析】(1)利用立方根的意义、算术平方根的意义、无理数的估算方法,求出a、b、c的值;
(2)将a、b、c的值代入代数式求出值后,进一步求得平方根即可.
解:(1)∵5a+2的立方根是3,3a+b﹣1的算术平方根是4,
∴5a+2=27,3a+b﹣1=16,
∴a=5,b=2;
∵,c是的整数部分,∴c=3;
(2)3a﹣b+c=15﹣2+3=16,16的平方根是±4.
21.如图,△ABC的一个顶点A在△DEC的边DE上,AB交CD于点F,且AC=EC,∠1=∠2=∠3.试说明AB与DE的大小关系.
【分析】由已知条件易证得∠B=∠D,∠BCA=∠DCE,利用AAS可证得△ABC≌△EDC,从而可得AB=ED.
解:∵∠1=∠2,∠AFD=∠BFC,
∴∠B=∠D,
又∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,
即∠BCA=∠DCE,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(AAS),
∴AB=ED.
22.如图,在直角坐标系内,已知点A(﹣1,0).
(1)图中点B的坐标是 (﹣3,4) ;
(2)点B关于原点对称的点D的坐标是 (3,﹣4) ;点A关于y轴对称的点C的坐标是 (1,0) ;
(3)四边形ABCD的面积是 8 ;
(4)在y轴上找一点F,使S△ADF=S△ABC.那么点F的坐标为 (0,4)或(0,﹣4) .
【分析】(1)根据坐标的意义即可得出点B的坐标;
(2)根据关于原点对称的两个点坐标之间的关系可得出点B关于原点对称的点C的坐标,同理根据关于y轴对称的两个点坐标之间的关系得出点A关于y对称点D的坐标;
(3)平行四边形ABCD的面积等于三角形ABD面积的2倍,根据坐标可求出三角形ABD的面积;
(4)三角形ABC的面积等于平行四边形ABCD面积的一半,也等于三角形ABD的面积,根据面积公式求出OF的长即可.
解:(1)过点B作x轴的垂线,垂足所对应的数为﹣3,因此点B的横坐标为﹣3,
过点B作y轴的垂线,垂足所对应的数为4,因此点B的纵坐标为4,
所以点B(﹣3,4);
故答案为:(﹣3,4);
(2)由于关于原点对称的两个点坐标纵横坐标均为互为相反数,
所以点B(﹣3,4)关于原点对称点C(3,﹣4),
由于关于y轴对称的两个点,其横坐标互为相反数,其纵坐标不变,
所以点A(﹣1,0)关于y轴对称点D(1,0),
故答案为:(3,﹣4),(1,0);
(3)S平行四边形ABCD=2S△ABD=2××2×4=8,
故答案为:8;
(4)因为S△ABC=S平行四边形ABCD=4=S△ADF,
所以AD OF=4,
∴OF=4,
又∵点F在y轴上,
∴点F(0,4)或(0,﹣4),
故答案为:(0,4)或(0,﹣4).
23.如图,平面直角坐标系中,直线l经过原点O和点A(6,4),经过点A的另一条直线交x轴于点B(12,0).
(1)求直线l的表达式;
(2)求△AOB的面积;
(3)在直线l上求点P,使S△ABP=S△AOB.
【分析】(1)设直线l的表达式为y=kx,把A(6,4)代入,利用待定系数法即可求解;
(2)根据三角形面积公式即可求解;
(3)设P点坐标为(x,x).当直线l上的点P使S△ABP=S△AOB时,分两种情况:①,点P在线段OA上;②点P在线段OA的延长线上.
解:(1)设直线l的表达式为y=kx,
把A(6,4)代入,得4=6k,
解得k=,
所以直线l的表达式为y=x;
(2)∵A(6,4),B(12,0),
∴△AOB的面积=×12×4=24;
(3)当直线l上的点P使S△ABP=S△AOB时,分两种情况:
设P点坐标为(x,x).
①如图1,点P在线段OA上,则AP=OA,
根据题意得,==,
解得x=4,
则P(4,);
②如图2,点P在线段OA的延长线上,则AP=OA,
根据题意得,==,
解得x=8,
则P(8,).
故所求P点坐标为(4,)或(8,).
24.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求k1和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和k2的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.
【分析】(1)把点(0,30),(10,180)代入y1=k1x+b,得到关于k1和b的二元一次方程组,求解即可;
(2)根据方案一每次健身费用按六折优惠,可得打折前的每次健身费用,再根据方案二每次健身费用按八折优惠,求出k2的值;
(3)将x=8分别代入y1、y2关于x的函数解析式,比较即可.
解:(1)∵y1=k1x+b过点(0,30),(10,180),
∴,解得,
k1=15表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元,
b=30表示的实际意义是:购买一张学生暑期专享卡的费用为30元;
(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),
则k2=25×0.8=20;
(3)选择方案一所需费用更少.理由如下:
由题意可知,y1=15x+30,y2=20x.
当健身8次时,
选择方案一所需费用:y1=15×8+30=150(元),
选择方案二所需费用:y2=20×8=160(元),
∵150<160,
∴选择方案一所需费用更少.
一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分。在每小题所给出的四个选项中,只有一项是符合题目要求的)
1.已知三角形的两边长分别为2、10,则第三边长可能是( )
A.6 B.8 C.10 D.12
2.如图,已知△ABC中,AB=AC,点D、E分别在BC、AC上,AD=AE,∠BAD=∠CAD=20°,则∠EDC等于( )
A.30° B.20° C.10° D.5°
3.点A(m+1,3m﹣7)在第一、三象限的角平分线上,则m的值为( )
A.3 B.4 C.5 D.6
4.如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F.过点F作DE∥BC,交AB于点D,交AC于点E.若AB=4,AC=5,则△ADE的周长为( )
A.8 B.9 C.10 D.13
5.已知k<0,b<0,则一次函数y=kx+b的图象可能是( )
A. B.
C. D.
6.如图,Rt△ABC中,∠ACB=90°,图中三个正方形的面积S1,S2,S3之间的关系为( )
A.S2+S3=S1 B.S1+S3=S2
C.S1+S2=S3 D.S12+S22=S32
7.下列说法中正确的是( )
A.9的平方根是3 B.0的立方根是0
C.的平方根是±4 D.1的立方根是±1
8.如图,在3×3的方格纸中,已知点A,B在方格顶点上(也称格点),若点C也是格点,且使得△ABC为直角三角形,则满足条件的C点有( )
A.1个 B.2个 C.3个 D.4个
9.如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )
A.13海里 B.16海里 C.20海里 D.26海里
10.已知如图是函数y=kx+b的图象,则函数y=﹣kbx+k的大致图象是( )
A. B.
C. D.
11.按一定规律排列的一列数:,,,,其中第6个数为( )
A. B. C. D.
12.如图1,在长方形ABCD中,动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止,已知点P的运动速度为2cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),若y关于x的函数图象如图2所示,则长方形ABCD的面积为( )
A.48cm2 B.24cm2 C.12cm2 D.6cm2
二、填空题(共5小题,每小题4分,满分20分)
13.函数y=1﹣2x,y的值随着x的值的增大而 .(增大、减小、不变)
14.如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于点E,若AB=11cm,△BCE的周长为18cm,则BC= cm.
15.若(2x﹣5)2+=0,则2x+4y的平方根是 .
16.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4.则两条凳子的高度之和为 .
17.如图边长为1的正方形ABCD,AB在数轴上,点A在原点,点B对应的实数1,以A为圆心,AC长为半径逆时针画弧交数轴于点E,则点E对应的实数是 .
三、解答题(本大题共7个小题,共70分。解答要写出必要的文字说明、证明过程或演算步骤)
18.计算:
(1)﹣(﹣)2+;
(2)|﹣3|﹣(+2)(﹣2).
19.如图,在△ABC中,以点B为圆心,BA长为半径画弧,交BC边于点D,连接AD,若∠B=52°,∠C=43°.求∠DAC的度数.
20.已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
21.如图,△ABC的一个顶点A在△DEC的边DE上,AB交CD于点F,且AC=EC,∠1=∠2=∠3.试说明AB与DE的大小关系.
22.如图,在直角坐标系内,已知点A(﹣1,0).
(1)图中点B的坐标是 ;
(2)点B关于原点对称的点D的坐标是 ;点A关于y轴对称的点C的坐标是 ;
(3)四边形ABCD的面积是 ;
(4)在y轴上找一点F,使S△ADF=S△ABC.那么点F的坐标为 .
23.如图,平面直角坐标系中,直线l经过原点O和点A(6,4),经过点A的另一条直线交x轴于点B(12,0).
(1)求直线l的表达式;
(2)求△AOB的面积;
(3)在直线l上求点P,使S△ABP=S△AOB.
24.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求k1和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和k2的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.
参考答案
一、选择题(请把正确选项填在表格中,本大题共12个小题,每小题5分,共计60分。在每小题所给出的四个选项中,只有一项是符合题目要求的)
1.已知三角形的两边长分别为2、10,则第三边长可能是( )
A.6 B.8 C.10 D.12
【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解:设第三边长为xcm,根据三角形的三边关系可得:
10﹣2<x<10+2,
解得:8<x<12,
故选:C.
2.如图,已知△ABC中,AB=AC,点D、E分别在BC、AC上,AD=AE,∠BAD=∠CAD=20°,则∠EDC等于( )
A.30° B.20° C.10° D.5°
【分析】由题意易得△ABD≌△ACD,则有∠ADC=90°,再由AD=AE,从而可求∠ADE=80°,即可求∠EDC的度数.
解:在△ABD与△ACD中,
,
∴△ABD≌△ACD(SAS),
∴∠ADC=∠ADB=90°,
∵AD=AE,
∴∠ADE=∠AED,
∴∠ADE=(180°﹣∠CAD)=80°,
∴∠EDC=∠ADC﹣∠ADE=10°.
故选:C.
3.点A(m+1,3m﹣7)在第一、三象限的角平分线上,则m的值为( )
A.3 B.4 C.5 D.6
【分析】直接利用在第一、三象限的角平分线上,横纵坐标相等,进而得出答案.
解:∵点A(m+1,3m﹣7)在第一、三象限的角平分线上,
∴m+1=3m﹣7,
解得:m=4.
故选:B.
4.如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F.过点F作DE∥BC,交AB于点D,交AC于点E.若AB=4,AC=5,则△ADE的周长为( )
A.8 B.9 C.10 D.13
【分析】根据角平分线的定义得到∠ABF=∠FBC,∠ACF=∠FCB,平行线的性质得到∠BFD=∠FBC,∠CFE=∠FCB,等量代换得到∠ABF=∠BFD,∠ACF=∠CFE,根据等腰三角形的判定定理得到BD=FD,CE=FE,即可得到结论.
解:∵BF平分∠ABC,CF平分∠ACB,
∴∠ABF=∠FBC,∠ACF=∠FCB,
∵DE∥BC,
∴∠BFD=∠FBC,∠CFE=∠FCB,
∴∠ABF=∠BFD,∠ACF=∠CFE,
∴BD=FD,CE=FE,
∵AB=4,AC=5,
∴△ADE的周长为:AD+DE+AE=AD+OD+OE+AE=AD+BD+CE+AE=AB+AC=4+5=9.
故选:B.
5.已知k<0,b<0,则一次函数y=kx+b的图象可能是( )
A. B.
C. D.
【分析】根据一次函数的图象性质即可判断.
解:∵k<0,b<0,
∴一次函数的图象经过二、三、四象限,
故选:D.
6.如图,Rt△ABC中,∠ACB=90°,图中三个正方形的面积S1,S2,S3之间的关系为( )
A.S2+S3=S1 B.S1+S3=S2
C.S1+S2=S3 D.S12+S22=S32
【分析】根据题意和题目中的图形,可以发现S1=BC2,S3=AB2,S2=AC2,再根据勾股定理解答即可.
解:∵S1,S2,S3分别表示三个正方形的面积,
∴S1=BC2,S3=AB2,S2=AC2,
∵∠ACB=90°,
∴AC2+BC2=AB2,
∴S1+S2=S3,
故选:C.
7.下列说法中正确的是( )
A.9的平方根是3 B.0的立方根是0
C.的平方根是±4 D.1的立方根是±1
【分析】根据平方根、立方根的定义逐项进行判断即可.
解:9的平方根为±=±3,因此选项A不符合题意;
因为03=0,所以0的立方根为0,因此选项B符合题意;
=4,4的平方根为±2,因此选项C不符合题意;
因为13=1,所以1的立方根为1,因此选项D不符合题意;
故选:B.
8.如图,在3×3的方格纸中,已知点A,B在方格顶点上(也称格点),若点C也是格点,且使得△ABC为直角三角形,则满足条件的C点有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据题意,结合图形,分两种情况讨论:①AB为直角△ABC斜边;②AB为等腰直角△ABC其中的一条直角边.
解:如图,分情况讨论:
①AB为直角△ABC斜边时,符合条件的格点C点有2个;
②AB为直角△ABC其中的一条直角边时,符合条件的格点C点有1个.
故共有3个点,
故选:C.
9.如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )
A.13海里 B.16海里 C.20海里 D.26海里
【分析】根据方位角可知两船所走的方向正好构成了直角.然后根据路程=速度×时间,得两条船分别走了24,18.再根据勾股定理,即可求得两条船之间的距离.
解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
两小时后,两艘船分别行驶了12×2=24(海里),5×2=10(海里),
根据勾股定理得:=26(海里).
答:离开港口2小时后两船相距26海里,
故选:D.
10.已知如图是函数y=kx+b的图象,则函数y=﹣kbx+k的大致图象是( )
A. B.
C. D.
【分析】根据函数y=kx+b的图象确定k,b的取值范围,即可确定函数y=﹣kbx+k的大致图象.
解:由函数y=kx+b的图象可知k<0、b>0,
∴kb<0,
∴﹣kb>0,
∴函数y=﹣kbx+k的图象经过第一、三、四象限;
故选:D.
11.按一定规律排列的一列数:,,,,其中第6个数为( )
A. B. C. D.
【分析】观察这列数,得到分子和分母的规律,进而得到答案.
解:根据一列数:,,,可知,
第n个数分母是n,分子是(n+1)2﹣1的算术平方根,
据此可知:第6个数是=,
故选:B.
12.如图1,在长方形ABCD中,动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止,已知点P的运动速度为2cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),若y关于x的函数图象如图2所示,则长方形ABCD的面积为( )
A.48cm2 B.24cm2 C.12cm2 D.6cm2
【分析】根据△ABP的面积只与点P的位置有关,结合图2求出长方形的长和宽,再由矩形的面积公式计算即可.
【解答】解∵动点P从点B出发,沿BC、CD、DA运动至点A停止,
当点P在点B,C之间运动时,△ABP的面积随时间x的增大而增大,
由图2知,当x=3时,点P到达点C处,
∴BC=3×2=6(cm);
当点P运动到点C,D之间时,△ABP的面积不变,
由图2可知,点P从点C运动到点D所用时间为7﹣3=4(s),
∴CD=2×4=8(cm),
∴长方形ABCD的面积=8×6=48(cm2).
故选:A.
二、填空题(共5小题,每小题4分,满分20分)
13.函数y=1﹣2x,y的值随着x的值的增大而 减小 .(增大、减小、不变)
【分析】根据一次函数的性质进行解答即可.
解:∵k=﹣2<0,
∴y的值随着x的值的增大而减小,
故答案为:减小.
14.如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于点E,若AB=11cm,△BCE的周长为18cm,则BC= 7 cm.
【分析】先求出AC长,再根据线段垂直平分线的性质求出AE=BE,可得BE+CE=AE+CE=AC=AB,再根据△BCE的周长求出即可.
解:∵AB=11cm,
∴AC=AB=11cm,
∵DE是AB的垂直平分线,
∴AE=BE,
∴BE+CE=AE+CE=AC=AB=11cm,
∵△BCE的周长为18cm,
∴BC=18﹣11=7(cm).
故答案为:7.
15.若(2x﹣5)2+=0,则2x+4y的平方根是 ±2 .
【分析】根据非负数的性质可求出2x,4y的值,进而求出2x+4y的值,再求2x+4y的平方根即可.
解:∵(2x﹣5)2+=0,
∴2x﹣5=0,4y+1=0,
∴2x=5,4y=﹣1,
∴2x+4y=5﹣1=4,
∴2x+4y的平方根为±=±2,
故答案为:±2.
16.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4.则两条凳子的高度之和为 7 .
【分析】利用等腰三角形的性质结合全等三角形的判定方法得出即可.
解:由题意可得:∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
则∠DAC=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
故DC=BE=3,AD=CE=4,
则两条凳子的高度之和为:3+4=7.
故答案为:7.
17.如图边长为1的正方形ABCD,AB在数轴上,点A在原点,点B对应的实数1,以A为圆心,AC长为半径逆时针画弧交数轴于点E,则点E对应的实数是 ﹣ .
【分析】先利用勾股定理求出AC的长,即为AE的长,然后根据E在原点的左边求出数轴上的点E所对应的实数.
解:∵正方形ABCD的边长AD=1,
∴AC==,
∴AE=AC=,
∵点E在原点的左边,
∴点E所对应的实数为﹣,
故答案为:﹣.
三、解答题(本大题共7个小题,共70分。解答要写出必要的文字说明、证明过程或演算步骤)
18.计算:
(1)﹣(﹣)2+;
(2)|﹣3|﹣(+2)(﹣2).
【分析】(1)根据算术平方根,二次根式的性质,立方根的定义即可得出答案;
(2)根据绝对值,平方差公式化简即可得出答案.
解:(1)原式=3﹣3﹣2
=﹣2;
(2)原式=3﹣﹣[()2﹣22]
=3﹣﹣1
=2﹣.
19.如图,在△ABC中,以点B为圆心,BA长为半径画弧,交BC边于点D,连接AD,若∠B=52°,∠C=43°.求∠DAC的度数.
【分析】根据题意和等腰三角形的性质,可以求得∠BAD和∠BDA的度数,再根据三角形外角和内角的关系,即可求得∠DAC的度数.
解:∵∠B=52°,∠C=43°,
∴∠BAC=180°﹣∠B﹣∠C=85°,
由作图可知:BA=BD,
∴∠BAD=∠BDA=(180°﹣∠B)÷2=64°,
∴∠DAC=∠BAC﹣∠BAD=85°﹣64°=21°.
20.已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
【分析】(1)利用立方根的意义、算术平方根的意义、无理数的估算方法,求出a、b、c的值;
(2)将a、b、c的值代入代数式求出值后,进一步求得平方根即可.
解:(1)∵5a+2的立方根是3,3a+b﹣1的算术平方根是4,
∴5a+2=27,3a+b﹣1=16,
∴a=5,b=2;
∵,c是的整数部分,∴c=3;
(2)3a﹣b+c=15﹣2+3=16,16的平方根是±4.
21.如图,△ABC的一个顶点A在△DEC的边DE上,AB交CD于点F,且AC=EC,∠1=∠2=∠3.试说明AB与DE的大小关系.
【分析】由已知条件易证得∠B=∠D,∠BCA=∠DCE,利用AAS可证得△ABC≌△EDC,从而可得AB=ED.
解:∵∠1=∠2,∠AFD=∠BFC,
∴∠B=∠D,
又∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,
即∠BCA=∠DCE,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(AAS),
∴AB=ED.
22.如图,在直角坐标系内,已知点A(﹣1,0).
(1)图中点B的坐标是 (﹣3,4) ;
(2)点B关于原点对称的点D的坐标是 (3,﹣4) ;点A关于y轴对称的点C的坐标是 (1,0) ;
(3)四边形ABCD的面积是 8 ;
(4)在y轴上找一点F,使S△ADF=S△ABC.那么点F的坐标为 (0,4)或(0,﹣4) .
【分析】(1)根据坐标的意义即可得出点B的坐标;
(2)根据关于原点对称的两个点坐标之间的关系可得出点B关于原点对称的点C的坐标,同理根据关于y轴对称的两个点坐标之间的关系得出点A关于y对称点D的坐标;
(3)平行四边形ABCD的面积等于三角形ABD面积的2倍,根据坐标可求出三角形ABD的面积;
(4)三角形ABC的面积等于平行四边形ABCD面积的一半,也等于三角形ABD的面积,根据面积公式求出OF的长即可.
解:(1)过点B作x轴的垂线,垂足所对应的数为﹣3,因此点B的横坐标为﹣3,
过点B作y轴的垂线,垂足所对应的数为4,因此点B的纵坐标为4,
所以点B(﹣3,4);
故答案为:(﹣3,4);
(2)由于关于原点对称的两个点坐标纵横坐标均为互为相反数,
所以点B(﹣3,4)关于原点对称点C(3,﹣4),
由于关于y轴对称的两个点,其横坐标互为相反数,其纵坐标不变,
所以点A(﹣1,0)关于y轴对称点D(1,0),
故答案为:(3,﹣4),(1,0);
(3)S平行四边形ABCD=2S△ABD=2××2×4=8,
故答案为:8;
(4)因为S△ABC=S平行四边形ABCD=4=S△ADF,
所以AD OF=4,
∴OF=4,
又∵点F在y轴上,
∴点F(0,4)或(0,﹣4),
故答案为:(0,4)或(0,﹣4).
23.如图,平面直角坐标系中,直线l经过原点O和点A(6,4),经过点A的另一条直线交x轴于点B(12,0).
(1)求直线l的表达式;
(2)求△AOB的面积;
(3)在直线l上求点P,使S△ABP=S△AOB.
【分析】(1)设直线l的表达式为y=kx,把A(6,4)代入,利用待定系数法即可求解;
(2)根据三角形面积公式即可求解;
(3)设P点坐标为(x,x).当直线l上的点P使S△ABP=S△AOB时,分两种情况:①,点P在线段OA上;②点P在线段OA的延长线上.
解:(1)设直线l的表达式为y=kx,
把A(6,4)代入,得4=6k,
解得k=,
所以直线l的表达式为y=x;
(2)∵A(6,4),B(12,0),
∴△AOB的面积=×12×4=24;
(3)当直线l上的点P使S△ABP=S△AOB时,分两种情况:
设P点坐标为(x,x).
①如图1,点P在线段OA上,则AP=OA,
根据题意得,==,
解得x=4,
则P(4,);
②如图2,点P在线段OA的延长线上,则AP=OA,
根据题意得,==,
解得x=8,
则P(8,).
故所求P点坐标为(4,)或(8,).
24.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求k1和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和k2的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.
【分析】(1)把点(0,30),(10,180)代入y1=k1x+b,得到关于k1和b的二元一次方程组,求解即可;
(2)根据方案一每次健身费用按六折优惠,可得打折前的每次健身费用,再根据方案二每次健身费用按八折优惠,求出k2的值;
(3)将x=8分别代入y1、y2关于x的函数解析式,比较即可.
解:(1)∵y1=k1x+b过点(0,30),(10,180),
∴,解得,
k1=15表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元,
b=30表示的实际意义是:购买一张学生暑期专享卡的费用为30元;
(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),
则k2=25×0.8=20;
(3)选择方案一所需费用更少.理由如下:
由题意可知,y1=15x+30,y2=20x.
当健身8次时,
选择方案一所需费用:y1=15×8+30=150(元),
选择方案二所需费用:y2=20×8=160(元),
∵150<160,
∴选择方案一所需费用更少.
同课章节目录
