2021-2022学年山东省济南市莱芜区八年级(上)期末数学试卷(五四学制)(word解析版)
文档属性
| 名称 | 2021-2022学年山东省济南市莱芜区八年级(上)期末数学试卷(五四学制)(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 11:31:17 | ||
图片预览



文档简介
2021-2022学年山东省济南市莱芜区八年级第一学期期末数学试卷(五四学制)
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂写在答题卡上,每小题选对得4分,选错、不选或选出的答案超过一个均记0分,共48分)
1.分解因式4x2﹣y2的结果是( )
A.(4x+y)(4x﹣y) B.4(x+y)(x﹣y)
C.(2x+y)(2x﹣y) D.2(x+y)(x﹣y)
2.下列分式中是最简分式的是( )
A. B.
C. D.
3.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数(单位:分)及方差s2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
甲 乙 丙 丁
6 7 7 6
s2 1 1.1 1 1.6
A.甲 B.乙 C.丙 D.丁
4.京剧脸谱、剪纸等图案蕴含着简洁美对称美,下面选取的图片中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
5.在对一组样本数据进行分析时,小月列出了方差的计算公式:s2=,由公式提供的信息,则下列说法错误的是( )
A.样本的众数是3 B.样本的中位数是2.5
C.样本的平均数是3 D.n=4
6.如果一个多边形的内角和是它的外角和的5倍,则这个多边形是( )
A.十边形 B.十一边形 C.十二边形 D.十三边形
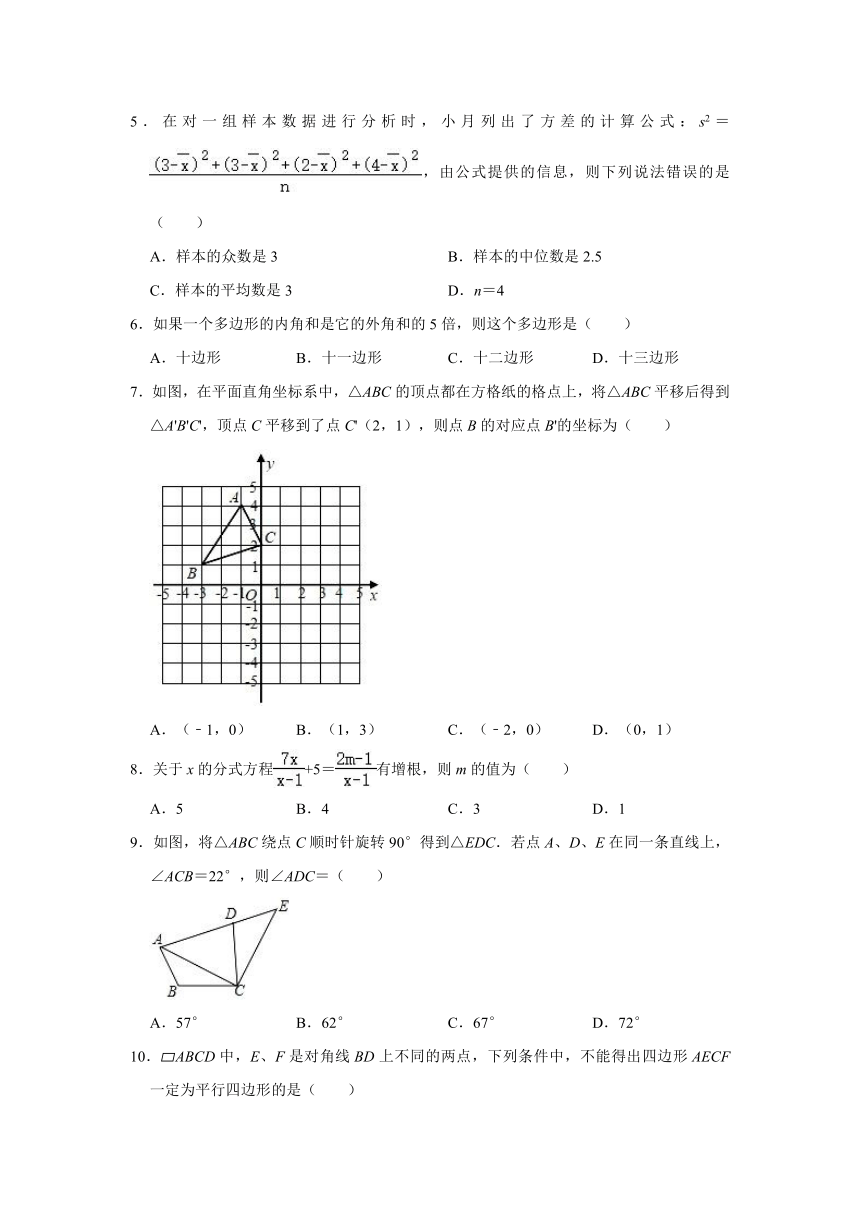
7.如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,将△ABC平移后得到△A'B'C',顶点C平移到了点C'(2,1),则点B的对应点B'的坐标为( )
A.(﹣1,0) B.(1,3) C.(﹣2,0) D.(0,1)
8.关于x的分式方程+5=有增根,则m的值为( )
A.5 B.4 C.3 D.1
9.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,∠ACB=22°,则∠ADC=( )
A.57° B.62° C.67° D.72°
10. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
11.某班学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了15分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的平均速度是骑车同学速度的3倍,设骑车同学的平均速度是x千米/小时,则下列方程正确的是( )
A. B.
C. D.
12.在 ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①GN=NE;②AE⊥GF;③AC平分∠BCD;④AC⊥BD,其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题填对得4分,共24分。请填在答题卡上)
13.分解因式:a3﹣2a2+a= .
14.化简的结果是 .
15.“阳光小区”开展“节约用水,从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较,统计出节水情况如表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 3 2 3 1 1
那么这10个家庭的节水量(m3)的平均数是 .
16.如图,已知 ABCD的周长为38,对角线AC、BD相交于点O,点E是CD的中点,△DOE的周长为16,则BD的长为 .
17.在平面直角坐标系中,点A的坐标为(0,6)点B的坐标为(2,4),△OAB沿x轴向右平移后得到△EDF,点B的对应点F是直线y=x上的一点,则点A的对应点D点的坐标为 .
18.已知:有理数a≠1,我们把称为a的差倒数.例如:2的差倒数是=﹣1,﹣1的差倒数是.如果a1=,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,那么a1 a2…a2022= .
三、解答题(本大题共9小题,共78分,解答要写出必要的文字说明、证明过程或推演步骤)
19.解方程:+=4.
20.先化简再求值:(﹣1)÷,其中a=1.
21.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
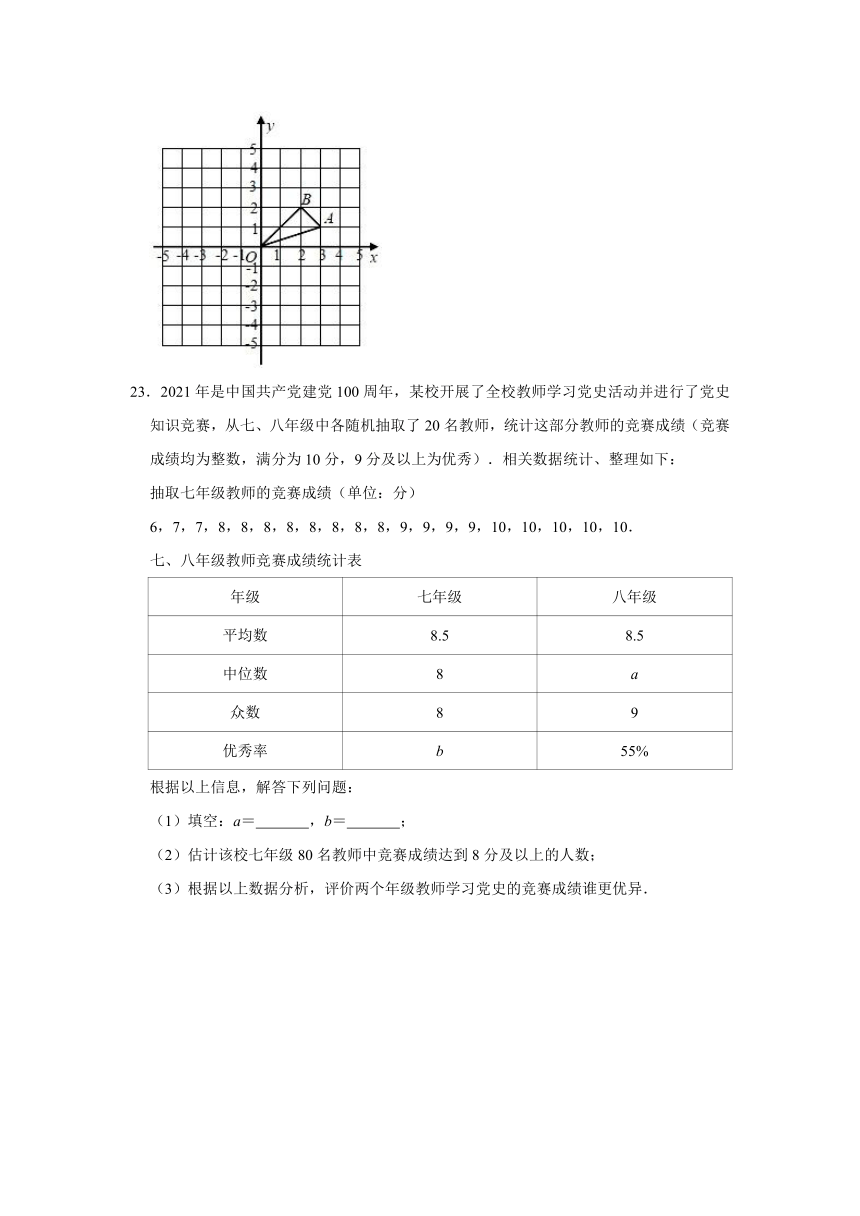
22.已知△OAB在平面直角坐标系中的位置如图所示,请解答以下问题:
(1)按要求作图:
先将△OAB绕原点O逆时针旋转90°,得到△OA1B1,再作出△OA2B2,使它与△OA1B1关于原点成中心对称;
(2)直接写出点A1的坐标 ;点B2的坐标 .
23.2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:
抽取七年级教师的竞赛成绩(单位:分)
6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10.
七、八年级教师竞赛成绩统计表
年级 七年级 八年级
平均数 8.5 8.5
中位数 8 a
众数 8 9
优秀率 b 55%
根据以上信息,解答下列问题:
(1)填空:a= ,b= ;
(2)估计该校七年级80名教师中竞赛成绩达到8分及以上的人数;
(3)根据以上数据分析,评价两个年级教师学习党史的竞赛成绩谁更优异.
24.如图,已知△ABC中,AB=AC,将△ABC绕点A沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=1,∠BAC=45°,当四边形ADFC是平行四边形时,求EC的长.
25.某生态示范园积极响应政府提出的“践行生态有机理念,推动有机农业发展”经济政策,培育优良品种,种植了多种有机水果.某超市从该示范园第一次用300元购进甲种水果,300元购进乙种水果.乙种水果的进价是甲种水果进价的1.5倍,超市所进甲种水果比所进乙种水果多10kg.
(1)求甲、乙两种水果的进价分别是每千克多少元?
(2)第一次购进的水果很快销售完毕,为满足消费者需求,该超市准备再次购进甲,乙两种有机水果共100千克,其中甲种水果的质量不少于乙种水果质量的3倍.若甲种水果的售价为13元/千克,乙种水果的售价为20元/千克,超市购进两种有机水果各多少千克时第二次获得最大利润,最大利润是多少?
26.点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
27.(1)如图1,△ABC和△AMN都是等腰直角三角形,直角顶点为点A,△ABC固定不动,△AMN可以绕着点A旋转.
①如图2,将△AMN绕点A旋转,使点M落在BC边上,连接CN.
直接写出图中的全等三角形: ;直接写出线段CN,CM,CB之间满足的等量关系为: ;
②如图2,试探索线段MA,MB,MC之间满足的等量关系,并完整地证明你的结论;
(2)如图3,P是等腰直角△ABC内一点,∠BAC=90°,连接PA,PB,PC,将△BAP绕点A顺时针旋转90°后得到△CAQ,连接PQ.已知PA=2,PB=3,若∠PQC=90°,求PC的长.
参考答案
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂写在答题卡上,每小题选对得4分,选错、不选或选出的答案超过一个均记0分,共48分)
1.分解因式4x2﹣y2的结果是( )
A.(4x+y)(4x﹣y) B.4(x+y)(x﹣y)
C.(2x+y)(2x﹣y) D.2(x+y)(x﹣y)
【分析】直接利用平方差公式分解因式得出答案.
解:4x2﹣y2=(2x+y)(2x﹣y).
故选:C.
2.下列分式中是最简分式的是( )
A. B.
C. D.
【分析】利用最简分式定义:分子分母没有公因式的分式,判断即可.
解:A.该分式符合最简分式的定义,符合题意;
B.该分式的分子、分母中含有公因式(x﹣1),不是最简分式,不符合题意
C.该分式的分子、分母中含有公因式(x+1),不是最简分式,不符合题意;
D.该分式的分子、分母中含有公因式(x﹣1),不是最简分式,不符合题意;
故选:A.
3.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数(单位:分)及方差s2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
甲 乙 丙 丁
6 7 7 6
s2 1 1.1 1 1.6
A.甲 B.乙 C.丙 D.丁
【分析】先比较平均数得到乙组和丙组成绩较好,然后比较方差得到丙组的状态稳定,于是可决定选丙组去参赛.
解:因为乙组、丙组的平均数比甲组、丁组大,而丙组的方差比乙组的小,
所以丙组的成绩比较稳定,
所以丙组的成绩较好且状态稳定,应选的组是丙组.
故选:C.
4.京剧脸谱、剪纸等图案蕴含着简洁美对称美,下面选取的图片中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.是轴对称图形,不是中心对称图形,故本选项不合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.不是轴对称图形,是中心对称图形,故本选项不合题意;
D.既是轴对称图形又是中心对称图形,故本选项符合题意.
故选:D.
5.在对一组样本数据进行分析时,小月列出了方差的计算公式:s2=,由公式提供的信息,则下列说法错误的是( )
A.样本的众数是3 B.样本的中位数是2.5
C.样本的平均数是3 D.n=4
【分析】根据方差的计算公式得出数据为2、3、3、4,再利用众数、中位数、平均数的定义求解即可.
解:由题意知,这组数据2、3、3、4,
所以样本的众数是3,中位数是=3,平均数为=3,n=4,
故选:B.
6.如果一个多边形的内角和是它的外角和的5倍,则这个多边形是( )
A.十边形 B.十一边形 C.十二边形 D.十三边形
【分析】根据多边形的内角和公式、外角和公式,可得方程,根据解方程,可得答案.
解:设这个多边形是n边形,由题意,得
(n﹣2)×180°=5×360°.
解得n=12,
故选:C.
7.如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,将△ABC平移后得到△A'B'C',顶点C平移到了点C'(2,1),则点B的对应点B'的坐标为( )
A.(﹣1,0) B.(1,3) C.(﹣2,0) D.(0,1)
【分析】根据上下平移横坐标不变,纵坐标上加下减,可得结论.
解:∵顶点C(0,2)平移到了点C'(2,1),
∴,△ABC向右平移了2﹣2=2个单位,向下平移了2﹣1=1个单位,
∴点B(﹣3,1)向右平移2个单位,向下平移1个单位,
得到B'(﹣1,0),
故选:A.
8.关于x的分式方程+5=有增根,则m的值为( )
A.5 B.4 C.3 D.1
【分析】根据分式方程的解法即可求出答案.
解:7x+5(x﹣1)=2m﹣1
x=
由题意可知:x=代入x﹣1=0,
﹣1=0
解得:m=4
故选:B.
9.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,∠ACB=22°,则∠ADC=( )
A.57° B.62° C.67° D.72°
【分析】由旋转的性质可得CA=CE,∠ACE=90°,∠ACB=∠DCE=22°,从而得△ACE是等腰直角三角形,进而得∠E=45°,最后利用∠ADC是△CDE的外角即可解答.
解:由旋转可得:
∠ACB=∠DCE=22°,CA=CE,∠ACE=90°,
∴△ACE是等腰直角三角形,
∴∠E=45°,
∵∠ADC是△CDE的一个外角,
∴∠ADC=∠E+∠DCE=45°+22°=67°,
故选:C.
10. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
【分析】连接AC与BD相交于O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,再根据对角线互相平分的四边形是平行四边形,只要证明得到OE=OF即可,然后根据各选项的条件分析判断即可得解.
解:如图,连接AC与BD相交于O,
在 ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
C、若CE=AF,则无法判断OE=OE,故本选项符合题意;
D、由∠DAF=∠BCE,从而推出△DAF≌△BCE,然后得出∠DFA=∠BEC,∴∠AFE=∠CEF,∴AF∥CE,结合选项B可证明四边形AECF是平行四边形;故本选项不符合题意;
故选:C.
11.某班学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了15分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的平均速度是骑车同学速度的3倍,设骑车同学的平均速度是x千米/小时,则下列方程正确的是( )
A. B.
C. D.
【分析】关键描述语:“过了15分钟后,其余同学乘汽车出发,结果他们同时到达”;等量关系为:骑自行车同学所用时间﹣乘车同学所用时间=.
解:设骑车学生的平均速度为xkm/h,则汽车的平均速度为3xkm/h.
根据题意,列方程得.
故选:B.
12.在 ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①GN=NE;②AE⊥GF;③AC平分∠BCD;④AC⊥BD,其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】通过证明四边形BGFE是平行四边形,可得GN=NE,故①正确;由等腰三角形的性质可得BE⊥AC,由平行四边形的性质可证GF⊥AE,故②正确;由外角的性质可得∠BOC>∠ACD,由等腰三角形的性质可得∠BOC=∠BCO≠∠ACD,故③错误;由等腰三角形的性质可得BE⊥AE,可得∠BOE<90°,则AC与BD不垂直,故④错误,即可求解.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E、F、G分别是OC、OD、AB的中点,
∴CD=2EF,EF∥CD,AB=2BG,
∴BG=EF,AB∥EF∥CD,
∴四边形BGFE是平行四边形,
∴GN=NE,故①正确;
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD=BC,
∵BD=2AD=2BC,
∴BO=BC,
又∵点E是OC的中点,
∴BE⊥AC,
∵四边形BGFE是平行四边形,
∴GF∥BE,
∴GF⊥AC,
即GF⊥AE,故②正确;
∵BO=BC,
∴∠BOC=∠BCO,
∵∠BOC=∠ACD+∠BDC,
∴∠BOC>∠ACD,
∴∠BCO≠∠ACD,
∴AC不平分∠BCD,故③错误;
∵BO=BC,点E是OC的中点,
∴BE⊥AC,
∴∠BOE<90°,
∴AC与BD不垂直,故④错误,
故选:B.
二、填空题(本大题共6小题,每小题填对得4分,共24分。请填在答题卡上)
13.分解因式:a3﹣2a2+a= a(a﹣1)2 .
【分析】此多项式有公因式,应先提取公因式a,再对余下的多项式进行观察,有3项,可利用完全平方公式继续分解.
解:a3﹣2a2+a
=a(a2﹣2a+1)
=a(a﹣1)2.
故答案为:a(a﹣1)2.
14.化简的结果是 .
【分析】直接将原式通分,进而利用分式的加减运算法则计算得出答案.
解:原式=+
=
=.
故答案为:.
15.“阳光小区”开展“节约用水,从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较,统计出节水情况如表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 3 2 3 1 1
那么这10个家庭的节水量(m3)的平均数是 0.45 .
【分析】根据加权平均数的计算公式即可求出答案.
解:根据题意得:
(0.3×3+0.4×2+0.5×3+0.6×1+0.7×1)=0.45(m3),
答:这10个家庭的节水量(m3)的平均数是0.45m3.
故答案为:0.45.
16.如图,已知 ABCD的周长为38,对角线AC、BD相交于点O,点E是CD的中点,△DOE的周长为16,则BD的长为 13 .
【分析】根据平行四边形的性质知O为BD的中点,即可判断OE是△DBC的中位线,即OE=BC,从而得出△BCD的周长是△DOE的周长的二倍,再根据BC+CD是平行四边形周长的一半求出BD的长即可.
解:∵四边形ABCD是平行四边形,且周长为38,
∴O是BD的中点,BC+CD=38×=19,
∵点E是CD的中点,
∴OE是△DBC的中位线,
∴△BCD的周长是△DOE的周长的2倍,
即BD+BC+DC=2(OD+OE+ED)=2×16,
∴BD+19=32,
解得:BD=13,
故答案为:13.
17.在平面直角坐标系中,点A的坐标为(0,6)点B的坐标为(2,4),△OAB沿x轴向右平移后得到△EDF,点B的对应点F是直线y=x上的一点,则点A的对应点D点的坐标为 (5,6) .
【分析】根据平移的性质知BF=AD.由一次函数图象上点的坐标特征可以求得点F的坐标,所以根据两点间的距离公式可以求得线段BF的长度,即AD的长度.
解:∵点A的坐标为(0,6)点B的坐标为(2,4),△OAB沿x轴向右平移后得到△EDF,
∴点D的纵坐标是6,点F的纵坐标是4.
又∵点B的对应点F是直线y=x上的一点,
∴4=x,解得x=7.
∴点F的坐标是(7,4),
∴BF=5.
∴根据平移的性质知AD=BF=5,
∴点A的对应点D点的坐标为(5,6).
故答案为:(5,6).
18.已知:有理数a≠1,我们把称为a的差倒数.例如:2的差倒数是=﹣1,﹣1的差倒数是.如果a1=,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,那么a1 a2…a2022= 1 .
【分析】通过计算可得规律:每3次运算结果循环一次,并且a1 a2 a3=﹣1,即可求解.
解:∵a1=,
∴a2==,
a3==﹣2,
a4==,
…,
∴每3次运算结果循环一次,
∵a1=,a2=,a3=﹣2,
∴a1 a2 a3=﹣1,
∵2022÷3=674,
∴a1 a2…a2022=1,
故答案为:1.
三、解答题(本大题共9小题,共78分,解答要写出必要的文字说明、证明过程或推演步骤)
19.解方程:+=4.
【分析】将分式方程转化为整式方程,然后解方程,注意分式方程的结果要进行检验.
解:给分式方程两边同时乘以2x﹣3,
得x﹣5=4(2x﹣3),
解得x=1,
检验:把x=1代入2x﹣3≠0,
所以x=1是原分式方程的解.
20.先化简再求值:(﹣1)÷,其中a=1.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将a的值代入计算即可.
解:原式=(﹣)÷
=
=,
当a=1时,
原式==1.
21.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
【分析】由平行四边形的性质得AD∥BC,AD=BC,则∠ODF=∠OBE,再证△DOF≌△BOE(ASA),得DF=BE,则AF=EC,即可得出结论.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODF=∠OBE,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(ASA),
∴DF=BE,
∴AD﹣DF=BC﹣BE,
即AF=EC,
∴四边形AECF为平行四边形.
22.已知△OAB在平面直角坐标系中的位置如图所示,请解答以下问题:
(1)按要求作图:
先将△OAB绕原点O逆时针旋转90°,得到△OA1B1,再作出△OA2B2,使它与△OA1B1关于原点成中心对称;
(2)直接写出点A1的坐标 (﹣1,3) ;点B2的坐标 (2,﹣2) .
【分析】(1)根据旋转的性质先将△OAB绕原点O逆时针旋转90°,得到△OA1B1,再根据对称的性质作出△OA2B2,使它与△OA1B1关于原点成中心对称;
(2)结合(1)即可写出点A1的坐标;点B2的坐标.
解:(1)如图,△OA1B1,△OA2B2即为所求;
(2)点A1的坐标(﹣1,3);点B2的坐标(2,﹣2).
故答案为:(﹣1,3);(2,﹣2).
23.2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:
抽取七年级教师的竞赛成绩(单位:分)
6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10.
七、八年级教师竞赛成绩统计表
年级 七年级 八年级
平均数 8.5 8.5
中位数 8 a
众数 8 9
优秀率 b 55%
根据以上信息,解答下列问题:
(1)填空:a= 9 ,b= 45% ;
(2)估计该校七年级80名教师中竞赛成绩达到8分及以上的人数;
(3)根据以上数据分析,评价两个年级教师学习党史的竞赛成绩谁更优异.
【分析】(1)根据中位数定义、众数的定义即可找到a、b的值.
(2)计算出成绩达到8分及以上的人数的频率即可求解.
(3)根据优秀率进行评价即可.
解:(1)∵八年级教师竞赛成绩中9分以下的占:5%+10%+30%=45%,
故从小到大排列第10、11个数均为9,
∴a=9,
b==45%;
故答案为:9;45%;
(2)该校七年级80名教师中竞赛成绩达到8分及以上的人数为:80×=68(人);
(3)根据表中可得,七八年级的平均数一样,但八年级的中位数、众数,优秀均高于七年级,因此八年级的教师学习党史的竞赛成绩更优异.
24.如图,已知△ABC中,AB=AC,将△ABC绕点A沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=1,∠BAC=45°,当四边形ADFC是平行四边形时,求EC的长.
【分析】(1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS得到三角形AEC与三角形ADB全等即可;
(2)根据∠BAC=45°,四边形ADFC是平行四边形,得到∠DBA=∠BAC=45°,再由AB=AD,得到三角形ABD为直角三角形,由勾股定理求出BD的长即可.
【解答】(1)证明:由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS);
(2)解:∵四边形ADFC是平行四边形,
∴AC∥DF,
∴∠ABD=∠BAC=45°,
又∵AD=AB,
∴∠ADB=∠ABD=45°
∴∠DAB=90°,
由勾股定理得BD=,
∵△AEC≌△ADB,
∴EC=DB=.
25.某生态示范园积极响应政府提出的“践行生态有机理念,推动有机农业发展”经济政策,培育优良品种,种植了多种有机水果.某超市从该示范园第一次用300元购进甲种水果,300元购进乙种水果.乙种水果的进价是甲种水果进价的1.5倍,超市所进甲种水果比所进乙种水果多10kg.
(1)求甲、乙两种水果的进价分别是每千克多少元?
(2)第一次购进的水果很快销售完毕,为满足消费者需求,该超市准备再次购进甲,乙两种有机水果共100千克,其中甲种水果的质量不少于乙种水果质量的3倍.若甲种水果的售价为13元/千克,乙种水果的售价为20元/千克,超市购进两种有机水果各多少千克时第二次获得最大利润,最大利润是多少?
【分析】(1)根据题意,先设出甲、乙两种水果的单价,然后根据超市所进甲种水果比所进乙种水果多10kg,可以列出相应的分式方程,然后求解即可,注意分式方程要检验;
(2)根据题意,可以写出利润和购买甲种水果数量的函数关系式,然后根据甲种水果的质量不少于乙种水果质量的3倍,可以得到甲种水果数量的取值范围,再根据一次函数的性质,即可得到利润的最大值.
解:(1)设甲种水果的进价是x元/千克,则乙种水果的进价为1.5x元/千克,
﹣=10,
解得x=10,
经检验:x=10是原分式方程的解,
∴1.5x=15,
答:甲种水果的进价是10元/千克,乙种水果的进价为15元/千克;
(2)设购进甲种水果a千克,则购进乙种水果(100﹣a)千克,利润为w元,
由题意可得:w=(13﹣10)a+(20﹣15)(100﹣a)=﹣2a+500,
∴w随a的增大而减小,
∵甲种水果的质量不少于乙种水果质量的3倍,
∴a≥3(100﹣a),
解得a≥75,
∴当a=75时,w取得最大值,此时w=350,100﹣a=25,
答:超市购进甲种水果75千克,乙种水果25千克时第二次获得最大利润,最大利润是350元.
26.点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
【分析】(1)利用三角形的中位线可得AB∥MF,AB=MF,结合平行四边形的性质可得MF∥CD,MF=CD,进而可证明结论;
(2)连接AF,BF,则AF是△MNE的中位线,证明四边形AFBE是平行四边形,再利用平行四边形的性质可求解.
【解答】(1)证明:∵AE=AM,EB=BN,
∴AB为△EMN的中位线,
∴AB∥MN,AB=MN,
∵MF=MN,
∴AB∥MF,AB=MF,
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴MF∥CD,MF=CD,
∴四边形MFCD为平行四边形;
(2)解:连接AF,BF,则AF是△MNE的中位线,
∴AF∥EB,AF=EB,
∴四边形AFBE是平行四边形,
∴OF=OE=2,
∴EF=4.
27.(1)如图1,△ABC和△AMN都是等腰直角三角形,直角顶点为点A,△ABC固定不动,△AMN可以绕着点A旋转.
①如图2,将△AMN绕点A旋转,使点M落在BC边上,连接CN.
直接写出图中的全等三角形: △BAM≌△CAN ;直接写出线段CN,CM,CB之间满足的等量关系为: CN+CM=CB ;
②如图2,试探索线段MA,MB,MC之间满足的等量关系,并完整地证明你的结论;
(2)如图3,P是等腰直角△ABC内一点,∠BAC=90°,连接PA,PB,PC,将△BAP绕点A顺时针旋转90°后得到△CAQ,连接PQ.已知PA=2,PB=3,若∠PQC=90°,求PC的长.
【分析】(1)①根据SAS可证△BAM≌△CAN,得出BM=CN,即可得出CN+CM=CB;
②同理证△BAM≌△CAN,得出∠ACN=∠B=45°,即∠BCN=90°,根据勾股定理即可得出CN2+MC2=MN2,进而得出MB2+MC2=2MA2;
(2)由旋转知△BAP≌△CAQ,得出△PAQ是等腰直角三角形,推出PC2=PA2+QA2,即可得出PC.
解:(1)①∵∠BAM+∠MAC=90°,∠CAN+∠MAC=90°,
∴∠BAM=∠CAN,
在△BAM和△CAN中:
,
∴△BAM≌△CAN(SAS),
∴BM=CN,
∵BM+CM=CB,
∴CN+CM=CB,
故答案为:△BAM≌△CAN,CN+CM=CB;
②MB2+MC2=2MA2;证明如下:
同理①可证△BAM≌△CAN,
∴∠ACN=∠B=45°,
即∠BCN=90°,
∴CN2+MC2=MN2,
在R△MAN中,MN2=MA2+AN2=2MA2,
∴MB2+MC2=2MA2;
(2)由旋转知△BAP≌△CAQ,
∴PA=QA=2,∠PAQ=∠BAC=90°,CQ=BP=3,
∴△PAQ为等腰直角三角形,
∴PQ2=PA2+QA2=22+22=8,
∵∠PQC=90°,
∴PC2=PQ2+QC2=8+32=17,
∴PC=.
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂写在答题卡上,每小题选对得4分,选错、不选或选出的答案超过一个均记0分,共48分)
1.分解因式4x2﹣y2的结果是( )
A.(4x+y)(4x﹣y) B.4(x+y)(x﹣y)
C.(2x+y)(2x﹣y) D.2(x+y)(x﹣y)
2.下列分式中是最简分式的是( )
A. B.
C. D.
3.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数(单位:分)及方差s2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
甲 乙 丙 丁
6 7 7 6
s2 1 1.1 1 1.6
A.甲 B.乙 C.丙 D.丁
4.京剧脸谱、剪纸等图案蕴含着简洁美对称美,下面选取的图片中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
5.在对一组样本数据进行分析时,小月列出了方差的计算公式:s2=,由公式提供的信息,则下列说法错误的是( )
A.样本的众数是3 B.样本的中位数是2.5
C.样本的平均数是3 D.n=4
6.如果一个多边形的内角和是它的外角和的5倍,则这个多边形是( )
A.十边形 B.十一边形 C.十二边形 D.十三边形
7.如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,将△ABC平移后得到△A'B'C',顶点C平移到了点C'(2,1),则点B的对应点B'的坐标为( )
A.(﹣1,0) B.(1,3) C.(﹣2,0) D.(0,1)
8.关于x的分式方程+5=有增根,则m的值为( )
A.5 B.4 C.3 D.1
9.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,∠ACB=22°,则∠ADC=( )
A.57° B.62° C.67° D.72°
10. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
11.某班学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了15分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的平均速度是骑车同学速度的3倍,设骑车同学的平均速度是x千米/小时,则下列方程正确的是( )
A. B.
C. D.
12.在 ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①GN=NE;②AE⊥GF;③AC平分∠BCD;④AC⊥BD,其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题填对得4分,共24分。请填在答题卡上)
13.分解因式:a3﹣2a2+a= .
14.化简的结果是 .
15.“阳光小区”开展“节约用水,从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较,统计出节水情况如表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 3 2 3 1 1
那么这10个家庭的节水量(m3)的平均数是 .
16.如图,已知 ABCD的周长为38,对角线AC、BD相交于点O,点E是CD的中点,△DOE的周长为16,则BD的长为 .
17.在平面直角坐标系中,点A的坐标为(0,6)点B的坐标为(2,4),△OAB沿x轴向右平移后得到△EDF,点B的对应点F是直线y=x上的一点,则点A的对应点D点的坐标为 .
18.已知:有理数a≠1,我们把称为a的差倒数.例如:2的差倒数是=﹣1,﹣1的差倒数是.如果a1=,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,那么a1 a2…a2022= .
三、解答题(本大题共9小题,共78分,解答要写出必要的文字说明、证明过程或推演步骤)
19.解方程:+=4.
20.先化简再求值:(﹣1)÷,其中a=1.
21.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
22.已知△OAB在平面直角坐标系中的位置如图所示,请解答以下问题:
(1)按要求作图:
先将△OAB绕原点O逆时针旋转90°,得到△OA1B1,再作出△OA2B2,使它与△OA1B1关于原点成中心对称;
(2)直接写出点A1的坐标 ;点B2的坐标 .
23.2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:
抽取七年级教师的竞赛成绩(单位:分)
6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10.
七、八年级教师竞赛成绩统计表
年级 七年级 八年级
平均数 8.5 8.5
中位数 8 a
众数 8 9
优秀率 b 55%
根据以上信息,解答下列问题:
(1)填空:a= ,b= ;
(2)估计该校七年级80名教师中竞赛成绩达到8分及以上的人数;
(3)根据以上数据分析,评价两个年级教师学习党史的竞赛成绩谁更优异.
24.如图,已知△ABC中,AB=AC,将△ABC绕点A沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=1,∠BAC=45°,当四边形ADFC是平行四边形时,求EC的长.
25.某生态示范园积极响应政府提出的“践行生态有机理念,推动有机农业发展”经济政策,培育优良品种,种植了多种有机水果.某超市从该示范园第一次用300元购进甲种水果,300元购进乙种水果.乙种水果的进价是甲种水果进价的1.5倍,超市所进甲种水果比所进乙种水果多10kg.
(1)求甲、乙两种水果的进价分别是每千克多少元?
(2)第一次购进的水果很快销售完毕,为满足消费者需求,该超市准备再次购进甲,乙两种有机水果共100千克,其中甲种水果的质量不少于乙种水果质量的3倍.若甲种水果的售价为13元/千克,乙种水果的售价为20元/千克,超市购进两种有机水果各多少千克时第二次获得最大利润,最大利润是多少?
26.点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
27.(1)如图1,△ABC和△AMN都是等腰直角三角形,直角顶点为点A,△ABC固定不动,△AMN可以绕着点A旋转.
①如图2,将△AMN绕点A旋转,使点M落在BC边上,连接CN.
直接写出图中的全等三角形: ;直接写出线段CN,CM,CB之间满足的等量关系为: ;
②如图2,试探索线段MA,MB,MC之间满足的等量关系,并完整地证明你的结论;
(2)如图3,P是等腰直角△ABC内一点,∠BAC=90°,连接PA,PB,PC,将△BAP绕点A顺时针旋转90°后得到△CAQ,连接PQ.已知PA=2,PB=3,若∠PQC=90°,求PC的长.
参考答案
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确选项的代码涂写在答题卡上,每小题选对得4分,选错、不选或选出的答案超过一个均记0分,共48分)
1.分解因式4x2﹣y2的结果是( )
A.(4x+y)(4x﹣y) B.4(x+y)(x﹣y)
C.(2x+y)(2x﹣y) D.2(x+y)(x﹣y)
【分析】直接利用平方差公式分解因式得出答案.
解:4x2﹣y2=(2x+y)(2x﹣y).
故选:C.
2.下列分式中是最简分式的是( )
A. B.
C. D.
【分析】利用最简分式定义:分子分母没有公因式的分式,判断即可.
解:A.该分式符合最简分式的定义,符合题意;
B.该分式的分子、分母中含有公因式(x﹣1),不是最简分式,不符合题意
C.该分式的分子、分母中含有公因式(x+1),不是最简分式,不符合题意;
D.该分式的分子、分母中含有公因式(x﹣1),不是最简分式,不符合题意;
故选:A.
3.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数(单位:分)及方差s2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
甲 乙 丙 丁
6 7 7 6
s2 1 1.1 1 1.6
A.甲 B.乙 C.丙 D.丁
【分析】先比较平均数得到乙组和丙组成绩较好,然后比较方差得到丙组的状态稳定,于是可决定选丙组去参赛.
解:因为乙组、丙组的平均数比甲组、丁组大,而丙组的方差比乙组的小,
所以丙组的成绩比较稳定,
所以丙组的成绩较好且状态稳定,应选的组是丙组.
故选:C.
4.京剧脸谱、剪纸等图案蕴含着简洁美对称美,下面选取的图片中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.是轴对称图形,不是中心对称图形,故本选项不合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.不是轴对称图形,是中心对称图形,故本选项不合题意;
D.既是轴对称图形又是中心对称图形,故本选项符合题意.
故选:D.
5.在对一组样本数据进行分析时,小月列出了方差的计算公式:s2=,由公式提供的信息,则下列说法错误的是( )
A.样本的众数是3 B.样本的中位数是2.5
C.样本的平均数是3 D.n=4
【分析】根据方差的计算公式得出数据为2、3、3、4,再利用众数、中位数、平均数的定义求解即可.
解:由题意知,这组数据2、3、3、4,
所以样本的众数是3,中位数是=3,平均数为=3,n=4,
故选:B.
6.如果一个多边形的内角和是它的外角和的5倍,则这个多边形是( )
A.十边形 B.十一边形 C.十二边形 D.十三边形
【分析】根据多边形的内角和公式、外角和公式,可得方程,根据解方程,可得答案.
解:设这个多边形是n边形,由题意,得
(n﹣2)×180°=5×360°.
解得n=12,
故选:C.
7.如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,将△ABC平移后得到△A'B'C',顶点C平移到了点C'(2,1),则点B的对应点B'的坐标为( )
A.(﹣1,0) B.(1,3) C.(﹣2,0) D.(0,1)
【分析】根据上下平移横坐标不变,纵坐标上加下减,可得结论.
解:∵顶点C(0,2)平移到了点C'(2,1),
∴,△ABC向右平移了2﹣2=2个单位,向下平移了2﹣1=1个单位,
∴点B(﹣3,1)向右平移2个单位,向下平移1个单位,
得到B'(﹣1,0),
故选:A.
8.关于x的分式方程+5=有增根,则m的值为( )
A.5 B.4 C.3 D.1
【分析】根据分式方程的解法即可求出答案.
解:7x+5(x﹣1)=2m﹣1
x=
由题意可知:x=代入x﹣1=0,
﹣1=0
解得:m=4
故选:B.
9.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,∠ACB=22°,则∠ADC=( )
A.57° B.62° C.67° D.72°
【分析】由旋转的性质可得CA=CE,∠ACE=90°,∠ACB=∠DCE=22°,从而得△ACE是等腰直角三角形,进而得∠E=45°,最后利用∠ADC是△CDE的外角即可解答.
解:由旋转可得:
∠ACB=∠DCE=22°,CA=CE,∠ACE=90°,
∴△ACE是等腰直角三角形,
∴∠E=45°,
∵∠ADC是△CDE的一个外角,
∴∠ADC=∠E+∠DCE=45°+22°=67°,
故选:C.
10. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
【分析】连接AC与BD相交于O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,再根据对角线互相平分的四边形是平行四边形,只要证明得到OE=OF即可,然后根据各选项的条件分析判断即可得解.
解:如图,连接AC与BD相交于O,
在 ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
C、若CE=AF,则无法判断OE=OE,故本选项符合题意;
D、由∠DAF=∠BCE,从而推出△DAF≌△BCE,然后得出∠DFA=∠BEC,∴∠AFE=∠CEF,∴AF∥CE,结合选项B可证明四边形AECF是平行四边形;故本选项不符合题意;
故选:C.
11.某班学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了15分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的平均速度是骑车同学速度的3倍,设骑车同学的平均速度是x千米/小时,则下列方程正确的是( )
A. B.
C. D.
【分析】关键描述语:“过了15分钟后,其余同学乘汽车出发,结果他们同时到达”;等量关系为:骑自行车同学所用时间﹣乘车同学所用时间=.
解:设骑车学生的平均速度为xkm/h,则汽车的平均速度为3xkm/h.
根据题意,列方程得.
故选:B.
12.在 ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①GN=NE;②AE⊥GF;③AC平分∠BCD;④AC⊥BD,其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】通过证明四边形BGFE是平行四边形,可得GN=NE,故①正确;由等腰三角形的性质可得BE⊥AC,由平行四边形的性质可证GF⊥AE,故②正确;由外角的性质可得∠BOC>∠ACD,由等腰三角形的性质可得∠BOC=∠BCO≠∠ACD,故③错误;由等腰三角形的性质可得BE⊥AE,可得∠BOE<90°,则AC与BD不垂直,故④错误,即可求解.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E、F、G分别是OC、OD、AB的中点,
∴CD=2EF,EF∥CD,AB=2BG,
∴BG=EF,AB∥EF∥CD,
∴四边形BGFE是平行四边形,
∴GN=NE,故①正确;
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD=BC,
∵BD=2AD=2BC,
∴BO=BC,
又∵点E是OC的中点,
∴BE⊥AC,
∵四边形BGFE是平行四边形,
∴GF∥BE,
∴GF⊥AC,
即GF⊥AE,故②正确;
∵BO=BC,
∴∠BOC=∠BCO,
∵∠BOC=∠ACD+∠BDC,
∴∠BOC>∠ACD,
∴∠BCO≠∠ACD,
∴AC不平分∠BCD,故③错误;
∵BO=BC,点E是OC的中点,
∴BE⊥AC,
∴∠BOE<90°,
∴AC与BD不垂直,故④错误,
故选:B.
二、填空题(本大题共6小题,每小题填对得4分,共24分。请填在答题卡上)
13.分解因式:a3﹣2a2+a= a(a﹣1)2 .
【分析】此多项式有公因式,应先提取公因式a,再对余下的多项式进行观察,有3项,可利用完全平方公式继续分解.
解:a3﹣2a2+a
=a(a2﹣2a+1)
=a(a﹣1)2.
故答案为:a(a﹣1)2.
14.化简的结果是 .
【分析】直接将原式通分,进而利用分式的加减运算法则计算得出答案.
解:原式=+
=
=.
故答案为:.
15.“阳光小区”开展“节约用水,从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较,统计出节水情况如表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 3 2 3 1 1
那么这10个家庭的节水量(m3)的平均数是 0.45 .
【分析】根据加权平均数的计算公式即可求出答案.
解:根据题意得:
(0.3×3+0.4×2+0.5×3+0.6×1+0.7×1)=0.45(m3),
答:这10个家庭的节水量(m3)的平均数是0.45m3.
故答案为:0.45.
16.如图,已知 ABCD的周长为38,对角线AC、BD相交于点O,点E是CD的中点,△DOE的周长为16,则BD的长为 13 .
【分析】根据平行四边形的性质知O为BD的中点,即可判断OE是△DBC的中位线,即OE=BC,从而得出△BCD的周长是△DOE的周长的二倍,再根据BC+CD是平行四边形周长的一半求出BD的长即可.
解:∵四边形ABCD是平行四边形,且周长为38,
∴O是BD的中点,BC+CD=38×=19,
∵点E是CD的中点,
∴OE是△DBC的中位线,
∴△BCD的周长是△DOE的周长的2倍,
即BD+BC+DC=2(OD+OE+ED)=2×16,
∴BD+19=32,
解得:BD=13,
故答案为:13.
17.在平面直角坐标系中,点A的坐标为(0,6)点B的坐标为(2,4),△OAB沿x轴向右平移后得到△EDF,点B的对应点F是直线y=x上的一点,则点A的对应点D点的坐标为 (5,6) .
【分析】根据平移的性质知BF=AD.由一次函数图象上点的坐标特征可以求得点F的坐标,所以根据两点间的距离公式可以求得线段BF的长度,即AD的长度.
解:∵点A的坐标为(0,6)点B的坐标为(2,4),△OAB沿x轴向右平移后得到△EDF,
∴点D的纵坐标是6,点F的纵坐标是4.
又∵点B的对应点F是直线y=x上的一点,
∴4=x,解得x=7.
∴点F的坐标是(7,4),
∴BF=5.
∴根据平移的性质知AD=BF=5,
∴点A的对应点D点的坐标为(5,6).
故答案为:(5,6).
18.已知:有理数a≠1,我们把称为a的差倒数.例如:2的差倒数是=﹣1,﹣1的差倒数是.如果a1=,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,那么a1 a2…a2022= 1 .
【分析】通过计算可得规律:每3次运算结果循环一次,并且a1 a2 a3=﹣1,即可求解.
解:∵a1=,
∴a2==,
a3==﹣2,
a4==,
…,
∴每3次运算结果循环一次,
∵a1=,a2=,a3=﹣2,
∴a1 a2 a3=﹣1,
∵2022÷3=674,
∴a1 a2…a2022=1,
故答案为:1.
三、解答题(本大题共9小题,共78分,解答要写出必要的文字说明、证明过程或推演步骤)
19.解方程:+=4.
【分析】将分式方程转化为整式方程,然后解方程,注意分式方程的结果要进行检验.
解:给分式方程两边同时乘以2x﹣3,
得x﹣5=4(2x﹣3),
解得x=1,
检验:把x=1代入2x﹣3≠0,
所以x=1是原分式方程的解.
20.先化简再求值:(﹣1)÷,其中a=1.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将a的值代入计算即可.
解:原式=(﹣)÷
=
=,
当a=1时,
原式==1.
21.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
【分析】由平行四边形的性质得AD∥BC,AD=BC,则∠ODF=∠OBE,再证△DOF≌△BOE(ASA),得DF=BE,则AF=EC,即可得出结论.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODF=∠OBE,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(ASA),
∴DF=BE,
∴AD﹣DF=BC﹣BE,
即AF=EC,
∴四边形AECF为平行四边形.
22.已知△OAB在平面直角坐标系中的位置如图所示,请解答以下问题:
(1)按要求作图:
先将△OAB绕原点O逆时针旋转90°,得到△OA1B1,再作出△OA2B2,使它与△OA1B1关于原点成中心对称;
(2)直接写出点A1的坐标 (﹣1,3) ;点B2的坐标 (2,﹣2) .
【分析】(1)根据旋转的性质先将△OAB绕原点O逆时针旋转90°,得到△OA1B1,再根据对称的性质作出△OA2B2,使它与△OA1B1关于原点成中心对称;
(2)结合(1)即可写出点A1的坐标;点B2的坐标.
解:(1)如图,△OA1B1,△OA2B2即为所求;
(2)点A1的坐标(﹣1,3);点B2的坐标(2,﹣2).
故答案为:(﹣1,3);(2,﹣2).
23.2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:
抽取七年级教师的竞赛成绩(单位:分)
6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10.
七、八年级教师竞赛成绩统计表
年级 七年级 八年级
平均数 8.5 8.5
中位数 8 a
众数 8 9
优秀率 b 55%
根据以上信息,解答下列问题:
(1)填空:a= 9 ,b= 45% ;
(2)估计该校七年级80名教师中竞赛成绩达到8分及以上的人数;
(3)根据以上数据分析,评价两个年级教师学习党史的竞赛成绩谁更优异.
【分析】(1)根据中位数定义、众数的定义即可找到a、b的值.
(2)计算出成绩达到8分及以上的人数的频率即可求解.
(3)根据优秀率进行评价即可.
解:(1)∵八年级教师竞赛成绩中9分以下的占:5%+10%+30%=45%,
故从小到大排列第10、11个数均为9,
∴a=9,
b==45%;
故答案为:9;45%;
(2)该校七年级80名教师中竞赛成绩达到8分及以上的人数为:80×=68(人);
(3)根据表中可得,七八年级的平均数一样,但八年级的中位数、众数,优秀均高于七年级,因此八年级的教师学习党史的竞赛成绩更优异.
24.如图,已知△ABC中,AB=AC,将△ABC绕点A沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=1,∠BAC=45°,当四边形ADFC是平行四边形时,求EC的长.
【分析】(1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS得到三角形AEC与三角形ADB全等即可;
(2)根据∠BAC=45°,四边形ADFC是平行四边形,得到∠DBA=∠BAC=45°,再由AB=AD,得到三角形ABD为直角三角形,由勾股定理求出BD的长即可.
【解答】(1)证明:由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS);
(2)解:∵四边形ADFC是平行四边形,
∴AC∥DF,
∴∠ABD=∠BAC=45°,
又∵AD=AB,
∴∠ADB=∠ABD=45°
∴∠DAB=90°,
由勾股定理得BD=,
∵△AEC≌△ADB,
∴EC=DB=.
25.某生态示范园积极响应政府提出的“践行生态有机理念,推动有机农业发展”经济政策,培育优良品种,种植了多种有机水果.某超市从该示范园第一次用300元购进甲种水果,300元购进乙种水果.乙种水果的进价是甲种水果进价的1.5倍,超市所进甲种水果比所进乙种水果多10kg.
(1)求甲、乙两种水果的进价分别是每千克多少元?
(2)第一次购进的水果很快销售完毕,为满足消费者需求,该超市准备再次购进甲,乙两种有机水果共100千克,其中甲种水果的质量不少于乙种水果质量的3倍.若甲种水果的售价为13元/千克,乙种水果的售价为20元/千克,超市购进两种有机水果各多少千克时第二次获得最大利润,最大利润是多少?
【分析】(1)根据题意,先设出甲、乙两种水果的单价,然后根据超市所进甲种水果比所进乙种水果多10kg,可以列出相应的分式方程,然后求解即可,注意分式方程要检验;
(2)根据题意,可以写出利润和购买甲种水果数量的函数关系式,然后根据甲种水果的质量不少于乙种水果质量的3倍,可以得到甲种水果数量的取值范围,再根据一次函数的性质,即可得到利润的最大值.
解:(1)设甲种水果的进价是x元/千克,则乙种水果的进价为1.5x元/千克,
﹣=10,
解得x=10,
经检验:x=10是原分式方程的解,
∴1.5x=15,
答:甲种水果的进价是10元/千克,乙种水果的进价为15元/千克;
(2)设购进甲种水果a千克,则购进乙种水果(100﹣a)千克,利润为w元,
由题意可得:w=(13﹣10)a+(20﹣15)(100﹣a)=﹣2a+500,
∴w随a的增大而减小,
∵甲种水果的质量不少于乙种水果质量的3倍,
∴a≥3(100﹣a),
解得a≥75,
∴当a=75时,w取得最大值,此时w=350,100﹣a=25,
答:超市购进甲种水果75千克,乙种水果25千克时第二次获得最大利润,最大利润是350元.
26.点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
【分析】(1)利用三角形的中位线可得AB∥MF,AB=MF,结合平行四边形的性质可得MF∥CD,MF=CD,进而可证明结论;
(2)连接AF,BF,则AF是△MNE的中位线,证明四边形AFBE是平行四边形,再利用平行四边形的性质可求解.
【解答】(1)证明:∵AE=AM,EB=BN,
∴AB为△EMN的中位线,
∴AB∥MN,AB=MN,
∵MF=MN,
∴AB∥MF,AB=MF,
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴MF∥CD,MF=CD,
∴四边形MFCD为平行四边形;
(2)解:连接AF,BF,则AF是△MNE的中位线,
∴AF∥EB,AF=EB,
∴四边形AFBE是平行四边形,
∴OF=OE=2,
∴EF=4.
27.(1)如图1,△ABC和△AMN都是等腰直角三角形,直角顶点为点A,△ABC固定不动,△AMN可以绕着点A旋转.
①如图2,将△AMN绕点A旋转,使点M落在BC边上,连接CN.
直接写出图中的全等三角形: △BAM≌△CAN ;直接写出线段CN,CM,CB之间满足的等量关系为: CN+CM=CB ;
②如图2,试探索线段MA,MB,MC之间满足的等量关系,并完整地证明你的结论;
(2)如图3,P是等腰直角△ABC内一点,∠BAC=90°,连接PA,PB,PC,将△BAP绕点A顺时针旋转90°后得到△CAQ,连接PQ.已知PA=2,PB=3,若∠PQC=90°,求PC的长.
【分析】(1)①根据SAS可证△BAM≌△CAN,得出BM=CN,即可得出CN+CM=CB;
②同理证△BAM≌△CAN,得出∠ACN=∠B=45°,即∠BCN=90°,根据勾股定理即可得出CN2+MC2=MN2,进而得出MB2+MC2=2MA2;
(2)由旋转知△BAP≌△CAQ,得出△PAQ是等腰直角三角形,推出PC2=PA2+QA2,即可得出PC.
解:(1)①∵∠BAM+∠MAC=90°,∠CAN+∠MAC=90°,
∴∠BAM=∠CAN,
在△BAM和△CAN中:
,
∴△BAM≌△CAN(SAS),
∴BM=CN,
∵BM+CM=CB,
∴CN+CM=CB,
故答案为:△BAM≌△CAN,CN+CM=CB;
②MB2+MC2=2MA2;证明如下:
同理①可证△BAM≌△CAN,
∴∠ACN=∠B=45°,
即∠BCN=90°,
∴CN2+MC2=MN2,
在R△MAN中,MN2=MA2+AN2=2MA2,
∴MB2+MC2=2MA2;
(2)由旋转知△BAP≌△CAQ,
∴PA=QA=2,∠PAQ=∠BAC=90°,CQ=BP=3,
∴△PAQ为等腰直角三角形,
∴PQ2=PA2+QA2=22+22=8,
∵∠PQC=90°,
∴PC2=PQ2+QC2=8+32=17,
∴PC=.
同课章节目录
