2021-2022学年人教版九年级下 28.2解直角三角形及其应用同步练习(含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级下 28.2解直角三角形及其应用同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 10:52:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级下 28.2解直角三角形及其应用同步练习
一.选择题
1.(2021秋 泗水县期末)如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cosB的是( )
A. B. C. D.
2.(2021秋 市北区期末)在Rt△ABC中,∠C=90°,已知∠A及边BC=a,则Rt△ABC的斜边长应为( )
A.asinA B. C.acosA D.
3.(2021秋 嘉定区期末)在△ABC中,AB=AC=10,,那么BC的长是( )
A.4 B.8 C. D.
4.(2021秋 拱墅区期末)如图,在平面直角坐标系内有一点P(3,4),连接OP,设OP与x轴正半轴所夹的锐角为α,则锐角α的正弦值为( )
A. B. C. D.
5.(2021秋 海口期末)一段拦水坝横断面如图所示,迎水坡AB的坡度为i=1:,坝高BC=6m,则坡面AB的长度( )
A.12m B.18m C.6 D.12
6.(2021秋 青岛期末)如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC=( )
A. B. C. D.
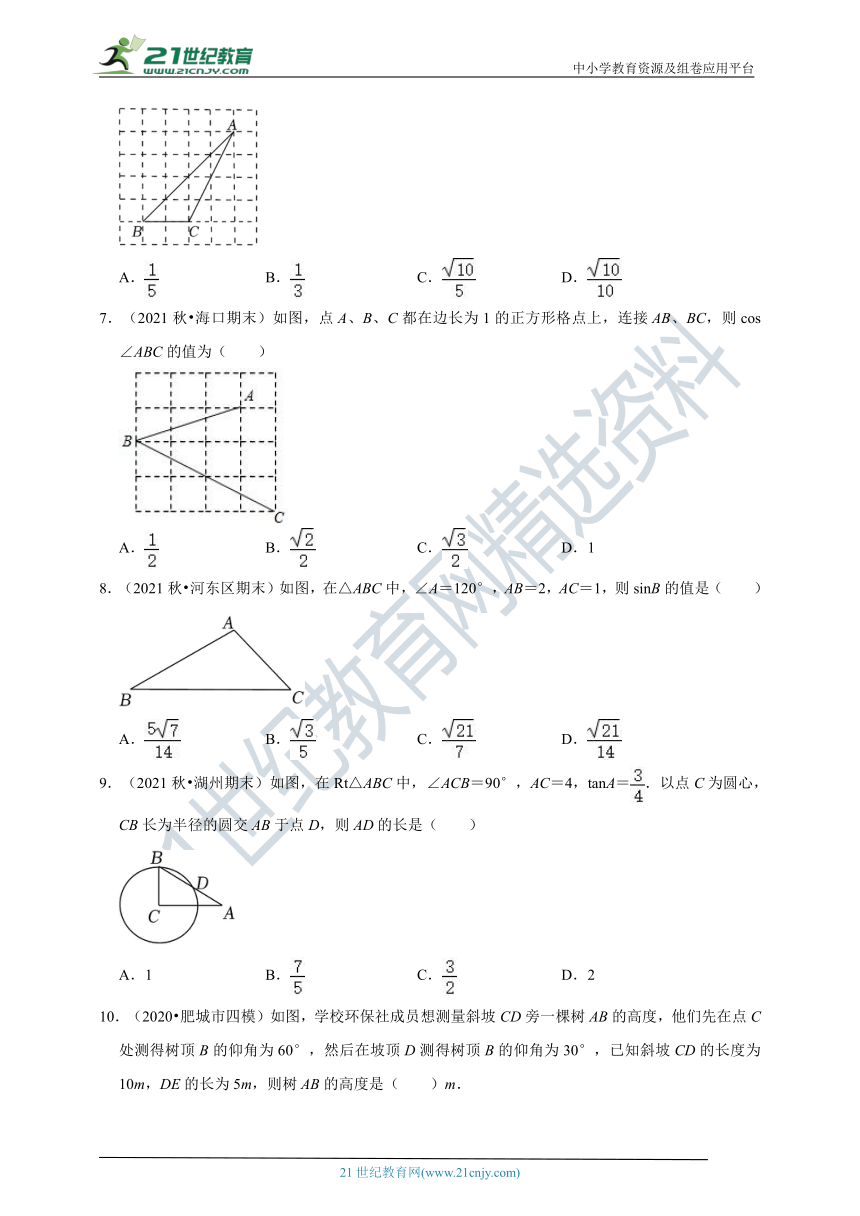
7.(2021秋 海口期末)如图,点A、B、C都在边长为1的正方形格点上,连接AB、BC,则cos∠ABC的值为( )
A. B. C. D.1
8.(2021秋 河东区期末)如图,在△ABC中,∠A=120°,AB=2,AC=1,则sinB的值是( )
A. B. C. D.
9.(2021秋 湖州期末)如图,在Rt△ABC中,∠ACB=90°,AC=4,tanA=.以点C为圆心,CB长为半径的圆交AB于点D,则AD的长是( )
A.1 B. C. D.2
10.(2020 肥城市四模)如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10 B.15 C.15 D.15﹣5
二.填空题
11.(2021秋 长春期末)如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,则sinB的值为 .
12.(2021秋 杨浦区期末)如图,海中有一个小岛A,一艘轮船由西向东航行,在点B处测得小岛A在它的北偏东60°方向上,航行12海里到达点C处,测得小岛A在它的北偏东30°方向上,那么小岛A到航线BC的距离等于 海里.
13.(2021秋 普陀区期末)如图,在△ABC中,∠A=90°,斜边BC的垂直平分线分别交AB、BC交于点D、E,如果cosB=,AB=7,那么CD的长等于 .
14.(2021秋 邵东市期末)如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向(点A、B、C在同一平面),则这段河的宽度为 米(结果保留根号)
15.(2021秋 潜山市期末)如图,△ABC中,过点B作BD⊥AB,交AC于点D,且AD:CD=4:3,∠ABC=150°.
(1)BD:BC= ;
(2)若AB=4,则△ABC的面积是 .
16.(2021秋 海陵区期末)如图所示,在边长相同的小正方形组成的网格中,两条经过格点的线段相交所成的锐角为α,则cosα等于 .
三.解答题
17.(2021秋 溧阳市期末)(1)在△ABC中,∠C=90°,∠A=60°,BC=8,求AB和AC的长;
(2)在△ABC中,∠C=90°,a=,b=3,解这个直角三角形.
18.(2021秋 青浦区期末)如图,在△ABC中,点D是BC的中点,联结AD,AB=AD,BD=4,tanC=.
(1)求AB的长;
(2)求点C到直线AB的距离.
19.(2021秋 兴宁市期末)如图,某数学兴趣小组为测量一座古塔的高度,在古塔左侧的A点处测得古塔顶端D的仰角为30°,然后向古塔底端C前进30米到达点B处,测得古塔顶端D的仰角为45°,且点A、B、C在同一水平直线上,求古塔CD的高度.
20.(2021秋 房山区期末)如图,在△ABC中,AB=4,∠B=45°,∠C=60°.点E为线段AB的中点,点F是AC边上任一点,作点A关于线段EF的对称点P,连接AP,交EF于点M.连接EP,FP.当PF⊥AC时,求AP的长.
21.(2021秋 永定区期末)如图,一艘船正以海里/小时的速度向正东航行,在A处看小岛C在船北偏东60°,继续航行1小时到达B处,此时看见小岛C在船的北偏东30°.
(1)求小岛C到航线AB的距离.
(2)已知以小岛C为中心周围20海里内为我军导弹部队军事演习的着弹危险区,问这艘船继续向东航行,是否有进入危险区的可能?
22.(2021秋 龙口市期末)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
23.(2021秋 西湖区校级月考)阅读下列材料,并解决问题.
如图1,在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c,过点A作AD⊥BC于点D,则,,即AD=csinB,AD=bsinC.于是csinB=bsinC,即.同理有:,,所以.即在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
(1)如图2,一货轮在B处测得灯塔A在货轮的北偏东15°的方向上,随后货轮以80海里/时的速度向正东方向航行,半小时后到达C处,此时又测得灯塔A在货轮的北偏西30°的方向上,求此时货轮距灯塔A的距离AC.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)
答案与解析
一.选择题
1.(2021秋 泗水县期末)如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cosB的是( )
A. B. C. D.
【解析】解:A.∵CD⊥AB,
∴∠CDB=∠ADB=90°,
∴∠B+∠BCD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠B=∠ACD,
在Rt△ACD中,cos∠ACD=,
∴cosB=,
故A不符合题意;
B.在Rt△DBC中,cosB=,故B不符合题意;
C.在Rt△DBC中,cos∠BCD=,
∵∠A≠45°,
∴∠B≠45°,
∴∠B≠∠BCD,
∴cosB≠,
故C符合题意;
D.在Rt△ABC中,cosB=,故D不符合题意;
故选:C.
2.(2021秋 市北区期末)在Rt△ABC中,∠C=90°,已知∠A及边BC=a,则Rt△ABC的斜边长应为( )
A.asinA B. C.acosA D.
【解析】解:在Rt△ABC中,∠C=90°,已知∠A及边BC=a,
∴AB==,
∴Rt△ABC的斜边长应为:,
故选:B.
3.(2021秋 嘉定区期末)在△ABC中,AB=AC=10,,那么BC的长是( )
A.4 B.8 C. D.
【解析】解:过点A作AD⊥BC,垂足为D,
在Rt△ABD中,AB=10,,
∴BD=ABcosB=10×=4,
∵AB=AC,AD⊥BC,
∴BC=2BD=8,
故选:B.
4.(2021秋 拱墅区期末)如图,在平面直角坐标系内有一点P(3,4),连接OP,设OP与x轴正半轴所夹的锐角为α,则锐角α的正弦值为( )
A. B. C. D.
【解析】解:过点P作PA⊥x轴,垂足为A,
∵P(3,4),
∴OA=3,AP=4,
∴OP===5,
在Rt△OAP中,sinα==,
故选:B.
5.(2021秋 海口期末)一段拦水坝横断面如图所示,迎水坡AB的坡度为i=1:,坝高BC=6m,则坡面AB的长度( )
A.12m B.18m C.6 D.12
【解析】解:∵迎水坡AB的坡度为i=1:,坝高BC=6m,
∴
即
解得AC=6,
∴AB==m,
故选:A.
6.(2021秋 青岛期末)如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC=( )
A. B. C. D.
【解析】解:连接CD,
由图可得:CD⊥AB,
由题意得:CD==,
AC==2,
在Rt△ACD中,sin∠BAC===,
故选:D.
7.(2021秋 海口期末)如图,点A、B、C都在边长为1的正方形格点上,连接AB、BC,则cos∠ABC的值为( )
A. B. C. D.1
【解析】解:连接AC,
由题意得:
AB2=32+12=10,
AC2=12+32=10,
BC2=22+42=20,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,
∵AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∴cos∠ABC=,
故选:B.
8.(2021秋 河东区期末)如图,在△ABC中,∠A=120°,AB=2,AC=1,则sinB的值是( )
A. B. C. D.
【解析】解:过点C作CD⊥BA,交BA的延长线于点D,
∵∠BAC=120°,
∴∠CAD=180°﹣∠BAC=60°,
在Rt△CAD中,CD=ACsin60°=1×=,
AD=ACcos60°=1×=,
∵AB=2,
∴BD=AB+AD=2+=,
在Rt△BCD中,BC===,
∴sinB===,
故选:D.
9.(2021秋 湖州期末)如图,在Rt△ABC中,∠ACB=90°,AC=4,tanA=.以点C为圆心,CB长为半径的圆交AB于点D,则AD的长是( )
A.1 B. C. D.2
【解析】解:过点C作CE⊥AB,垂足为E,
在Rt△ABC中,∠ACB=90°,AC=4,tanA=,
∴,
∴BC=3,
∴AB===5,
∵△ABC的面积=AB CE=AC BC,
∴5CE=12,
∴CE=,
在Rt△BCE中,CE===,
∵CE⊥BD,
∴BD=2BE=,
∴AD=AB﹣BD=5﹣=,
故选:B.
10.(2020 肥城市四模)如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10 B.15 C.15 D.15﹣5
【解析】解:在Rt△CDE中,
∵CD=10m,DE=5m,
∴sin∠DCE=,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===10(m),
∴AB=BC sin60°=10×=15(m).
故选:B.
二.填空题
11.(2021秋 长春期末)如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,则sinB的值为 .
【解析】解:∵CD=6,tanA=,
∴tanA==,
∴AD=4,
∵AB=12,
∴BD=AB﹣AD=12﹣4=8,
由勾股定理可得BC===10,
∴sinB===,
故答案为:.
12.(2021秋 杨浦区期末)如图,海中有一个小岛A,一艘轮船由西向东航行,在点B处测得小岛A在它的北偏东60°方向上,航行12海里到达点C处,测得小岛A在它的北偏东30°方向上,那么小岛A到航线BC的距离等于 6 海里.
【解析】解:过点A作AE⊥BC交BC的延长线于点E,
由题意得:BC=12海里,∠ABC=90°﹣60°=30°,∠ACE=90°﹣30°=60°,
∴∠BAC=∠ACE﹣∠ABC=30°,
∴∠BAC=∠ABC,
∴AC=BC=12海里,
在Rt△ACE中,sin∠ACE=,
∴AE=AC sin∠ACE=12×=6(海里),
即小岛A到航线BC的距离是6海里,
故答案为:6.
13.(2021秋 普陀区期末)如图,在△ABC中,∠A=90°,斜边BC的垂直平分线分别交AB、BC交于点D、E,如果cosB=,AB=7,那么CD的长等于 .
【解析】解:在△ABC中,∠A=90°,cosB=,AB=7,
∴BC=AB÷cosB=7=8,
∵斜边BC的垂直平分线分别交AB、BC交于点D、E,
∴BE=BC=4,
∴CD=BD=BE÷cosB=4=,
故答案为:.
14.(2021秋 邵东市期末)如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向(点A、B、C在同一平面),则这段河的宽度为 米(结果保留根号)
【解析】解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x=30(+1),
答:这段河的宽约为30(+1)米.
故答案为:30(+1).
15.(2021秋 潜山市期末)如图,△ABC中,过点B作BD⊥AB,交AC于点D,且AD:CD=4:3,∠ABC=150°.
(1)BD:BC= 2:7 ;
(2)若AB=4,则△ABC的面积是 2 .
【解析】解:(1)过点C作CE⊥AB,交AB的延长线于点E,
∵∠ABC=150°,
∴∠CBE=180°﹣∠ABC=30°,
∴设CE为a,则BC为2a,
∵BD⊥AB,CE⊥AB,
∴∠ABD=∠AEC=90°,
∵∠A=∠A,
∴△ABD∽△AEC,
∴=,
∴=,
∴BD=a,
∴==,
故答案为:2:7;
(2)由(1)得:△ABD∽△AEC,
∴=,
∴=,
∴AE=7,
∴BE=AE﹣AB=7﹣4=3,
在Rt△BEC中,CE=BEtan30°=3×=,
∴△ABC的面积=AB CE=×4×=2,
故答案为:2.
16.(2021秋 海陵区期末)如图所示,在边长相同的小正方形组成的网格中,两条经过格点的线段相交所成的锐角为α,则cosα等于 .
【解析】解:如图:设AB与CD相交于点E,过点C作CF∥AB,连接DF,
∵AB∥CF,
∴∠AEC=∠DCF,
由勾股定理得:
DC2=12+32=10,
DF2=12+22=5,
CF2=12+22=5,
∴DF2+CF2=DC2,且CF=DF,
∴△DCF是等腰直角三角形,
∴∠DCF=45°,
∴α=45°,
∴cosα=,
故答案为:.
三.解答题
17.(2021秋 溧阳市期末)(1)在△ABC中,∠C=90°,∠A=60°,BC=8,求AB和AC的长;
(2)在△ABC中,∠C=90°,a=,b=3,解这个直角三角形.
【解析】解:(1)在△ABC中,∠C=90°,∠A=60°,BC=8,
∴AB===,
∴AC=ABcos60°=×=,
答:,;
(2)在△ABC中,∠C=90°,a=,b=3,
∴tanA===,
∴∠A=30°,
∴c=2a=2,
∴∠B=90°﹣∠A=60°,
∴,∠A=30°,∠B=60°.
18.(2021秋 青浦区期末)如图,在△ABC中,点D是BC的中点,联结AD,AB=AD,BD=4,tanC=.
(1)求AB的长;
(2)求点C到直线AB的距离.
【解析】解:(1)∵过点A作AH⊥BD,垂足为点H.
∵AB=AD,
∴BH=HD=BD=2.
∵点D是BC的中点,
∴BD=CD=4.
∴HC=HD+CD=6.
∵=,
∴.
∵
=
=.
(2)过点C作CG⊥BA,交BA的延长线于点G.
∵,
∴.
∴.
∴点C到直线AB的距离为.
19.(2021秋 兴宁市期末)如图,某数学兴趣小组为测量一座古塔的高度,在古塔左侧的A点处测得古塔顶端D的仰角为30°,然后向古塔底端C前进30米到达点B处,测得古塔顶端D的仰角为45°,且点A、B、C在同一水平直线上,求古塔CD的高度.
【解析】解:由题意可知,AB=30,∠C=90°,∠A=30°,∠DBC=45°,
在Rt△BCD中,∠BDC=180°﹣90°﹣∠DBC=45°=∠DBC,
∴BC=CD.
设CD=x米,则BC=x米,AC=(30+x)米,
在Rt△ACD中,
tan30°=.
解得x=15+15,
答:古塔CD的高度为(15+15)米.
20.(2021秋 房山区期末)如图,在△ABC中,AB=4,∠B=45°,∠C=60°.点E为线段AB的中点,点F是AC边上任一点,作点A关于线段EF的对称点P,连接AP,交EF于点M.连接EP,FP.当PF⊥AC时,求AP的长.
【解析】解:如图1中,过点A作AD⊥BC于D.
在Rt△ABD中,AD=AB sin45°=4×=4.
如图2中,AC===,
∵PF⊥AC,
∴∠PFA=90°,
∵沿EF将△AEF折叠得到△PEF.
∴△AEF≌△PEF,
∴∠AFE=∠PFE=45°,AF=PF,
∴∠AFE=∠B,
∵∠EAF=∠CAB,
∴△AEF∽△ACB,
∴=,即=,
∴AF=2,
∴AP=AF=2.
21.(2021秋 永定区期末)如图,一艘船正以海里/小时的速度向正东航行,在A处看小岛C在船北偏东60°,继续航行1小时到达B处,此时看见小岛C在船的北偏东30°.
(1)求小岛C到航线AB的距离.
(2)已知以小岛C为中心周围20海里内为我军导弹部队军事演习的着弹危险区,问这艘船继续向东航行,是否有进入危险区的可能?
【解析】解:(1)作CD⊥AB交AB于点D,
由题意可知:∠CAB=90°﹣60°=30°,∠CBD=90°﹣30°=60°,
∴∠ACB=∠CBD﹣∠CAB=30°,
∴∠CAB=∠ACB,
∴AB=CB=×=,
在Rt△CBD中,CD=CB×sin∠CBD=×=16,
∴小岛C到航线AB的距离为16海里;
(2)∵CD=16<20,
∴这艘船继续向东航行会有进入危险区的可能.
22.(2021秋 龙口市期末)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
【解析】解:(1)在Rt△ABE中,AB=26,i==,
设BE=12k,AE=5k,则AB=13k=26,k=2,
∴AE=10(米),BE=24(米);
(2)过点F作FG⊥AD于点G,
由题意可知:FG=BE=24,∠FAD=53°,
在Rt△AFG中,cot53°==0.75,
∴AG=18(米),
∴BF=GE=AG﹣AE=8(米),
答:改造前坡顶与地面的距离BE为24米;BF至少是8米.
23.(2021秋 西湖区校级月考)阅读下列材料,并解决问题.
如图1,在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c,过点A作AD⊥BC于点D,则,,即AD=csinB,AD=bsinC.于是csinB=bsinC,即.同理有:,,所以.即在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
(1)如图2,一货轮在B处测得灯塔A在货轮的北偏东15°的方向上,随后货轮以80海里/时的速度向正东方向航行,半小时后到达C处,此时又测得灯塔A在货轮的北偏西30°的方向上,求此时货轮距灯塔A的距离AC.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)
【解析】解:(1)由示意图可知:∠ACB=60°,
由平行线的性质可知∠ABC=180°﹣30°﹣60°﹣15°=75°,
则∠A=180°﹣∠C﹣∠B=45°,BC=80×=40(海里),
过B作BD⊥AC于点D,
则∠BDC=90°,∠DBC=30°,
∴DC=BC=20(海里),
由勾股定理得:BD==20(海里),
∵∠A=45°,∠ADB=90°,
∴∠ABD=∠A=45°,
∴AD=BD=20海里,
∴AC=AD+CD=(20+20)(海里),
答:此时货轮距灯塔A的距离AC为(20+20)海里;
(2)如图,由(1)知,CD=20海里,BD==20海里,AD=BD=20海里,
∴AC=AD+CD=(20+20)海里,
∵=,
∴=,
∴sin75°=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下 28.2解直角三角形及其应用同步练习
一.选择题
1.(2021秋 泗水县期末)如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cosB的是( )
A. B. C. D.
2.(2021秋 市北区期末)在Rt△ABC中,∠C=90°,已知∠A及边BC=a,则Rt△ABC的斜边长应为( )
A.asinA B. C.acosA D.
3.(2021秋 嘉定区期末)在△ABC中,AB=AC=10,,那么BC的长是( )
A.4 B.8 C. D.
4.(2021秋 拱墅区期末)如图,在平面直角坐标系内有一点P(3,4),连接OP,设OP与x轴正半轴所夹的锐角为α,则锐角α的正弦值为( )
A. B. C. D.
5.(2021秋 海口期末)一段拦水坝横断面如图所示,迎水坡AB的坡度为i=1:,坝高BC=6m,则坡面AB的长度( )
A.12m B.18m C.6 D.12
6.(2021秋 青岛期末)如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC=( )
A. B. C. D.
7.(2021秋 海口期末)如图,点A、B、C都在边长为1的正方形格点上,连接AB、BC,则cos∠ABC的值为( )
A. B. C. D.1
8.(2021秋 河东区期末)如图,在△ABC中,∠A=120°,AB=2,AC=1,则sinB的值是( )
A. B. C. D.
9.(2021秋 湖州期末)如图,在Rt△ABC中,∠ACB=90°,AC=4,tanA=.以点C为圆心,CB长为半径的圆交AB于点D,则AD的长是( )
A.1 B. C. D.2
10.(2020 肥城市四模)如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10 B.15 C.15 D.15﹣5
二.填空题
11.(2021秋 长春期末)如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,则sinB的值为 .
12.(2021秋 杨浦区期末)如图,海中有一个小岛A,一艘轮船由西向东航行,在点B处测得小岛A在它的北偏东60°方向上,航行12海里到达点C处,测得小岛A在它的北偏东30°方向上,那么小岛A到航线BC的距离等于 海里.
13.(2021秋 普陀区期末)如图,在△ABC中,∠A=90°,斜边BC的垂直平分线分别交AB、BC交于点D、E,如果cosB=,AB=7,那么CD的长等于 .
14.(2021秋 邵东市期末)如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向(点A、B、C在同一平面),则这段河的宽度为 米(结果保留根号)
15.(2021秋 潜山市期末)如图,△ABC中,过点B作BD⊥AB,交AC于点D,且AD:CD=4:3,∠ABC=150°.
(1)BD:BC= ;
(2)若AB=4,则△ABC的面积是 .
16.(2021秋 海陵区期末)如图所示,在边长相同的小正方形组成的网格中,两条经过格点的线段相交所成的锐角为α,则cosα等于 .
三.解答题
17.(2021秋 溧阳市期末)(1)在△ABC中,∠C=90°,∠A=60°,BC=8,求AB和AC的长;
(2)在△ABC中,∠C=90°,a=,b=3,解这个直角三角形.
18.(2021秋 青浦区期末)如图,在△ABC中,点D是BC的中点,联结AD,AB=AD,BD=4,tanC=.
(1)求AB的长;
(2)求点C到直线AB的距离.
19.(2021秋 兴宁市期末)如图,某数学兴趣小组为测量一座古塔的高度,在古塔左侧的A点处测得古塔顶端D的仰角为30°,然后向古塔底端C前进30米到达点B处,测得古塔顶端D的仰角为45°,且点A、B、C在同一水平直线上,求古塔CD的高度.
20.(2021秋 房山区期末)如图,在△ABC中,AB=4,∠B=45°,∠C=60°.点E为线段AB的中点,点F是AC边上任一点,作点A关于线段EF的对称点P,连接AP,交EF于点M.连接EP,FP.当PF⊥AC时,求AP的长.
21.(2021秋 永定区期末)如图,一艘船正以海里/小时的速度向正东航行,在A处看小岛C在船北偏东60°,继续航行1小时到达B处,此时看见小岛C在船的北偏东30°.
(1)求小岛C到航线AB的距离.
(2)已知以小岛C为中心周围20海里内为我军导弹部队军事演习的着弹危险区,问这艘船继续向东航行,是否有进入危险区的可能?
22.(2021秋 龙口市期末)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
23.(2021秋 西湖区校级月考)阅读下列材料,并解决问题.
如图1,在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c,过点A作AD⊥BC于点D,则,,即AD=csinB,AD=bsinC.于是csinB=bsinC,即.同理有:,,所以.即在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
(1)如图2,一货轮在B处测得灯塔A在货轮的北偏东15°的方向上,随后货轮以80海里/时的速度向正东方向航行,半小时后到达C处,此时又测得灯塔A在货轮的北偏西30°的方向上,求此时货轮距灯塔A的距离AC.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)
答案与解析
一.选择题
1.(2021秋 泗水县期末)如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cosB的是( )
A. B. C. D.
【解析】解:A.∵CD⊥AB,
∴∠CDB=∠ADB=90°,
∴∠B+∠BCD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠B=∠ACD,
在Rt△ACD中,cos∠ACD=,
∴cosB=,
故A不符合题意;
B.在Rt△DBC中,cosB=,故B不符合题意;
C.在Rt△DBC中,cos∠BCD=,
∵∠A≠45°,
∴∠B≠45°,
∴∠B≠∠BCD,
∴cosB≠,
故C符合题意;
D.在Rt△ABC中,cosB=,故D不符合题意;
故选:C.
2.(2021秋 市北区期末)在Rt△ABC中,∠C=90°,已知∠A及边BC=a,则Rt△ABC的斜边长应为( )
A.asinA B. C.acosA D.
【解析】解:在Rt△ABC中,∠C=90°,已知∠A及边BC=a,
∴AB==,
∴Rt△ABC的斜边长应为:,
故选:B.
3.(2021秋 嘉定区期末)在△ABC中,AB=AC=10,,那么BC的长是( )
A.4 B.8 C. D.
【解析】解:过点A作AD⊥BC,垂足为D,
在Rt△ABD中,AB=10,,
∴BD=ABcosB=10×=4,
∵AB=AC,AD⊥BC,
∴BC=2BD=8,
故选:B.
4.(2021秋 拱墅区期末)如图,在平面直角坐标系内有一点P(3,4),连接OP,设OP与x轴正半轴所夹的锐角为α,则锐角α的正弦值为( )
A. B. C. D.
【解析】解:过点P作PA⊥x轴,垂足为A,
∵P(3,4),
∴OA=3,AP=4,
∴OP===5,
在Rt△OAP中,sinα==,
故选:B.
5.(2021秋 海口期末)一段拦水坝横断面如图所示,迎水坡AB的坡度为i=1:,坝高BC=6m,则坡面AB的长度( )
A.12m B.18m C.6 D.12
【解析】解:∵迎水坡AB的坡度为i=1:,坝高BC=6m,
∴
即
解得AC=6,
∴AB==m,
故选:A.
6.(2021秋 青岛期末)如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC=( )
A. B. C. D.
【解析】解:连接CD,
由图可得:CD⊥AB,
由题意得:CD==,
AC==2,
在Rt△ACD中,sin∠BAC===,
故选:D.
7.(2021秋 海口期末)如图,点A、B、C都在边长为1的正方形格点上,连接AB、BC,则cos∠ABC的值为( )
A. B. C. D.1
【解析】解:连接AC,
由题意得:
AB2=32+12=10,
AC2=12+32=10,
BC2=22+42=20,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,
∵AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∴cos∠ABC=,
故选:B.
8.(2021秋 河东区期末)如图,在△ABC中,∠A=120°,AB=2,AC=1,则sinB的值是( )
A. B. C. D.
【解析】解:过点C作CD⊥BA,交BA的延长线于点D,
∵∠BAC=120°,
∴∠CAD=180°﹣∠BAC=60°,
在Rt△CAD中,CD=ACsin60°=1×=,
AD=ACcos60°=1×=,
∵AB=2,
∴BD=AB+AD=2+=,
在Rt△BCD中,BC===,
∴sinB===,
故选:D.
9.(2021秋 湖州期末)如图,在Rt△ABC中,∠ACB=90°,AC=4,tanA=.以点C为圆心,CB长为半径的圆交AB于点D,则AD的长是( )
A.1 B. C. D.2
【解析】解:过点C作CE⊥AB,垂足为E,
在Rt△ABC中,∠ACB=90°,AC=4,tanA=,
∴,
∴BC=3,
∴AB===5,
∵△ABC的面积=AB CE=AC BC,
∴5CE=12,
∴CE=,
在Rt△BCE中,CE===,
∵CE⊥BD,
∴BD=2BE=,
∴AD=AB﹣BD=5﹣=,
故选:B.
10.(2020 肥城市四模)如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10 B.15 C.15 D.15﹣5
【解析】解:在Rt△CDE中,
∵CD=10m,DE=5m,
∴sin∠DCE=,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===10(m),
∴AB=BC sin60°=10×=15(m).
故选:B.
二.填空题
11.(2021秋 长春期末)如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,则sinB的值为 .
【解析】解:∵CD=6,tanA=,
∴tanA==,
∴AD=4,
∵AB=12,
∴BD=AB﹣AD=12﹣4=8,
由勾股定理可得BC===10,
∴sinB===,
故答案为:.
12.(2021秋 杨浦区期末)如图,海中有一个小岛A,一艘轮船由西向东航行,在点B处测得小岛A在它的北偏东60°方向上,航行12海里到达点C处,测得小岛A在它的北偏东30°方向上,那么小岛A到航线BC的距离等于 6 海里.
【解析】解:过点A作AE⊥BC交BC的延长线于点E,
由题意得:BC=12海里,∠ABC=90°﹣60°=30°,∠ACE=90°﹣30°=60°,
∴∠BAC=∠ACE﹣∠ABC=30°,
∴∠BAC=∠ABC,
∴AC=BC=12海里,
在Rt△ACE中,sin∠ACE=,
∴AE=AC sin∠ACE=12×=6(海里),
即小岛A到航线BC的距离是6海里,
故答案为:6.
13.(2021秋 普陀区期末)如图,在△ABC中,∠A=90°,斜边BC的垂直平分线分别交AB、BC交于点D、E,如果cosB=,AB=7,那么CD的长等于 .
【解析】解:在△ABC中,∠A=90°,cosB=,AB=7,
∴BC=AB÷cosB=7=8,
∵斜边BC的垂直平分线分别交AB、BC交于点D、E,
∴BE=BC=4,
∴CD=BD=BE÷cosB=4=,
故答案为:.
14.(2021秋 邵东市期末)如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向(点A、B、C在同一平面),则这段河的宽度为 米(结果保留根号)
【解析】解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x=30(+1),
答:这段河的宽约为30(+1)米.
故答案为:30(+1).
15.(2021秋 潜山市期末)如图,△ABC中,过点B作BD⊥AB,交AC于点D,且AD:CD=4:3,∠ABC=150°.
(1)BD:BC= 2:7 ;
(2)若AB=4,则△ABC的面积是 2 .
【解析】解:(1)过点C作CE⊥AB,交AB的延长线于点E,
∵∠ABC=150°,
∴∠CBE=180°﹣∠ABC=30°,
∴设CE为a,则BC为2a,
∵BD⊥AB,CE⊥AB,
∴∠ABD=∠AEC=90°,
∵∠A=∠A,
∴△ABD∽△AEC,
∴=,
∴=,
∴BD=a,
∴==,
故答案为:2:7;
(2)由(1)得:△ABD∽△AEC,
∴=,
∴=,
∴AE=7,
∴BE=AE﹣AB=7﹣4=3,
在Rt△BEC中,CE=BEtan30°=3×=,
∴△ABC的面积=AB CE=×4×=2,
故答案为:2.
16.(2021秋 海陵区期末)如图所示,在边长相同的小正方形组成的网格中,两条经过格点的线段相交所成的锐角为α,则cosα等于 .
【解析】解:如图:设AB与CD相交于点E,过点C作CF∥AB,连接DF,
∵AB∥CF,
∴∠AEC=∠DCF,
由勾股定理得:
DC2=12+32=10,
DF2=12+22=5,
CF2=12+22=5,
∴DF2+CF2=DC2,且CF=DF,
∴△DCF是等腰直角三角形,
∴∠DCF=45°,
∴α=45°,
∴cosα=,
故答案为:.
三.解答题
17.(2021秋 溧阳市期末)(1)在△ABC中,∠C=90°,∠A=60°,BC=8,求AB和AC的长;
(2)在△ABC中,∠C=90°,a=,b=3,解这个直角三角形.
【解析】解:(1)在△ABC中,∠C=90°,∠A=60°,BC=8,
∴AB===,
∴AC=ABcos60°=×=,
答:,;
(2)在△ABC中,∠C=90°,a=,b=3,
∴tanA===,
∴∠A=30°,
∴c=2a=2,
∴∠B=90°﹣∠A=60°,
∴,∠A=30°,∠B=60°.
18.(2021秋 青浦区期末)如图,在△ABC中,点D是BC的中点,联结AD,AB=AD,BD=4,tanC=.
(1)求AB的长;
(2)求点C到直线AB的距离.
【解析】解:(1)∵过点A作AH⊥BD,垂足为点H.
∵AB=AD,
∴BH=HD=BD=2.
∵点D是BC的中点,
∴BD=CD=4.
∴HC=HD+CD=6.
∵=,
∴.
∵
=
=.
(2)过点C作CG⊥BA,交BA的延长线于点G.
∵,
∴.
∴.
∴点C到直线AB的距离为.
19.(2021秋 兴宁市期末)如图,某数学兴趣小组为测量一座古塔的高度,在古塔左侧的A点处测得古塔顶端D的仰角为30°,然后向古塔底端C前进30米到达点B处,测得古塔顶端D的仰角为45°,且点A、B、C在同一水平直线上,求古塔CD的高度.
【解析】解:由题意可知,AB=30,∠C=90°,∠A=30°,∠DBC=45°,
在Rt△BCD中,∠BDC=180°﹣90°﹣∠DBC=45°=∠DBC,
∴BC=CD.
设CD=x米,则BC=x米,AC=(30+x)米,
在Rt△ACD中,
tan30°=.
解得x=15+15,
答:古塔CD的高度为(15+15)米.
20.(2021秋 房山区期末)如图,在△ABC中,AB=4,∠B=45°,∠C=60°.点E为线段AB的中点,点F是AC边上任一点,作点A关于线段EF的对称点P,连接AP,交EF于点M.连接EP,FP.当PF⊥AC时,求AP的长.
【解析】解:如图1中,过点A作AD⊥BC于D.
在Rt△ABD中,AD=AB sin45°=4×=4.
如图2中,AC===,
∵PF⊥AC,
∴∠PFA=90°,
∵沿EF将△AEF折叠得到△PEF.
∴△AEF≌△PEF,
∴∠AFE=∠PFE=45°,AF=PF,
∴∠AFE=∠B,
∵∠EAF=∠CAB,
∴△AEF∽△ACB,
∴=,即=,
∴AF=2,
∴AP=AF=2.
21.(2021秋 永定区期末)如图,一艘船正以海里/小时的速度向正东航行,在A处看小岛C在船北偏东60°,继续航行1小时到达B处,此时看见小岛C在船的北偏东30°.
(1)求小岛C到航线AB的距离.
(2)已知以小岛C为中心周围20海里内为我军导弹部队军事演习的着弹危险区,问这艘船继续向东航行,是否有进入危险区的可能?
【解析】解:(1)作CD⊥AB交AB于点D,
由题意可知:∠CAB=90°﹣60°=30°,∠CBD=90°﹣30°=60°,
∴∠ACB=∠CBD﹣∠CAB=30°,
∴∠CAB=∠ACB,
∴AB=CB=×=,
在Rt△CBD中,CD=CB×sin∠CBD=×=16,
∴小岛C到航线AB的距离为16海里;
(2)∵CD=16<20,
∴这艘船继续向东航行会有进入危险区的可能.
22.(2021秋 龙口市期末)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
【解析】解:(1)在Rt△ABE中,AB=26,i==,
设BE=12k,AE=5k,则AB=13k=26,k=2,
∴AE=10(米),BE=24(米);
(2)过点F作FG⊥AD于点G,
由题意可知:FG=BE=24,∠FAD=53°,
在Rt△AFG中,cot53°==0.75,
∴AG=18(米),
∴BF=GE=AG﹣AE=8(米),
答:改造前坡顶与地面的距离BE为24米;BF至少是8米.
23.(2021秋 西湖区校级月考)阅读下列材料,并解决问题.
如图1,在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c,过点A作AD⊥BC于点D,则,,即AD=csinB,AD=bsinC.于是csinB=bsinC,即.同理有:,,所以.即在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
(1)如图2,一货轮在B处测得灯塔A在货轮的北偏东15°的方向上,随后货轮以80海里/时的速度向正东方向航行,半小时后到达C处,此时又测得灯塔A在货轮的北偏西30°的方向上,求此时货轮距灯塔A的距离AC.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)
【解析】解:(1)由示意图可知:∠ACB=60°,
由平行线的性质可知∠ABC=180°﹣30°﹣60°﹣15°=75°,
则∠A=180°﹣∠C﹣∠B=45°,BC=80×=40(海里),
过B作BD⊥AC于点D,
则∠BDC=90°,∠DBC=30°,
∴DC=BC=20(海里),
由勾股定理得:BD==20(海里),
∵∠A=45°,∠ADB=90°,
∴∠ABD=∠A=45°,
∴AD=BD=20海里,
∴AC=AD+CD=(20+20)(海里),
答:此时货轮距灯塔A的距离AC为(20+20)海里;
(2)如图,由(1)知,CD=20海里,BD==20海里,AD=BD=20海里,
∴AC=AD+CD=(20+20)海里,
∵=,
∴=,
∴sin75°=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
