苏科版·数学 九年级下册 6.4 探索三角形相似的条件 教案(表格式)
文档属性
| 名称 | 苏科版·数学 九年级下册 6.4 探索三角形相似的条件 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 222.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 15:09:52 | ||
图片预览

文档简介
数学教学设计
教 材:苏科版·数学(九年级下册)
6.4 探索三角形相似的条件(1)
教学目标 1.掌握平行线分线段成比例定理及其推论,学会灵活应用;2.经历“操作——观察——探索——说理”的数学活动过程,发展合情推理和有条理的表达能力.
教学重点 探索“见平行,得相似”的相关结论.
教学难点 成比例的线段中对应线段的确定.
教学过程(教师) 学生活动 设计思路
温故知新1、由得(比例的合比性)2、相似三角形的定义:三角对应相等,三边对应成比例的三角形叫相似三角形 积极思考,口头回答 为新知识的引入作准备
作图活动活动一:在作业本(单线抄)上任意画一条直线与一组平行线都相交,相邻交点间的线段相等吗?再画一条试试。尝试添加辅助线并口头证明。 画图,观察,猜想,交流,讨论,最后得出添加辅助线方法并口头证明 活动引入,激发学生的探究兴趣.
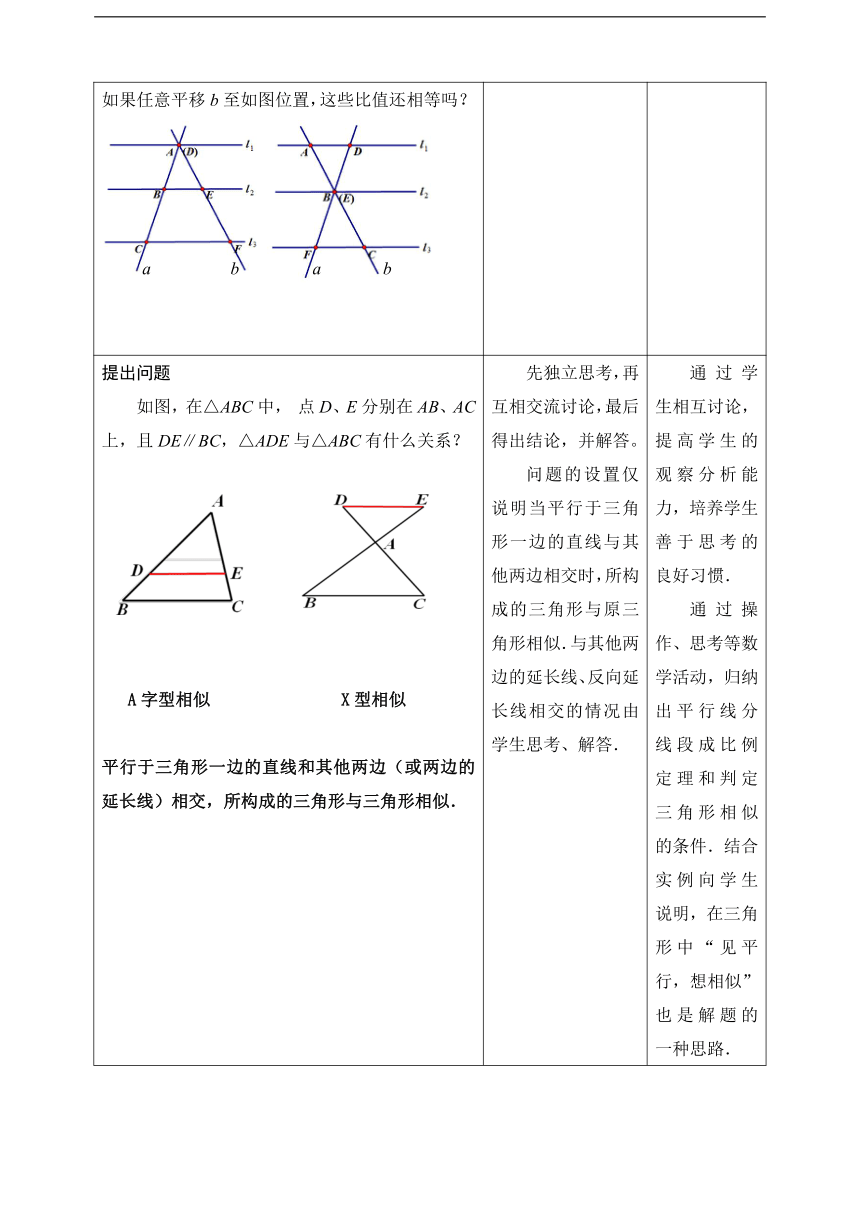
探索新知活动二:如图,画三条互相平行的直线l1、l2、l3,再任意画2条直线a、b,使 a、b分别与l1、l2、l3相交于点A、B、C和点D、E、F.与相等吗?如果相等,你还能得到其它的成比例线段吗?如果任意平移b至如图位置,这些比值还相等吗? 组织学生积极操作与思考,利用小组合作的方式进行,最后归纳得出结论:两条直线被一组平行线所截,所得的对应线段成比例. 活动引入,激发学生的探究兴趣.通过学生相互讨论,提高学生的观察分析能力,培养学生善于思考的良好习惯.
提出问题如图,在△ABC中, 点D、E分别在AB、AC上,且DE∥BC,△ADE与△ABC有什么关系? A字型相似 X型相似平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似. 先独立思考,再互相交流讨论,最后得出结论,并解答。问题的设置仅说明当平行于三角形一边的直线与其他两边相交时,所构成的三角形与原三角形相似.与其他两边的延长线、反向延长线相交的情况由学生思考、解答. 通过学生相互讨论,提高学生的观察分析能力,培养学生善于思考的良好习惯.通过操作、思考等数学活动,归纳出平行线分线段成比例定理和判定三角形相似的条件.结合实例向学生说明,在三角形中“见平行,想相似”也是解题的一种思路.
尝试交流1.如果再作MN∥DE,共有多少对相似三角形? 2.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来. 先由学生独立思考;再小组交流讨论,并得出合理解答。 设计尝试交流的目的是为了加深学生对相似判定方法(1)的理解,同时为后续学习作好铺垫.题1也可以向学生介绍相似三角形的传递性.
拓展延伸3、如图,在△ABC中,DG∥EH∥FI∥BC.(1)请找出图中所有的相似三角形;(2)如果AD=1,DB=3,那么DG∶BC=_____.4、如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.5、如图所示,点D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB . 先由学生独立思考;再小组交流讨论,并得出合理解答。 设计拓展延伸的目的是为了进一步加深学生平行线分线段成比例定理的理解,同时培养学生分析问题、解决问题的能力.
课堂小结通过这节课的学习,你学习到什么新知识?获得了什么经验?还有什么疑问?1、平行线分线段成比例;2、见平行,得相似 学生讨论小结本节课内容. 培养学生反思自己学习过程的意识,充分发挥学生的主体作用,从而培养归纳、整理、表达的能力.
课后作业1.必做题:课本54-55页练习第1、2题; 课本习题6.4第1、3、7题.2.选做题:课本习题6.4第2、4题.3.小练习 学生独立完成. 布置课后作业的主要目的是巩固本节课所学知识.
a
b
b
a
a
b
教 材:苏科版·数学(九年级下册)
6.4 探索三角形相似的条件(1)
教学目标 1.掌握平行线分线段成比例定理及其推论,学会灵活应用;2.经历“操作——观察——探索——说理”的数学活动过程,发展合情推理和有条理的表达能力.
教学重点 探索“见平行,得相似”的相关结论.
教学难点 成比例的线段中对应线段的确定.
教学过程(教师) 学生活动 设计思路
温故知新1、由得(比例的合比性)2、相似三角形的定义:三角对应相等,三边对应成比例的三角形叫相似三角形 积极思考,口头回答 为新知识的引入作准备
作图活动活动一:在作业本(单线抄)上任意画一条直线与一组平行线都相交,相邻交点间的线段相等吗?再画一条试试。尝试添加辅助线并口头证明。 画图,观察,猜想,交流,讨论,最后得出添加辅助线方法并口头证明 活动引入,激发学生的探究兴趣.
探索新知活动二:如图,画三条互相平行的直线l1、l2、l3,再任意画2条直线a、b,使 a、b分别与l1、l2、l3相交于点A、B、C和点D、E、F.与相等吗?如果相等,你还能得到其它的成比例线段吗?如果任意平移b至如图位置,这些比值还相等吗? 组织学生积极操作与思考,利用小组合作的方式进行,最后归纳得出结论:两条直线被一组平行线所截,所得的对应线段成比例. 活动引入,激发学生的探究兴趣.通过学生相互讨论,提高学生的观察分析能力,培养学生善于思考的良好习惯.
提出问题如图,在△ABC中, 点D、E分别在AB、AC上,且DE∥BC,△ADE与△ABC有什么关系? A字型相似 X型相似平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似. 先独立思考,再互相交流讨论,最后得出结论,并解答。问题的设置仅说明当平行于三角形一边的直线与其他两边相交时,所构成的三角形与原三角形相似.与其他两边的延长线、反向延长线相交的情况由学生思考、解答. 通过学生相互讨论,提高学生的观察分析能力,培养学生善于思考的良好习惯.通过操作、思考等数学活动,归纳出平行线分线段成比例定理和判定三角形相似的条件.结合实例向学生说明,在三角形中“见平行,想相似”也是解题的一种思路.
尝试交流1.如果再作MN∥DE,共有多少对相似三角形? 2.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来. 先由学生独立思考;再小组交流讨论,并得出合理解答。 设计尝试交流的目的是为了加深学生对相似判定方法(1)的理解,同时为后续学习作好铺垫.题1也可以向学生介绍相似三角形的传递性.
拓展延伸3、如图,在△ABC中,DG∥EH∥FI∥BC.(1)请找出图中所有的相似三角形;(2)如果AD=1,DB=3,那么DG∶BC=_____.4、如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.5、如图所示,点D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB . 先由学生独立思考;再小组交流讨论,并得出合理解答。 设计拓展延伸的目的是为了进一步加深学生平行线分线段成比例定理的理解,同时培养学生分析问题、解决问题的能力.
课堂小结通过这节课的学习,你学习到什么新知识?获得了什么经验?还有什么疑问?1、平行线分线段成比例;2、见平行,得相似 学生讨论小结本节课内容. 培养学生反思自己学习过程的意识,充分发挥学生的主体作用,从而培养归纳、整理、表达的能力.
课后作业1.必做题:课本54-55页练习第1、2题; 课本习题6.4第1、3、7题.2.选做题:课本习题6.4第2、4题.3.小练习 学生独立完成. 布置课后作业的主要目的是巩固本节课所学知识.
a
b
b
a
a
b
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
