人教版九年级下册数学同步课时作业26.2 第1课时 反比例函数的实际应用(含答案)
文档属性
| 名称 | 人教版九年级下册数学同步课时作业26.2 第1课时 反比例函数的实际应用(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 12:02:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学同步课时作业
第二十六章 反比例函数
26.2 实际问题与反比例函数
第1课时 反比例函数的实际应用
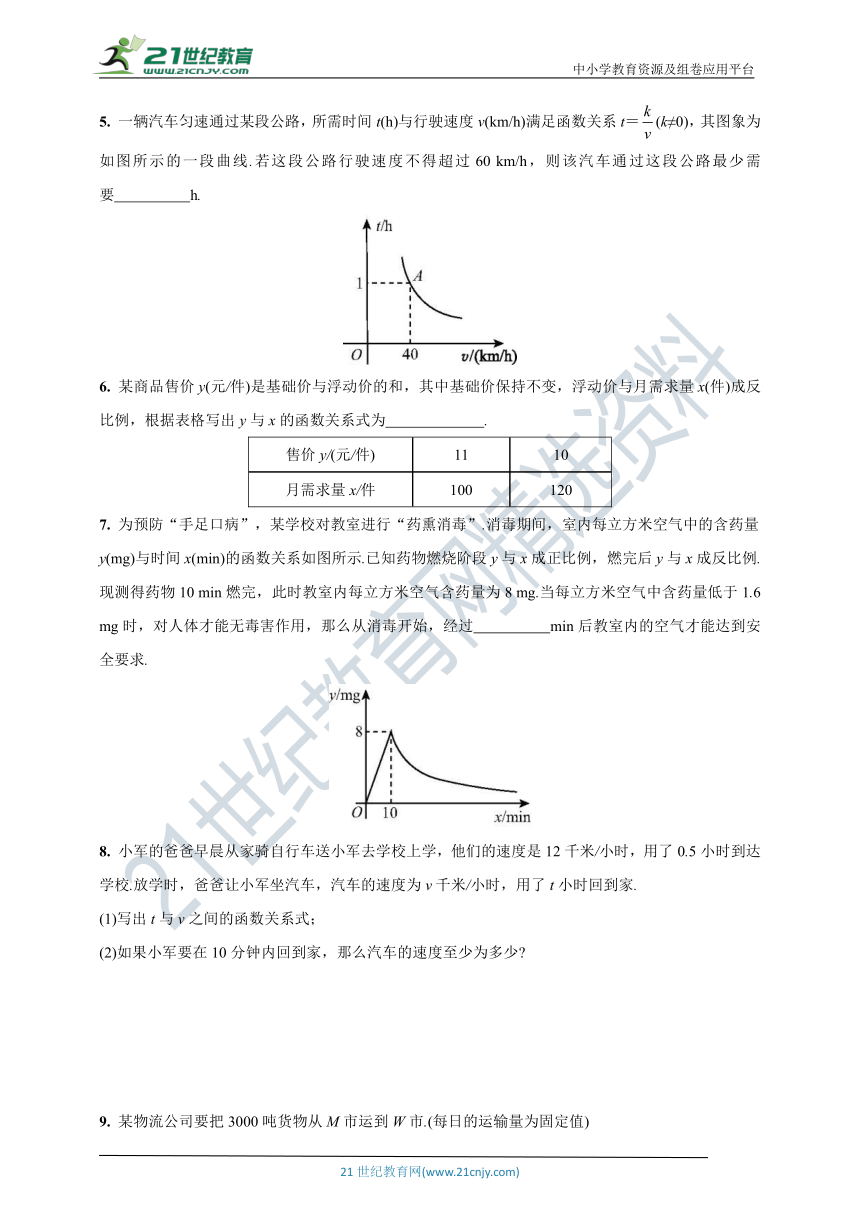
1. 菱形的面积为2,其对角线长分别为x,y,则y与x的图象大致为( )
A B C D
2. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系.当x=2时,y=10,则y与x的函数图象大致是( )
A B C D
3. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是双曲线y=(k≠0)的一部分,则当x=16时,大棚内的温度约为( )
A.18 ℃ B.15.5 ℃ C.13.5 ℃ D.12 ℃
4. 把一个长、宽、高分别为3 cm,2 cm,1 cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为 .
5. 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系t=(k≠0),其图象为如图所示的一段曲线.若这段公路行驶速度不得超过60 km/h,则该汽车通过这段公路最少需要 h.
6. 某商品售价y(元/件)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比例,根据表格写出y与x的函数关系式为 .
售价y/(元/件) 11 10
月需求量x/件 100 120
7. 为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(min)的函数关系如图所示.已知药物燃烧阶段y与x成正比例,燃完后y与x成反比例.现测得药物10 min燃完,此时教室内每立方米空气含药量为8 mg.当每立方米空气中含药量低于1.6 mg时,对人体才能无毒害作用,那么从消毒开始,经过 min后教室内的空气才能达到安全要求.
8. 小军的爸爸早晨从家骑自行车送小军去学校上学,他们的速度是12千米/小时,用了0.5小时到达学校.放学时,爸爸让小军坐汽车,汽车的速度为v千米/小时,用了t小时回到家.
(1)写出t与v之间的函数关系式;
(2)如果小军要在10分钟内回到家,那么汽车的速度至少为多少
9. 某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(吨)与运输时间x(天)之间有怎样的函数关系式
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务.求原计划完成运输任务的天数.
10. 如图,学校打算用某种材料围建一个面积为18平方米的矩形ABCD生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米.设AD的长为y米,CD的长为x米.
(1)求y与x之间的函数解析式;
(2)若围成矩形ABCD生物园的三边材料总长不超过18米,且AD和CD的长度都是整数,试求出满足条件的所有围建方案.
11. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10 ℃,加热到100 ℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30 ℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30 ℃时接通电源,水温y(℃)与时间x(min)的关系如图所示:
(1)分别写出水温上升和下降阶段y与x之间的函数关系式;
(2)怡萱同学想喝高于50 ℃的水,请问她最多需要等待多长时间
12. 如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.实验表明:点M与点A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且当t=1时,h=5,点M与点A的水平距离是vt米.(忽略空气阻力)
(1)求k的值,并用t表示h.
(2)设v=5,用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离.
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
参 考 答 案
1. C 2. D 3. C
4. S=
5.
6. y=+5
7. 50
8. 解:(1)t与v之间的函数关系式为t=.
(2)10分钟=小时,当t=时,v=6÷=36.答:汽车的速度至少为36千米/小时.
9. 解:(1)由题意得xy=3000,∴y=(x>0).
(2)设原计划x天完成运输任务.根据题意,得(1-20%)=,解得x=4.经检验x=4是原方程的根.答:原计划4天完成运输任务.
10. 解:(1)根据题意,得xy=18,∴y=(0(2)由题意可知且y=,∴符合条件的有当x=3时,y=6;当x=6时,y=3.答:满足条件的所有围建方案为AD=6米,CD=3米或AD=3米,CD=6米.
11. 解:(1)由题意可得y与x的函数关系式为y=且这个过程每min循环一次.
(2)将y=50代入y=10x+30,解得x=2;将y=50代入y=,解得x=14.∵-14=(min),+2=(min),∴怡萱同学想喝高于50 ℃的水,她最多需要等待 min.
12. 解:(1)由题意,将点A(1,18)代入y=,得18=,∴k=18.设h=at2,把t=1,h=5代入,得a=5,∴h=5t2.
(2)∵v=5,AB=1,∴x=5t+1.∵h=5t2,OB=18,∴y=-5t2+18.由x=5t+1,得t=(x-1),∴y=-(x-1)2+18=-x2+x+,当y=13时,解得x=6或-4.又∵x≥1,∴x=6.把x=6代入y=,得y=3,∴当y=13时,运动员与正下方滑道的竖直距离是13-3=10(米).
(3)把y=1.8代入y=-5t2+18,得t2=,解得t=1.8或-1.8(负值舍去),∴x=10,∴甲的坐标(10,1.8)恰好落在滑道y=上,此时乙的坐标为(1+1.8v乙,1.8),由题意可知1+1.8v乙-(1+5×1.8)>4.5,∴v乙>7.5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学同步课时作业
第二十六章 反比例函数
26.2 实际问题与反比例函数
第1课时 反比例函数的实际应用
1. 菱形的面积为2,其对角线长分别为x,y,则y与x的图象大致为( )
A B C D
2. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系.当x=2时,y=10,则y与x的函数图象大致是( )
A B C D
3. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是双曲线y=(k≠0)的一部分,则当x=16时,大棚内的温度约为( )
A.18 ℃ B.15.5 ℃ C.13.5 ℃ D.12 ℃
4. 把一个长、宽、高分别为3 cm,2 cm,1 cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为 .
5. 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系t=(k≠0),其图象为如图所示的一段曲线.若这段公路行驶速度不得超过60 km/h,则该汽车通过这段公路最少需要 h.
6. 某商品售价y(元/件)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比例,根据表格写出y与x的函数关系式为 .
售价y/(元/件) 11 10
月需求量x/件 100 120
7. 为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(min)的函数关系如图所示.已知药物燃烧阶段y与x成正比例,燃完后y与x成反比例.现测得药物10 min燃完,此时教室内每立方米空气含药量为8 mg.当每立方米空气中含药量低于1.6 mg时,对人体才能无毒害作用,那么从消毒开始,经过 min后教室内的空气才能达到安全要求.
8. 小军的爸爸早晨从家骑自行车送小军去学校上学,他们的速度是12千米/小时,用了0.5小时到达学校.放学时,爸爸让小军坐汽车,汽车的速度为v千米/小时,用了t小时回到家.
(1)写出t与v之间的函数关系式;
(2)如果小军要在10分钟内回到家,那么汽车的速度至少为多少
9. 某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(吨)与运输时间x(天)之间有怎样的函数关系式
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务.求原计划完成运输任务的天数.
10. 如图,学校打算用某种材料围建一个面积为18平方米的矩形ABCD生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米.设AD的长为y米,CD的长为x米.
(1)求y与x之间的函数解析式;
(2)若围成矩形ABCD生物园的三边材料总长不超过18米,且AD和CD的长度都是整数,试求出满足条件的所有围建方案.
11. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10 ℃,加热到100 ℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30 ℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30 ℃时接通电源,水温y(℃)与时间x(min)的关系如图所示:
(1)分别写出水温上升和下降阶段y与x之间的函数关系式;
(2)怡萱同学想喝高于50 ℃的水,请问她最多需要等待多长时间
12. 如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.实验表明:点M与点A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且当t=1时,h=5,点M与点A的水平距离是vt米.(忽略空气阻力)
(1)求k的值,并用t表示h.
(2)设v=5,用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离.
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
参 考 答 案
1. C 2. D 3. C
4. S=
5.
6. y=+5
7. 50
8. 解:(1)t与v之间的函数关系式为t=.
(2)10分钟=小时,当t=时,v=6÷=36.答:汽车的速度至少为36千米/小时.
9. 解:(1)由题意得xy=3000,∴y=(x>0).
(2)设原计划x天完成运输任务.根据题意,得(1-20%)=,解得x=4.经检验x=4是原方程的根.答:原计划4天完成运输任务.
10. 解:(1)根据题意,得xy=18,∴y=(0
11. 解:(1)由题意可得y与x的函数关系式为y=且这个过程每min循环一次.
(2)将y=50代入y=10x+30,解得x=2;将y=50代入y=,解得x=14.∵-14=(min),+2=(min),∴怡萱同学想喝高于50 ℃的水,她最多需要等待 min.
12. 解:(1)由题意,将点A(1,18)代入y=,得18=,∴k=18.设h=at2,把t=1,h=5代入,得a=5,∴h=5t2.
(2)∵v=5,AB=1,∴x=5t+1.∵h=5t2,OB=18,∴y=-5t2+18.由x=5t+1,得t=(x-1),∴y=-(x-1)2+18=-x2+x+,当y=13时,解得x=6或-4.又∵x≥1,∴x=6.把x=6代入y=,得y=3,∴当y=13时,运动员与正下方滑道的竖直距离是13-3=10(米).
(3)把y=1.8代入y=-5t2+18,得t2=,解得t=1.8或-1.8(负值舍去),∴x=10,∴甲的坐标(10,1.8)恰好落在滑道y=上,此时乙的坐标为(1+1.8v乙,1.8),由题意可知1+1.8v乙-(1+5×1.8)>4.5,∴v乙>7.5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
